
Title: Account of the Skerryvore lighthouse
with notes on the illumination of lighthouses
Author: Alan Stevenson
Release date: January 26, 2025 [eBook #75213]
Language: English
Original publication: Edinburgh: Adam and Charles Black, 1848
Credits: deaurider, Harry Lamé and the Online Distributed Proofreading Team at https://www.pgdp.net (This file was produced from images generously made available by The Internet Archive)
Please see the Transcriber’s Notes at the end of this text.
Larger versions of illustrations and plates are available by opening them in a new tab or window.
New original cover art included with this eBook is granted to the public domain.


SKERRYVORE LIGHTHOUSE.
BY
ALAN STEVENSON, LL.B., F.R.S.E., M.I.C.E.,
ENGINEER TO THE NORTHERN LIGHTHOUSE BOARD.

“ΥΠΕΡ · ΤΩΝ · ΠΛΩΙΖΟΜΕΝΩΝ”
Inscription on the Ancient Pharos of Alexandria.
BY ORDER OF THE COMMISSIONERS OF NORTHERN LIGHTHOUSES.
ADAM AND CHARLES BLACK, NORTH BRIDGE, EDINBURGH.
LONGMAN AND CO., LONDON.
MDCCCXLVIII.
PRINTED BY NEILL AND COMPANY, EDINBURGH.
[iii]
I am unwilling to dismiss the following pages from my hands without saying a few words in extenuation of the defects which they contain. My chief plea in defence is, that the preparation of this Account of the Skerryvore Lighthouse, and the Notes on the Illumination of Lighthouses which follow it, was not chosen or assumed by me, but was a task imposed by the express desire of the Lighthouse Board, to whose enlightened and liberal views the Mariner owes the erection of the Lighthouse itself. My labours were also continually interrupted by the urgent calls of my official duties; and, on several occasions, I was forced to dismiss unfinished chapters from my mind for a period of several months—circumstances which, I hope, will in some measure account for the desultory character of the performance, the disproportion of some of its parts, and more especially for repetitions and perhaps omissions which would otherwise have been quite unpardonable.
Having said thus much by way of apology for this Volume, I must acknowledge my many and great obligations to my Father who preceded me as Engineer to the Board of Northern Lighthouses, and of whose experience, as the Architect of no fewer than twenty-five Lighthouses, including that of the Bell Rock, I had[iv] the full benefit during the erection of the Skerryvore Lighthouse. To the generosity of my esteemed friend, M. Leonor Fresnel, I owe all that I know of the Dioptric System of Illumination, invented by his late illustrious Brother; but this general acknowledgment will not supersede the necessity of frequent repetitions of my obligations to him, as occasion offers, in the course of these pages. I have also derived much assistance, as a careful reader will easily trace, from the valuable little work of M. Peclet, entitled Traité de l’Eclairage. There are, besides, many other obligations, which I cannot attempt to acknowledge individually, but which those, who kindly conferred them, well know how much I value.
In the Account of the Skerryvore Lighthouse, which forms the first part of this Volume, there is an important omission; and, in this short prefatory notice, I gladly embrace the only opportunity, which now remains, of supplying the defect. Although, in the course of the Narrative, I have occasionally noticed some special deliverances from danger, I have altogether neglected to record the remarkable fact, that, amidst our almost daily perils, during six seasons on the Skerryvore Rock, there was no loss of either life or limb amongst us. Those who best know the nature of the service in which we were engaged,—the daily jeopardy connected with landing weighty materials in a heavy surf and transporting the workmen in boats through a boisterous sea, the risks to so many men, involved in mining the foundations of the Tower in a space so limited, and above all, the destruction, in a single night by the violence of the waves, of our temporary barrack on the Rock,[v] which had cost the toils of a whole season, will not wonder that I am anxious to express, what I know to have been a general feeling amongst those engaged in the work—that of heartfelt thankfulness to Almighty God for merciful preservation in danger, and for the final success which terminated our arduous and protracted labours.
Edinburgh, March 25, 1848.
| PART I. | |
| ACCOUNT OF SKERRYVORE LIGHTHOUSE. | |
| Page | |
| Introduction — Constitution of the Lighthouse Board — Lights established since 1821 — Improvements in the mode of illumination — Dioptric Lights — Beacons and Buoys, | 9 |
| CHAPTER I. | |
| Topographic notice of the Skerryvore Rock, | 19 |
| CHAPTER II. | |
| Preliminary arrangements and works, including survey of the rocks, and opening of quarries from 1834 to 1837 — Survey of the Skerryvore rocks — Disadvantages of Tyree — Pier and workyard at Hynish, Tyree — Quarries at Hynish — Skerryvore Committee appointed, | 37 |
| CHAPTER III. | |
| On the construction of Lighthouse Towers, | 45 |
| CHAPTER IV. OPERATIONS OF 1838. |
|
| Temporary Barrack on Rock — Tools and machinery — Steam Tender for the works — Employment and wages of workmen — Progress of the outfit for the season’s operations — Embark for Skerryvore — Lay down moorings, and try to land on the Rock — Driven to Mull — First day’s work on the Rock — Shipment of materials at Glasgow and Greenock — Reach Tyree — Driven to Mull — Return to Tyree — First good day’s work on the Rock — Sudden gale and great peril to the vessels — Reach Hynish in safety — Detained by bad weather four days at Hynish — Return to the Rock and have six days of good weather — Erection of the pyramid of the wooden barrack — Mode of determining the length of the beams, and the sites for their fixtures — Pyramid completed — Mode of living while erecting the barrack — Shoals of Medusæ seen — Driven by a gale to Mull — Return to Hynish and are driven to Coll — Return to the Rock — Driven to Tyree — Return to the Rock — Horizontal braces fixed — Driven to Mull — Heavy gale — Timber[viii] cast on Tyree — Return to Rock and further progress of barrack — Last day’s work on Rock this season — Precaution for the benefit of shipwrecked seamen — View from top of pyramid — Destruction of the barrack during a gale — Letter from Mr Hogben — Proceed to Skerryvore — State in which the Rock was found — Cause of the destruction of the barrack — Preparations for a new barrack — Works at Hynish — Hynish quarries, | 71 |
| CHAPTER V. OPERATIONS OF 1839. |
|
| Shipping station and pier at Hynish — Granite quarries in Mull — Observations on the quarrying of granite — Dressing of the Lighthouse blocks — Excavation of foundation for the Lighthouse Tower on the Skerryvore Rock — Fitting up of the second barrack on the Rock — Sudden death of George Middlemiss — Wharf and landing-place on the Rock — Ring-bolts, water-tanks, and railways — Incidents of the season — Effects of a gale from the south-west — Mutiny of the crew — Near approach of the vessels to the Rock, and other circumstances shewing the importance of a Light on the Skerryvore, | 107 |
| CHAPTER VI. OPERATIONS OF 1840. |
|
| Hynish workyard — Hynish pier — The Rock — Life in the barrack — Foundation-pit — Landing of the materials on the Rock — Laying the first stone, | 140 |
| CHAPTER VII. OPERATIONS OF 1841. |
|
| Hynish workyard — The Rock — The waves — Colours of the breaking waves — The seals, | 151 |
| CHAPTER VIII. OPERATIONS OF 1842. |
|
| State of the Rock in Spring of 1842 — Commencement of Rock operations — Last stone — The Lantern, | 163 |
| CHAPTER IX. CONCLUDING OPERATIONS AND EXHIBITION OF THE LIGHT. |
|
| Harbour works — Bo Pheg beacon — Light-keepers’ and seamen’s houses — Concluding works on the Rock, such as pointing, &c. — Interior fittings of the Tower — Light-room apparatus, and first exhibition of the Light — Removal of the barrack from the Rock — Expense, | 169[ix] |
| PART II. | |
| NOTES ON THE ILLUMINATION OF LIGHTHOUSES, WITH SHORT NOTICES OF THEIR HISTORY, 181. | |
| Early history, 181 — Colossus of Rhodes, 182 — Pharos of Alexandria, 183 — Coruna Tower, 187 — Lighthouse at the mouth of the Quadalquivir, 188 — Ancient Phari in Britain, 188 — Tour de Corduan, 189 — Eddystone, 189 — Bell Rock, 192 — Carlingford, 194 — Iron lighthouses, 194 — Early modes of illumination, 195 — Flame, 196 — Drummond and Voltaic Lights, 199 — Mr Gurney’s Lamp, 200 — Argand Burners, 200. | |
| CATOPTRIC SYSTEM OF LIGHTS, 204. | |
| Application of Paraboloidal Mirrors, 205 — Reflection, 207 — Paraboloidal Mirrors, 209 — Divergence of Paraboloidal Mirrors, 212 — Effect of Paraboloidal Mirrors, 217 — Power of ditto, 218 — Manufacture of reflectors, 218 — Testing of mirrors, 219 — Argand Lamps used in reflectors, 220 — Arrangements for raising or lowering the Argand wick, 222 — Flowing of the lamp, 223 — Placing the lamp in the focus, 226 — Distinctions of Catoptric Lights, 227 — Colour as a distinction for lights, 229 — Arrangement of reflectors on the frame, 230 — Bordier Marcet’s reflectors, 232 — Fanal sidéral, 232 — Fanal à double effet, 234 — Fanal à double face, 236 — Mr Barlow’s spherical mirrors, 237 — Captain Smith’s mirrors in the form of a parabolic spindle, 238. | |
| DIOPTRIC SYSTEM OF LIGHTS, 239. | |
| Early history of Lighthouse lenses, Condorcet, Buffon, Brewster, Fresnel, 239 — Refraction, 242 — Lenses, 245 — Spherical aberration, 248 — Fresnel’s formulæ for annular lenses, 249 — Testing lenses, 255 — Divergence of lenses, 256 — Illuminating power of lenses, 257 — Arrangement of lenses in a Lighthouse, 258 — Pyramidal lenses and mirrors, 259 — Curved mirrors, 260 — Cylindric refractors of fixed Lights, 263 — Application of crossed prisms to cause flashes, 264 — True cylindric form given to refractors, and other improvements in their construction, 264 — Catadioptric zones, the mode of computing their elements, &c., 267 — Testing of zones, 282 — Framing of zones, 286 — Mechanical lamp, 286 — Height of flame of mechanical lamp, 289 — Position of flame in reference to focus, 290 — Working of the pumps, 291 — Choice of focal point for various parts of apparatus, 292 — Choice of a focal point for zones, 292 — Application of spherical mirrors to fixed Dioptric Lights, 293 — Arrangement of Dioptric apparatus, 293 — Arrangement of Dioptric apparatus in Lightroom, 294 — Power of Dioptric instruments, 298 — Orders of French Lights, 298 — Distinctions of Dioptric Lights, 299 — Comparison of Dioptric and Catoptric apparatus for revolving lights, 301 — Comparison for fixed lights, 303 — Summary[x] of views as to two systems for revolving lights, 306 — Summary of views as to two systems for fixed lights, 306 — Advantages and disadvantages of both systems under certain circumstances, 308 — Distinctions of the Dioptric Lights and the application of coloured media, 311 — Captain Basil Hall’s proposal for fixed lights, 313 — Effects of rapid motion on the power of lights, 315 — Connection of experiments with irradiation, 320. | |
| VARIOUS GENERAL CONSIDERATIONS CONNECTED WITH LIGHTHOUSES, 320. | |
| Masking Lights, 320 — Double Lights, 322 — Leading Lights, 323 — Distribution of Lights on a coast, 325 — Height of Lighthouse Tower, and its relation to range of light, 328 — Diagonal Lantern, 330 — Glazing of Lantern, 331 — Ventilation of Lanterns, 331 — Arrangements and Management of a Lighthouse, 334 — Cleansing of apparatus, 335 — Mode of measuring relative power of lights, 336 — More accurate comparison of intensity of lights, 338 — Floating Lights, 346 — Beacons and Buoys, 347. | |
| 1. | Table of Co-ordinates of Hyperbolic Column. |
| 2. | Notes on the Making of Paraboloïdal Mirrors. |
| 3. | Notes on the Grinding and Polishing of Dioptric Instruments for Lighthouses. |
| 4. | Table of the Elements of the Catadioptric Zones for Lights of the first order in the system of Augustin Fresnel. |
| 5. | Notice to Mariners of the Exhibition of the Skerryvore Light. |
| 6. | Detailed Account of the Expense of the Skerryvore Lighthouse. |
| 7. | Excerpts from Account of Experiments on the Force of the Waves of the Atlantic and German Oceans, by Thomas Stevenson, F.R.S.E., Civil Engineer. |
| 8. | Annual List for 1848 of Lighthouses, Beacons, and Buoys, in the District of the Northern Lights Board. |
| 9. | Annual Report by the Secretary as to the Income and Expenditure of the Northern Lights Board for 1846. |
| 10. | Instructions to the Light-keepers in the Service of the Commissioners of the Northern Lighthouses. |
| I. | Chart shewing the situation of the Skerryvore Lighthouse. |
| II. | Chart shewing the position of the Skerryvore Rocks and foul ground. |
| III. | Plans of the Skerryvore Rock at high and low water of spring tides. |
| IV. | Curves for Lighthouse Towers — Marine Dynamometer. |
| V. | Barrack of timber on the Skerryvore Rock. |
| VI. | Details of fixtures of timbers at the top of the Timber Barrack. |
| VII. | Elevation of Skerryvore Lighthouse. |
| VIII. | Section of Skerryvore Lighthouse. |
| IX. | Balance Crane used at Skerryvore. |
| X. | Plan shewing the Lighthouse Establishment of Barracks, Harbour, &c., at Hynish, in the Island of Tyree. |
| XI. | Elevation and Section entrance to Dock at Hynish. |
| XII. | Plan and Section of Annular Lens. |
| XIII. | Perspective Elevation of Revolving Dioptric Apparatus of First Order. |
| XIV. | Plan of Revolving Dioptric Light of First Order, with Mirrors. |
| XV. | Vertical Section of fixed Dioptric Lights of First Order, with Mirrors. |
| XVI. | Elements of Concave Mirrors for Dioptric Lights of First Order, and arrangement on the Frame. |
| XVII. | Perspective View of Fixed Dioptric Light of First Order, with Catadioptric Zones. |
| XVIII. | Vertical Section of Fixed Dioptric Light of First Order, with Catadioptric Zones. |
| XIX. | Vertical Section of Catadioptric Light of Fourth Order, with Framing. |
| XX. | Elevation of Mechanical Lamp for Dioptric Lights of First Order. |
| XXI. | Enlarged Views of Oil-Pumps of Mechanical Lamp. |
| XXII. | Enlarged Views of Oil-Pumps of Mechanical Lamp. |
| XXIII. | Details of Clock-work of Mechanical Lamp. |
| XXIV. | Details of Clock-work of Mechanical Lamp. |
| XXV. | Flame of Mechanical Lamp of First Order at full size. |
| XXVI. | Elevation of Diagonal Lantern, and details of Astragals. |
| XXVII. | Elevation of Ardnamurchan Lighthouse. |
| XXVIII. | Plan of Ardnamurchan Lighthouse. |
| XXIX. | Lines of a Floating Light Vessel belonging to the Corporation of Trinity House of Deptford Strond. |
| XXX. | Elevation of Covesea Skerries Beacon. |
| XXXI. | Details of Covesea Skerries Beacon. |
| XXXII. | Elevations and Sections of Stone and Iron Beacons. |
| XXXIII. | Elevations of Buoys. |
| Page | 52, | line 8, for Redelet read Rondelet |
| ... | 178, | line 6, for L.93,306:8:10 read L.86,977:17:7 |
| ... | 292, | line 30, for radius rector read radius vector |
| ... | 294, | line 13, for give read gives |
| ... | 329, | line 3, for earth read sea |
| ... | 347, | line 29, for Plate XXXII., read Plate XXX., |
[7]
In the course of preparing the account of the building of the Skerryvore Lighthouse, it occurred to me, that a short Introduction should be prefixed, embracing a concise view of the constitution and acts of the Board of Commissioners of Northern Lights, more especially from 1824, when my Father’s work on the Bell Rock Lighthouse was published, up to the present time. This object will be best accomplished, by presenting to the reader, in the first place, an account of the constitution and powers of the Lighthouse Board, chiefly drawn from the “Introduction to the Bye-Laws, Rules, and Regulations of the Commissioners of Northern Lighthouses,” prepared by a Committee of their number; and by afterwards briefly noticing the principal works of the Board since 1824, and stating generally the nature of the changes and improvements made within that period on the mode of illumination, of which I propose, in a subsequent part of this volume, to give a somewhat detailed account.
The trade of Scotland had begun to increase very soon after the settlement of the civil war in 1745; but it was not till the year Constitution of the Lighthouse Board. 1784 that the general establishment of Sea Lights upon the Coast appears to have been brought under the notice of the Legislature. In that year, the subject was first mentioned at a meeting of the Convention of the Royal Burghs of Scotland, by Mr Dempster of Dunichen, M.P., the Provost of the burgh of Forfar; and, in the year 1786, that gentleman brought a bill into Parliament, and an Act was obtained establishing the present Board of Northern Lights.
[10]
This Act sets forth, that “it would conduce greatly to the security of navigation and the fisheries, if four Lighthouses were erected in the Northern parts of Great Britain, one on Kinnaird’s Head, Aberdeenshire, one in the North Isles of Orkney, one on the point of Scalpa, in the Island of Harris, and a fourth on the Mull of Kintyre, Argyllshire;” and it accordingly authorises the erection of those four Lighthouses. The Commissioners appointed for carrying this Act into execution were, the Lord Advocate and Solicitor-General of Scotland, the Lord Provost and first Bailie of Edinburgh, the Lord Provost and first Bailie of Glasgow, the Provosts of Aberdeen, Inverness, and Campbeltown, the Sheriffs of the counties of Edinburgh, Lanark, Renfrew, Bute, Argyll, Inverness, Ross, Orkney and Zetland, Caithness, and Aberdeen. An Act was subsequently passed, which authorised the Commissioners, when any new Lighthouse was established on any part of the coast of Scotland, to add to their number the Provost or Chief Magistrate of the nearest Royal Burgh, and also the Sheriff-Depute of the nearest county; and, by the exercise of this power of assumption, the board now includes the Sheriffs of the counties of Ayr, Fife, Forfar, Wigtown, Sutherland, Kincardine, and Kirkcudbright. To enable the Board to carry on the intended works and to provide the means of maintaining the Lights, those Acts gave power to the Commissioners to levy a duty of 1d. per ton on British vessels, and 2d. per ton on foreign vessels; and liability to pay this duty was incurred by all vessels passing any of the Lighthouses in the course of a voyage; but this single payment freed them from any farther exaction, although they should pass more than one Lighthouse in the course of the voyage. The Board held its first meeting at Edinburgh on 1st August 1786. A Secretary and Engineer were appointed, and a resolution was adopted to borrow L.1200. For this sum the Magistrates of the five Royal Burghs named in the Act interposed their security; and, at the same time, assigned, in farther security, the duties under the Act of Parliament. After appointing a Committee to prepare matters for a general[11] meeting, they adjourned till the 23d of January 1787. Some inconvenience having been felt in conducting the business of the Board, particularly in the holding of stock and other property, by reason of its not being an incorporated body, an Act was obtained for erecting the Commissioners into a body politic, by the name of the “Commissioners of the Northern Lighthouses.” Several Acts have been subsequently passed, in order to facilitate the erection of particular Lighthouses, and for the purpose of granting duties for their support. All those duties, however, are now abolished, and others have been substituted, the collection of which is regulated by an Act, 6th and 7th William IV., cap. 79, intituled, “An Act for vesting Lighthouses, Lights, and Sea-marks on the Coasts of England, in the Corporation of Trinity-House of Deptford Strond, and for making provision respecting Lighthouses, Lights, Buoys, Beacons, and Sea-marks, and the Tolls and Duties payable in respect thereof.” This Act declares, “That from the first day of January one thousand eight hundred and thirty-seven, the tolls now payable by or in respect of vessels for or towards the maintenance of the several lighthouses at present under the management of the Commissioners of Northern Lighthouses shall cease to be payable, and that, in lieu thereof, there shall thenceforth for ever be paid to the said Commissioners of the Northern Lighthouses, for every vessel belonging to the United Kingdom of Great Britain and Ireland (the same not belonging to his Majesty, his heirs or successors, or being navigated wholly in ballast), and for every foreign vessel which, by any Act of Parliament, order in Council, convention, or treaty, shall be privileged to enter the ports of the said United Kingdom, upon paying the same duties of tonnage as are paid by British vessels (the same not being vessels navigated wholly in ballast), which shall pass any of the said lighthouses, or derive benefit thereby, the toll of one halfpenny per ton of the burden of every such vessel for each time of passing every such lighthouse, or deriving benefit thereby, and of one penny per ton for each time of passing the Bell Rock Lighthouse,[12] and double the said tolls for every foreign vessel not so privileged.” And with regard to any new Lighthouses to be hereafter erected, it is provided, that there “shall be paid to the Commissioners by the owner, or other person having the command of any vessel not belonging to His Majesty, which shall pass such lighthouse, or derive benefit thereby, such reasonable toll as shall have been first approved in that behalf by His Majesty in Council.” Before the passing of this Act, the Commissioners had been uncontrolled in the selection of stations for Lighthouses, or in choosing the characteristic appearance for the Lights; but it being considered desirable to have a systematic arrangement in the three kingdoms, the Irish Lighthouse Board, as well as the Commissioners, are now required to give notice to the Corporation of the Trinity-House of Deptford Strond, before altering the character of any Light, or erecting any new Lighthouse; and that Corporation must, within the period of six months after receiving such notice, signify their opinion as to the propriety of the change, or the utility of any new Lighthouses submitted for their consideration. The Act, however, provides, that, if the Commissioners are dissatisfied with the opinion of the Trinity-House, they may appeal to the Privy Council, whose determination is final. By this Act, also, an important power is given to the Commissioners to control the exhibition of all harbour and local Lights, or other sea-marks, and to prevent the exhibition of any Lights or fires on the sea-coast, which might be mistaken for the regular Lights exhibited by the Board. In the Appendix I have given a copy of the Annual Statement of the Income and Expenditure of the Board for the year 1846, prepared by Mr Alexander Cuningham, the Secretary to the Commissioners.
Since the Sumburghhead Lighthouse in Zetland was lighted in the year Lights established since 1821. 1821, with a notice of which the account of the Bell Rock Lighthouse concludes, the Commissioners have been engaged in the establishment of seventeen new Lighthouses, and the remodelling of several old ones; and they have, more particularly,[13] effected important changes in the mode of illumination, and have begun to place Beacons and Buoys on the coast. They have, besides, executed several considerable improvements, for the purpose of facilitating the communication with the Lighthouses at Kintyre in Argyllshire, Cape Wrath in Sutherlandshire, and Dunnethead in the county of Caithness, by the establishment of landing-piers and the formation of roads, varying in length from three to ten miles, in connection with those Stations. Of those works, many interesting details might be given, were it not desirable that the introduction to an account of a single Lighthouse should be restricted within a very moderate compass; and I have, therefore, thought it sufficient to lay before the reader the most important circumstances of each Lighthouse Station belonging to the Board in a tabular form in the Appendix.
I shall not, in this place, enter on any exposition of the general principles which regulate the illumination of Lighthouses, and still less will it be proper to discuss the advantages of the different methods of illumination by Reflection and Refraction, as I shall, in the sequel, find a more convenient opportunity for speaking somewhat in detail on those subjects. It will be enough to present a very brief notice of the Improvements in the mode of illumination.improvements in the mode of illuminating Lighthouses, which the Northern Lights Board have introduced since 1824, up to which time, as already mentioned, a sketch of their works is already before the public. One of the most important changes in Lighthouse apparatus was, unquestionably, the introduction of Revolving Lights at the Tour de Corduan about the year 1780, by which the means of distinguishing one light from another were greatly extended, and a marked difference in the appearance of contiguous lights was at once simply obtained. The mere variation of the velocity of the revolution is so simple as to afford an obvious source of distinction among lights; and yet it is remarkable, that it was only lately that one of its principal advantages was perceived by my Father, who first applied it in the year 1827 as a means of distinction for the Light of Buchanness. This distinction consists in giving the frame a greater number of sides or[14] faces, and a more rapid revolution, so as to cause a flash in every five seconds of time, which produces an effect so marked and characteristic as to afford by far the most effective distinction which has been exhibited since the introduction of Revolving Lights. Under the auspices of the Board, this distinction has been since applied at the Rhinns of Islay Lighthouse, and has given much satisfaction wherever it has been tried. The late King of the Netherlands, a great patron of the useful arts, was so much pleased with this device that he presented the author of it with a splendid gold medal, in token of his approbation. The only other improvement on the Reflecting Lights, which I shall notice in this place, is that called the intermittent light, which is due to the same officer, and was by him introduced at the stations of Mull of Galloway, Tarbetness, and Barrahead. It consists of the apparatus of a fixed Light, in front of which two cylindric shades are alternately shut and opened by a vertical movement, so as to produce a sudden extinction and exhibition of the light, in a manner very difference from the gradual decline and growth of the flash, which is produced in revolving Lights by the attenuating effects of divergence on the penumbral portions of the light reflected from the mirror.
Dioptric Lights. The introduction of lenticular apparatus into Lighthouses has been the last great improvement effected in their illumination. So far back as the year 1823, the attention of the Commissioners was first called by their Engineer to the invention of the late Augustin Fresnel, who had succeeded in building polyzonal lenses of large dimensions, and in adapting to them a lamp of great power, having four concentric wicks supplied with oil by a clock-work movement like that of the Carcel lamp. A committee was appointed to consider this subject; and under its direction a long train of experiments was made with those instruments and with the paraboloidal mirrors which are generally used in British Lighthouses. The results of the experiments led the Board, in the summer of 1834, to send me on a mission to France, with instructions to report my opinion as to the comparative merits of the dioptric and catoptric[15] apparatus for the illumination of Lighthouses. Through the kindness of my friend M. Leonor Fresnel, Secretary of the Commission des Phares, who in the most liberal manner put me in possession of all the information which I required, and afforded me an opportunity of visiting the most important Lighthouses on the French coast, I was enabled on my return to report very fully my views on the various topics whose investigation had been committed to me by the Lighthouse Board.
The characteristics of the two systems of illumination by Reflection and Refraction may be briefly described as follows: In the reflecting apparatus, the lamp is placed in front of the mirror, whose surface is so formed that the rays which fall upon it, and are reflected from it, must afterwards move in lines parallel to the axis of the mirror; while in using Refracting instruments, the flame is placed behind the lens, whose action is simply to bend the rays in their passage through it, in such a manner that they come out from its face parallel to a line drawn from the focus to the centre of the lens. In Revolving Lights, on the reflecting principle, the mirrors containing the lamps are placed on a frame which revolves on its centre, and carries them round in succession to the different points of the horizon, so that each mirror produces a bright flash when it crosses the line drawn from an observer’s eye to the centre of the Lighthouse; but in Refracting Lights, a single lamp of great power is fixed in the centre of the lightroom, while the lenses, placed on a revolving frame, intercept and modify the rays which fall upon them from the Lamp, as they pass in front of it, and thus produce successive flashes whenever the centre of the lens crosses the imaginary line already noticed, as joining the observer’s eye and the lightroom.
In Fixed Lights, on the Reflecting plan, the mirrors are ranged around a fixed chandelier in tiers, one above another, their centres being placed in spiral lines, so that each shall subtend an equal arc of the horizon, and thus distribute the light with as little inequality as is consistent with the application of such an instrument as the[16] paraboloidal mirror to this purpose. This object of distributing the light equally over the horizon, which, next to intensity, is the main object of a fixed light, and ought, indeed, to be strictly co-ordinate with it, is much better effected by using dioptric instruments. That apparatus consists of successive rings or bent prisms arranged in the form of a hoop or belt, which may be described as a cylinder, generated by the revolution of the central section of a polyzonal lens about its focus as a vertical axis, and which consequently acts only in a vertical direction, leaving the natural horizontal divergence of the light unchanged, and thus distributing it with perfect equality in every direction.
Those two systems of illumination possess advantages and defects peculiar to each. The lenticular instruments insure greater intensity when applied to revolving lights; but this advantage is in part counterbalanced by the greater duration of the flash caused by the reflectors, whose divergence is greater; while in fixed lights, the refracting instruments not only produce at least an equal intensity of light, but, what is of the greatest importance, afford the same quantity of light in all directions, a property which fixed Lights on the reflecting principle employed in Britain cannot possess.
On my return from France I made a Report, which was printed by order of the Commissioners; and the views which I gave of the superiority of the refracting apparatus, led the Board to adopt the resolution of at once converting the revolving light of Inchkeith from the catoptric to the dioptric system, as its nearness to Edinburgh offered good opportunity of observation as to the effect of the change. In October 1835, the new light was exhibited to the public, and I was forthwith instructed to make a similar change on the fixed light of the Isle of May; but in carrying this into effect, I introduced an important modification of the form of the refracting part of the apparatus, with the view of obtaining a still nearer approach to the equal distribution of the light. The only other considerable change in the lightroom apparatus which has[17] since been effected, is the substitution of catadioptric zones in room of the mirrors hitherto used in the subsidiary parts of the larger French lights, which, as will appear in the sequel, was suggested by me in 1841, and finally carried into effect in 1843, agreeably to the computations of M. Leonor Fresnel. A Table of the Elements of those zones computed by myself, and closely verifying M. Fresnel’s results, will be found in the Appendix. The lenticular apparatus has been applied at the new Lighthouse stations of the Little Ross and the Skerryvore, and, still more recently, at Covesea Skerries, Cromarty Point, Chanonry Point, Loch Ryan, and Girdleness.
The establishment of a system of Beacons and Buoys. Beacons and Buoys on the coast of Scotland for the purpose of affording additional facilities to navigation, had long been looked upon as a desirable extension of the operations of the Northern Lights Board; and the increase of the trade and shipping of the kingdom having, some years ago, directed particular attention to the subject, a committee was named, on the 12th January 1839, to take special superintendence of that department. In 1840, the Engineer reported to the committee upwards of fifty stations for Beacons, and nearly a hundred for Buoys, as auxiliaries to the navigation in situations where the establishment of a Lighthouse was either too expensive or not warranted by the wants of the district; and means were immediately taken for erecting three Beacons in the Frith of Forth, two in the Clyde, one in Loch Ryan, and two in Cambeltown Loch. Beacons were also erected on the Iron Rock or Skervuile in the Sound of Jura, and on the Covesea Skerries in Morayshire, in connection with the Lighthouse of that name. Those works, notwithstanding many obstacles arising from doubts as to the powers of the Board, have been carried on with great vigour. In the Appendix, I have given drawings of three of those Beacons, one being of masonry, and the other two of iron; and also Tables which shew the positions of the various Beacons and Buoys at present belonging to the Board.
From the great difficulty of access to the inhospitable rock of Skerryvore, which is exposed to the full fury of the Atlantic, and is surrounded by an almost perpetual surf, the erection of a Light Tower on its small and rugged surface has always been regarded as an undertaking of the most formidable kind. So discouraging was the consideration of expense, and the uncertainty of the final success of such a work, that the Commissioners of the Northern Lighthouses, after successfully completing the arduous and somewhat similar work on the Bell Rock, were induced to proceed with other operations of less magnitude, but probably, in some respects, of no less utility; and to delay the construction of the Skerryvore Lighthouse till the present time, although the Act of Parliament authorising its erection was obtained so long ago as 1814.
The cluster of Rocks, of which that called the Skerryvore is the largest, has ever been a just cause of terror to the mariner. Its dangers have long been known, and the means of removing these dangers, by converting its dark horrors into a cheering guide for the benighted mariner, have often occupied the attention of the Lighthouse Board, and especially of my predecessor in the office of their Engineer, with whom it was a constant subject of interest, from its similarity to his own work on the Bell Rock.
The first landing that my Father, in the course of his annual voyages round the coast, as Engineer of the Northern Lighthouse Board, effected on Skerryvore, was in the year 1804. In 1814, he visited it a second time, while accompanying a committee of the Commissioners on a tour of inspection to the Lighthouses[20] all round the coast, from the Frith of Forth to the Clyde. On that occasion, Sir Walter Scott was of the party, and we find in his diary the following record of his impressions at the time, expressed in the terse and humorous language by which this interesting relic of the poet is characterised; and as the hasty observations of that great man seem worthy of a place in a work descriptive of the means which have been taken to obviate the dangers to which he refers, no apology seems necessary for introducing it in this place.
“Having crept upon deck about four in the morning,” says Sir Walter, “I find we are beating to windward off the Isle of Tyree, with the determination, on the part of Mr Stevenson, that his constituents should visit a reef of rocks called Skerry Vhor, where he thought it would be essential to have a Lighthouse. Loud remonstrances, on the part of the Commissioners, who, one and all, declare they will subscribe to his opinion, whatever it may be, rather than continue the infernal buffeting. Quiet perseverance on the part of Mr S., and great kicking, bouncing, and squabbling, upon that of the yacht, who seems to like the idea of Skerryvore as little as the Commissioners. At length, by dint of exertion, come in sight of this long ridge of rocks (chiefly under water) on which the tide breaks in a most tremendous style. There appear a few low broad rocks at one end of the reef, which is about a mile in length. These are never entirely under water, though the surf dashes over them. To go through all the forms, Hamilton, Duff,[1] and I, resolve to land upon these bare rocks, in company with Mr Stevenson. Pull through a very heavy swell with great difficulty, and approach a tremendous surf dashing over black pointed rocks. Our rowers, however, get the boat into a quiet creek between two rocks, where we contrive to land well wetted. I saw nothing remarkable in my way excepting several seals, which[21] we might have shot, but, in the doubtful circumstances of the landing, we did not care to bring guns. We took possession of the rock in name of the Commissioners, and generously bestowed our own great names on its crags and creeks. The rock was carefully measured by Mr S. It will be a most desolate position for a Lighthouse—the Bell Rock and Eddystone a joke to it, for the nearest land is the wild island of Tyree, at fourteen miles distance. So much for the Skerry Vhor.”
[1] The Sheriffs-Depute of Lanark and Edinburgh.
Notwithstanding those occasional visits, however, it was not till the year 1834, that the Commissioners directed their Engineer to make a survey of the whole of this extensive reef, preparatory to taking measures for the erection of a Lighthouse on that part of it which might be found, after careful inspection, to afford the most suitable site; and, at the same time, the shores of part of the Island of Tyree were surveyed, with the view of establishing a Signal Tower for communicating with the Lighthouse, and of forming a small harbour, of shelter for the vessels to be employed in attending it. From these surveys the general view of the Reef which is given in Plate II., and the enlarged plan shewn in Plate III. of the Skerryvore or principal Rock, on which the Lighthouse has been built, were constructed.
The Skerryvore or principal Rock of this remarkable group, is situated in North Lat. 56° 19′ 22″, and West Long. 7° 6′ 32″.[2] It is about 11 Nautic miles W.S.W ¹⁄₄ W. of the island of Tyree, which is the nearest land, 20 miles W.N.W ³⁄₄ N. of the island of Iona, 33 miles S. ¹⁄₄ E. of the Lighthouse of Barrahead, the most southern of the Hebrides, and 53¹⁄₂ miles N.E. by N. of Mallinhead, in the county of Donegal in Ireland. It may also be added, that the principal rock is about 50 miles from the nearest point of[22] the main land of Scotland. The extent of the Reef, and its situation in reference to the general position of the coast, will be best understood by referring to Plate I., which is a small Map of the British Isles. From this it will be seen that it lies in an irregular semicircular sea, inclosed by the southern extremity of the Hebrides, the rugged shores of Argyllshire, and the northern coast of Ireland on the one side, but open on the other to the Atlantic.
[2] According to information for which I am indebted to Captain Yolland, R.E., of the Ordnance Survey.
The importance of the Skerryvore as a station for a Lighthouse is so evident as to require but little comment. Although the smaller class of coasting vessels almost invariably sail through the sheltered Sounds of Mull, Loing, and Islay, to avoid the difficulties and dangers (Skerryvore among the number) of the rough navigation of the outward passage, yet these rocks lie much in the track of the larger vessels bound over seas round the North of Ireland from the Clyde and the Mersey. Government Cruisers and Ships of War are also necessarily often within a short distance of its dangers. But for homeward-bound vessels sailing for the Clyde, or for any of the Ports in the Irish sea, and directing their course for the North Irish Channel, the establishment of a light at this place is of the last importance. When such vessels happened to encounter bad weather before making land, and so had difficulty in ascertaining their true position in relation to the coast, they often, in the event of being driven so far north from their course, as to miss the lights of Ireland or that of Barrahead, continued their progress onwards in the direction of the Skerryvore Rocks; and thus, while running in apparent safety, and probably, from the state of the weather, not within sight of Tyree, which it is often difficult to see, they were very liable to encounter some of the many detached rocks and shoals which form this broken reef of nearly seven miles in extent.
In estimating the risks to which vessels were exposed from this cause, the peculiarly insidious nature of the danger must be[23] kept in view. A headland, or line of coast, which rises to some height above the surface of the sea can be seen in most states of the weather, at a sufficient distance, even during the night, to enable the seaman to avoid danger; but, in approaching a sunken reef or a low rock, in the dark, there is no object to warn the crew of their position, until their vessel gets unexpectedly among breakers, after which it is generally too late to bring her round again. And even the very knowledge of the existence of a reef, such as this, often causes the seaman, in ignorance of its exact position, to give it too wide a berth; in which case his ship is liable to be carried away by the force of tides or winds, perhaps on a lee shore, where, although the crew may be saved, the vessel generally goes to pieces.
The exhibition of a Light, however, altogether changes the case. Instead of shunning as a danger those dreaded rocks, vessels will steer boldly on their course, until checked by the Light, availing themselves of which they will be enabled to lie off-and-on during the night, and so wait the return of daylight, in perfect confidence as to their position, and without the necessity of endeavouring to avoid hidden dangers. Thus, that which was formerly an obstruction and a danger, is rendered an aid and a safety, to the navigation of the western coasts of our country.
That this source of danger to shipping was by no means imaginary, and the consequent terror of mariners far from being ill founded, there is a too melancholy proof in the following list of disasters caused by the Skerryvore Rock, and the neighbouring dangers off the coast of Tyree:—
| In | 1790. | The Ship Rebecca of 700 tons lost; crew saved. |
| 1804. | Ship Brigand of Nova Scotia, Wright, master, of 600 tons, lost off Hough, in Tyree; crew saved. | |
| 1804. | A Brig, M‘Iver, master, lost off Hough; crew saved.[24] | |
| 1806. | Ellen of Bath, Paterson, master, of 90 tons, lost off Balaphuil, in Tyree; one man drowned. | |
| 1809. | Brig Mary, Sanders, master, lost off Balaphuil; crew saved. | |
| 1813. | Sloop, Penelope of Wick, 60 tons, lost at Gott Bay, Tyree; crew saved. | |
| 1810. | A Brig from New York, Greenlees, master, lost off Hynish Point, Tyree; crew all drowned. | |
| 1813. | A Sloop, Eugene M‘Intyre, master, lost off Balaphuil; one man drowned. | |
| 1814. | Brig, Betsey of Leith, Ross, master, lost off Hough; crew saved. | |
| 1817. | A Brig, of 400 tons, foundered off Kennavarah, Tyree; crew all drowned. Numerous casks of butter came ashore. | |
| 1818. | Sloop, Benlomond of Greenock, M‘Lauchlan, master, lost off Balaphuil; crew all drowned. | |
| 1819. | Sloop, Bee, Coice, master, of 60 tons, lost off Hough; crew saved. | |
| 1820. | A Sloop, M‘Donald, master, of 50 tons, lost in Reef Bay, Tyree; crew saved. | |
| 1820. | Ship, Masters, of Port-Glasgow, Martin, master, of 700 tons, foundered off Skerryvore Rocks, and came ashore at Clate Hynish, in Tyree; crew saved. | |
| 1821. | Sloop, Catharine, M‘Rae, master lost; crew saved. | |
| 1821. | A Sloop, of 60 tons, lost off Hough; master and three men drowned. | |
| 1825. | Sloop, Dan of Campbelltown, M‘Innes, master, of 50 tons, lost; crew saved. | |
| 1828. | Sloop, Delight, of 70 tons, Stevenson, Master, lost. | |
| 1828. | An Irish Schooner of 100 tons, Montgomery, master, lost off Hough; crew saved. | |
| 1828. | Jane of Sligo, Collins, master, lost off Balaphuil. | |
| 1829. | Van Scapan of Stockholm, Fisherton, master, of 700 tons, lost off Hough; fourteen people drowned.[25] | |
| 1834. | Confidence of Dundee, Wesley, master, lost off Hough; crew saved. | |
| 1834. | A Schooner of 70 tons, lost; three men drowned. | |
| 1835. | Peggy, Bitters, master, of 500 tons, lost off Beist, Tyree; crew saved. | |
| 1841. | April 2. Majestic of North Shields, Tait, master, of 400 tons, foundered by a sea off Boinshly Rock, and came ashore at Gott Bay; captain and four men washed overboard and drowned, and the mate and one seaman had their legs broken when the vessel was struck by the sea. | |
| 1842. | Fleurs of Liverpool, Thomson, master, of 300 tons, lost off Kennavarah; crew saved. | |
| 1842. | March 14. Two deck beams, a knee, and some pieces of deck-plank of a North American built vessel, came ashore at Clate Hynish. | |
| 1842. | A Barra Boat wrecked, and four corpses washed ashore; two men, a woman and a child. | |
| 1842. | Pieces of wreck were seen in the Sound of Coll, and at the same time the shores of Tyree were strewed with candles, mostly of wax, supposed to be altar candles for the West Indies. | |
| 1843. | September 2. The Prussian Barque Formosa, of 326 tons, P. R. Reick, master, lost off Hough; two seamen drowned. | |
| 1844. | December 1. The Hull of a Sloop of about 70 tons, was washed ashore off Clate Hynish. The Hull was very much broken up by being in contact with the rocks; and one of the planks, apparently off the taffrail, had the words “Port of Dundee” lettered upon it; the crew supposed to be all drowned. |
This list is made up chiefly from data kindly furnished to me by the Rev. Neil Maclean, the Minister of Tyree and Coll, whose long residence on the former island has afforded him ample opportunity[26] for making observations on the subject. It is not to be imagined, however, that Mr Maclean’s list, which is made up from recollection, contains a full catalogue of the disasters caused by the Skerryvore, within the dates which it cites. Very many vessels were wrecked on this dangerous reef whose names could never be learned, and of which nothing but portions of the drift wood or cargo came ashore; and there have, no doubt, been many shipwrecks of which not a single trace has been left. Nothing, indeed, is more probable than that many of the foreign vessels whose course lay through the North Irish Channel, and whose fate has been briefly and vaguely described, as “foundered at sea,” have met their fate on the infames scopuli of the Skerryvore. It is also well known that the Tyree Fishermen were in the constant practice of visiting the Skerryvore, after gales, in quest of wrecks and their produce, in finding which they were but too often successful.
The natives of Tyree have many traditions of vessels having struck on the Skerryvore and gone to pieces; but, as might have been anticipated, few traces of this were to be found on the Rocks themselves, the breach of sea which sweeps over them during storms being sufficient to remove any heavy bodies which might be left there after a shipwreck. Some relics, however, were found during the progress of the works, and among the rest an anchor which was fished up close to the Rock, and which appeared to have belonged to a vessel of about 150 tons burden. It had been wasted to a perfect shadow by the action of the sea, and was covered with a thick coating of seaweed and barnacles. Although, however, the Rocks themselves do not retain the proofs of the disasters of which they have been the cause, the shores of the neighbouring Islands, during the progress of the works, were frequently strewed with drift wreck in such a manner as clearly to indicate what had taken place on the shoals round the Skerryvore.
On examining Plate II., it will be seen that what I have hitherto denominated the Skerryvore Reef, is a tract of foul ground,[27] consisting of various small rocks, some always above the level of the sea, others covered at high water, and exposed only at low water, and others, again, constantly under the surface, but on which the sea is often seen to break after heavy gales from the westward. This cluster of rocks extends from Tyree in a south-westerly direction, leaving, however, between that island and the rock called Boinshly, the first of the great Skerryvore cluster, a passage of about five miles in breadth, and having a depth of thirteen fathoms at low water of spring tides, but not without hidden dangers, which line the rugged shores of Tyree from Kennavarah to Ben Hynish, and some of which lie farther off than might be expected. This passage is called the passage of Tyree; but it is by no means safe during strong and long continued gales, as the sea which rises between Tyree and Skerryvore, is such that no vessel can live in it. I have myself often seen it one field of white broken water, the whole way from Tyree to the Rock; and we know that the wreck of the Majestic, which occurred in 1841, during the progress of the works, was entirely caused by the heavy seas which she encountered off Boinshly.
The principal rocks of the group, are called Boinshly, Bo-rhua, and Skerryvore, while those lying to the westward, which have been more recently laid down, have received the names of Mackenzie, Fresnel, and Stevenson.
The rock called Boinshly lies about 3³⁄₄ miles from Skerryvore, and is of considerable extent. The origin of the names of the different rocks in the vicinity of Tyree is by no means clear, and very little assistance or information is to be obtained in this matter from the natives. The name of Boinshly is probably derived from the Gaelic words boun, signifying bottom, and slighe, deceitful, as indicative of the dangers of the place; but other interpretations have been put on it, and that which has been now given is by no means certain. In the course of the survey, several soundings were[28] at considerable risk obtained, both upon this Rock itself, and in its immediate vicinity. The sea in that exposed situation is seldom so tranquil as to warrant an attempt to approach very near this Rock. The swell, which, in a greater or less degree, almost constantly prevails, is apt to impel, or seemingly draw the boat as by a kind of suction, upon the rock; and sometimes such accidents cannot be prevented, even although the greatest caution is used. Sudden lifts of the sea, during an apparent calm, are common in all the more exposed parts of the coast, more especially in the Orkney and Zetland Isles, and on the shores of the most western of the Hebrides; and any one much accustomed to the use of boats on these shores, must have experienced the hazard of encountering such unexpected risings of the sea, more especially near shelving rocks, or in rapid tide-ways. In some places the boatmen apply the name of lumps to these sudden waves. This effect is not felt to the same extent in attempting to reach a rock which is partially uncovered at low water, as a landing can, in such a case, often be effected on one side, at a time when the same rock on the opposite side, or a sunk rock just topping with the water, would, on every side, be quite unapproachable. From the soundings marked on the plan, it will be seen that shoal water extends all round Boinshly to distances varying from a quarter to half a mile. The sea breaks on the rock with great violence, and its position can easily be discovered from the island of Tyree by the white foam with which it is almost constantly surrounded, and which, in the heavy swells which sometimes accompany a dead calm, before or after a heavy gale of wind, rises to a prodigious height in a column or jet, resembling, at a distance, the play of a gigantic fountain. So high, indeed, does the sea rise on this shoal after heavy gales, that it often quite obscures the larger and more distant object of the Rock and Tower of the Skerryvore, even when viewed from the top of Ben Hynish in Tyree. The wooden barrack erected on the Skerryvore for the use of the workmen during the progress of the operations,[29] although about sixty feet in height, was often lost sight of at Tyree by the uprising of the sea on Boinshly, and could be seen only during the calm that intervenes between returning waves.
The next Rock that occurs is Bo-rhua, a name derived from the Celtic, and signifying, according to the natives, Red Rock. It lies about 2³⁄₄ miles from Boinshly, and about one mile from the Skerryvore. The passage between it and Boinshly is clear, and has a depth of about fourteen fathoms; but it is too narrow to be safely navigated except by daylight, even under the most favourable circumstances, and then no mariner would run the risk of taking such a passage, but would prefer, even at some sacrifice of time, the fairway of the passage of Tyree. Bo-rhua is completely covered at high, but is dry at low water. The extent of rock uncovered is about forty feet by twenty feet, and the highest point of it is about six feet above low water level of spring tides. A small outlying pinnacle, about ten feet square, is also uncovered at low water. The depth immediately round Bo-rhua is considerable, from three to seven fathoms being found within fifty feet of it; and in this respect it differs from Boinshly, which, as already mentioned, is surrounded by shoal water for some distance. Between Bo-rhua and Skerryvore, however, which is a distance of about a mile, there cannot properly be said to be any clear navigable channel, as will be distinctly seen by referring to the plan. The whole of this tract may, in fact, be termed foul ground.
The Skerryvore or chief rock, and the detached rocks immediately surrounding it, were surveyed with greater minuteness than the others, as it was at once apparent, that on this part of the reef alone could a suitable site for a lighthouse be found. The name is derived from the Gaelic, and signifies the Great Rock. It is very much wasted and cut up; the number of detached rocks, sunk and exposed, in its immediate neighbourhood, whose positions were determined during the survey, amounting to no fewer than 130. The[30] depth of water between those different detached fragments, which extend over a surface of about a mile in length, by half a mile in breadth, is considerable, varying from 2¹⁄₂ to 8¹⁄₂ fathoms at low water of spring tides.
The surface of the main or principal rock, on which the Lighthouse has been placed, measures, at the lowest tides, about 280 feet square. It is extremely irregular, and is intersected by many gullies or fissures, of considerable breadth, and of unlooked for depth, and which leave it solid only to the extent of 160 feet by 70 feet. The extremity of one of these gullies, at the south-east corner of the rock, forms the landing-creek, which is a narrow track of 30 feet wide, having deep water; and, with the help of some artificial clearing and dressing, which was executed with much difficulty, by blasting under water, while the other works were in progress, its sides and bottom are now comparatively smooth. At this place a landing can often be effected when the rock is unapproachable from any other quarter, although great inconvenience is felt from the surge, which finds its way from the opposite side of the rock, through the westward opening of the gulley in which the landing-place is situated.
Another of the gullies, immediately to the south-east of the Lighthouse, was found, on examination, to undermine the rock to the extent of eight or ten feet, and to terminate in a hollow submarine chamber, which threw up a spout or jet of water about twenty feet high, resembling in appearance the Geyser of Iceland, and accompanied by a loud sound like the snorting of some sea monster. The effect of this marine jet d’eau was at times extremely beautiful, the water being so much broken as to form a snow-white and opaque pillar, surrounded by a fine vapour, in which, during sunshine, beautiful rainbows were observed. But its beauties by no means reconciled us to the inconvenience and discomfort it occasioned, by drenching us whenever our work carried[31] us near it. One calm day I contrived, at a very low tide, by means of ropes and a ladder, to explore the interior of the cavern, from which this fountain rose, and found it to terminate in a polished spherical chamber, about seven feet in diameter, its floor filled with boulders, whose incessant play had hollowed it out of the veined rock, and rendered its interior beautifully smooth and glassy. As I considered that this curious cavern penetrated too far, and came too close to what I had selected as the best foundation, I changed the site of the tower, so as to avoid any chance of its being undermined. I also deemed it prudent to fill up the cavity, to prevent its further extension, and at the same time to rid ourselves of the discomfort of being drenched by the column of water which spouted up from it, even during fine weather, when the sea was apparently calm. This gulley affords a good example of the power of pebbles kept constantly in play by the waves to wear down the hardest rock, and shews what extensive effects so insignificant an agent may effect in the course of time.
Before the excavation for the foundation of the tower was made, a single conical loaf of rock, about five feet in diameter, rose to the height of eighteen feet above the level of high water, the greater part of the rest of its surface being about six feet above the tide mark.
In addition to its shattered and disjointed appearance, the Skerryvore Rock presents, in another respect, a striking example of the action of the sea, which no one, on first landing on the rock, can fail to perceive. I allude to the glassy smoothness of its surface, a feature that existed to so remarkable an extent as to have proved throughout the whole duration of the work, but more especially at its commencement, a serious obstacle and hindrance to the operations. It may, at first sight, appear strange that this grievance should have been so much felt; but, when I mention that the landings[32] were often made in very bad weather, it will be obvious that there was considerable danger in springing ashore from a boat in a heavy surf upon an irregular mass of rock as smooth and slippery as ice. The workmen were, in that respect, often sorely tried, and many inconvenient accidents occurred from falls. It was after one of these trials of patience, that the foreman of the masons was heard very graphically to describe a landing on the rock as “like climbing up the side of a bottle.” Instead of a weather-beaten rock, whitened by the dung of sea-fowls, and with marine crustacea adhering to it, the surface of the Skerryvore is smoothly polished by the action of the waves, every projecting angle or point is worn down, and the whole presents more the appearance of a mass of dark-coloured glass than a reef of gneiss-rock. Excepting in some of the more sheltered crevices, no marine crustacea find shelter; but different kinds of sea-plants grow upon it, in great abundance, at and below the low water mark. These plants are, doubtless, enabled to resist the action of the waves in the same way as the sapling, yielding to the blast, is preserved during the storm that uproots the aged and more stubborn oak.
The rocks of Skerryvore have the same characteristics as those of the neighbourhood of Tyree, being what we may, perhaps, call a syenitic gneiss, as it consists of quartz, felspar, hornblende, and also mica. It will be seen, from the narrative of the progress of the works, that this rock was, from its hardness, exceedingly difficult and tedious to excavate. The only variation in the geology of the Skerryvore, is the presence of a trap rock, in the form of a dyke of basalt, which intersects the strata, and exhibits a fine specimen of the intrusion of igneous rocks. It is shewn in Plate, No. III., by a thick black line.
Connected with this general view of the appearance and geology of the rock, it may be interesting also to notice, that a considerable mass of foreign matter, somewhat resembling, in its[33] structure, a deposit of lime, was found in different places resting in horizontal layers of various thickness and size. This substance was found in pools or sheltered parts of the rock, about the level of high water mark, and, in some cases, even a little below it. It was so hard as to admit of a pretty high degree of polish; and emitted an offensive odour on being burned in the fire, or rubbed on a stone with water. It gave other clear indications of containing animal matter, and in other respects resembled the bergmeal and guano. To account for its presence in such a situation, seems rather a difficult problem. On sending a specimen of this material to my friend the Rev. Dr Fleming, Professor of Natural Philosophy in King’s College, Aberdeen, I received from him an analysis of the substance, and a concurrence in the opinion I had formed as to its containing animal matter; and Dr Fleming, indeed, expressed his belief that the matter in question is the indurated soil of birds, and had been deposited when the reef was more extensive, and the resort, and probably the breeding-place of sea-fowls.[3] How this singular formation should be found on the verge of the ocean, and even within the high water mark, in spite of winds and waves, or how it should have assumed the stratified structure which seems to indicate the depositation of successive layers in still water, are matters very difficult to be explained, without coming to the conclusion, that the uncovered surface of Skerryvore Rock must at some distant period have been much more extensive than at present, so as to permit the deposit to go on in an interior basin or lagoon, sheltered from the waves, and somewhat similar to those which Dr Darwin has described as characteristic of the Coral Isles of the Pacific. This supposition seems not at all improbable, as it does not require a great stretch of fancy to conceive, that at some period, the whole of the rocks in the immediate vicinity of Skerryvore, and extending perhaps even so far as Bo-rhua, may have been connected by a matrix of softer materials, which have[34] gradually yielded to the action of the sea, leaving the harder portions to be smoothed and polished by the waves, and to assume the characteristic features of permanent rocks and sunk reefs which they now possess. There is also some countenance to such a view to be derived from the features of the neighbouring Island of Tyree, which contains numerous small lagoons, in which such deposits might be formed by the flocks of sea fowl which frequent them. Some of these pools are so near the shore, as to make it no difficult matter to conceive that their walls might be broken by the sea, and that they might eventually become part of it, and thus exhibit the phenomenon of deposits apparently lacustrine within the verge of the ocean.
[3] Dr Fleming has since obtained from Ichaboe indurated bird-soil or guano, closely resembling that from the Skerryvore.
Another remarkable feature which I observed in the Skerryvore Rock, was a deposit of gravel in the narrow crevices of the rock, which run nearly from north-east to south-west, dipping at an angle of 80° to the westward. In almost all of the fissures we found great quantities of small water worn boulders, less in size than a horsebean, and generally of the same materials as the rock itself. The boulders bore the appearance of having been forced into the fissures of the rock by some very powerful pressure, and were wedged hard into the crevices. In some cases a considerable quantity of softer matter containing iron was found, and in it the pebbles were imbedded. In the upper parts of the rock the crevices swarmed with centipedes of a reddish-brown colour. The rock was covered with sea fowl when first visited, and during heavy gales seals resorted to it.
About three miles to the westward of Skerryvore lie Mackenzie’s Rock, Fresnel’s Rock, and Stevenson’s Rock, which, as will be seen from Plate II., are connected by a tract of foul ground of about a mile and a quarter in length. Those rocks are the western limit of what we have already denominated the Skerryvore Reef. The passage between them and the Skerryvore or main rock is clear,[35] and has a depth of water varying from eleven to twenty-eight fathoms.
Mackenzie’s Rock, which derives its name from the celebrated Marine Surveyor, is uncovered, at low water, to the extent of about forty yards, and consists of scattered patches of rock, one of which, at its highest part, rises about ten feet above high water mark of spring-tides. Fresnel’s and Stevenson’s Rocks are always under water; but the sea is often seen to break violently over them, as well as over the whole stretch of the sunken reefs which extend between them. The first of those rocks is indebted for its name to the great optical philosopher, who so greatly improved lighthouses; and the second bears the name of the surveyor who first laid down the rock,—the late Engineer of the Northern Lights Board.
During the progress of the survey, a register of the rise and fall of the tides was regularly kept at Hynish on the neighbouring Island of Tyree; and from those observations it was determined, that the rise at that place is between twelve and thirteen feet at high spring tides, and three feet at dead low neap tides; and observations subsequently made while the works were in progress, gave the same results at the Rock of Skerryvore. It is high water at the Rock at full and change of the moon, at five hours and twenty-five minutes. The tides round the Skerryvore are not remarkable for their rapidity. In spring-tides the velocity is between four and five miles, and in neap-tides between two and three miles an hour. The flood sets to the N.N.E., and the ebb to the S.S.W.
In this chapter I shall very briefly notice those preliminary arrangements which may be said to have been in a great measure preparatory to the commencement of the work itself. It has been already stated, that the erection of the Lighthouse was provided for in the Act of 1814; but so formidable did this work appear, that although it was repeatedly under consideration, it was not until the General Meeting of the Board, on the 8th July 1834, that any measures were taken to carry into effect the provisions of the Act. On that occasion it was moved by the late Mr Maconochie, Sheriff of Orkney and Zetland, that the Engineer should be instructed to make the Survey of the Skerryvore Rocks. necessary survey, and to report as to the expense of erecting the Lighthouse. In terms of this remit, the survey of the Rocks was commenced in the autumn of 1834; but from the broken state of the weather, little was effected at that time beyond making the triangulation; and it was not until the summer of 1835 that the survey was completed from which the Chart, Plate No. II. was constructed. This survey was attended with much more labour than its extent would lead one to suppose, in consequence of its embracing the entire range of operations required in a more extensive nautical survey, and combining with the ordinary details required for a Chart, the minute accuracy in regard to surface and levels, which are always necessary for the purposes of the Engineer.
[38]
The first step was the measurement of a base line in the low lands of the adjoining Island of Tyree, which, owing to the distance and disadvantageous position of that island, could not be satisfactorily extended to the Rock without fixing stations in some of the more distant islands; and in the course of the work not fewer than twenty land triangles were measured. The calculations of the distances founded on this triangulation agreed with those afterwards obtained from the data of the Trigonometrical Survey, which were kindly furnished to me by Captain Yolland of the Royal Engineers, in 1843. For the purpose of making the soundings and laying down the sunken rocks, an entirely separate triangulation, based upon and connected with that which has already been noticed, became necessary, as the land objects were too distant, and their relative positions were such as to render it difficult by observations from them alone to determine any stations on the sea. Buoys were therefore moored at convenient points, and their positions determined by a subsidiary triangulation, so as to form a net-work of triangles between the shore and the Skerryvore Rock. The distances between these buoys were afterwards used as the bases of imaginary triangles, having points of sounding or shoals in their apex; and the angles subtended by those distances being measured by the sextant, the positions of the shoals or soundings were thence easily deduced and protracted on the Chart.[4] In connection also with the soundings whose positions were determined in the way above described, a complete set of tide observations was made, extending over a period of about six weeks. Those tide observations were connected in point of time, with the soundings, and were employed as the means of correcting the observed depths taken with the sounding-line, so as to give the true depth in reference to the high or low water of a given tide. Accurate measurements, and minute sections, were also made of the rocks in reference to the tide-level, and more especially of the main rock, on which[39] alone it was obvious, from the first inspection, that the Lighthouse Tower could be erected. In the course of this survey, the positions of upwards of 140 rocks were determined, and laid down on the Chart, and 500 soundings were taken, and their positions protracted. An interesting fact was also noticed regarding the mean level of all the tides which had been watched during the period of about six weeks, as above noticed, viz., that the point half way between the high and low water of every tide is on one and the same level. This fact regarding the tides was, it is believed, first detected by my Father, in the course of some tidal observations which he made in the Dornoch Frith in 1830, and has since been observed in the Frith of Forth in 1833, and again on the shores of the Isle of Man, and at Liverpool. The agreement of so many observations by various persons at places on the opposite shores of the Kingdom, seems to imply the universality of this phenomenon in the British Seas; and the position of Skerryvore would lead to the belief, that it is not confined to narrow seas, but that it exists in the ocean. I cannot dismiss the subject of the survey, without mentioning the late Mr James Ritson, who acted as principal assistant surveyor, and to whose zeal and intelligence so much of its accuracy is to be attributed. The deep gulley which intersects the main Rock from N.E. to S.W., and across which he one day sprang while it was filled with a breaking wave, bears his name, as a memorial of his activity and perseverance. At the close of the survey in 1835, the station-pole was left wedged and batted into one of the fissures or crevices of the Rock, and a cask of water was firmly lashed to ring-bolts in a cleft of the highest part of the Rock, in the hope that it might possibly prove useful to some shipwrecked seamen.
[4] Vide Stevenson’s Marine Surveying and Hydrometry. Edinburgh, 1842, p. 144.
For the purposes of navigation generally, a survey merely indicating the position and extent of the foul ground would have been sufficient. But in connection with the work which was about to be commenced, it was particularly desirable to have exact details of the depths, rocks, and shallows of the surrounding sea, with the[40] nature of the bottom, accurately laid down; and our experience during the course of the work, more than once shewed how essential was the possession of minute topographic information to the safety of the shipping attending the works; more especially as some of the vessels lay very near the rocks, and were frequently driven, by a sudden change of wind, to seek shelter, during the darkest nights, among the neighbouring islands.
Until this time the greatest ignorance prevailed amongst seamen as to the extent of the Reef, which had never before been minutely surveyed. Of this some proofs occurred even during the progress of the survey; for several vessels came so near the Rocks as to cause, in the minds of the surveyors, who witnessed their temerity, serious fears for their safety. On one occasion, in particular, a large vessel belonging to Yarmouth, with a cargo of timber, was actually boarded between Mackenzie’s Rock and the main Rock of Skerryvore by the surveyors, who warned the master of his danger in having so nearly approached these rocks, of the existence of which his chart gave no indication. On another occasion, a vessel belonging to Newcastle was boarded while passing between Bo-Rhua and the main Rock; and so little, indeed, had the master (whose chart terminated with the main Rock, and shewed nothing of Bo-Rhua) been dreaming of danger, or fancying that he was within a cable’s length of the reef, that he was found lying at ease on the companion, enjoying his pipe, with his wife sitting beside him knitting stockings.
Much preliminary investigation was necessarily occasioned by the difficulties and disadvantages arising from the remote situation of the island in which a great part of the works was to be carried on. Not only is the Rock itself often inaccessible and dangerous, being surrounded by numerous shoals, and visited by the heaviest seas of the Atlantic; but what gave rise to no small part of the difficulties which attended this work, was the nature of the neighbouring Island of Tyree. Disadvantages of Tyree. This island is unhappily destitute of any[41] shelter for shipping, a fact which was noticed as a hinderance to its improvement, upwards of 140 years ago, by Martin, in his well-known description of the Western Islands.[5] Nor is its interior more attractive; for although some parts of the soil when cultivated are excellent, the greater part of its surface is composed of sand. It was therefore obvious, at a glance, that Tyree was one of those places to which every thing must be brought; and this is not much to be wondered at, as the population, who, on a surface not exceeding 27 square miles, amounted in 1841 to 4687 souls, labour under all the disadvantages of remoteness from markets, inaccessible shores and stormy seas, and the oft-recurring toil of seeking fuel (of which Tyree itself is destitute) from the Island of Mull, nearly 30 miles distant, through a stormy sea. It is said that this total absence of fuel in Tyree is the result of the reckless manner in which it was wasted, in former days, in the preparation of whisky; but, however this may be, certain it is that the want of fuel greatly depresses the condition of the people. For our works, therefore, craftsmen of every sort were to be transported, houses were to be built for their reception, provisions and fuel were to be imported, and tools and implements of every kind were to be made.
[5] A Description of the Western Islands of Scotland, &c., by M. Martin, Gent. London, 1703. Vide 2d Edition of 1716, p. 267.
In the course of the survey, much attention had been bestowed upon the selection of a convenient place for a workyard in Tyree for the preparation of materials, and in examining its rugged shores in quest of the best site for a Harbour, for the shipment of the building materials for the Rock, and for the all-important purpose of enabling the future attending vessel to lie in safety within sight of signals from the Rock, when the Light should come to be exhibited to the public. The point chosen for this establishment was Pier and workyard at Hynish Tyree. Hynish, which, though twelve miles distant, is, nevertheless, the nearest creek to the Skerryvore Rock, and which,[42] however exposed it may be, if compared with creeks elsewhere dignified with the name of Harbour, certainly affords as good prospect of shelter as any other part of the Island of Tyree, and is, in this respect, greatly to be preferred to any other place within sight of the Rock. A deputation of the Commissioners visited the Skerryvore in the month of July 1836, and concurred with the Engineer in regard to his choice of Hynish as a site for the Harbour and establishment.
Another most important point of inquiry was regarding the materials for building the Lighthouse; and on this subject the suggestions in a Report by the Engineer, of the 31st December 1835, were followed, which proposed the opening of quarries among the gneiss rocks around Quarries at Hynish. Hynish. Much facility was afforded by the liberality of the late Duke of Argyll, the proprietor of Tyree, who granted to the Commissioners free permission “to quarry materials for the purpose of the Lighthouse, on any part of the Argyll estates.” This freedom was generously continued by the present Duke, who has all along taken a lively interest in the success of the works. In terms, therefore, of the Engineer’s recommendations contained in the above noticed Report, Mr James Scott and fourteen quarriers were employed, during the summers of 1836 and 1837, in opening quarries, with very promising appearances of final success, among the gneiss rocks near Hynish Point. In the summer of 1837, Mr Scott and his party turned out about 3800 cubic feet of rock, capable of being applied to the purposes of squared masonry, and a very large quantity of stones fit for rubble work. This produce, although small, if contrasted with that of established quarries, is by no means despicable, when the force employed and all the disadvantages of the situation are considered; and if the nature of the material, which is full of rents and fissures (technically called dries and cutters), the frequent deceptions attending the opening of new quarries, the excessive hardness and unworkable nature of the rock, the quality and size of the blocks required to entitle them to claim a place in a marine tower, and the great[43] loss of time, caused by the badness of the weather, be considered, it will not appear that Mr Scott and his party had been eating the bread of idleness.
In the mean time, measures had been taken for obtaining from his Grace the Duke of Argyll a feu of fifteen acres of ground at Hynish, for carrying on the works, with a view to its being finally occupied as an establishment for the crew of the vessel which was to attend the Lighthouse, and the families of the four lightkeepers, as well as for the site of the harbour. To this was added a lease of thirty acres, for the various purposes connected with a workyard, and such an establishment as seemed necessary for carrying on the work. A subject of anxious deliberation with the Board, was the construction of the harbour at Hynish for the vessels engaged in the service of the work; and the Commissioners, on the 24th May 1837, authorized the Engineer to make arrangements for commencing the formation of the Pier. The work was, accordingly, undertaken, in terms of his Reports of the 31st December 1835, and 27th February 1836; and the summer of 1837 was chiefly occupied in preparing a wharf, mostly composed of pierres-perdues,[6] and in the opening of the quarry already noticed. Such may serve as a brief and somewhat desultory notice of the work during the seasons of 1836 and 1837, after which it appeared to the Board that the operations must soon assume such an aspect as to require the superintendence of a committee of their number, as well as that of an Engineer specially entrusted with the management of the work.
[6] Blocks rough from the quarry, which are dropt or thrown promiscuously into the sea.
At the meeting of the Board, on the 8th December 1837, a Committee of their number was accordingly named, to superintend the erection of the Lighthouse. Skerryvore Committee appointed. This Committee consisted of—Robert Bruce, Esq., Sheriff of Argyllshire; Andrew Murray,[44] Esq., Sheriff of Aberdeenshire; Robert Thomson, Esq., Sheriff of Caithness; and the late James Maconochie, Esq., Sheriff of Orkney and Zetland; and, shortly after its appointment, the Committee, on the motion of Mr Bruce, the Chairman, appointed me Engineer for the work.
Among the first matters which engaged the attention of this Committee, was a Report from the Engineer, dated the 30th January 1838, in which the necessity of erecting a wooden barrack, as a place of shelter for the workmen on the Rock, was pointed out; the general arrangements for carrying on the operations were described; and the building of a steam-tender, to act as a towing vessel for the stone lighters between the workyard in Tyree and the Rock, was also recommended. The Report was accompanied by a detailed requisition or estimate for the operations of the ensuing season, amounting to L.15,000 : 3 : 3; of which sum it was proposed to expend about one-third in building a steam-tender, and the rest in erecting the wooden barrack on the Rock, and in providing tools and materials for the work, as well as in the wages of men to be employed in preparing the foundation of the Lighthouse Tower, and in building the Pier, and dressing stones at Hynish.
The Committee, after considerable deliberation, sanctioned the various items of the estimate, but hesitated to embark in the expense of building a steamer, until a fruitless correspondence with various ports of the kingdom, with the view of purchasing an old vessel, satisfied them of the necessity of building a tender expressly for the purpose.
Offers were immediately received from various parties at Greenock for the preparation of the wooden barrack, which was soon afterwards commenced by the late Mr John Fleming, house-carpenter, who was the successful competitor.
[45]
In this chapter I purpose, in the first place, to make a few observations regarding the construction of Lighthouse Towers in situations which are exposed to the assault of the waves, and afterwards to give a short notice of the design which I adopted for the Tower on the Skerryvore Rock. In making a design for a Lighthouse Tower in an exposed situation, numerous considerations at once present themselves to the Engineer; and it is difficult to assign to any one of them a priority in the train of thought which eventually conducts him to the formation of his plan. These considerations, however, may be conveniently divided into two classes:—1st, Those which refer to elements common to Lighthouses in all situations, and differ only in amount, such as the height of the Tower necessary for commanding a given visible horizon, and the accommodation required for the Lightkeepers and the Stores; and, 2d, Those which are peculiar to Towers in exposed situations, and which refer solely to their fitness to resist the force of the waves which tend to destroy them. The first class of considerations is so extremely simple, as to require few remarks in this place. The distance at which it is desirable that a light should be visible being ascertained, with reference to the nature of the surrounding seas and the extent to which any dangerous or foul ground lies seaward of the proposed Lighthouse, the height of the Tower is at once determined[46] by means of the known relations which subsist between the spheroidicity of the earth, the effects of atmospheric refraction, and the height required for an object which is to be seen from a given distance. The question regarding the space to be provided in the interior of the Tower, can only be properly answered by a person who has a minute practical acquaintance with the peculiar wants and the internal economy of Lighthouses. The accommodation required for Lighthouses in exposed situations must, in a considerable degree, depend upon the greater or less facility of access to them, and the opportunities for replenishing the stores of all kinds which are in daily consumption. In such places, also, the risk of accidents naturally leads to the precaution of retaining additional Lightkeepers, and of having duplicates or even triplets of those parts of the apparatus that are liable to be injured. Of such circumstances, corresponding extension of the space devoted to the reception of Stores and the accommodation of the Lightkeepers, is the necessary consequence. In the long nights of a Scotch winter, when the lamps are kept burning for about seventeen hours, during which time they are never left for a moment without the superintendence of at least one Keeper, the care of the light, even in the most favourable situations, necessarily occupies at least two persons; but in places like the Eddystone, the Bell Rock, and the Skerryvore, where it sometimes happens that six or eight weeks elapse without its being possible to effect a landing, it has been thought necessary that there should never be fewer than three Keepers on duty. This addition to the ordinary establishment of a Lighthouse calls for a greater number of sleeping-cabins, and, at the same time, involves a corresponding increase in the supply of water, fuel and other provisions, requiring much additional stowage. So far, therefore, a Light Tower in an exposed situation, differs from one on shore only in the extent of its internal accommodation.
The second class of considerations, which must guide the Engineer in framing a design for a Light Tower which is exposed[47] to the force of the waves, refers solely to the stability of the building.
The first observation which must occur to any one who considers the subject is, that we know little of the nature, amount and modifications of the forces, on the proper investigation of which the application of the principle which regulates the construction must be based. When it is recollected, that, so far from possessing any accurate information regarding the momentum of the waves, we have little more than conjecture to guide us, it will be obvious, that we are not in a situation to estimate the power or intensity of those shocks to which Sea Towers are subject; and much less can we pretend to deal with the variations of these forces which shoals and obstructing rocks produce, or to determine the power of the waves as destructive agents. No systematic or intelligible attempt has been made practically to measure the force of the waves, so as to furnish the Engineer with a constant to guide him in his attempts to oppose the inroads of the ocean. The only experiments, indeed, on the subject, with which I am acquainted, are those of Mr Thomas Stevenson, Civil-Engineer, who had long entertained the idea of registering the force of the impulse of the waves, and lately contrived an instrument for the purpose, which he has applied at various parts of the coast. I therefore gladly avail myself of the present opportunity, to give a brief statement of the results indicated by it, as contained in a paper by the inventor, which appeared in the Transactions of the Royal Society of Edinburgh of 20th January 1845, and of which a digest will be found in the Appendix, as any attempt to throw light upon this most obscure, but highly important subject, cannot fail to be interesting, not merely to the philosopher, but to the Marine Architect. It would naturally be expected, that the force of the waves should vary according to the season of the year, and the nature of the exposure, and this expectation is fully justified by the indications of the Marine Dynamometer. Thus it appears,[48] that during five summer months of 1843 and 1844, the average indications registered at different places near Tyree and Skerryvore, gave 611 lb. of pressure per square foot of surface exposed to the waves; while the average for the winter months for the same places during those two years, gave 2086 lb. per square foot, or upwards of three times that of the summer months. It also appears, that the greatest result as yet obtained at Skerryvore Rock was 4335 lb. per square foot; while that observed on the Bell Rock was 3013 lb., or one-fourth part less than that of Skerryvore. But these experiments have not been continued long enough as yet to render them available for the Engineer. In the present state of our information, therefore, we cannot be said to possess the elements of exact investigation, and must consequently be guided chiefly by the results of those numerous cases which observation collects, and which reason arranges, in the form which constitutes what is called professional experience. This kind of experience can only be acquired by long habit in carefully observing the appearance and effects of waves in different situations, and under various circumstances. We must attend to their magnitude and velocity, their level in regard to the rocks on which they break, the height of the spray caused by their collision against the shore, the masses of rock which they have been able to move, and those which have successfully resisted their assault; as also, where such exist, the slopes of the shores produced by the waves, viewed in connection with the nature of the materials composing the beach, with many other transient features which an experienced eye seizes and fixes in the mind as elements of primary importance in determining the power of the sea to produce certain effects. Such phenomena, with all their features and circumstances, we may carry in our recollection; and by comparing them with what has been observed at places where we know that artificial works have resisted the shocks of the waves, we may in some cases successfully arrive at a conclusion as to what works will, at all[49] events, be within the bounds of safety. We must not, however, in any case, venture to approach too near the limit of stability, so long as we continue to labour under our present disadvantages of defective information on some of the most important elements in the inquiry. If it be asked, therefore, how the size and form of buildings exposed to the shock of the waves are to be determined, the answer must be, that, in any given case, the problem is to be solved chiefly by the union of an extensive knowledge of what the sea has done against man, and how, and to what extent, man has succeeded in controlling the sea; together with a cautious comparison of the circumstances which modify and affect any given case which has not been the object of direct experience; nor does it seem possible as yet to found the art of Engineering, in so far as it refers to this class of works, upon any more exact basis. The uncertainty which must ever attend such reasoning can only, it is obvious, be dispelled by actual experience of the result; and time only can test the success of our schemes in cases of difficulty.
A primary inquiry, in regard to Towers in an exposed situation, is the question, whether their stability should depend upon their strength or their weight; or, in other words, on their cohesion, or their inertia? In preferring weight to strength, we more closely follow the course pointed out by the analogy of nature; and this must not be regarded as a mere notional advantage, for the more close the analogy between nature and our works, the less difficulty we shall experience in passing from nature to art, and the more directly will our observations on natural phenomena bear upon the artificial project. If, for example, we make a series of observations on the force of the sea, as exerted on masses of rock, and endeavour to draw from these observations some conclusions as to the amount and direction of that force, as exhibited by the masses of rock which resist it successfully and the forms which these masses assume, we shall pass naturally to the determination of the mass and form of a building which may be capable of opposing similar forces, as we conclude, with some reason, that the mass and[50] form of the natural rock are exponents of the amount and direction of the forces they have so long continued to resist. It will readily be perceived, that we are in a very different and less advantageous position when we attempt, from such observations of natural phenomena, in which weight is solely concerned, to deduce the strength of an artificial fabric capable of resisting the same forces; for we must at once pass from one category to another, and endeavour to determine the strength of a comparatively light object which shall be able to sustain the same shock, which we know, by direct experience, may be resisted by a given weight. Another very obvious reason why we should prefer mass and weight to strength, as a source of stability, is, that the effect of mere inertia is constant and unchangeable in its nature; while the strength which results, even from the most judiciously disposed and well executed fixtures of a comparatively light fabric, is constantly subject to be impaired by the loosening of such fixtures, occasioned by the almost incessant tremor to which structures of this kind must be subject, from the beating of the waves.[7] Mass, therefore, seems to be a source of stability, the effect of which is at once apprehended by the mind, as more in harmony with the conservative principles of nature, and unquestionably less liable to be deteriorated than the strength, which depends upon the careful proportion and adjustment of parts.
[7] It was chiefly on these grounds that the Commissioners of Northern Lights, after consulting a Committee of the Royal Society of Edinburgh, and Messrs Cubitt and Rennie, Civil Engineers, rejected the design of Captain Sir Samuel Brown, R. N., who volunteered a proposal to build an Iron Pillar at the time that the erection of the Skerryvore Lighthouse was determined on in 1835.
Having satisfied himself that weight is the most eligible source of stability, the next step of the Engineer is to inquire what quantity of matter is necessary to produce stability, and what is the most advantageous form for its arrangement in a tower. The first question, which respects the mass to be employed, is, as already stated, one of the utmost difficulty, and can be solved by experience[51] alone, directed by that natural sagacity which Smeaton, in his account of his own thoughts on the subject, with much naïveté, terms ‘feelings,’ in contradistinction to that more accurate process of deduction which he calls ‘calculation.’ It is very difficult, for example, to conceive that the waves could displace a cylindric block of granite, 25 feet in diameter and 10 feet high, which would contain about 380 tons, and we almost feel that they could not do so. If, in order to test the soundness of this expectation, we appeal to such experience as we possess, and apply to the largest vertical section of such a solid, the greatest force yet indicated by my brother’s Marine Dynamometer, which, as already stated, is 4335 lb. per square foot, we shall obtain a pressure of 484 tons, which, being reduced by one-half[8] for the loss of force occasioned by the convexity of the opposing cylindric surface, gives 242 tons, as the greatest force of the waves tending to displace the cylinder. But in the extreme case we have now supposed the solid will be entirely immersed in the water, and its efficient weight will thus be reduced by 140 tons, or the weight of an equal bulk of sea-water; and the remaining weight of 240 tons, by which it will resist the force of the waves, will be almost exactly equal to the pressure which they exert. This imaginary cylinder may, however, be regarded as still within the limits of safety, because the waves could not overturn it, unless their pressure exceeded the weight of the block in a ratio greater than that of its diameter to its height, which in this case is that of 25 to 10, or 2¹⁄₂ times. In order, therefore, to endanger the stability of the solid by overturning it, the pressure, instead of being 240 tons, must be 600 tons.[9] We have thus seen, that the cylinder is secure from the chance of being overturned; but we have yet to consider how far it is exempt from the risk of being displaced by the pressure of the waves, causing it to slide along the surface of the Rock, owing to deficiency of friction between[52] the two surfaces in contact. The block, for our present purposes, may be regarded as monolithic, either being really so or as a mass composed of parts so united by joggles, treenails and mortar, as to be free from any tendency to disintegration by the force of the waves; and in this case the stability of the cylinder will depend upon the amount of friction opposing the pressure of the waves which tends to produce a sliding movement. It appears, by some experiments of M. Rondelet,[10] that the friction of a block of stone sliding on a chiselled floor of rock is equal to ⁷⁄₁₀ths of its own weight; and we should thus obtain in the present instance 168 tons, as the amount of friction tending to resist the pressure of the waves, which would therefore exert a power superior to that resistance by 74 tons.[11] But this excess of force would be easily neutralized by the adhesion of the mortar and the abutment of the block against the sides of the foundation pit into which Lighthouse Towers in such exposed places are generally sunk in the solid rock. When, in addition to these considerations, we learn that the solid frustum, or lower part of the Eddystone Tower, which has weathered so many storms for the last ninety years, does not greatly exceed in mass the imaginary cylindric block which I have spoken of, our confidence in the stability of the cylinder is greatly increased. Our belief receives a still farther confirmation from the fact, that the strongest instance recorded of the power of the waves, falls considerably short of the case which we have just imagined. The instance alluded to is given in Mr Lyell’s Geology, on the authority of the Reverend George Low, of Fetlar, in Zetland, who mentions, that a block, whose dimensions seem to give us reason to estimate its weight at nearly 300 tons (or about one-fifth less than that of the cylinder), was moved over a point,[53] and thrown into the sea; and it must be remembered, that the form of this block, which was only 5 feet thick and about 40 feet long, rendered it very susceptible of a sliding motion, and must have greatly aided its transport. We may therefore not unreasonably conclude, that, in designing such a tower, it is safe to assume a mass which our own judgment and recorded facts seem to concur in pronouncing beyond the power of the greatest waves, as fixing the lowest limit to which the contents of the proposed edifice may be reduced.
[8] This reduction seems to be warranted by the results of some experiments of Bossut.
[9] This is the product of 240 tons, by the ratio of 2·5.
[10] L’art de bâtir.
[11] The number 168 is ⁷⁄₁₀ths of 240, which is the weight of the cylinder, reduced by the weight of an equal bulk of salt water; and 74 is the excess of 242 tons, the pressure of the waves, above 168, the amount of friction.
There are several circumstances, however, which tend to increase or diminish the stability of the same mass exposed to the same forces. Of these a very prominent one is the form of the mass, which may be so modified as to offer more or less resistance to the forces which assault the building. Thus a parallelopiped would be a much less suitable form for a sea tower than a cylinder, and so proportionally of all the polygonal prisms which may occur between these two extremes. I remember having heard it proposed, in the course of conversation, by a non-professional friend, that Lighthouse Towers might be formed in such a manner, that each horizontal section should be a wedge with its narrow end directed to the greatest assaulting force. This notion is in itself not destitute of ingenuity; for, if the circumstances to which it is to be adapted were constant, we should thereby present the form of least resistance, and, at the same time, the greatest depth and strength of the building to the line of greatest impulse. But the notion is wholly impracticable, because the direction of the winds and waves is so variable, as to render it almost certain that a Tower so constructed would, on some occasion, be assaulted in the line of its thinnest section; and thus, what might in one case be an advantage, would, in the event of such a change in the point of attack, become a great source of weakness, as the flat side of the wedge would then be opposed to the force, thereby presenting to the direct[54] assault of the waves the largest surface, with, at the same time, the most disadvantageous disposition of the resisting matter. There seems little reason, therefore, for any doubt as to the circular section being practically the most suitable for a Tower exposed in every direction to the force of the waves.
Next to this, and hardly to be separated from it, inasmuch as it involves the question regarding the form of the Tower, is the position of the centre of gravity. The stability of any solid will, in general, greatly depend upon its centre of gravity being placed as low as possible; and the general sectional form which this notion of stability indicates is that of a triangle. This figure revolving on its vertical axis, must, of course, generate a cone as the solid, which has its centre of gravity most advantageously placed, while its rounded contour would oppose the least resistance which is attainable in every direction. Whether, therefore, we make strength or weight the source of stability, the conic frustum seems, abstractly speaking, the most advantageous form for a high Tower. But there are various considerations which concur to modify this general conclusion, and, in practice, to render the conical form less eligible than might at first be imagined. Of these considerations, the most prominent theoretically, although, I must confess, not the most influential in guiding our practice, is, that the base of the cone must in many cases meet the foundation on which the Tower is to stand, in such a manner, as to form an angular space in which the waves may break with violence. The second objection is more considerable in practice, and is founded on the disadvantageous arrangement of the materials, which would take place in a conic frustum carried to the great height which Lighthouse Towers must generally attain, in order to render them useful as sea-marks. Towards its top, the Tower cannot be assaulted with so great a force as at the base, or, rather, its top is entirely above the shock of heavy waves; and, as the conoidal solid should be prolate in proportion to the intensity of the shock[55] which it must resist, it follows that, if the base be constructed as a frustum of a given cone, the top part ought to be formed of successive frusta of other cones, gradually less prolate than that of the base. But it is obvious, that the union of frusta of different cones, independently of the objection which might be urged against the sudden change of direction at their junction, as affording the waves a point for advantageous assault, would form a figure of inharmonious and unpleasing contour, circumstances which necessarily lead to the adoption of a curve osculating the outline of the successive frusta composing the Tower; and hence, we can hardly doubt, has really arisen in the mind of Smeaton the beautiful form which his genius invented for the Lighthouse Tower of the Eddystone, and which subsequent Engineers have contented themselves to copy, as the general outline which meets all the conditions of the problem which they have to solve. And here I cannot help observing, as an interesting, and by no means unusual, psychological fact, that men sometimes appear to be conducted to a right conclusion by an erroneous train of reasoning; and such, from his “Narrative,” we are led to believe, must have been the case with Smeaton in his own conception of the form most suitable for his great work. In that “Narrative” (§ 81), he seems to imply, that the trunk of an oak was the counterpart or antitype of that form which his (§ 246) “feelings, rather than calculations,” led him to prefer. Now, there is no analogy between the case of the tree and that of the Lighthouse, the tree being assaulted at the top, and the Lighthouse at the base; and although Smeaton goes on, in the course of the paragraph above alluded to, to suppose the branches to be cut off, and water to wash round the base of the oak, it is to be feared the analogy is not thereby strengthened; as the materials composing the tree and the tower are so different, that it is impossible to imagine that the same opposing forces can be resisted by similar properties in both. It is obvious, indeed, that Smeaton has unconsciously contrived to obscure his own clear conceptions in his attempt[56] to connect them with a fancied natural analogy between a tree which is shaken by the wind acting on its bushy top, and which resists its enemy by the strength of its fibrous texture and wide-spreading ligamentous roots, and a tower of masonry, whose weight and friction alone enable it to meet the assault of the waves which wash round its base; and it is very singular, that, throughout his reasonings on this subject, he does not appear to have regarded those properties of the tree which he has most fitly characterized as “its elasticity,” and the “coherence of its parts.” One is tempted to conclude that Smeaton had, in the first place, reasoned quite soundly, and arrived by a perfectly legitimate process at his true conclusion; and that it was only in the vain attempt to justify these conclusions to others, and convey to them conceptions which a large class of minds can never receive, that he has misrepresented his own mode of reasoning. In the paragraph preceding that which refers to the tree (§ 80), he has, in point of fact, clearly developed the true views of the subject; and, with the single exception of the allusion to the oak, he has discussed the question throughout in a masterly style.
In a word, then, the sum of our knowledge appears to be contained in this proposition—That, as the stability of a sea-tower depends, cæteris paribus, on the lowness of its centre of gravity, the general notion of its form is that of a cone; but that, as the forces to which its several horizontal sections are opposed decrease towards its top in a rapid ratio, the solid should be generated by the revolution of some curve line convex to the axis of the tower, and gradually approaching to parallelism with it. And this is, in fact, a general description of the Eddystone Tower devised by Smeaton.
No. 1.

It is deserving of notice, as one of the many proofs which the records of antiquity afford of the similarity of the results of human thought in all ages, and of the truth of the Wise Man’s saying, that “there is nothing new under the sun,” that the ancient Egyptians[57] appear to have had the same conceptions of the solid of stability that were present to the mind of the modern Engineer of the Eddystone Lighthouse. In the admirable work recently published by Sir J. Gardner Wilkinson on the Manners and Customs of the Ancient Egyptians, he gives, in the first volume of his second series, at page 253, a wood-cut, shewing the figure of the deity Pthah, under the symbol of stability, according to Egyptian conceptions. This symbol so closely and strikingly resembles the general appearance of the Eddystone, that I willingly give it a place in the text, (No. 1) denuded, however, of the arms and head-dress of the deity whom it shrouds.
In applying these general notions to the design of a Tower for the Skerryvore Rock, I was, of course, guided by numerous circumstances, which modified my views and produced the individual form of Tower which I have adopted. Since the days of Smeaton, when his magnificent Tower was lighted by common candles, the application of optical apparatus to Lighthouses has greatly altered the state of the case; and the improvement of the system in modern times has, in most instances, rendered a greater altitude of Tower desirable, in order to extend, as much as possible, the benefit of a system capable of illuminating the visible horizon of any Tower which human art can reasonably hope to construct. In the particular case of the Skerryvore, also, the great distance of the outlying rocks (some of which, as will be seen from the chart, are 3 miles right seaward of the Lighthouse) concurs with the improvement of the Lights, in making it desirable that the Tower should be of considerable height, and that the light should command an extensive range. It was, therefore, from the first consideration of the subject, determined that the Light should be elevated about 150 feet above high water of spring tides, so as to illuminate a visible horizon of not less than 18 miles of radius; and, after much deliberation, and a full consideration of the infrequency of communication with the proposed[58] Lighthouse from the great difficulty of landing on the Rock, and the consequent uncertainty of keeping up the supplies, I found that, for the convenient accommodation of the Lightkeepers and the suitable stowage of the stores, a void space of about 13,000 cubic feet would be required. These elements being fixed, the general proportions of the Tower came next to be considered.
In the Eddystone the radius of the base, at the level of high water of spring tides, is somewhat less than one-fifth of the height of the Tower above that level; while in the Bell Rock, at the same level, it is little more than one-seventh of the height. If, again, we suppose the curve of the Eddystone to be continued downwards to the level of low water, the radius (in so far as we may judge from sketching the continuation of a curve undefined by any geometrical property) would be rather more than one-fourth of the whole height above that level; while in the Bell Rock the proportion, in reference to the same level, is a little more than one-fifth. Viewing the whole height of the Skerryvore Tower above high water of spring tides as equal to 142 feet, and finding that, in the cases of the Eddystone and the Bell Rock, the radius of the horizontal section at that level is respectively one-fifth and one-seventh of the whole height; and again, viewing the extreme height of the Skerryvore Tower above low water of spring tides as equal to about 155 feet, and considering the proportionate radii of the Bell Rock and Eddystone (in so far as the latter is ascertainable) as respectively one-fifth and one-fourth of the heights of the top of the masonry above the level of low water, I finally decided upon giving the Tower at the Skerryvore such dimensions as would not be widely discordant with these general proportions. In this view, I determined that the radius of the base should not exceed 22 feet, on the level of about 4 feet above the high water mark, where I expected to obtain a solid foundation—a base which bears to the whole height of the Tower a proportion somewhat less than that of the Bell Rock, which is one-fifth.[59] It so happens, that the diameter adopted is nearly the greatest which the Rock affords; for, although a glance at the accompanying plan of the Rock at high water (Plate, No. III.) would lead one to suppose that a more extended base might have been obtained, I found, after many careful examinations of the gullies and fissures which intersect it, that some of the concealed fissures run much farther into the Rock than might at first be imagined. The adoption of a much larger base, even had it been otherwise advisable, would therefore have involved some risk of the external ring of stones of the lowest course giving way by the yielding of an unsound part of the outer portion of the Rock to the pressure of the superincumbent mass, and might eventually have led to the destruction of the Tower.
No. 2.
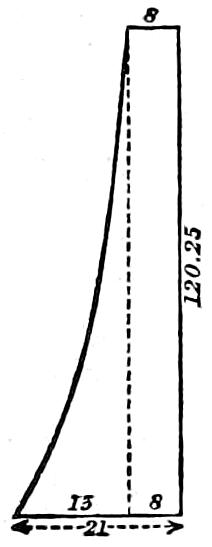
The height of the Pillar having been finally fixed at 138·5 feet, and the radius of the base, at the level of about 4 feet above high water, at 21 feet, I next proceeded to consider the details of its proportions. Of the whole height of 138·5 feet, 18 were to be absorbed in a suitable capital for the Pillar, consisting of a parapet for the Lantern, an abacus, a cavetto, and a belt separating these from the shaft. The internal void I determined should be 12 feet in diameter, as the size most suitable for the reception of the lantern and apparatus; and this, combined with the choice of about 13,000 cubic feet of void already mentioned, fixed the height of the solid frustum at the base of the Tower at about 26 feet above the foundation. Having farther decided that the thinnest part of the walls, immediately under the belt-course which separates the capital from the shaft, should not be less than 2 feet thick, as necessary to give due solidity and strength to the walls, and prevent, by the breadth of the joints, the percolation through the walls of the water which might be furiously dashed against them in storms, I had nothing farther to do but to determine the nature of the line which should connect the extremities of the top and bottom radii of the Pillar. As I had already concluded that this line must, as in the Eddystone and Bell Rock, be[60] a curve line, concave to the sea, I next proceeded to try the effects of various curves traced between these points, in giving a convenient and advantageous disposition of the materials, with regard to both the thickness of the walls and the mass of the solid frustum at the base of the Tower. These two points, as will be better understood by means of the accompanying diagram (No. 2), are separated from each other vertically 120·25 feet, and are horizontally distant from each other 13 feet, which is the excess of the bottom radius over that of the top of the shaft, or the consequent amount of what may be called the aggregate slope of the wall. The solid generated by the revolution of some curve line about the vertical axis of the building then becomes the shaft of the pillar. For this purpose I tried four different curves, the Parabola, Logarithmic, Hyperbola, and Conchoid, figures of which, upon the same scale, will be found in Plate, No. IV., with the position of the centre of gravity, which was carefully calculated, marked on each. The logarithmic curve I at once rejected, from its too near approach to a conic frustum, and the excessive thickness of the walls which such a figure would produce, where the hollow cylindric space for the internal accommodation commences at the level of 26 feet above the base. The parabolic form displeased my eye by the too rapid change of its slope near the base; and I had some difficulty in reconciling myself to the condition of the exterior ring of stones at the base, too much of the outer portion of each stone being left without the advantage of direct pressure from the superincumbent mass of the wall above. The two remaining pillars, derived from the hyperbolic and conchoidal[12][61] frusta, are nearly identical in form; and of these two curves I preferred the former, which gives the most advantageous arrangement of materials, in regard to stability, of all the four forms. This quality of advantageous proportion exists in these forms, in the ratio of the numbers in the last column of the following table:[13] which shews a slight superiority of the Hyperbolic over any of the other forms.
| Hypothetical Towers. |
Height of the Tower in feet. (H.) |
Diameter | Volume of solid Tower in cubic feet. M. |
Distance of centre of Gravity from Base. G. |
HG | Economic Advantage. G.M.G′·M′. |
|
|---|---|---|---|---|---|---|---|
| at Base in feet. |
at Top in feet. |
||||||
| Hyperbolic, | 120 | 42 | 16 | 62,915 | 41·227 | 2·911 | 1·00000 |
| Conchoidal, | 120 | 42 | 16 | 62,984 | 41·336 | 2·903 | 0·99627 |
| Parabolic, | 120 | 42 | 16 | 63,605 | 43·400 | 2·765 | 0·93963 |
| Logarithmic, | 120 | 42 | 16 | 74,742 | 42·460 | 2·826 | 0·81608 |
| Conical, | 120 | 42 | 16 | 84,737 | 43·280 | 2·773 | 0·70725 |
[12] The solid, in this case, would have been formed by the revolution of the interior conchoid of Nicomedes about its directrix; and its co-ordinates were kindly calculated for me by my late revered preceptor, Dr Wallace, Professor of Mathematics in the University of Edinburgh, who employed so many hours of his latter years in labours of kindness among his friends. This act of the Professor was the result of a conversation I had with him on the subject. Before I received his friendly communication, however, I had resolved to adopt the rectangular hyperbola, whose co-ordinates I had myself determined with this view some time before; and when I found that the conchoid and the hyperbola, traced between the two fixed points by means of the calculated co-ordinates, were so nearly coincident, that it was difficult to prevent their running into each other, even when drawn out on a large scale, I determined to adhere to my original purpose of adopting the latter curve as my guide.
[13] The last column of this table is derived as follows:—Assuming that the economic advantage of any proposed tower of given height and diameter at base and top, is inversely as the mass and the height of the centre of gravity above the base, and denoting these quantities by M and G respectively, the fraction 1G·M may be taken as an indication of the economic advantage of the proposed tower. Let 1G′·M′ express the economic advantage of another tower; then the advantage of the second tower, compared to that of the first, taken as unity, will be G·MG′·M′, by which expression, the last column in the table was calculated.
The shaft of the Skerryvore Pillar, accordingly, is a solid, generated by the revolution of a rectangular hyperbola about its asymptote as a vertical axis. Its exact height is 120·25 feet, and[62] its diameter at the base 42 feet, and at the top 16 feet. The ordinates of the curve, at every foot of the height of the column, were carefully determined in feet to three places of decimals; and the Appendix contains a tabular view of the co-ordinates from which the working drawings were made at full size. The first 26 feet of height is a solid frustum, containing about 27,110 cubic feet, and weighing about 1990 tons.[14] Immediately above this level the walls are 9·58 feet thick, whence they gradually decrease throughout the whole height of the shaft, until at the belt they are reduced to 2 feet in thickness. Above the shaft rests a cylindric belt 18 inches deep; and this is surmounted by a cavetto 6 feet high, and having 3 feet of projection. The contour of this cavetto is that resulting from a quadrant of an ellipse revolving about the centre of the tower, with a radius of 8 feet on the level of its transverse axis; and the moulds for this curve were drawn at full size from co-ordinates calculated for the purpose. The cavetto supports an abacus 3 feet deep, the upper surface of which forms the balcony of the tower, and above it rest the parapet-wall and lantern.
[14] At the rate of 13·62 cubic feet of granite to a ton.
It may, perhaps, be not uninteresting to the reader to examine the woodcuts (No. 3), which shew, on one scale, the elevations of the Lighthouses of the Eddystone, the Bell Rock, and the Skerryvore, and exhibit the level of their foundations in relation to high water. They will also serve to give some idea of the proportionate masses of the three buildings. The position of the centre of gravity, as calculated from measurements of the solids, is also marked by a round black dot on each tower; and in the table following, I have given the cubic contents of each of these towers, the height of the centre of gravity above the base and the ratio of that quantity to the height of the tower.
[63]
No. 3.
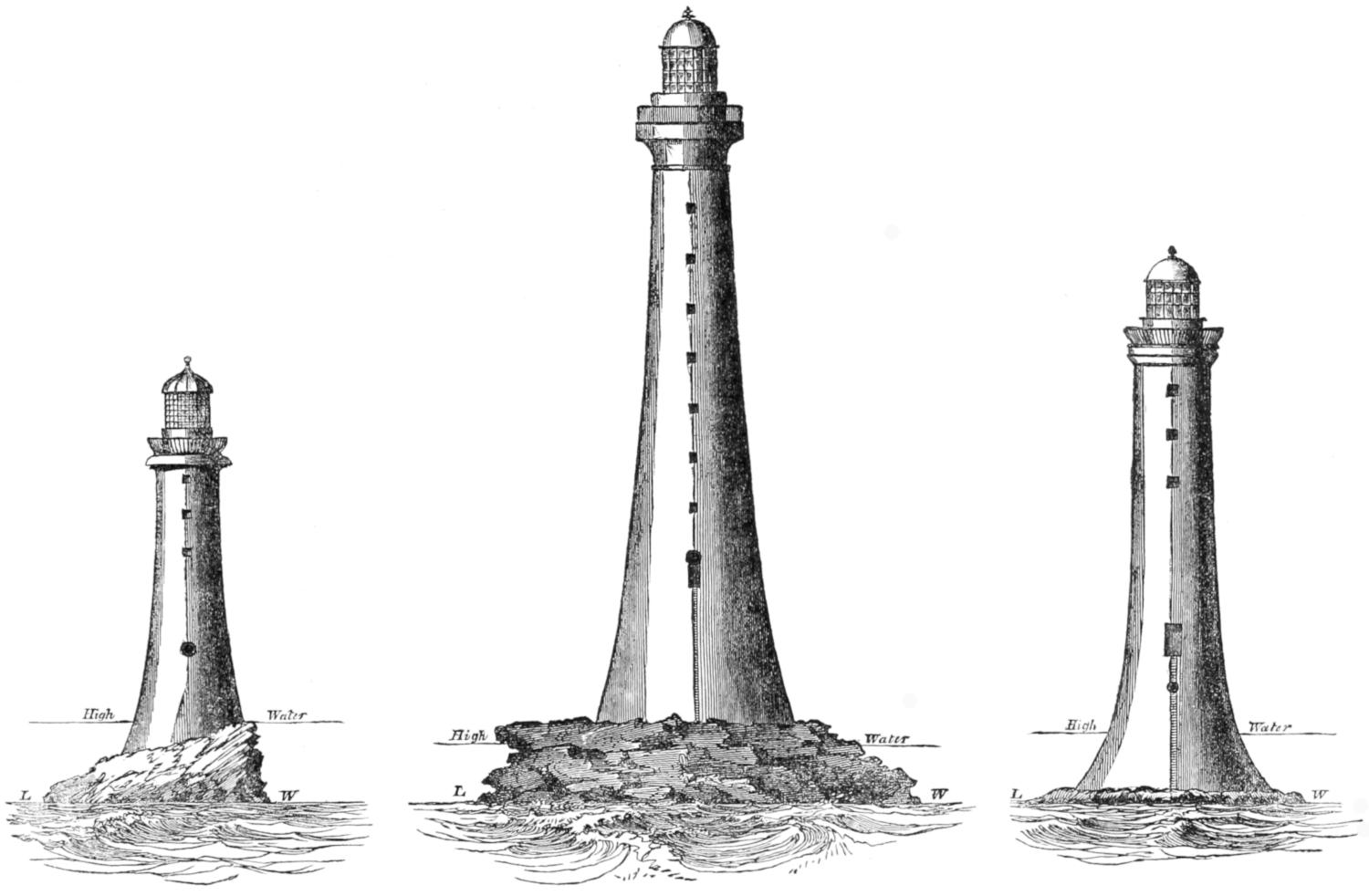
EDDYSTONE.
SKERRYVORE.
BELL ROCK.
| Lighthouse. | Height of Tower above first entire course. (H) |
Contents of Tower. |
Diameter | Distance of centre of gravity in feet from Base. (G) |
HG | |
|---|---|---|---|---|---|---|
| at Base. | at Top. | |||||
| Eddystone, | 68 | 13,343 | 26 | 15 | 15·92 | 4·27 |
| Bell Rock, | 100 | 28,530 | 42 | 15 | 23·59 | 4·24 |
| Skerryvore, | 138·5 | 58,580 | 42 | 16 | 34·95 | 3·96 |
I come now to notice the few subordinate points in which the design of the Skerryvore Tower may be regarded as differing from those of the Eddystone and the Bell Rock. In glancing at the[64] contrasted figures of the three buildings, it will be at once observed that the outline of the Skerryvore approaches more nearly to that of a conic frustum than the other two. To the adoption of this form, various considerations induced me; and these I shall very briefly detail. In the first place, it seemed to me that, in both the Bell Rock and the Eddystone, the thickness of the walls had been reduced to the lowest limits of safety towards the top; and the effects of the sea and wind acting upon a heavy cornice, cause a degree of tremor which I felt satisfied would not occur in a building with thicker walls. The effect of thickening the walls at the top, is, of course, cæteris paribus, to diminish the projection of the base, and thus to produce less concavity of figure, and consequently a nearer approximation to the contour of a conic frustum. I have already stated, that this excess of the bottom radius over that of the top, is in the Skerryvore Tower 13 feet, and that the height of the shaft is 120·25 feet. The quotient resulting from the division of the height by the excess of bottom radius over that at the top is 9·27; and, if the figure had been conical, this number would have given a measure of the slope of the walls throughout. There can be little doubt that the more nearly we approach to the perpendicular, the more fully do the stones at the base receive the effect of the pressure of the superincumbent mass as a means of retaining them in their places, and the more perfectly does this pressure act as a bond of union among the parts of the Tower. This consideration materially weighed with me in making a more near approach to the conic frustum, which, next to the perpendicular wall, must, other circumstances being equal, possess the property of pressing the mass below with a greater weight, and in a more advantageous manner, than a curved outline in which the stones at the base are necessarily farther removed from the line of the vertical pressure of the mass at the top.[15] This vertical[65] pressure operates in preventing any stone being withdrawn from the wall in a manner which, to my mind, is much more satisfactory than an excessive refinement in dovetailing and joggling, which I consider as chiefly useful in the early stages of the progress of a work, when it is exposed to storms, and before the superstructure is raised to such a height as to prevent seas from breaking right over it.
[15] It is most satisfactory to find that the views expressed above, regarding the eligibility of the conical form, seem to have the sanction of the late Dr Thomas Young, who appears to have connected his preference of this form with its greater efficiency as a source of friction among the parts of a building. In his syllabus of Lectures, under the section “Architecture,” he thus speaks: “For a Lighthouse where a great force of wind and water was to be resisted, Mr Smeaton chose a curve convex to the axis. In such a case, the strength depends more on weight than on cohesion, and also in a considerable degree on the friction which is the effect of that weight. Perhaps a cone would be an eligible form.”
If these views be substantially correct, it may not, perhaps, be altogether inadmissible (without, however, venturing to enunciate any general law) to conclude, that, in the three Lighthouses of the Eddystone, the Bell Rock, and the Skerryvore, this source of union among the outer stones of the lower courses must bear some proportion to the numbers 753, 659, and 927, which are the quotients of the height of the column, divided by the difference of the top and bottom radii of the shaft in each case respectively. This consideration seems too important to be entirely overlooked; and I conceive that, by following out this view, I have been enabled to depart with perfect safety from the intricate and elaborate work required for the connection of the materials by means of dovetailing and joggling, which the adoption of a more concave outline (in which the vertical pressure could not have been so advantageously transmitted to the outer stones of the base), would perhaps have rendered advisable. In the case of the Bell Rock, however, whose construction, in regard to this property, is the least advantageous of the three buildings, it must be borne in mind that the Tower is covered to the depth of 15 feet at spring tides, and that this principle of vertical pressure could not have been safely appealed to during the whole time which intervened between the commencement[66] of the building and the attainment of a height sufficient to render it available, which, in a Tower having so great a part submerged, was of necessity much prolonged. The stones were thus exposed to the full effect of heavy seas, at all levels, during two entire winters, and could not therefore have been safely left, without being kept together by numerous ties and dovetails. It also seemed important, in designing that Tower, with reference to the rise of tide, to give its lower part a sloping form, as the least likely to obstruct the free passage of the waves. The outer stones of the lower courses were also selected of unusual length inwards, so as to bring them more under the influence of the vertical pressure of the upper wall.
Before leaving this subject, I may remark, that it is quite possible to construct a Tower of a curved form, in such a manner, that the pressure of the upper part of the pillar shall be distributed to the greatest advantage on every stone, by building the outer walls as inverted arches, so that the section of each stone shall be that of a voussoir, with joints perpendicular to the successive tangents of the curve. This arrangement of the stones is, in fact, practised in sea walls of various kinds, and has even been recommended for circular Towers in an ingenious paper in the Transactions of the Royal Scottish Society of Arts. But in many situations, and at Skerryvore in particular, this mode of transmitting the pressure, so as to throw it perpendicular to the beds of the stones, is inadmissible, as conducing to or involving a greater evil. The evil has already been noticed, and consists in the thrust of the lowest stone (which is of course inclined to the horizon) having a tendency to push out the sides of the Rock on which the Tower is built. This fear, where the Towers are to be placed on small steep rocks or pinnacles, and more especially when these Rocks are traversed by veins nearly vertical, is by no means visionary; and there is good reason to apprehend, that the pressure thus resulting in a line considerably inclined to the plane of cleavage, might throw outwards a thin portion of[67] rock, which, under the more conservative influence of a vertical pressure, might continue to retain its connection with the rest of the Rock unimpaired for ages.
Another method of, in some degree, increasing the resistance of a Sea Tower to a horizontal thrust, if such aid be required, is to give the line of courses a continuous spiral form, instead of building them in successive horizontal layers. Were there reason to fear that the entire dislocation of the building might take place in a plane nearly horizontal, this method seems more calculated to counteract the danger than the use of dowels or joggles passing from the course below to the course above; but, as this is one of the accidents least to be apprehended, there does not seem any good ground for resorting to a mode of structure which would lead to considerable intricacy of workmanship, and would, in practice, be attended with difficulty in obtaining a proper vertical bond or union among the several stones.
The only remaining point, in which the example furnished by the Eddystone and Bell Rock Lighthouses has been at all materially departed from, is (as has already been hinted at by an unavoidable anticipation) the mode of uniting the different parts of the masonry together. In both these Towers the stones were dovetailed throughout the buildings, chiefly (at least in the case of the Bell Rock where the foundation was so much below the tide) with the view of preventing the sea from washing away the courses which might be left exposed to the winter storms before the weight of the superstructure had been brought to bear upon them. In the upper part of the Bell Rock my father also introduced a kind of band joggle, which consists of a flat ribband of stone raised upon the upper bed of one course, and fitting into a corresponding groove cut in the under bed of the course above; and this system of tying the adjoining courses together also forms a chief feature in his design for a Lighthouse on the Wolf Rock.[16] When the[68] great pressure of the superstructure of these Towers, however, and the effect of the mortar are considered, there seems little probability of one course being dislocated, in defiance of the friction resulting from the weight of the column. An impulse sufficient to produce such an effect would tend to overset the whole superstructure from mere deficiency in weight, and in this case the joggle would have little effect. But if joggles be thought necessary for this purpose, the ribband form certainly produces a better arrangement than that of the cubic joggles employed by Smeaton for connecting the adjoining courses of his building together, as the sectional strength of these scattered square joggles is very small compared to the effect of a shock which could be supposed capable of moving the whole mass of a Tower. In the lower parts of the Skerryvore Tower, I entirely dispensed with dovetailing and joggles between the courses, and thus avoided much expensive dressing of materials. The stones were retained in their places during the early progress of the work, chiefly by common diamond joggles, and the courses were temporarily united to each other by wooden treenails, like those used in the Eddystone and Bell Rock. These treenails had split ends, with small wedges of hardwood loosely inserted, which being forced against the bottom of the holes in the course below, into which the treenails were driven, expanded their lower ends until they pressed against the sides of the holes; while their tops were made tight by similar wedges driven into them with a mallet. I have, however, adopted the ribband-joggle in the higher part of the Tower, where the walls begin to get thin in the very same manner as at the Bell Rock, where it was used, partly that it might counteract any tendency to a spreading outwards of the stones, and partly that it might operate as a kind of false joint to exclude the water which, when pressed with great violence against the Tower, is apt to be forced through a straight or plain joint. The stones in the higher courses throughout each ring are also connected at the ends by double dovetailed joggles, which unite the two adjoining stones; and the walls are, besides, tied together[69] at various points by means of the floor stones, which are all connected by dovetails let into large circular stones which form the centres of the floors. I also ventured to leave out the metallic ties at the cornice, which consisted, at the Eddystone, of chains, and, at the Bell Rock, of copper rings. The reasons which induced me to adopt this change I need not here enlarge upon. It is sufficient to state, that I believe I have nearly balanced the forces which would have tended to throw the cornice outwards, had a greater disproportion existed in the weight of the outer and inner parts of the cavetto, and to point out (Plate VII.) that the Lightroom or highest floor occurs, at such a level, as of itself to answer all the ends which metallic ties could have served.
[16] Account of the Bell Rock Lighthouse, Plate XXI.
The hazardous nature of the anchorage, and the consequent difficulty of mooring a vessel in the neighbourhood of the Skerryvore Rock, induced me, from the first, to consider it as a matter of great importance, even at a large expenditure of time and money, to erect Temporary Barrack on Rock. some temporary dwelling on the Rock for the accommodation of the people engaged in the work, with the view of rendering the operations less dependent on the state of the sea, which varied with every wind. So important, indeed, did this object appear to me, that I was at times apt to look upon it as an indispensable step towards ultimate success. That opinion was amply confirmed during our first season’s operations, by the experience of the oft-recurring difficulty of returning to the moorings when driven away by stress of weather, together with the daily risk and loss of time in landing the workmen in small boats, even in weather when they could be profitably occupied if once placed on this small terra firma. With this view, I naturally turned to the same plan which had been adopted at the Bell Rock, where the temporary barrack stood the test of five winters. That structure, which is represented in Plate No. V., and is particularly described in the Appendix to my father’s Account of the Bell Rock Lighthouse, consisted of an open framework of six logs, about 47 feet long and 13 inches square, assembled in such a manner as to form by their union a hexagonal pyramid, on the top of which rested a wooden turret; the whole erection rising to the height of about 60 feet above the rock. This pyramidal framework was strongly trussed and tied; and, being open at the lower part, offered little resistance to the waves. The upper part contained a gallery for keeping various[72] stores and such materials as could not be safely left on the Rock, even in the finest weather; but it was framed of lighter materials, so as to admit of its yielding easily to any extraordinary waves, without involving injury to the principal part of the structure, by offering great resistance to the sea. The turret on the top was in the form of a twelve-sided prism, 12 feet in diameter, and 30 feet high, and was securely attached, by means of the ties and braces shewn in the drawing, to the apex of the pyramid, which entered into the lower part of it. The small space which the turret afforded was, with the utmost economy of room, divided into three storeys, of which the lower was entirely taken up by the kitchen and the bread-store, a great deal of room being occupied by the main beams of the pyramid which passed through its centre. The next storey was subdivided into two chambers, of which one was appropriated to the foreman of the works and the landing-master, while the other was set apart for myself; and the top storey, which was surmounted by a small lantern and ventilator, formed a barrack room, capable of containing 30 people. Of the comforts and discomforts of this habitation I shall at some future time have occasion to speak. I merely draw attention to its erection at present, as an operation, which it was most desirable should precede every other work on the Rock. One of the first proceedings, therefore, was to obtain estimates for the preparation of this log-house, which, in order to avoid loss of time in making adjustments on the Rock, was to be carefully fitted up in the workyard of the contractor before being shipped. Drawings and a specification were accordingly prepared, and submitted to several carpenters in Greenock, who gave in offers for the work; and it was finally commenced in the month of March, by the late Mr John Fleming, who was the successful offerer.
Tools and Machinery. It was also necessary to provide a large assortment of quarriers’ and masons’ tools of every kind; and many cranes, crabs, anchors, mooring buoys and other implements were ordered, according to detailed specifications and drawings. These preparations necessarily occupied the early part of the year 1838.
[73]
From the extent of the foul ground round the Skerryvore, and the absence of good harbours in the neighbourhood, it was foreseen at the outset that the operation of landing about 6000 tons of materials on the Rock could not be accomplished by means of sailing vessels with that degree of certainty or regularity which was desirable, in order to obtain the full benefit of the short working season which the climate of the Western Hebrides affords; and the necessity for providing a Steam Tender for the Works. steam tender was, therefore, generally admitted. It has already been stated, that, in order to avoid the expense attending the building of a vessel for this purpose, application was made at the principal ports of the kingdom, with the view of purchasing a suitable vessel; but, although twenty-four vessels of nearly the required dimensions were offered for sale, not one of them was considered fit for such a service, the great majority being light craft, such as are generally used in river and port navigation. It was therefore found necessary to build a steamer; for which purpose, specifications and drawings were prepared, and after receiving various tenders from respectable parties, a contract was entered into with Messrs Menzies and Sons, shipbuilders, and Messrs J. B. Maxton and Co., engineers, both of Leith, for building a steamer of 150 tons, with two engines of 30 horse power each.
The use of a steamer, at the very outset of the works, would doubtless have proved of the greatest service in the erection of the barrack on the Rock, and would have materially lightened our cares and toils; but I am not sure that I should have acquired so thorough an acquaintance with the difficulties and dangers of the Skerryvore, or that I should have been so well prepared for all the obstacles that presented themselves in the after parts of the work, had the first season’s operations been conducted under those advantages which are always derived from the use of steam-power. As it was, we had much to bear from the smallness of the Lighthouse Tender, named the Pharos, a vessel of 36 tons, new register, which was all the regular shipping attendance we possessed during this first season; and the inconvenience arising from her heavy[74] pitching, was, to landsmen, by no means the least evil to be endured. But the frequent loss of opportunities, of which we might easily have availed ourselves, if we had possessed the command of steam-power, and the danger and difficulty of managing a sailing vessel in the foul ground near the Rock, and between it and Tyree, were, perhaps, even more felt by the seamen than by the landsmen; and if the experience of a single year’s work can form any ground for an estimate of the length of time required for building the Skerryvore Lighthouse, with a sailing vessel, I should say, we must still (even in 1845) have been engaged in the masonry part of the work, which was finished on the 25th July 1842.
About the middle of April, arrangements were made with Mr Charles Neilson, a builder in Aberdeen, to select granite masons for the works at the Skerryvore, as it was expected that the operation of dressing stones for the Tower would be begun in the ensuing summer; and it was also obvious, that their services would be required in excavating seats for the supports of the Barrack-house on the Rock. Employment and Wages of Workmen. Masons were accordingly selected, and engaged on the terms stated in the following letter to Mr James Scott, the Foreman, who was sent to Aberdeen to assist in choosing the men:—“Although it is difficult to fix the precise number of men who may be required, during the progress of the works, as this must, in some measure, depend upon the produce of the quarries at Hynish, and of those to be opened in Mull, you may, in the mean time, engage thirty masons or stone-cutters, twelve quarriers, and three or four smiths, for two years of certain employment. With regard to the rate of wages to be paid to the men, this will, in some measure, depend upon the demand for the season at Aberdeen; it is, at all events, expected, that they will on no account exceed the rate of 3s. 10d. per day for masons, and 2s. 6d. per day for quarriers, as paid last season during the long day, or from the 1st of February till 31st of October; and for the short day during the remaining three months, 3s. for the masons, and 2s. for the quarriers, from 1st November till 31st January.
“It is intended that subsistence money shall be paid to such of[75] the families or relatives of the workmen as may require it; and that their wages shall be fully settled monthly, deducting the subsistence money advanced to their relatives. A Store will be kept at the works by the Lighthouse Board, from which provisions will be served out at stated periods, to be fixed by the storekeeper; and these provisions shall be sold to the workmen at the cost prices at which such stores are laid in. Barrack accommodation or lodgings, with cooking, will also, as formerly, be allowed to the men free of expense.”
Progress of the outfit for the season’s operations. Early in the month of May the preparation of the wooden barrack for the Rock had been completed, and the whole had been set up in the workyard at Greenock; and when I visited it for the last time about the 5th of that month, I found it all ready for shipment, excepting some additional iron ties, which I ordered for securing the turret to the top of the pyramid, which were to be applied at the level of the floor of the upper or barrack-room storey. I also found that the moorings, including the mushroom anchors and chains, and the workyard materials, consisting of several cranes, trucks, a janker for the transport of timber, and a Woolwich sling-cart for carrying stones to the various sheds, were in the course of preparation. A large assortment of masons’ and quarriers’ tools was at the same time ready for shipment at Aberdeen. Early in June, a vessel called the Duke of Montrose was chartered to carry coals to Tyree, both for household purposes and for the work; and two small portable smiths’ forges were prepared for use on the Rock.
In providing the means of efficiently carrying on so many complicated operations in a situation so difficult and remote, it is impossible, even with the greatest foresight, to avoid omissions; while delay of a most injurious kind may result from very trivial wants. Even the omission of a handful of sand, or a piece of clay, might effectually stop for a season the progress of plans, in the maturing of which hundreds of pounds had been expended. Accordingly, although I had bestowed all the forethought which I could give to the various details of the preparation for the season (of[76] which I found it absolutely indispensable to be personally aware, even to the extent of the cooking dishes), new wants were continually springing up, and new delays occasioned, so that it was not until the evening of the 23d of June that I could Embark for Skerryvore. embark at Tobermory in the Pharos Lighthouse Tender, commanded by Mr Thomas Macurich, with all the requisites on board for commencing the season’s operations. Next morning we moored off Hynish Point about three o’clock, and, from the roughness of the passage, were not unwilling to land at that early hour. Here I found that Mr Scott, the foreman of the workyard, had, notwithstanding the unworkable nature of the Rock, more particularly afterwards noticed, procured about sixty fine blocks of gneiss, as the produce of the Tyree quarries, which had been wrought for upwards of 15 months; and had at the same time completed the masonry of a range of buildings for stores and barracks, capable of containing upwards of 100 men, and had built about 100 feet in length of a landing-pier, reaching nearly to low-water mark. A magazine for gunpowder, of which a considerable stock was required for quarrying purposes, had also been built; and a piece of garden ground had been inclosed and stocked for the use of the people to be employed at the works. Measures had also been taken for inclosing the ground, which had been feued by the Board from the Duke of Argyll. This day being Sunday, nothing was done at Hynish, and we waited until next morning before sailing for the Rock.
25th June.—Sailed in the Pharos from Hynish Bay this morning about six, with Mr Scott, the foreman of the workyard, and one or two masons on board; but, having a foul wind during the early part of the day, and the weather falling afterwards calm, it was not until three in the morning of the 26th that we reached the Rock.
26th June.—Our first step was to Lay down Moorings, and try to land on the Rock.lay down moorings for the tender as near the Rock as seemed to be consistent with safety. The position chosen by Mr Macurich, who commanded the vessel, was to the S.S.E. of the Rock, about a quarter of a mile off, and in 13 fathoms water, on an irregular rocky bottom. About half-past[77] five I attempted a landing on the Rock, but there was a great deal too much sea. The vessel was pitching the bowsprit under at her moorings, and the surf broke into the creek where landings are generally made, in such a manner as to render it quite impossible to get near the Rock. After hanging on our oars in the boat for nearly an hour, in the hope of a smooth lull between the heavy seas, we returned to the vessel, and, as the wind still freshened from the S.E., we reefed the mainsail and set the first jib, and steered for the Mull shores, where, about ten at night, we came to an anchor in Loch Loich, not far from the Island of Iona.
27th June.—Next day also being unsuitable for attempting to reach the Skerryvore, the vessel lay in North Bay, and the early part of the day was spent in a careful examination of the granite Rocks of the district called Driven to Mull. Ross of Mull, with the view of establishing quarries there; as our experience of the unsatisfactoriness of working the Tyree quarries during fifteen months had frequently led me to anticipate the necessity of soon seeking a supply of materials in some other quarter. In this district an almost inexhaustible supply of flesh-coloured granite was found, not certainly of the hardest description, but singularly equal and homogeneous in its texture. I therefore made a general survey of the neighbouring localities, with a view to select the best position for opening quarries and establishing a landing place or wharf for shipping the materials, as well as for erecting barracks for the workmen. In the afternoon, I embarked at the call of Mr Macurich, to attempt another landing on the Skerryvore; but as the wind soon fell calm, we did very little good until evening, when some progress was made in stretching across towards the Rock.
28th June.—At nine this morning, we reached our moorings at the Rock, but there was still so much surf that a landing could not be attempted till mid-day, when I went with Mr Macurich in the boat, and with some difficulty contrived to spring on the Rock, after which the boat returned to the vessel for the rest of the party. While left alone on this sea-beaten Rock, on which I had[78] landed with so much difficulty, and as I watched the waves, of which every succeeding one seemed to rise higher than the last, the idea was for a few minutes forcibly impressed on my mind, that it might, probably, be found impracticable to remove me from the Rock, and I could not avoid indulging in those unaccountable fancies which lead men to speculate with something like pleasure upon the horrors of their seemingly impending fate. These reflections were rendered more impressive by the thought that many human beings must have perished amongst those rocks. A consideration, however, of the rarity of an opportunity of landing on the Rock, and the necessary shortness of our stay, soon recalled me to my duty, and before the boat returned with a few of the workmen, I had projected some arrangements as to the first step to be taken in erecting the framework of the barrack-house. The second landing was more easily effected, as the tide had fallen, and the landing-place was more sheltered, First day’s work on the Rock. so that we were the more emboldened to make a fair commencement of operations. It was a day of great bustle and interest, the work consisting in chalking out and marking on the Rock with paint, the sites of the Lighthouse-Tower, and the wooden barrack, and the positions for cranes, crabs, and ring-bolts for guys and other tackling, as well as ascertaining such dimensions as would enable me at once to proceed to fit up the log-house, or barrack, at our next landing. In that way, we spent four hours on the Rock, much to the annoyance of the seals and the innumerable sea-fowl, which we drove from their favourite haunts. During the whole day, the sun had great power; and the smell from the cast-away feathers and the soil of the sea-fowl was extremely disagreeable. I was amazed to find that those animals should select, as their place of repose, a rock in the Atlantic, intersected by deep gullies which are never dry, with only one pinnacle, about 5 feet in diameter, raised about 16 feet above the sea. while the greater part is only 5 feet above high water. Yet, in a crevice of this Rock, I found an egg resting on a few downy feathers, which the first wave must have infallibly washed[79] away! After the day’s work on the Rock, we sailed for Tyree, but did not reach the workyard till next morning at nine; and a long day of bustle and hurry was spent there in preparing provisions, timber, ring-bolts, chains and all sorts of tackling for the operations connected with the erection of the barrack on the Rock. On the evening of the 30th June, I sailed for Greenock, whence I trusted soon to return to the Skerryvore with the whole of the materials, to commence operations.
It seldom happens that human expectations are fully realised, especially in matters which excite a strong interest in the mind, and thus lead one to desire a more rapid progress than usual. But this is peculiarly true in all arrangements which depend on the co-operation of many persons; and so I experienced on my visit to Greenock and Glasgow, where I had given orders for Shipment of all the materials at Glasgow and Greenock. shipping all the machinery and apparatus required for carrying on the works, such as cranes, trucks, boats, blocks and tackle, anchors, coals, grindstones, stucco, pavement, mats and fascines for blasting, clay for puddling, shear-poles, and innumerable small utensils, some of no great value, but all necessary to the success of the work. The great bulk of those materials were despatched by a vessel called the New Leven, and part by the Mary Clark, on the 24th July; but it was not until the 30th that the Pharos Lighthouse tender was fully loaded, on the morning of which day I again embarked at Greenock for the Skerryvore Rock. The weather proving somewhat unfavourable, we were forced (being very heavily laden) to pass through the Crinan Canal, instead of going round the Mull of Kintyre, so that it was not till the morning of the 4th August that we landed at Reach Tyree. Hynish, in Tyree. Here I found some farther progress had been made in building the barracks for the men, some of the houses being already roofed and slated. The quarries, too, had turned out stones sufficient for about four of the lowest courses of the Tower, a quantity which might be estimated at about 7920 cubic feet. Next day (August 5th), the wind blowing strong from the S.S.W., we were forced to leave Hynish Bay, Driven to Mull. and retreat before a very heavy sea to Tobermory. We immediately sailed again,[80] and made for Loch Erin, a small creek in the Island of Coll, as being nearer to Hynish and better adapted for enabling us to take advantage of any sudden improvement in the weather. On our arrival at this singular natural haven, at nine in the evening, I was glad to find the New Leven, before mentioned as having loaded materials at Greenock lying already there, waiting a favourable change of wind. Next morning we weighed anchor, Return to Tyree. and sailed along with that vessel for Hynish, where she was immediately discharged of her cargo, which was chiefly intended for the workyard there, and took in materials for the erection of the barrack on the Skerryvore Rock.
7th August.—We this morning took on board various tools and implements for the Rock, together with workmen to the number of four carpenters, sixteen masons and quarriers, and a smith, along with Mr George Middlemiss, as foreman. Having sailed with a northerly wind, we made a landing about noon, First good day’s work on the Rock. and had what may be called our first entire day of work on the Rock. Our work was by no means easy, as we had to erect shear-poles and fix crabs for landing the materials, and to lash every article that was landed, with great care down to ring-bolts on the Rock, which a few of the masons were fixing, while the rest of the people were discharging the vessel. All this was attended with a good deal of trouble, and it required my constant attention to keep everything going on in a fair train, so as to prevent one party of workmen requiring to wait for another; but, after eight hours of very hard work, I had the satisfaction of seeing all the materials which had been landed left in a secure state. The extreme smoothness of the surface of the Rock greatly impeded the landing of materials; for as yet we had no tramways on which wheeled trucks could be moved, and the transport by hand of heavy materials over so irregular and slippery a surface was attended with considerable danger. A short trial was this day made of boring one of the holes for the stancheons or bats, by which the timbers of the Barrack were to be secured to the Rock; and I found, that with a jumper of 3¹⁄₂ inches diameter, a depth of about 3 inches was bored[81] in one hour. The commencement of the operations involved much labour and considerable discomfort; but it invariably happened throughout the work, that in spite of all the fatigue and privation attending a day’s work on this unsheltered Rock, the landsmen were for the most part sorry to exchange it for the ship, which rolled so heavily as to leave few free from sea-sickness, and to deprive most of the workmen of sleep at night, even after their unusually great exertions during the day.
On leaving the Rock at night we had the greatest difficulty in boarding the Pharos with two boats containing upwards of thirty-two persons, as the vessel rolled so heavily, that there was great danger of the boats being thrown right upon her deck. Next morning (8th August) we landed, with some sea running, about nine o’clock, before which hour it was impracticable, owing to the surf in the landing creek. Our first work was to prepare the tackling for landing the heavy materials from the New Leven, which came up about eleven o’clock, and was made fast by a warp to the Pharos. We next took means for fixing the smith’s forge on the Rock and preparing the fixtures for the crab, which stood on the point of rock to the westward (see Plate III.), and served chiefly for raising the beams of the log-house into their places. The greater part of the day, till half-past eight in the evening (when it became dark), was spent in lining off with accuracy the site of the supports of the wooden barrack, and in landing and fixing by strong lashings to the Rock, all the principal timbers and iron fixtures. The spot in which the framework of the first barrack was placed, will be seen by reference to Plate III. The Rock was at this place a good deal lower than the site afterwards adopted for the barrack. The high water of spring-tides rose 2¹⁄₂ feet upon the legs or main beams; but this site had many advantages, as it left more room for operations at or near the Tower itself than could have been obtained in any other position.
We also made some progress in erecting a wooden shed round the smith’s forge, to protect him and his fire from the wind and[82] the spray of the sea. As we left the Rock in the boats, speculating on the prospect of getting the whole of the materials discharged in the course of next day, it was remarked that the northern sky was very clear, and that the wind had entirely fallen. The great and sudden stillness of the air, which permitted every ripple on the ocean to be heard, was regarded by Mr Macurich and the seamen generally, as the forerunner of a change; and the moon, which rose red and fiery, confirmed their fears of a gale. Nor were they wrong in their forebodings. Sudden gale, and great peril to the vessels.About midnight there was a stiff breeze from the S.E., which induced the master of the New Leven to hoist sail, cast loose from us, and run; and had not the seaman on watch on the deck of the Pharos fallen asleep in consequence of excessive fatigue, there can be little doubt we should have been at once called to follow her example, if, indeed, we had not led the way. No sooner, however, did Mr Macurich become aware of the state of the wind, which was blowing very strong at S.S.E. right into the landing place, than he roused me about two o’clock. At this time there was a very heavy sea; the little vessel was pitching her forecastle under, and we had to contend with a strong tide combined with the wind against us in working clear of the Rock, from which our moorings were not more than a quarter of a mile to windward; while from the place where we lay, half of the horizon was foul ground, all lying to our leeward. We soon set sail, but in vain tried to weather the sunk rock Bo-Rhua, whose large black mass (after having imagined ourselves past it) we discovered encircled by a wreath of white foam within less than a cable’s length of us. The heavy seas we encountered had greatly deceived us as to our progress, and thick blinding showers of rain made it difficult to see far beyond the vessel’s head. Such was the precarious and dangerous position of the vessel, that had an attempt been made to tack her amidst the surf which came rolling off the Rock, she would most probably have missed stays, the consequence of which would have been the inevitable loss of the vessel and of every soul on board. In this dilemma[83] we were obliged to resort to a less dangerous expedient, by wearing the ship and running her through the narrow passage between Bo-Rhua and the sunk rocks, about 300 yards to the W.N.W. of it, although this was a most hazardous attempt, as we had then little or no knowledge of that dangerous and intricate passage. A more anxious night I never spent; there being upwards of thirty people on board, with the prospect, during several hours, of the vessel striking every minute. And here I must award due praise to Mr Macurich for the coolness and intrepidity which he on this occasion displayed, and the calmness with which he gave his orders to the crew; and as I stood in the companion, telling him the time at intervals of five minutes, so as to enable him the better to judge of the vessel’s way through the water, I could not but remark the necessity for silence on the part of the master of a vessel in cases of difficulty. The workmen were told to be getting ready for landing, but we did not make them aware of the full extent of the danger; and to avoid confusion, they were not permitted to come on deck. We had no sooner cleared the sunk rocks already alluded to, than we were in fear of the great reef of Boinshly, and the heavy seas which were breaking over the foul ground all round it. In this way we spent a night of almost uninterrupted anxiety until daylight, and at eight in the morning Reach Hynish in safety. we came to the moorings in Hynish Bay, after a hard struggle against wind and tide and a very heavy sea, which made us hang dead a long time off Hynish Point. At one time I feared we should have been forced, as I had been, when returning from my first unsuccessful and discouraging attempt to land on the Skerryvore in 1836, to go round the west side of Tyree and Coll, which is a very foul coast; and when we did round Hynish Point, it was almost at the expense of our boat, which the heavy sea had nearly swept away from us. After all this anxiety about our safety and discomfort from rain, wind, and spray, during five or six hours, we were not sorry to set foot even on the wild shores of Tyree; and I trust there were none who did not gratefully acknowledge the protecting care of Almighty God, in preserving us through such peril.
[84]
Detained by bad weather four days at Hynish. It was not until Monday the 13th that a landing was again effected on the rock, as the wind continued to blow strongly from the south; and the intervening four days were spent in Hynish Bay, landing in the morning, and again returning to the vessel in the evening. During this time I was engaged in making drawings of some of the lower courses of the Lighthouse Tower, with a view to fix finally upon dimensions, from which working drawings and wooden moulds for cutting the stones could be made. The only alleviation of my impatience at being detained at Hynish was the satisfaction of seeing some 20 feet of the pier founded at low water. Late in the evening of the 13th August we again landed on the Rock, when we found time, before dark, to complete the fixture of the smith’s forge, which I had been forced to leave unfinished. Even the short period of work this evening was curtailed by a very heavy shower, which drenched us to the skin—a great evil, where there are many people to be accommodated in a small vessel, without room for much spare clothing, or the means of getting any thing quickly dried. Return to the Rock, and have six days of good weather. After this we had an uninterrupted tract of good weather for six days; and as we landed every morning at four o’clock, and remained on the Rock until eight, taking only half an hour for breakfast, and the same time for dinner, we had thus the work of twenty-eight persons for about ninety hours.
Erection of the Pyramid of the wooden Barrack. After carefully setting out the radial directions in which the six legs, or main beams were to stand, our next step was to lay off their approximate distances from the centre of the Barrack, and to clear a space in the solid Rock of sufficient extent to admit of adjusting the exact positions of the bats before boring the holes. This operation involved the necessity of blasting parts of the Rock by very small shots, the bores being about 1¹⁄₂ inch diameter, and 15 inches in depth, and so directed as to have the effect of throwing off a thin superficial crust without shaking the solid part below. The materials thus quarried in forming the seats for each post were thrown, by means of tackle, into the deepest pools, to prevent their being driven by the sea against the timbers of the barrack, and so injuring them.
[85]
No. 4.
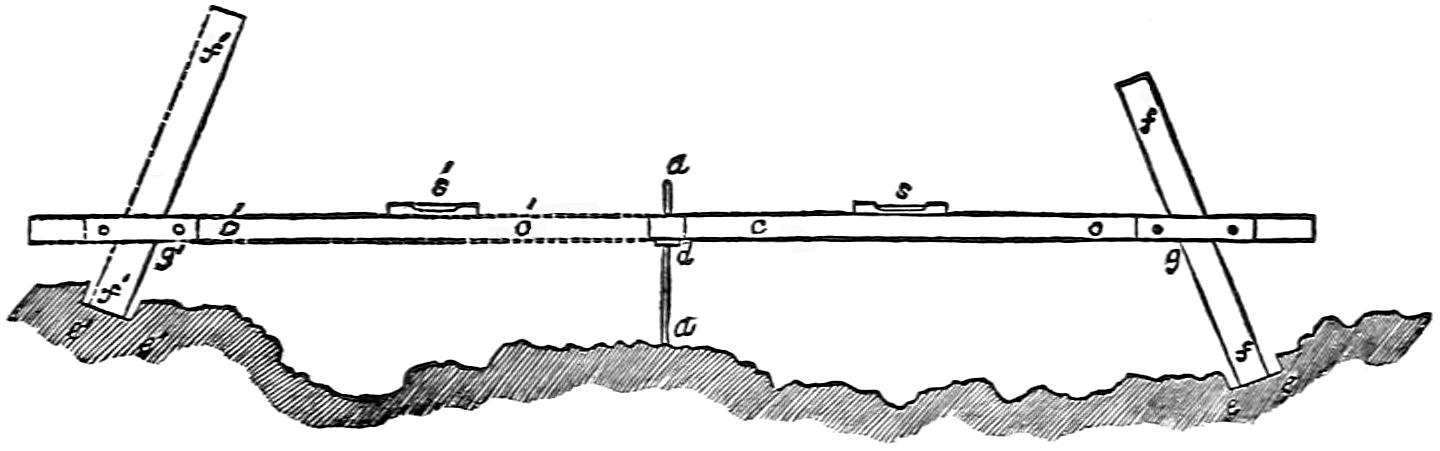
No. 5.
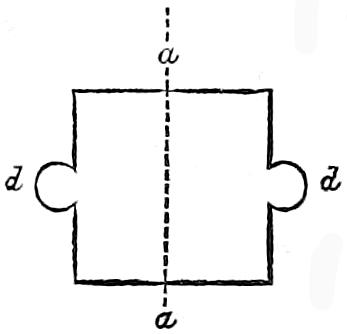
Mode of determining the length of the Beams, and the sites for their fixtures. For ascertaining the exact length of each of the six beams, which formed by their union a pyramid of about 21° 30′ of inclination, and, at the same time, for determining its exact place, in reference to the centre of the hexagon, both of which elements necessarily varied with the level of the irregular surface of the Rock, I used the following simple arrangement:—Each beam being of the greatest length that could be required, the level and distance from the centre were ascertained for the longest beam, which, of course, had the lowest seat or rest, by means of a wooden frame, shewn in the diagram (No. 4), in which a a is a vertical rod of iron firmly batted into the rock, so as to coincide with the centre of the pyramid to be formed by the main beams, and of sufficient length to exceed the greatest variation of level between the different points where the beams are likely to stand; c c is a horizontal board which can be freely turned about a a horizontally, and resting upon a small shoulder d, and which is equal in length to the radius of the hexagon, on the horizontal plane at the level of the lowest beam. On this board is a spirit-level s, which regulates its horizontality; e e is the approximate position of the lower end of the beam; f f is a pitched board, representing the section of the permanent beam, on a vertical plane passing through the axis of the pyramid, and also shewing its inclination towards the centre of the pyramid. As this pitched board is capable of being moved up or down by sliding through a groove at g, it may be successively applied to the rough surface at e e in the course of cutting it down, and thus be made truly to represent the position of the beam, and, at the same time, give the[86] inclination of the surface e e, which must be at right angles to the axis of the beam f f. In this way, by repeated trials, the surface was truly dressed to its proper inclination, and the length ascertained which required to be cut from the beam, so as to make it rest on that surface when in its true position. Hence, also, in the case of all the other beams, the length which the pitch-board f f was moved upwards through the groove g, beyond the level c c, indicated the quantity to be cut from the end of any given beam.[17] The surface of the Rock, dressed for the seat of the beam, being thus brought to its proper inclination, the sliding-board correctly set and the centre line a a of the beam carefully marked on the Rock, a square board (see fig. No. 5) representing the cross section of one of the beams, was then put down at the proper distance, so as to cover the space indicated by the pitch-board as the site of the beam, and with its centre coinciding with the radius already traced on the dressed seat or bed. When so placed, the small round knobs, or ears, d d (No. 5) on this board, shewed the position of the holes to be bored for the bats or side fixtures, which, as afterwards shewn in figure (No. 8, p. 88), spread outwards from the axis of the beam, and thus formed a kind of dovetail. In order to make the holes capable of receiving the bats and, at the same time, embracing the timbers of the barrack, a quoin of wood (Nos. 6 and 7) e, was put down, with bevelled faces or grooves g, cut in it for directing the motion of the jumper or boring iron i, thus:—
No. 6.
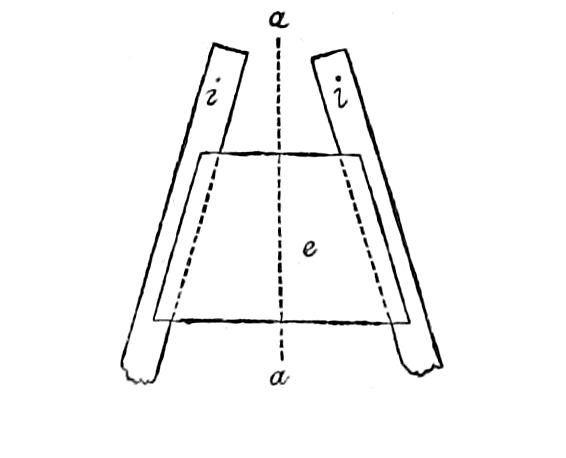
No. 7.
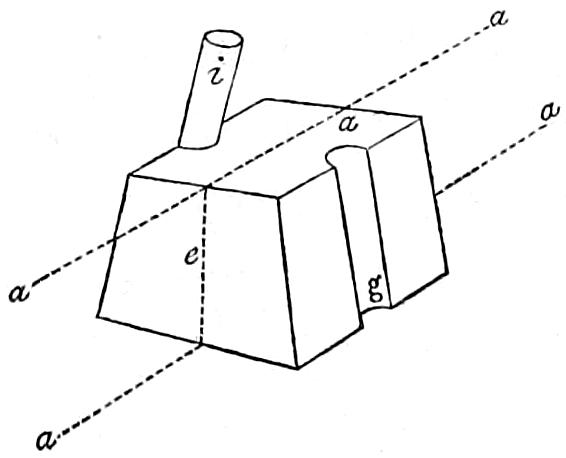
[87]
These holes were bored with jumpers, 3¹⁄₂ inches in diameter, and were sunk 2 feet deep in the rock. The boring of each hole took upwards of eight hours, in consequence of the hardness of the material, which is gneiss, a stone considerably more difficult to bore than even the granite of Aberdeenshire. The bats or stancheons, although very accurately forged, were occasionally found not to fit truly, owing to unavoidable twists in the holes, which arose from dries or veins in the Rock crossing the line of the hole, and thus disturbing the motion of the jumper. This gave us much trouble, and shewed that, had we determined, as I at first contemplated, to cut a lewis-hole, swelling towards the base, the work would have been almost impracticable. The mode which I had proposed for executing this operation was to bore a number of very small holes, inclined at the proper angle, all round the outside of this lewis chamber, and then to cut out between them; but this, as our after experience in cutting the foundation of the Tower proved, would have occupied an extent of time which we should have been very unwilling to bestow upon a merely temporary erection like the wooden barrack. Even as it was, and with all the retrenchments that could be safely adopted, the preparation of the seats for the six outer or main beams, and those for the six inner braces, employed twelve men for four days.
[17] The accented letters e′, c′, f′, g′, o′, s′, in the figure (No. 4), page 85, denote the various parts of the gauging-rule, when applied to the beam, opposite that to which the letters e, c, f, g, o, s, in the text, refer.
No. 8.
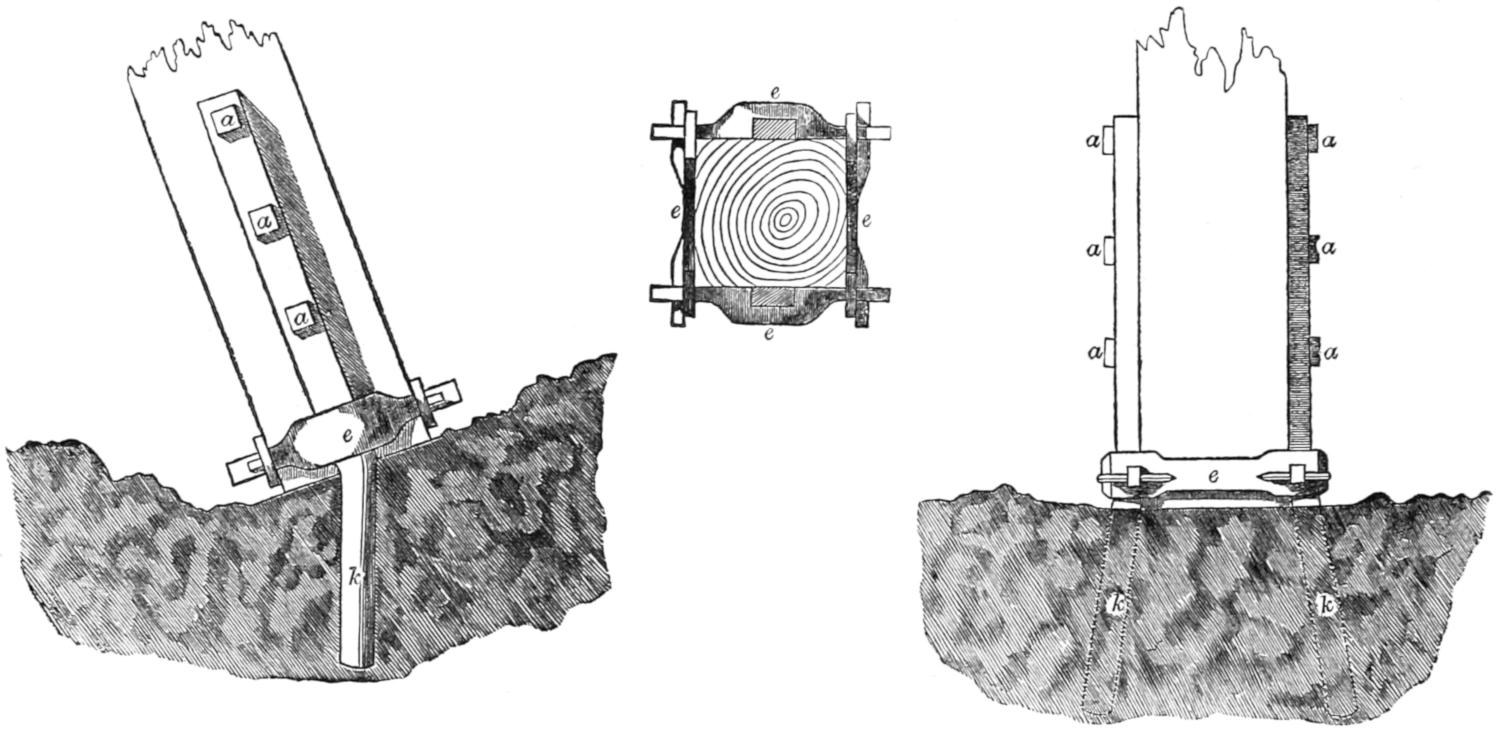
After the seats for the timbers had been dressed in this manner, the carpenters were employed cutting the beams to their respective lengths, the piece to be cut off being measured, as already stated, by the length through which the sliding-board f f (No. 4, p. 85) had been raised above its position on the level platform on which the pyramid had been erected in the workyard at Greenock. At the same time, the stancheons (k k) in the figure (No. 8, p. 88), and the glands or collars e e (in figure No. 8), were let into grooves in the beam, and the holes admitting the screwed bolts a a, to pass through the two stancheons and the beam between them, were bored with an auger, and widened with a red hot iron. The tops of the beams b b (see fig. No. 9), having been already fitted in the workyard at[88] Greenock, so as to meet a hexagonal quoin of hardwood e, round which they were assembled as shewn in the figure (No. 9), straps of iron d d, were made to pass over the top of the whole, and were secured to the beams with bolts, and a spike at a was driven into the centre to wedge the timbers tightly up, so as to fill a ring which embraced the exterior of the whole. It was obvious, that if the sliding-board (described on p. 85) had indicated the true inclination of the seat on the Rock for the end of the beam to rest on,[89] as well as its radial distance from the centre of the pyramid and the corresponding length of the beams, the top of each beam must necessarily meet in its exact place around the central hexagonal quoin. The operation of determining the positions and lengths of such beams on a rugged rock, and placing them with the accuracy requisite, to insure their mitering truly at the top, was attended with a good deal of trouble; and I have judged it advisable to give these details, as they may prove useful to others who may have a similar work in hand.
No. 9.
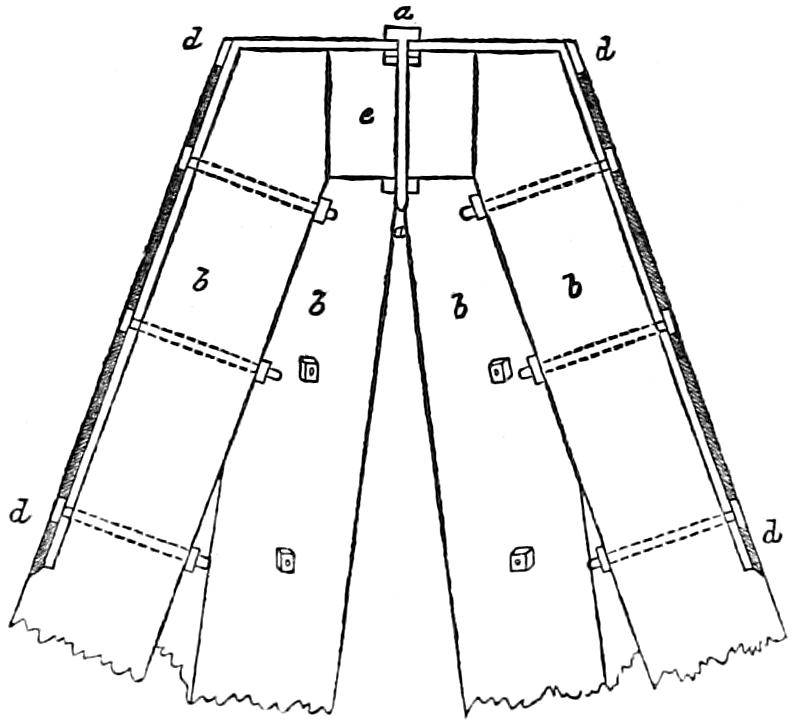
After a good deal of trouble, owing to the lowness of the Rock and the smallness of its surface, the six main beams, each nearly 50 feet long, were raised on end by means of shear-poles, and the iron straps which passed over the top of them, and the ring which embraced the whole so as to secure them at the top, were fixed with much care. The temporary guys were removed on the afternoon of the 18th August. A plummet suspended from the centre of the quoin, after all the six beams were in their places and the stancheons had been run up with lead, came within half-an-inch of the centre bar, which was about 40 feet below the point of suspension, thus indicating an angular deviation of less than 4′. This is a very good approximation, under all the circumstances with which we had to contend; and it is chiefly to be imputed to the very accurate measures pursued in the workyard of the contractor at Greenock, by Mr George Middlemiss, foreman of the carpenters (who then acted as superintendent of the contract works), and whose intelligence and zeal made him, at all times, able and ready to do full justice to all my suggestions for incurring as little loss of time on the Rock as possible. The operation of fixing these six beams, which formed, by their union, a hexagonal pyramid of about 44 feet high, and about 34 feet in diameter at the base, occupied only six days, including the cutting of the seats and the boring of the holes in the Rock. Much labour and time were consumed in the mere moving of beams, each weighing about 13 cwt., over the rugged surface of the Rock, for which purpose we[90] could only use a small set of shear-poles, with crabs and blocks, and tackle purchase; and it sometimes happened, that merely for the purpose of moving a beam, it was necessary to place a special ring-bolt for holding a snatch-block for a few minutes, in spite of all the care and forethought which had been bestowed, in selecting the most advantageous positions for placing them, before the work of raising the beam was begun. Nor was the necessity for securing every loose material by means of lashings to the Rock, before leaving for the night, an insignificant source of delay; for we were sometimes forced by the waves or the darkness, which drove us from our work, to lower a beam which was just ready for being fixed and to replace it in a safe situation.
Pyramid completed. On Saturday the 18th August, the pyramid having been successfully erected, the men were busied for two hours, before embarking for the vessel, in collecting and lashing all the loose materials to the Rock, for the sky gave some indications of a change. As we took to the boats, I looked at the result of our labours with some satisfaction, not unmingled with gratitude.
During the week, while we had been engaged in fitting up the main timbers of the barrack, the weather had been very fine; and except the long hours of toil and the sea-sickness on board the vessel, there was nothing to complain of; Mode of living while erecting the Barrack. but the economy of our life while moored for days off the Rock, was somewhat singular. We landed at four o’clock every morning to commence work, and generally breakfasted on the Rock at eight, at which time the boat arrived with large pitchers of tea, bags of biscuit, and canteens of beef. Breakfast was despatched in half an hour and work again resumed, till about two o’clock, which hour brought the dinner, differing in its materials from breakfast only in the addition of a thick pottage of vegetables, and the substitution of beer for tea. Dinner occupied no longer time than breakfast, and like it, was succeeded by another season of toil, which lasted until eight and sometimes till nine o’clock, when it was so dark that we could scarcely scramble to the boats, and were often[91] glad to avail ourselves of all the assistance we could obtain from an occasional flash of a lantern and from following the voices. Once on the deck of the little tender and the boats hoisted in, the materials of breakfast were again produced under the name of supper; but the heaving of the vessel damped the animation which attended the meals on the Rock, and destroyed the appetite of the men, who, with few exceptions, were so little sea-worthy as to prefer messing on the Rock even during rain, to facing the closeness of the forecastle. As I generally retired to the cabin to write up my notes, when that was practicable, and to wait the arrival of my own refection, I was sometimes considerably amused by the regularity with which the men chose their mess-masters, and the desire which some displayed for the important duties of carving and distributing the rations. Even the short time that could be snatched from the half-hour’s interval at dinner, was generally devoted to a nap; and the amount of hard labour and long exposure to the sun, which could hardly be reckoned at less than 16 hours a-day, prevented much conversation over supper: yet, in many, the love of controversy is so deeply rooted, that I have often, from my small cabin, overheard the political topics of the day, with regard to Church and State, very gravely discussed on deck, over a pipe of tobacco. Perhaps the great heat below, where upwards of twenty people were confined, might in some measure account for this wakefulness on board the Tender.
One beautiful morning, during our stay of six days at the Rock, we had a visit from Shoals of Medusæ seen. a shoal of small fish, whose novel appearance made me take them for a fleet of some species of Nautilus. Those animals came in such numbers, that the pale blue silky membranes or sails, which wafted them before a gentle breeze over the glassy surface of the ocean, literally covered the water as far as we could see. One of those animals I sent in a small phial to my friend, Professor Fleming, then of King’s College, Aberdeen, who assigns to it the Linnean name of Medusa velilla, and says it is noticed by Dr Walker and Mr Pennant, as a native of Scotland.
[92]
The threatening of the previous night was fully verified by the succeeding Sunday morning, as a strong southerly wind with heavy showers, forced us to part from our moorings at the Rock at break of day, and make sail for Hynish Bay, where we anchored at seven. On Monday I landed at Hynish; but as the wind, which had increased to a strong gale, was still rising and inclining more to E., Mr Macurich summoned me to the boat, when, with much difficulty, and at the expense of shipping several seas, we reached the vessel which was pitching the bowsprit under. Driven by a gale to Mull. This soon forced us to run for the Sound of Mull, where we were detained until Saturday the 25th, on the morning of which day we again made Hynish Bay; but the wind, which had been less violent when we started from Tobermory the night before, again commencing to blow strong from the same unpropitious quarter, Return to Hynish, and are driven to Coll. we had only time to land at Hynish, and take on board a salted sheep (which proved a rather unpalatable addition to our provisions), when we were forced to seek shelter in our old quarters at Loch Erin in Coll. As we entered Loch Erin, we saw the Regent (the General Lighthouse Tender) leave the Sound of Mull, and again put back to Tobermory. Next day (the 26th August) we left Loch Erin, and boarded the Regent; but the weather proving boisterous, we were again forced into our old anchorage, while the Regent proceeded with the Engineer, who was then on his annual voyage, to Barrahead Lighthouse, without attempting to go near the Skerryvore. From this date the weather did not prove favourable for a landing until the 30th, when the wind being N.W., we sailed from Loch Erin at daybreak, Return to the Rock. and reached the Skerryvore at ten. We now discharged all the remaining materials which had been shipped for the Rock with a view to complete the pyramid of the barrack, which it was intended should stand the test of a winter, deferring the fixing of the habitable part till next spring.
31st August.—The last day of August was one of considerable discomfort. Our landing at four in the morning was attended with great difficulty and some danger; and throughout the day we were[93] a good deal incommoded by a thick drizzling rain, which continued without intermission. About mid-day the sea rose so much as to render it no longer prudent to delay leaving the Rock, and we therefore embarked. After lying at our moorings until half-past two, in what, to landsmen, was a most distressing sea, Driven to Tyree. we slipped and ran for Hynish Bay, which we reached at 5¹⁄₂ P.M. The weather continued boisterous until next evening (1st September), when the wind went round to the north, and at eight all the men were summoned on board; but although we sailed at daybreak, we could not reach the moorings with daylight; Return to the Rock. and it was not till the morning of the 4th September, about four o’clock, that we could again land on the Rock. We succeeded, in spite of a very unfavourable day, in remaining till three o’clock, Horizontal braces fixed. during which time we fixed the whole of the horizontal braces, and got everything which we had not been able to secure in its place firmly lashed to the ring-bolts on the Rock, after which Driven to Mull. we were forced to leave it for Mull. Heavy gale. The gale continued to blow very hard, without any intermission, for some days; and on the 6th, Timber cast on Tyree. some wreck-timber, covered with goose-barnacles, came ashore among the surf at the beach at Hynish, but no trace of its history was ever found, nor did any rumour reach us of a shipwreck having occurred on this coast. It was not till the 8th that we could again attempt to reach the Skerryvore; when, sailing from Mull with a fair wind, and taking on board at Hynish nine masons, and Mr C. Barclay, foreman of the quarriers, we again landed on it at 2¹⁄₂ P.M. Return to Rock, and farther progress of barrack. We succeeded in getting up the mortar gallery (see Plate V.), and in fixing some of the diagonal braces, and left the Rock about eight. A marrot perched on the vessel’s side this afternoon, much fatigued and evidently desirous to get on board; but the sailors, from some superstitious dread, would not admit the poor bird.
10th September.—We landed at four o’clock, and had a long and good day’s work until daylight left us. We were now within twenty-four hours at most of completing all that could be expected to be done this season; and it was with no small anxiety that I observed[94] a change of wind from N.E. to S.S.W., accompanied by a fall of the sympiesometer; as in the event of a change of weather at that season, it seemed very uncertain when we might again land, and still more uncertain whether our work, in its incomplete state, could resist the winter’s seas.
11th September.—Last day’s work on Rock this season. This was our last day’s work on the Rock this season. We landed at four o’clock with very great difficulty, and some danger of having our boats swamped; and we were forced, owing to the heavy sea which broke upon it, to leave the Rock at high water; but, about one o’clock, we were enabled to return, as the sea fell a little. By dint of great exertions, we got the last of the diagonal braces fixed, and the bats run up with lead and painted, for their protection against corrosion. We also contrived to remove the greater part of the tools from the Rock, but some we were forced to leave to their fate. To the upper part of the pyramid we lashed a water-tight chest, containing biscuits and a cask of water, Precaution for the benefit of shipwrecked seamen.to serve as a means of support to any shipwrecked mariners who might chance to reach the Rock. I also caused some spars to be lashed at various levels, by way of testing the effects of the sea; but to how little purpose, the sequel will shew. Before leaving the Rock, I climbed to the top of the pyramid, View from top of pyramid. from which I now, for the first time, got a bird’s eye view of the various shoals which the stormy state of the sea so well disclosed; and my elevation above the Rock itself decreased the apparent elevation of the rugged ledge so much, that it seemed to me as if each successive wave must sweep right over its surface, and carry us all before it into the wide Atlantic. So loud was the roaring of the wind among the timbers of the barrack, and so hoarse the clamour of the waves, that I could not hear the voices of the men below; and I, with difficulty, occasionally caught the sharp tinkle of the hammers on the Rock. When I looked back upon the works of the season, upon our difficulties, and, I must add, dangers, and the small result of our exertions—for we had only been 165 hours at work on the Rock between the 7th August and the 11th September—I could[95] see that, in good truth, there were many difficulties before us; but there was also much cause for thankfulness, in the many escapes we had made.
After a somewhat precarious embarkation in the boats, and shipping several seas in our way, we reached the vessel, and immediately set sail with three cheers, rejoicing to have thus concluded our season’s work.
After spending a few days at Hynish in making various arrangements for the operations of the next season, which were to embrace the extension of the pier, the completion of the barracks and the erection of sheds and workshops for carrying on the dressing of the materials for the Lighthouse Tower, I left Tyree with the pleasing belief that the successful termination of our first season’s labours might be taken as an omen of future success. But how uncertain are even the most rational sources of satisfaction which Time can furnish! On the 12th November, I received from Mr Hogben, the clerk and store-keeper at Tyree, the unwelcome intelligence Destruction of the barrack during a gale. that the Barrack-house had been destroyed, as was supposed, by the heavy sea of the 3d November; and as his letters contain all the facts of the case in so far as they could be collected at the time, I cannot do better than quote them at full length:—Letter from Mr Hogben. “Skerryvore Lighthouse Works, Tyree, 5th November 1838.—Dear Sir,—I am extremely sorry to inform you, that the barrack erected on Skerryvore Rock has totally disappeared. It was seen on the 31st of October, when I observed no change in its appearance. On the two following days the weather was showery, with haze, so that the Rock was not seen; and on the 3d it rained almost all day, with strong breezes. In the evening the wind increased to a gale, with a great swell, and an extraordinary high tide. Yesterday (Sunday the 4th) the weather was moderate, but the swell prevented the Rock being seen from the low ground. Mr Scott and Charles Barclay, however, having gone to the top of Ben Hynish, got a momentary glimpse of the Rock through the spray, and both were of opinion that the barrack was gone. This was not credited by the[96] workmen who had been employed at it, but this morning we found it to be the case; the Rock was pretty clearly seen, but no trace of the barrack. From the circumstance of the yard of a large vessel, and also a piece of a boom, having come ashore in the direction of the Rock, we think it is not improbable that some wreck has happened, and that some part of it has been thrown upon the barrack by the force of the sea. Should any opportunity occur for going out to the Rock, we shall take advantage of it, in order to give you farther information on the subject. I remain, &c. (Signed) Wm. S. Hogben.” A subsequent letter from Mr Hogben is of the following tenor:—“Skerryvore Lighthouse Works, Tyree, 10th November 1838.—Dear Sir,—This morning, Charles Barclay, with a boat and four men, went out to the Rock to view the site of the barrack; and, the weather being moderate, he got a good landing. The following is the state in which he found everything:—The whole barrack timbers had been carried away, excepting the long beam next the place where the crab stood which drew up the beams, and about seven feet of the long beam opposite the place where the other crab stood. The former of these beams had fallen in the direction of the highest part of the Rock, and had drawn one of the iron stancheons 16 inches. The latter was all in splinters, with one of the iron stancheons broken, and the other bent. The rest of the stancheons were broken at the point between the round and the flat, and some of them were drawn about 9 inches. The iron hoop which bound the top of the beams was lying at the distance of about the length of the beams to the eastward of the centre of the barrack, having one of its screws broken. Five large wooden knees were remaining, a ladder partly broken, some moulds for taking the angle of the beams, and most of the quarry and masons’ tools. The grindstone was thrown from the top of the Rock into a deep hole on the side next Tyree, a distance of about 12 yards, apparently whole. The smith’s forge had disappeared, and the anvil had been thrown about 8 yards to the N.E. of the place, where it was left; it was brought ashore, along[97] with the hoop which encircled the top of the barrack. The iron posts which supported the bellows were standing. The crab on the S.W. side was thrown from its place to the east side of the site of the barrack, a distance of about 15 or 20 yards, and was dashed to pieces, excepting the axle, handles, pinion, and the trunk of the barrel. The other crab was thrown from its place to the N.E., over a part of the rock 5 or 6 feet high, to a distance of about 6 yards, and was found in a similar state to the former. A stone measuring three-fourths of a ton was found near the seat of one of the beams; it had been thrown up from the hole where it had been deposited while cutting the seats for the barrack timbers. One of the ring-bolts near the top of the Rock to which the chain binding the wood had been made fast, was broken close by the surface of the Rock, and the wood was all gone. The mooring buoy has also disappeared. The barrack was seen from the top of Ben Keen-na-vara, by some men on Saturday, 3d November, so that the succeeding night, which was truly awful, must have done the damage. I may mention, that many of the islanders say that they have not seen such a swell as on that evening for about sixteen years. I am happy to say that no damage has been done to the works on shore here, as on that evening the wind was about S.W., and we are pretty much sheltered from the wind in that direction. The shore on the S.W. side of the island is strewed with sea-weed, which has been carried up far beyond the usual reach of the tide. Hoping that the above information will suffice, I remain, &c. (Signed) “Wm. S. Hogben.”
On the day on which I received this discouraging intelligence, I requested a special meeting of the Committee, for the purpose of deliberating as to the best course to be pursued, when I received instructions to proceed to the Rock, and for that purpose to hire a steamer at Glasgow. Proceed to Skerryvore. I accordingly started that very evening for Skerryvore, with the intention at the same time of removing such of the men from Tyree as were not to be employed during the winter. I left Greenock in the steamer Tobermory, accompanied[98] by Mr Macurich of the Lighthouse tender, at midnight of the 14th November, after some delay in repairing a leak in the boiler, which was discovered in time before starting, and reached Hynish at 11 on the forenoon of the 16th, having got a good passage round the Mull of Kintyre. The weather was, however, in every other respect most unfavourable for the purpose; and having merely touched, in passing Tyree, at the workyard at Hynish, to inquire whether any thing farther had transpired, and to take on board Mr Charles Barclay, who had visited the Rock after the loss of the barrack, we at once proceeded and reached Skerryvore about 4 o’clock in the afternoon. The sea ran very high, and there was not the most remote chance of landing, but, having got into the boat, I approached near enough to the Rock to enable me to survey State in which the Rock was found. the melancholy remains of our labours, which seemed to be in the same state in which they were described by Mr Hogben. The beam which lay back on the inclined ledge still kept its place, having been firmly lashed by Mr Charles Barclay to a ring which was near it when he landed on the 10th November; and I could see the remains of some of the stancheons and of the crabs which the sea had left. After waiting, in the hope of a change in the state of the sea, until it was nearly dark, we again turned towards Tyree, in all the gloom of a stormy night, and depressed by mingled disappointment and sad forebodings, occasioned by the fate of our intended asylum from the waves. Owing to the heavy sea, and a strong gale against us, we hung for a long time off Hynish Point, and did not reach the Bay till midnight. Next morning about 7, we came off Hynish, in order to take in the men who were to go home for the winter. The ground was deeply covered with snow, which made the embarkation of so many persons and so much baggage a tedious and uncomfortable operation; and when we sailed, we experienced all the inconveniences of a strong gale and a heavy sea, with the concomitant of a deck covered with passengers, all very sick and much dispirited. Many of the men, indeed, seemed to be as deeply concerned for the loss we had sustained as I myself was. To add to our difficulties,[99] the vessel, under the care of a native pilot, had touched slightly on a rock off Hynish Point, and gave some indications of leaking. We, however, reached Oban in safety.
No. 10.
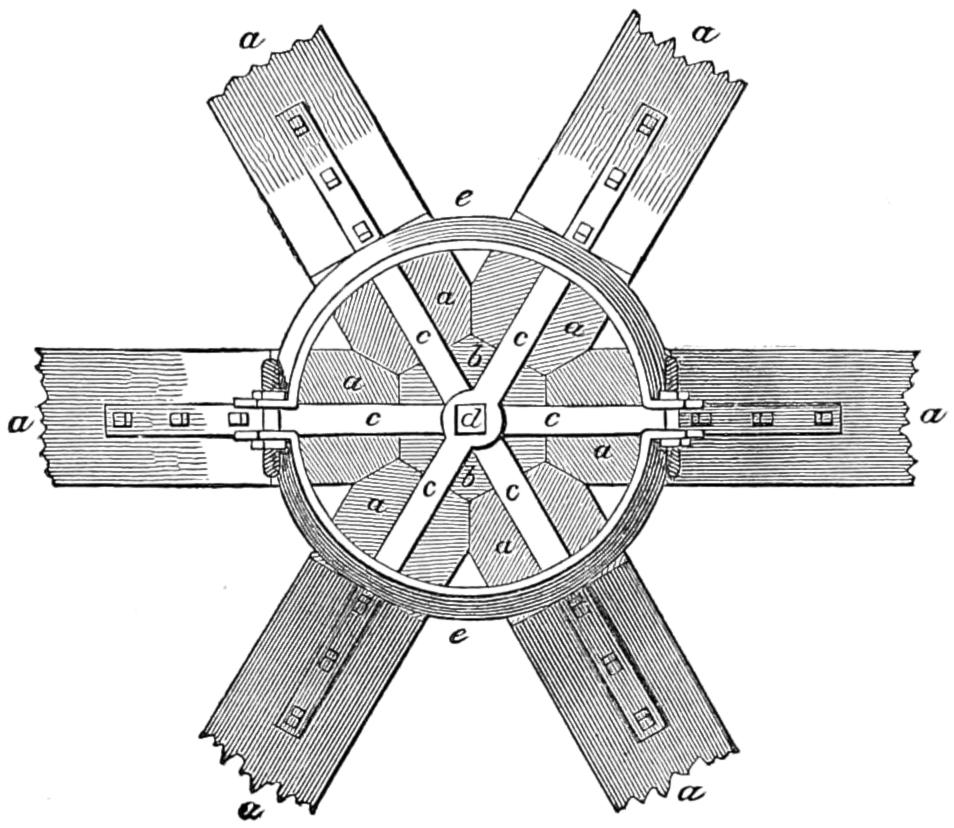
Various conjectures were made as to the cause of the destruction of the barrack. Those who saw it erected were so confident of its stability, that they could not avoid connecting its failure with some injury received from the wreck-timber, which had come ashore on the island of Tyree, two days after the supposed date of the accident. In this opinion they were strengthened by the total destruction of the cranes and other objects on the rock, forgetting that the timber of the barrack itself, when once let loose, must of necessity have proved even a more powerful agent of destruction than the driftwood of the wreck. But whatever doubt may exist as to the Cause of the destruction of the barrack. first cause of the injury, there seems good reason to suppose that the dismemberment of the parts of the structure had commenced with the removal of the horizontal braces, and that the beams, having thus more liberty for play and tremor, had gradually shaken loose the fixtures at the top, which consisted of straps c c, passing right over the tops a a, of the beams and b b, the hexagonal quoin of hardwood already noticed at p. 88, which were secured by means of a central bolt d, and finally girt outside by a ring, e e, as shewn in the annexed woodcut (No. 10.) The moment this dismemberment occurred, the beams would be free to work their own destruction; and the enormous leverage which they exerted, when dashed to and fro by the breakers, would soon snap the iron stancheons at the base, and throw all loose to the waves. The only remaining beam was that which was supported against a ledge of rock, and which had received the sea from the opposite direction[100] to that in which it was found lying. That beam, however, although firmly lashed to the rock by the men who first visited it after the accident, along with Mr Charles Barclay, also disappeared in the course of the winter. As a proof how severely these beams had been dashed by the waves, I may state, that the only remaining part of a beam which I saw attached to the iron stancheons, when I landed in the following spring, was so thoroughly riven and shaken as to be quite like a bundle of lathwood.
No. 11.
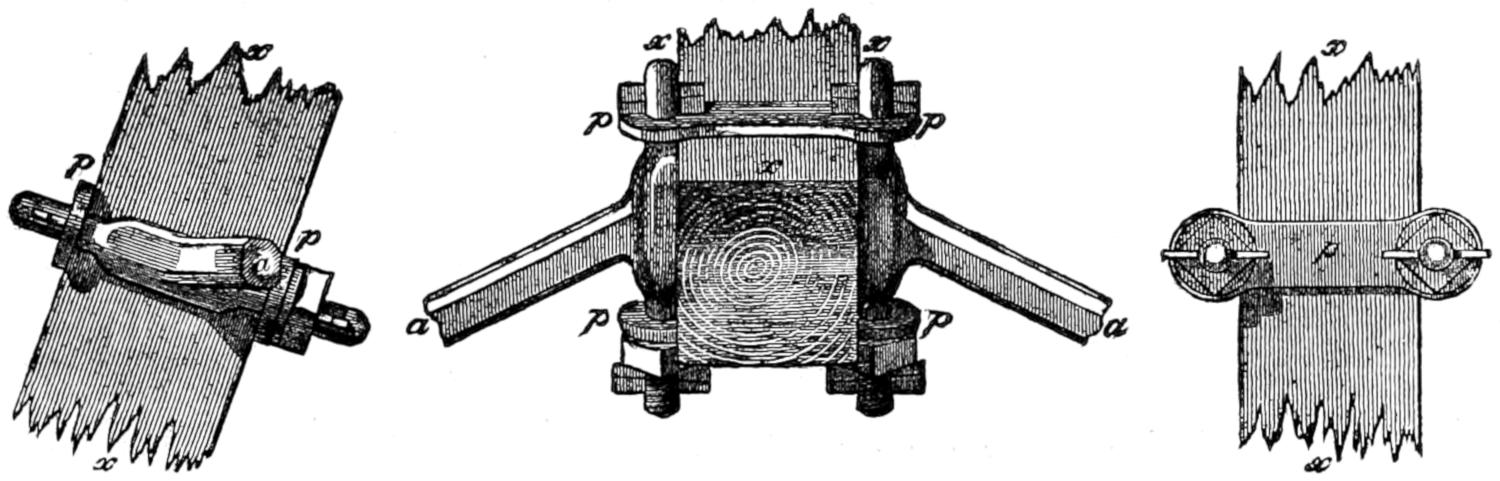
These circumstances by no means shook my belief in the suitableness of the plan adopted for obtaining a temporary dwelling on the rock; but they induced me, as soon as I received authority from the Commissioners, whose confident expectation of final success was not damped by the unhappy issue of our season’s labours, to examine very carefully the whole details of the ties and fastenings.Preparations for a new barrack. In preparing a similar structure for next season, I resolved to strengthen the ties at the top, where I imagined the former failure to have occurred, by adding six strong stancheons a, a (Plate V.), one to each beam, with heads passing through a centre-plate (H), which united them in one as a cap and to which they were secured by strong screws and keys. The nature of those fixtures will be more easily understood by a reference to the figures (1) and (2) in Plate VI., which shew an elevation and plan of the upper part of the beams. In the elevation only the beams A, B, C, are shewn; but in the plan, all the six beams appear mitering at their heads n, n, to the central beam or tie o, o (see also Plate V.), which was introduced to counteract the tendency of the heavy seas that might burst inside the pyramid, and by exerting a powerful force in the vertical direction, might separate the beams at the top. In the Plate (VI.), a, a, are strong stancheons of iron attached to the outside of the beams by bolts, and also by collars r, r, attached to ears g, g. These stancheons being bent into the vertical direction and rounded at the top, passed through the malleable iron plate H, which was held down, and, as already stated, bound the beams together by nuts c, c, and wedges b, b. Through a hole in the centre[101] of this plate, a large spike p was driven, which produced an expansion of the central beam, and thus wedged up or tightened all the joints formed by the mitering of the seven timbers. On each of those stancheons, snugs were formed at e, capable of receiving and retaining in its place against any tendency to move upwards, a strong metallic ring g, which was tightly keyed by wedges at k. Additional ties of iron D, E, F, were also provided, which connected the six beams together in pairs. Each end of those ties was attached to the timbers by three spikes; one tie, D, is shewn a little fore-shortened; another, E, is seen only on the end; while the third F, is shewn as cut off at the middle. Lastly, an important change was made, by the substitution of malleable iron for wooden braces (see Plate V.) b, b, b, b, in the horizontal direction. Fixtures of this kind held the whole more firmly together; and their construction was such that they might firmly embrace each beam, without requiring any means of attachment beyond wedging tightly up; and thus the entire strength of the timbers was unimpaired by the driving of spikes or bolts. Those braces (No. 11), a, a, had, at each end, double knobs, and were pushed up along the beams, until they squeezed the timbers x, x, x between them; plates p, p (having holes in them through which the double knobs of the braces were made to pass), were then put on and keyed and screwed, as shewn in the figure, so[102] that each beam was quite enclosed by fixtures, which were thus independent of spikes or bolts. Thin hardwood wedges were afterwards driven in, wherever they could be inserted between the iron and the timber; and those wedges were “stitched” to the beams with common nails, merely to prevent their dropping downward, after any temporary contraction of the timber from the state of the atmosphere. In all this, I have anticipated what more properly belongs to the works of the season 1839; but I consider it best, for the sake of clearness, to connect this account of the new with the destruction of the old Barrack.
While the operations already described were in progress at the Rock, Works at Hynish. various works were going forward at the workyard in Tyree. About 16 masons, 12 quarriers, and 4 carpenters, were employed in building the barracks for the workmen and in erecting smiths’ and carpenters’ shops. A large room, paved with a stone floor, for drawing out at full size the courses of the Tower and making the moulds for dressing the stones, was also provided; and a platform of squared masonry was set in the workyard, on which the courses were to be laid, before being shipped for the Rock. During the season, the pier had also been carried out 256 feet, to a point 15 feet within the low-water mark. It was also necessary to provide depositories for the security of tools and other implements, as well as a large coal-shed for the supply of the Steamer which was then in the course of being built. It had, as already noticed, been determined that the stores were to be served out at the cost prices of the Greenock market, to be paid for once a month, at the same time that the wages of the men were paid. That arrangement had been carried into effect on a small scale, from the very beginning of the works; but this season it became necessary, owing to the increased number of men, to conduct it on a more extended and systematic plan; and, for that purpose, a person was required to act as storekeeper and clerk. In order also to preserve the provisions[103] from injury by damp and to secure them from the inroads of the needy Celts and from innumerable rats which overrun that part of Tyree, it was found necessary to set apart, as a storehouse, a large room on the second storey of one of the workshops. The chief articles served out in the store were meal, molasses, sugar, coffee, tea, tobacco and butter. The establishment of the store entailed a great deal of trouble, and led to some expense for carriage and packages, as well as to occasional trifling losses in serving out the allowances or from injury sustained in the transport of the goods; but the inhospitable nature of the country, and the remoteness of Tyree from the ordinary steam-boat traffic, made the adoption of some such plan unavoidable. Amongst other inconveniences which attended the store, not the least may be reckoned the frequent importunities, on the part of the native labourers whom we employed, to be permitted to purchase provisions at the workyard; but that was never acceded to, except in cases where dearths (which are of frequent occurrence in the island) rendered the call irresistible. Had their entreaties easily prevailed, we should soon have had the whole population of Tyree as our regular customers at the Store.
Hynish Quarries. The quarries at Hynish, as already stated, were by no means productive. The great proportion of the materials which had been quarried, was found to be applicable only to the building of the pier and the inclosing walls, and to the various erections in the workyard; and not more than one-tenth of the whole could be dressed as blocks for the Tower.
During the numerous occasions on which I had been driven by stress of weather to the neighbouring coasts, I had visited the quarries around Oban and in various parts of Morven and Mull. When so forced to leave what I might more especially call my post, I had an opportunity of seeing the quarries at Ardentallen near Oban, which contain the old red sandstone strongly impregnated with clay. That stone is by no means suitable for the[104] face-work of a marine building, in such a situation as the Skerryvore; while the comparatively small quantity of hearting which could be admitted into such a work, made it inexpedient to seek such materials at so great a distance. In this way, the Ardentallen quarry seemed completely excluded from the field. At another time, in passing through Inverary, I devoted a day to the examination of the quarries which had lately been opened at that place and in which a beautiful porphyry is wrought; but I saw no appearance of very large blocks, or, at all events, nothing that could favour the expectation of a considerable supply. But after carefully weighing the matter, the great masses of granite at the Ross of Mull finally determined my choice in favour of that locality; and the Duke of Argyll having, with the greatest liberality, ratified his predecessor’s grant of liberty to the Lighthouse Board to quarry stones from any part of the Argyll estates, it was resolved to take measures early in the spring of 1839 for opening quarries at North Bay, in Mull, where an excellent station for shipping had been discovered, close to the place where we saw the most promising appearance of rock. This measure seemed the more indispensable, as the last part of the quarry terred[18] or laid bare at Hynish, had greatly disappointed our expectations. The unworkable nature of gneiss rock also and its extreme uncertainty with regard to quality, farther concurred to make a change most desirable. Granite, indeed, is a material in many respects superior to sandstone, gneiss, or porphyry. The first it greatly excels in durability and weight; and, as a stone for the workyard, it is superior to the other two, from its property of being fissile, or easily split in any direction. In this respect it resembles certain parts of some sandstone strata which are commonly called liver[105] rock, of which Craigleith quarry, near Edinburgh, furnishes an excellent example. Porphyry, and, I think, all other igneous rocks (excepting granite), gneiss also, and most of the other primary rocks, have not this property, being fissile only in one plane, so that quarries of those rocks generally turn out very uncouth or irregular stones, which, though they may in some favourable cases possess good natural beds, will always be found to have ragged and irregular joints, which, for the most part, are incapable of being properly dressed.
[18] This term in Scotland denotes the removal of the soil and unsolid material, in order to lay bare the rock previous to working the quarry, and seems obviously to be derived from the Latin “terra,” perhaps through the medium of some old charter. The quantity of terring very much affects the profitable working of a quarry.
During the winter months which intervened between November 1838 and March 1839, a small detachment of men, consisting of three masons, nine quarriers, and one smith, were left at Hynish under the superintendence of Mr Charles Barclay, to clear the landing-place of several patches of rock which encumbered the entrance. Shipping Station and Pier at Hynish. They were also to build some walls of inclosure, and to quarry and dress stones for the pier and other buildings at Hynish. The provision of accommodation for shipping at that place was now naturally regarded as of more urgent necessity than formerly, because the importation of stones from Mull, which the failure of the Tyree stone had rendered unavoidable, led to the necessity of a reshipment of all the materials at Hynish, where they were dressed before being sent to the Rock. It may, perhaps, be naturally enough imagined, that instead of importing the materials to be dressed at Tyree and there reshipped in order to be carried to the Rock, they might have been prepared in Mull, and sent directly to the Skerryvore; but many things concurred to render this inexpedient, if not altogether impracticable. The advantage of being able, by means of a good telescope, in some measure to ascertain the state of the sea at the Rock, the comparative shortness of the passage, which gave the prospect of several cargoes being landed on it in one day during fine weather, and the convenience of communicating with the Rock by signal, were circumstances in themselves quite sufficient to determine my choice in[108] favour of Hynish, as the place from which the materials must be shipped for the Rock, even if there had been no other considerations leading to the same conclusion. But in addition to all this, I could not fail to perceive that Hynish was the only place for the permanent station of the vessel attending on the future Lighthouse; and that on that account alone the construction of a Harbour there was unavoidable. That the arrangement, by which the future station for the Tender was used as the workyard for the operations, was the most judicious that could have been adopted, was fully proved by my subsequent experience of the advantage of assembling all our materials and all our force at a point as near to the Rock as possible, so that we might be at all times ready to supply defects or omissions, and take advantage of every favourable change of the sea or sky.
In the middle of March the Regent conveyed from Aberdeen a detachment of twenty-nine masons and quarriers and five smiths, and the foreman of the workyard, who, together with the men already at Hynish and the native labourers, were to be employed during the season of 1839, in the various departments of the work. On their arrival the men were separated into two small bands, of which the one, consisting of six masons, twelve quarriers, one smith and a foreman, was stationed at North Bay in Mull, where the new quarries were to be opened; while the other had its head quarters at Hynish, and, when not engaged in the work on the Rock itself, was subdivided into smaller parties, varying in number with the nature of the particular operations in which the men were occupied.
On the afternoon of the 19th April I sailed from Greenock in the Regent, for North Bay in Mull, Granite quarries in Mull. where the quarries were to be opened. We had on board the whole materials of the new Barrack, which was to supply the place of that which had been destroyed in the preceding month of November; and we had also a party of carpenters who came to fit up the Barrack in a temporary manner at North Bay, as a residence for the masons who were to[109] be engaged in preparing more permanent dwellings for the quarriers and in forming a landing-wharf for the shipment of the stones for Tyree. It was not till the 25th, after a tedious passage of six days, that we anchored at North Bay; and next morning we had the satisfaction of seeing the steamer, the Skerryvore (by which name she was specially set apart for the service of the works), arrive in the Bay with a party of masons and quarriers, who had been appointed to meet us in order to begin the work.
The necessary arrangements with the Duke of Argyll’s tenants at the Ross of Mull (in which district North Bay is situated) having been already made, no time was lost in erecting the wooden Barrack; and, in seven days after our arrival, the masons and quarriers entered their new habitation under the charge of Mr Charles Stewart, whom I left as foreman of the North Bay works. Mr Stewart and his party, following the example of diligence thus set to them, were not less expeditious in proceeding with the work which had been assigned to them; and by the beginning of August a range of barracks, capable of accommodating forty persons, had been erected, a landing wharf had been built, and various storehouses had been provided, although the quarry had to be opened, and the blocks of stone required for those various works were still in situ at the time of our landing at North Bay three months before.
The landing wharf is placed on a small projecting face of rock in a depth of 12 feet at high water of ordinary spring tides. It presents a face of 40 feet in length, and was provided with wooden fenders for the protection of the vessels loading stones. Landward of it a considerable space was levelled, by cutting and filling, to serve as a yard for storing the quarried materials, so as to be ready for shipment. The quarry itself was opened in the face of a hill, so steep as almost to deserve the name of a cliff; but advantage was taken of a deep gully which intersected it and in it an inclined plane was formed communicating directly with the landing-place. This gully was partly cleared by excavation of the[110] rock and partly, where necessary, its inequalities were smoothed down by filling it with stone shivers; and along its bed thus prepared, longitudinal sleepers of timber were laid, to which edge-rails were attached.
At the top of the incline two iron drums or barrels were set, and round them were wound, in opposite directions, the chains by which the trucks or wagons, loaded with stones from the quarry, were lowered to the wharf below. A powerful break apparatus was attached to those barrels, to check the velocity of the descending wagons, which was also in part counteracted, by making their gravity act as a power to raise the empty wagons in the same manner as is usually practised in coal-mines.
The quarry itself, as already stated, was opened in the face of the cliff, at a point where the successive beds of solid rock seemed to promise the fairest prospect of success. The preliminary operation was to remove a very thin alluvial cover which scarcely concealed from view a large mass of most beautiful granite, whose reddish colour is said to have given the name of Ross[19] to that part of Mull, the shores of which everywhere exhibit massive slopes of that fine rock. The granite is separated very abruptly from the basalts of the surrounding district, so as to leave the Ross purely granitic; but in no part of the whole coast, which abounds with creeks and bays, does the rock appear to be of equal quality, or so conveniently situated for shipping, and so easily accessible to quarriers, as at the spot we had chosen. I know of no instance of a quarry so fully answering the most sanguine expectations as that of the Ross of Mull; and I have never seen a granite quarry of equally great resources, as regards both the quantity and the quality of the material produced. The rock in general yielded easily before well-directed shots, and was separated into large masses, capable of being advantageously cut, with little loss of material, into[111] shapely blocks, by means of wedges, which work remarkably well in that rock. A few weeks after the quarrying operations had been commenced, a single shot detached 150 tons of excellent stone, in the cutting of which into blocks for the Lighthouse Tower little loss of material occurred; and in the course of the season of 1839, although the summer was chiefly spent in the preliminary works above noticed, the Mull quarries produced nearly as much workable material for the Lighthouse Tower as the Hynish quarries had done in three years. In the course of the future working of the quarry, when it came to be more fully opened, its resources were so great, that on one occasion a single shot shook about 570 tons, while another shot detached a mass of 460 tons. In that way, between April 1839 and June 1840, material had been quarried in that single spot, sufficient to supply 4300 selected blocks, varying in weight from ³⁄₄ ton to 2¹⁄₂ tons each. The average monthly produce of the quarries was about 400 tons, and there were generally employed in them 26 quarriers, 3 labourers, and 2 smiths. The quantity of gunpowder consumed in the quarry was small, as it was almost exclusively employed in great bores about 11 feet deep, for the purpose of detaching large masses which had no open side and could not be removed by means of the pinch or crow-bar. When a mass of rock had been thus removed, it was cut up into various portions by means of wedges, and finally subdivided into blocks, hammer (or as it is called quarry) dressed, according to rough moulds, whose dimensions exceeded those of the stones of the various courses of the building by a quantity which was considered sufficient to cover any casualty in the final dressing of the block by the masons at Hynish, and which allowance was generally equal to a film of rock about 1¹⁄₂ inch in depth. The blocks thus roughly formed were shipped for Hynish, distant about 26 miles, through a tempestuous sea, open to the full reach of the Atlantic towards the south-west, sometimes in a small vessel called the “Queen,” belonging to the[112] Commissioners, and sometimes in undecked boats of 16 tons, belonging to the adventurous men of Tyree. The freight usually paid was 5s. a ton, and yet the whole of the blocks for the Lighthouse Tower, and many of those used in the pier at Hynish, were laid down to the number of about 5000, at the rate of 2s. 1¹⁄₂d. per cubic foot, including all the expense of building barracks, opening quarries, freight of stones, and the expense of building and maintaining the small vessel called the “Queen,” above noticed. The stone of the Mull quarries is a reddish or flesh-coloured granite, in which felspar predominates. About 13·66 cubic feet weigh a ton, and it is not quite so hard as the granite of Aberdeen.
[19] Whether from any inflection of the Celtic Rhua, or Roy, or directly from the Italian Rosso, it would, perhaps, be impossible to determine.
As I am not aware that any professional work contains a detailed description of the quarrying of granite, some observations on that subject may not be unacceptable in this place; Observations on the quarrying of granite. and I therefore propose, at the risk of appearing somewhat prolix, to give a pretty minute account of the mode of opening and working a granite quarry, more especially as practised by us at North Bay.
Having laid bare the rock of earth, gravel, or other loose matter (which operation, as I have elsewhere mentioned, is in Scotland technically called terring), and having swept or washed clean the surface of the rock so as to have a good view of the natural seams or joints which traverse it, the next step is to fix the best place for putting in a bore or mine.
In selecting the position of the bore, the direction of the seams and veins of the rock must be duly considered, with a view to employ the force of the explosion to the greatest advantage in separating the natural joints or beds of the rock, instead of shattering the solid masses or posts (as they are called in the language of the quarry) into shivers or fragments.
One thing to be strictly borne in mind is, that the bore should never be in the centre of a fine or large block, but should be placed within a few inches of its back so as not to break the finer rock into small and useless fragments; and care must, at the same time,[113] be taken to keep the bore clear of cracked or unsound rock, as the jumper, in passing through such material, is liable to be jammed by the cracks and fissures before it can be driven to the proposed depth. It is not possible to lay down precise rules for guiding the quarrier in choosing the place of the bore, as his plan must be regulated chiefly by the circumstances of each case; but it may be observed, that having first determined the depth of the hole, it will seldom be found advantageous to keep the bore farther back from the face of the rock than about four-fifths of that depth. The depth itself, also, to which the mine should be carried, is a point for deliberation with the skilful and experienced quarrier, who will take great care not to go so deep as to pass through the solid rock in which he is boring and thus to touch a bed, unless indeed he shall think it advisable to attempt to raise more than one post of rock by a single mine, in which case he will carry the bore through the first post into the second or third as the case may be. But in all cases the boring must be stopt at two inches before coming to the bed or seam of the post in which the mine is to terminate, lest the exploding powder should escape by the bottom of the bore, and thus leave the top of the rock altogether undisturbed. In endeavouring to procure large materials, the bores should in general be as deep as possible. It is only experience, however, which teaches the quarrier to form a sound prognosis as to the direction and level of the beds of the rock at any particular spot, and enables him to choose the most advantageous position and depth for the mines.
In the blasting of granite there are a few general rules which (although it may not be necessary to follow them in every case) may be considered as constituting the best practice. If the bore be a vertical one of the depth of 6 feet, 2¹⁄₂ inches diameter at the top, diminishing to 2 inches at the bottom, may be considered a proportionate caliber. If the bore be a deep one (perhaps of 14 feet), its diameter will require to be 3¹⁄₂ inches at the top, and should diminish to 2³⁄₄ inches at the bottom; and the quantity of powder[114] required for the charge will in most cases be about as much as is required to fill ²⁄₅ths of the hole.[20]
[20] Miners and quarriers, who always work by empirical rules, disregard entirely the line of least resistance as a measure for the charge, and invariably refer to the depth of the bore.
The patent fusee having been inserted among the powder, with its end about the centre of the charge, and the upper part of the bore having been filled up with dried clay, well forced down with a wooden rammer faced with copper, a length of 3 or 4 inches of the fusee should be left outside the bore, to which the match is to be attached. Having cleared away every thing near the blast which can receive any injury and covered up the machinery of the cranes with strong planks, the mine may be said to be ready for being fired; and, on a signal given, by blowing a horn, all hands retreat to a safe distance, with the exception of the fireman, who then lights the match, and follows the others as fast as possible.
If, as already stated, the object in quarrying be to obtain large materials, the bores should, if possible, be deep; and, in that case, the rock will seldom be thrown down in fragments by the blast, but will merely be cracked, and intersected by rents about one inch in width. Recourse must therefore be had to what, in quarry language, is called a Bull, which consists in running a quantity of loose powder into the crack which has been made by the blast, at that part where its explosion seems most likely to throw out the cracked or broken mass in various fragments and disengage them from their place in the rock. In bulling, perhaps twice as much powder as was used in the bore is loosely poured into the crack, care being at the same time taken to get as much of it to go under the bottom of the rock as possible. After enough of powder has been poured into the crack, a quantity of dried smithy ashes, or dry sand, is run in over the powder, so as completely to cover it, except so much as is required to fire it by; and that coating, which is merely superficial, is employed partly to keep down the powder, and partly for security against its being accidentally fired before all things are ready. The fireman having seen every[115] thing cleared away, gives notice to sound the alarm, when all hands escape to a distance in the direction which is supposed to be the safest. The match is then applied, and the fireman retires, as fast and as far as he can, yet so as if possible to keep in view, during his retreat, the progress of the match. The operation of bulling is far more dangerous than the firing of a bore, as the charge is much greater, and not so well confined, so that many splinters are thrown off, and the direction in which they fly varies continually with the direction of the cracks which the original bore may have produced. As might be expected, by far the greater part of the accidents which occur to firemen in granite quarries, arise from that practice.
No. 12
Should it happen, as it sometimes does, that after having gone through those operations, the quarrier fails in getting the cracked mass thrown down to the bottom of the quarry, he varies his mode of attack, and proceeds to bore a row of plug-holes on the face of the rock in such a line as to cut off a part from one end of the shaken mass; and for that purpose he is often obliged to hang a scaffold over the face of the rock on which to stand while boring the holes. Those plug-holes should be slightly inclined, so that, when the wedges, called plugs[21] and feathers, are driven into them, they may rend the rock in such a direction that the piece intended to be cut off may be a little narrower on the inner than the outer face, so that, thus resting on an incline it may be more easily taken out. The plug-holes should be cut at one foot asunder, and bored with a jumper 1¹⁄₂ inch diameter to the depth of 9 inches; and if the plug-holes be deep, and some difficulty in driving be expected, the plugs should be carefully greased or oiled previously to being driven. Having cut off a block as above described, an attempt may be made, if the mass[116] be great, to throw it down by means of bulling; but if it be of lesser dimensions, and there be reason to expect that it may be removed in the ordinary way, the power of the crane may be applied to draw it down. For that purpose, the quarrier employs an instrument called a Dog, which is a strong short hook, armed like a pick on the point with steel, and having a ring in the end of it for the hook of the crane-chain to pass through. Having cut a small hole with a pick, on the upper part of the block which is meant to be removed, the steeled point of the dog is inserted into it, in such a manner that the weight of the crane-chain may retain it steadily in its place. Five or six men then heave on the crane a strain just as much as they suppose it may bear, without danger of carrying away any of its fixtures; and as many men as can find room are, at the same time, employed at the top of the rock, working with crow-bars behind the block, so as to shake it and loosen its hold. The two parties continue their work reciprocally, leading and following,—the men at the crane, still keeping up the strain, and taking care not to heave so much as to break any of the chains, while those on the top continue to shake the block by means of the crow-bars, or throw in stones into the opening, which is always getting wider between the block and the cliff, so as to prevent the loosened mass from falling back into its old place. When the block has been drawn as far forward as to appear just ready to fall over the cliff, one of the most expert men at the crane stands carefully watching the movement of the block; and whenever the stone begins to fall, he instantly throws the crane out of the gear, so as to prevent the wheelwork being pulled to pieces by the tumbling mass getting entangled in the chains, on which it frequently falls and breaks them to pieces. The operation of taking down large blocks from a great height is very tedious, and is often attended with much danger, as the stone, when it falls on the bottom of the quarries, makes the shivers among which it alights fly in all directions with a force which nothing can withstand.
[21] The plug (fig. 12, c c′), and feathers (fig. 12, d d′), are flat pieces of malleable iron, slightly tapered, and forming together a kind of compound wedge, the two feathers being first inserted into the hole, and the plug being driven between them by a series of gentle blows, from malls of the weight of from 30 lb. to 35 lb.
An opening being made in the manner above described, by getting one piece brought down, the same process is continued by[117] cutting off and taking down pieces of eight or ten tons weight, until there be as many blocks in the floor of the quarry as can be easily managed at one time. Those masses are then arranged by means of the crane in convenient positions for being cut up into blocks of the requisite sizes; and as all of them are within range of the crane, they can with its assistance be easily turned over or set in any position. While some of the men are employed in cutting up those blocks, others are clearing away the rubbish, and others are boring holes or making ready for a fresh blast.
No. 13.
If those blocks, which we have supposed to be brought down to the quarry floor and to be ready for cutting, exceed seven feet in depth of cut, their farther subdivision will require the use of the plugs and feathers already described; but if their depth or thickness fall short of that, the ordinary iron wedges will answer. If the cut be of the depth of about 6 feet, the wedges must be placed about 3 inches apart from side to side; but if the depth of cut be less, they may be set 4 or 5 inches asunder. The method of setting in those wedges is as follows:—The person who cuts the wedge-holes generally works in a sitting posture, and if the block will admit of it, he prefers to bestride it, with a stone, as a stool, under each foot. He works with a pick of 16 lb. weight, having a handle only 16 inches long, with which he cuts the first hole generally about 3 inches from the end of the block. The holes are for the most part about 2¹⁄₂ inches deep, and 3¹⁄₂ inches long, and must be well cleared out at the bottom with a sharp pick; and the wedges must be set in a line as fair and straight as possible. Cutting wedges of that kind are of iron, from 7 to 9 inches long, and 2¹⁄₂ inches broad, and weigh about 7 lb. weight each. When in good order they must not be sharp in the mouth, but about ³⁄₈ of an inch thick, to prevent their grounding in the bottom of the hole; for if they but touch the bottom of the hole, they fly out at the first touch of the mall. When the wedges have been all properly arranged for a cut, the workman proceeds to give each of them in succession a gentle tap, so as to make them all fast; and for that purpose he uses a mall[118] about 30 lb. weight (fig. No. 13), and having a handle 2 feet 9 inches long. He then goes over all the wedges, giving each of them a smart blow in regular, yet not too rapid succession, but allowing a little time for the parts of the stone to separate gradually. If the wedges be forced too quickly, there is great danger of the cut being spoiled by its flying out obliquely at one side, and thus not reaching throughout the whole depth of the block. The blocks, when thus subdivided by means of the wedges, are generally nearly of the size required by the rough moulds sent from the workyard, and are fit to be carried to the stone-cutter’s shed.
Fig. 14.
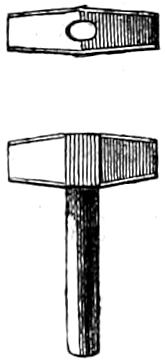
As a conclusion to the above account of quarrying, it may perhaps be thought desirable to give some notion of the probable time required to perform certain parts of that sort of work. In boring holes of 1 inch to 1¹⁄₄ inch in diameter, it may be observed that they are generally done with the hand mall (fig. No. 14), one and the same person striking with the mall with one hand, and turning the boring tool for himself with the other; and in most cases a man will bore 9 or 10 inches an hour in granite rock. If the bore be 1¹⁄₂ inch diameter, as for plugs, three men will generally bore two plug holes in one hour, each hole being about 9 inches deep. If the bore be for blasting and of 2 or 2¹⁄₂ inches diameter, three men will bore, at the rate of one foot per hour, to the depth of 6 or 7 feet; but if the bore be for a large blast of 13 or 14 feet deep, the hole must be 3¹⁄₂ inches in diameter at the top (diminishing to 2³⁄₄ inches at bottom), and will employ three men working hard between two and three days. Bores of that sort, indeed, cannot be made (at least by hand) to a greater depth than 14 or 15 feet, as the weight of a rod of iron, 17 feet in length, and 2 inches in diameter, makes it quite unmanageable for one man either to turn or to lift; while, from its great mass, the strokes of the mall[119] produce little effect on it. The malls used in boring holes, which require three men, are 7 or 8 lb. weight, having handles 3 feet long (fig. No. 15), and are swung over the shoulder, while striking for down bores, in the same manner as a smith’s forehammer is used. An expert cutter with the wedges will make good wages by cutting holes at the rate of 2¹⁄₂d. for a dozen of holes, taking light and heavy cuts as they come to hand.
No. 15.

What has been said above of boring and blasting refers only to downright or vertical bores; but, in the lower parts of a quarry, it is often necessary to have recourse to what are called breast-bores, from their running in a nearly horizontal direction and piercing the front or breast of the rock. Those bores are not so easily made as the downright bores and, in general, are only used where the rock is low, or in taking up bottom rock. They can seldom be carried to a greater depth than about 9 or 10 feet, owing to the difficulty of turning the jumper, and can never be bored quite horizontally, but require as much dip as will retain a little water in the hole to keep the jumper moving. Instead of throwing the mass outward, as is done by down-bores, those breast-bores generally only cut or break the stone in the direction or line of the bore, so that the block always requires to be afterwards removed by bulling, in the manner already described.
Dressing of the Lighthouse blocks. The dressing of the blocks for the Lighthouse Tower, as already mentioned, was one of the most important operations in the workyard at Hynish; and as no writer with whom I am acquainted has given any account of the mode now practised of dressing granite, I hope I shall be excused for attempting, in this place, to give some idea of the method employed by the masons of Aberdeenshire, whose skill in that department of workmanship is well known both in our own and in other countries. As the whole of the materials for the Tower were to be dressed in such a manner as to avoid the necessity of any fitting on the Rock, by[120] the introduction of what are technically called closers, the greatest accuracy in the formation of the moulds from which the stones were to be shaped became necessary. With that view, I had a trainer or radius made with a moveable vernier, capable of sliding along it, so as to give the differences between the readings of the feet, as far as to the thirtieth part of an inch; and I was thus enabled to lay off the batter or slope on each course (according to the quantities in the Table of Co-ordinates in the Appendix) with great nicety, and so to trace very distinctly the contour of the intended column.[22] On the stone floor of an apartment in one of the workshops, the quadrant of each course of the building was carefully drawn out, at full size, and divided into the sectors which were required for preserving a due bond among the joints of the adjoining courses. The form of each stone in the tower having been thus determined by those full-sized draughts, moulds, representing the beds and sides of each stone, were prepared according to them, of seasoned timber, well shielded at the angles with sheet-iron, to prevent their being injured. Those moulds having been marked with reference to the number of the course, and the position of the stones in the wall, were given to the foreman of the workyard, who regulated the work of each of the stone-cutters, often to the number of 70 men. A proper block having been selected for each stone, leaving about 1¹⁄₂ inch all round the extremity of the moulds when applied to its several faces, it was conveyed, by means of the sling-cart, to the shed where it was to be dressed. The shed for dressing granite stones differs in no respect from an ordinary mason’s shed, except in its greater height; but, as the stone cutter, in order to wield his tools to advantage, must, at certain parts of the work, stand on the top of the block, it has been found, that a height of about 15 feet is required for the back-wall of a[121] granite mason’s shed. Each man also requires, for large blocks, a space of about 10 feet (measured along the front of the shed), as his peculiar territory.
[22] Such nicety, I would observe, was by no means superfluous, because the arrangements of the Tower precluded the possibility of using a trainer in building; and as the whole was done by means of plumb-templets, the greatest accuracy in tracing the curve of the Tower became necessary, as the only true basis of good workmanship on the Rock.
When a block has been brought to the shed, the first thing to be done, if it is a large stone of 1¹⁄₂ or 2 tons weight, is to lay it nearly level on the ground, with the side which is to be first dressed uppermost. The form or plan is then sketched upon it according to the mould, and the stone is blocked out with a large hammer weighing 30 or 35 lb. (fig. No. 16), which is the most suitable weight for ordinary men, although a stout man will manage one of 40 lb. well enough, if the block be lying in an advantageous position. When the stone has been thus rudely blocked out, it is set upon its edge with a gentle inclination to one side, so that the mason, who mounts on the top of it, may conveniently use a pick of 18 lb. weight, having a handle three feet long, to dress off very roughly the most prominent parts of its irregular surface. In doing that he makes a great many deep ruts in a downward direction, at the same time taking care that none of them shall be so deep as to fall below the general surface of the stone when finished. When he has in that style dressed as far down the surface of the stone as he can conveniently reach, (and that is generally about half way,) the stone is then thrown over and set up on the opposite edge, when he again mounts upon it, and goes over the rest of the surface in the same manner, until the whole shall be reduced to one rough plane, so that in spite of numerous partial inequalities, the general face may be straight, or what is technically termed out of winding. A stone in that state is also said to be well opened.
No. 16.
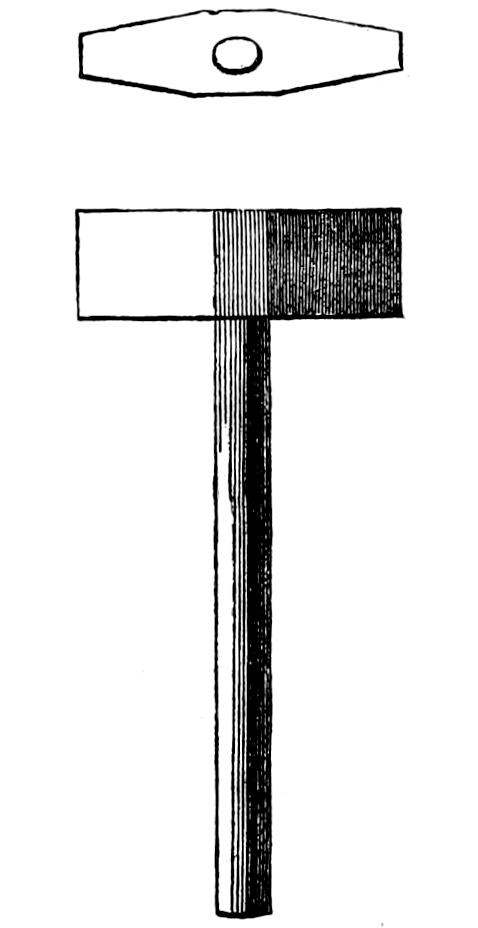
No. 17.
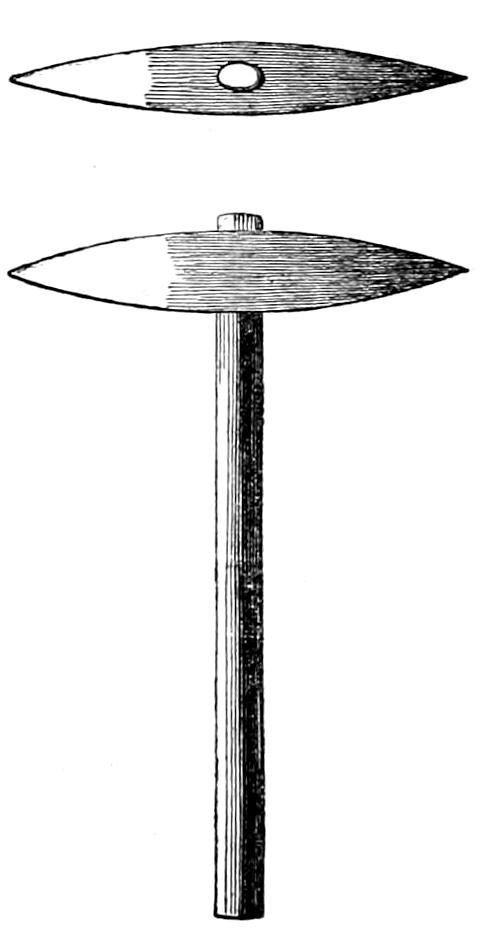
No. 18.

The next step is to raise the stone so that it may incline at about 30° or 40° with the horizon; after which the mason, standing at the higher side, commences to put on the draughts or guide-lines all round the edge of the face which he has just[122] opened. For that purpose he first employs a pick of about 12 lb. weight, having a handle about 2 feet in length (fig. No. 17), with which he dresses a band of about 3 inches broad, taking care that this band or draught be straight and out of winding. He then, with the pick, goes over the whole face between the draughts, dressing off all the ridges which still remain between the ruts which he had made while the stone was standing on edge, as before noticed, so that the whole surface will present the appearance of a pretty regularly dabbed face. Having arrived at that stage, he next proceeds to put on the true draughts (as round the edges of the stone, as in the case of the guide-lines), with the cast-steel chisel or punch (a, a′, fig. No. 18), and a small iron-mall of 3¹⁄₂ lb. weight; and afterwards with the axe, he carefully axes a band about 2¹⁄₂ inches broad, so as to be quite out of winding, and as straight as possible all round. The dressing is then completed between those bands. If the block be a broad one, the mason will probably be able to take in only one half of the face at a time; and, in that case, the stone must be let down at the high side, and the other one raised as high as may be necessary to enable him to work to advantage. If the surface thus dressed, which is in this case supposed to be the largest side, be intended for the bed of a stone, the knobs or high points between the pick-dabs are merely roughly dressed down with a blunt axe, so as to be all as low as the axed lines or draughts round the extremities, and thus to present no convexity on which the stone, when laid, could rock; but if the surface should be meant for a fine face, the dressing must be commenced with a bluntish axe, taking care that all the axe marks be made quite across the stone, at right angles to the side where the workman stands. The whole face having been once gone over in that manner with a blunt axe, a sharper and well ground axe is[123] next used for crossing the first axing in such a manner that all the second axe-marks may be inclined at an angle of 45°, or thereby, with the first. The whole face having been thus brought to a smoother and more uniform surface, the third and last axing follows; and then the mason uses his shortest and lightest axe, which must, for that work, be well ground and sharp. That axing must be done right across the block, or in the same direction as the first axing had been done, and in that state the surface of the stone may be supposed to be fine enough for most kinds of work used in housebuilding or in public works; but for very fine work, such as some sepulchral monuments, or for surfaces which are afterwards to be polished, it is not unusual to axe four or even five times, care being always taken that how often soever that operation may be performed, the axing should never be made twice consecutively in the same direction, for by that precaution alone can a true and even surface be obtained. (The form of the axe is shewn in fig. No. 19.)
No. 19.

No. 20.
The dressing of the first face being finished in the manner described, the block is laid flat on the ground, and the plan or form of the stone is then accurately drawn on it, according to the mould, with some substance that makes a bright or good mark, such as a piece of tile ground sharp, or a thin splinter of logwood. If there be much waste to be taken off beyond the lines so drawn, a hammer, whose weight must be in proportion to the piece to be struck off, is applied; but care must be taken not to come too near the lines with the hammer, and it is generally safe to leave at least an inch outside of them. The piece which is left gives a good hold for the chipper or pincher (fig. No. 20), which is next carefully applied along the line, being steadily held within one hand, and with the other sharply struck with a small iron mall of 3¹⁄₂ lb. weight, having a short handle about 8 inches in length. While the chipper receives sharp strokes in succession with the mall,[124] it must be slowly moved several times along the line from one end of the stone to the other, till the piece projecting beyond the line, or a part of it, breaks off. Such is the power of this small instrument, that it not infrequently cuts down to a depth of 9 or even 12 inches, thereby doing more execution and to greater purpose, than a heavy hammer can generally accomplish, even in the hands of a skilful workman. The chipper is a tool lately introduced; but has now become a most important article in every hewer’s kit. It makes a regular and clean cut, and leaves little to be done by the punches and chisels (fig. No. 18, in p. 122), in preparing the arris of the next face of the stone. The block is now raised a little from the ground, and the workman standing at its higher side, the axing of which he has just finished, puts on with the punches and chisel a fine band or draught along the side next to that just dressed. He then applies to the finished face the square or bevel, according to the inclination of the faces, and dresses a band across the stone at each end of the block; and, finally, joins those two cross bands by means of another band along the back. In that way the external draughts on the second side are completed. He then with the pick and axe dresses away the material between those draughts until the second face is finished; and the same process is repeated for each side of the block which requires to be dressed. If the block be a large one, and it require to be dressed on all its sides, it will, lastly, be cut to the proper thickness or height, which is regulated by means of a gauge, known, in the technical language of the shed, as “a grippers” (fig. No. 21),[23] from its embracing the stone on three sides. It is simply a three-sided iron templet, having one long and one short tail (at right angles to the connecting piece), the space between the two tails shewing the thickness of the stone.
[23] The figure shews “a grippers” for a stone 14 inches thick.
No. 21.
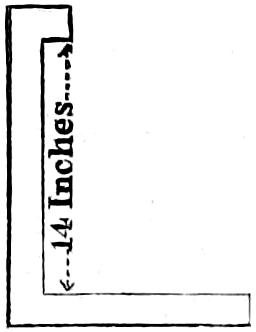
The practical reader will readily see, that what has been said above about the hewing of granite, is chiefly applicable to the dressing[125] of the large stones used in public works, such as docks, bridges, or marine towers; and it may be proper to add, that such heavy materials are always dressed on the ground, and that a piece of wood is placed under each end of the stone as a necessary precaution to prevent its being split by the blows of the mall. In dressing the lighter materials for house building, where a good deal of fine work is generally required, the stones are laid on what is called a banker, similar to that which is used in hewing freestone. The banker is a bench of stone 2¹⁄₂ or 3 feet long, and 2 feet broad, and is raised about 2 feet above the ground, so as to suit the workman’s convenience.
In dressing one of the outside stones of the first or lowest courses of the Skerryvore Tower, a mason was occupied eighty-five hours (see Plans of courses, Plate VIII.); and in dressing one of the largest of the hearting or inner stones of the same courses, fifty-five hours. But as the work proceeded, owing to the greater readiness which the men had acquired in the application of the moulds, gauges and bevels, the time occupied, gradually decreased to the extent of about ten hours for each stone, until the work had been carried on as far as to the thirteenth course, where the number of outside stones was reduced to twenty-four, at which stage of the work, the time required for dressing increased to about one hundred and twenty hours for each outside stone. From that point upwards, the time again gradually decreased till we reached the sixty-fourth course, where it may be stated, that, on an average, a man was employed sixty-three hours in dressing each stone; but the time gained in the last instance seemed to depend less on the readier application of the implements, than on the gradual diminution in the size of the stones, which, from that level upwards, decreased along with the thickness of the wall. But above the sixty-fourth course, a very marked increase in the time of dressing took place, owing to the introduction of the ribband or ring joggles (shewn in the Plans of the 84th and 94th courses, Plate VIII.); and to the substitution of the dovetailed joggles in the place of the square or diamond joggles, which were used in the lower parts of the building. The time[126] required for dressing a stone of the sixty-fifth course was ninety-three hours of one man, a circumstance which strikingly shews, that a small, and, apparently, trifling alteration in the style of workmanship may sometimes increase to a considerable extent, the expense of a great work. Each radiating stone of the eighty-fourth course, which forms the floor that goes quite through the wall, required one hundred and sixty-one hours for its completion; and the other radiating floor-stones, which did not pass quite through the wall to the outside, occupied one man about one hundred and twenty hours. Each centre stone of the floors into which the others were dovetailed, required about three hundred and twenty hours of one man’s time. The time of a labourer occupied in cutting a hole for the dovetailed Lewis bats, by which the stones were raised, was about three hours.
The tools necessary fully to equip a granite mason are as follows:—One dressing hammer about 16 or 18 lb. weight; 6 dressing picks, from 12 to 20 lb. weight; one small hand-mall, or mash-hammer, about 4 lb. weight; 3 stone axes about 7 lb.; 16 or 18 cast-steel punches and chisels, with one or two chippers or pinchers of 2¹⁄₂ lb. weight. One large blocking-hammer of 30 or 32 lb., may very well serve for eight men. The value of a granite mason’s kit may be estimated, when in good working order, at about L.7. A very great revolution has taken place during a few years in the method of working granite. The most important change is the substitution of the hand-mall and chisel in the operation of putting the drafts or bands on the stones, in place of arris-picks, which made the workmanship clumsy, tedious and imperfect, by slowly grinding down the stone at a great expense of labour to the hewer, who was forced to remain bent forward in an irksome posture, without the relief which is obtained by occasionally shifting his position, a change, which, every one who has been long employed in any laborious occupation, knows well how to value. The introduction of the chipper may also be regarded as one of the most important modern improvements in the art of working granite; and[127] had it not been for those changes, the actual expense of dressing the blocks for the Skerryvore Tower, as ascertained from the journals of the works, would have been exceeded by a sum of between L.4000 and L.5000; and it may even be questioned whether it would have been at all practicable with such tools to cut the dovetailed spaces of the floors out of the solid stone.
Excavation of Foundation for the Lighthouse Tower on the Skerryvore Rock. The excavation of the foundation of the Lighthouse Tower was the first operation which engaged my attention at Skerryvore Rock, at the beginning of the season of 1839. It was commenced on the 6th of May, and was continued up to the last hour of our remaining on the Rock, on the 3d of September. A more unpromising prospect of success in any work than that which presented itself at the commencement of our labours, I can scarcely conceive. The great irregularity of the surface, and the extraordinary hardness and unworkable nature of the material, together with the want of room on the Rock, greatly added to the other difficulties and delays, which could not fail, even under the most favourable circumstances, to attend the excavation of a foundation-pit on a rock at the distance of 12 miles from the land. The Rock, as already noticed, is a hard and tough gneiss, and required the expenditure of about four times as much labour and steel for boring as are generally consumed in boring the Aberdeenshire granite.
After a careful survey of the Rock, and having fully weighed all the risks of injuring the foundation, I determined at once to enter upon a horizontal cut, so as to lay bare a level floor of extent sufficient to contain the foundation pit for the Tower. The very rugged and uneven form of the Rock made this an almost necessary precaution, in order to prevent any misconception as to its real state, for it was traversed by numerous veins and bands inclined at various angles, on the position and extent of which the stability of the foundation in no small degree depended. That operation occupied 30 men for 102 days, and required the firing of no fewer than 246 shots, chiefly horizontal, while the quantity of material removed did not greatly exceed 2000 tons. It was a work of some[128] hazard; for the small surface of the Rock confined us within 30, and sometimes within a dozen yards of the mines, while its form afforded us no cover from the flying splinters. The only precautions we could adopt were to cover the mines with mats and with coarse nets, which I had caused to be made during the previous winter, of the old ropes of one of the Lighthouse Tenders, and in each blast to apportion very carefully the charge of powder to the work that was to be done. That was managed with great skill by Charles Barclay, the foreman of the quarriers, who charged all the bores, and, along with myself, fired all the shots. So completely did the simple expedient of covering the bores with nets and mats check the flight of the stones, that, except on one or two occasions, none of the splinters reached us, and all the damage done was a slight injury to one of the cranes. Perhaps, also, our safety may, in some measure, be attributed to a change which I introduced into the mode of charging the horizontal shots, by which all the risk of pushing home the powder in the ordinary mode with the tamping rod is avoided. That change consisted in using a kind of shovel, formed of a rod, armed with a hollow half-cylinder of sheet copper, which contained the powder, and being inverted by giving the rod half a turn round its axis, made the powder drop out when the cylinder reached the bottom of the bore. It was, in all respects, excepting size, the same as the charging-rod used for great guns. The amount of materials removed by blasting, as nearly as I could ascertain, was only about 1000 cubic yards; and, taking all the circumstances into account, it may be doubted whether there be any instance in modern engineering of an operation of so small an extent occupying so much time, and involving so great risk. The blasting of the Rock, however, was not the only difficulty with which we had to contend, for it also became necessary to remove the quarried materials, amounting to about 2000 tons, into the deep water round us, to prevent their being thrown by the waves upon the Rock, and so endangering the future temporary Barrack. That was rather a laborious work, and occupied two cranes, with temporary runs and trucks,[129] during the greater part of the time we spent on the Rock. I am well aware that the quantity of materials which I have just mentioned, will be apt to produce a smile from those who have been chiefly conversant with the gigantic but simple operations which generally characterize the great railways of this country; but if it be remembered that we were at the mercy of the winds and waves of the wide Atlantic, and were every day in the expectation of a sudden call to leave the Rock, and betake ourselves to the vessel, and on several occasions had our cranes and other tools swept into the sea, the slowness of our progress will excite less surprise; and still less will those who duly weigh the dangers of our daily life, both in our little vessel and on the Rock, and who, at the same time, reflect on the many striking proofs which we almost every hour experienced of the care of an Almighty hand, be disposed to withhold their sympathy from the heartfelt expressions of gratitude which often went round our little circle in the boats, as we rowed in the twilight from the Rock to the ship. Isolation from the world, in a situation of common danger, produces amongst most men a freer interchange of the feelings of dependence on the Almighty, than is common in the more chilly intercourse of ordinary life.
With a view to lessen the dangers of blasting in such a situation, I had provided a galvanic battery on the plan proposed by Mr Martyn Roberts, but I used it less frequently than I intended. The attachments of the wires were very liable to be broken from various causes, where there were many men congregated in a small space; and as we could not venture to leave the apparatus on the Rock, the frequent re-shipment of it in a heavy sea was another cause of the derangement of its parts. I soon, therefore, laid it aside, and only had recourse to it when any work was to be done under water, or in cases where the simultaneous firing of several mines (for which it is admirably adapted) was of importance in effecting any special purpose.
[130]
When the floor had been roughly levelled I again carefully surveyed the Rock, with the view of fixing precisely the site of the foundation-pit, and of taking advantage of its form and structure to adopt the largest diameter for the Tower of which the Rock would admit. In some places I found that parts of the Rock, apparently solid, had been undermined by the constant action of the waves, to the distance of 13 feet inward from its face; but none of those cavernous excavations reached the main nucleus, so that, after much deliberation and repeated examinations of all the veins and fissures, I was enabled to mark out a foundation-pit 42 feet in diameter, on one level throughout. That was a point of no small importance; and although it had cost great labour at the very outset, much time was saved by it in the subsequent stages of the work. Not only was the labour thereby avoided of cutting the rock into separate terraces, and fitting the blocks to each successive step, as was done by Smeaton at the Eddystone; but the certainty that we had a level foundation to start from, enabled us at once to commence the dressing of stones without regard to any irregularities in the surface of the Rock; and the building operations, when once commenced, continued unimpeded by the necessity for accommodating the courses to their places in the foundation-pit, so that the Tower soon rose above the level, at which there was the greatest risk of the stones being removed by the waves before the pressure of the superincumbent building had become great enough to retain them in their places.
The outline of the circular foundation pit, 42 feet in diameter, having been traced with a trainer on the rock, numerous jumper-holes were bored in various places, having their bottoms all terminating in one level plane, so as to serve as guides for the depth to which the basin was to be excavated. The depth did not exceed 15 inches below the average level, already laid bare by the cutting of the rough horizontal floor which has just been described; and before the close of the season of 1839, about one-third of the area of[131] the circle had been cleared, and was ready for the final pick-dressing which prepared it for the reception of the first course. The excavation of this circular basin was conducted with the greatest caution, and few shots were permitted to be fired lest the foundation should in any place be shaken by the action of the gunpowder on any of the natural fissures of the Rock. The work was chiefly done by means of what are called plugs and feathers, the form of which has already been shewn in the woodcuts (No. 12, p. 115). In that part of the work the bores were nearly horizontal, and the action of the plug and feathers was to throw up a thin superficial shelf or paring of rock of from 6 to 12 inches in depth, and not more than 2 feet square. By that painful process an area of about 1400 superficial feet was cleared. The chief trouble connected with that operation was cutting, by means of the pick, a vertical face for the entrance of the horizontal jumpers or boring rods; and wherever advantage could be taken of natural fissures it was gladly done. Another considerable source of labour was the dressing of the vertical edges of the basin, as that implied cutting a square check, 15 inches deep and about 130 feet long, in the hardest gneiss rock; and the labour attending which, can only be fully estimated by a practical stone-cutter who has wrought in such a material. The plan employed was to bore all around the periphery of the circle, 1⁵⁄₈ inch vertical jumper-holes, 6 inches apart, to the required depth, and to cut out the stone between them. The surface thus left was afterwards carefully dressed, so as to admit vertical and horizontal moulds, representing truly the form of the masonry which the check was intended to receive. The experience of the labour attending that operation gave me great reason for congratulation on having adopted a foundation on one level throughout, instead of cutting the rock into several terraces, at each of which the same labour of cutting angular checks must necessarily have been encountered. The cutting of the foundation occupied 20 men for 217 days in all, whereof 168 days were in the season of 1839, and the rest in the summer of 1840.
[132]
The minute details given in my account of the destruction of the first Barrack, have entirely superseded the need for any particular description of the fitting up of the second Barrack on the Rock; and I shall therefore confine myself to a brief notice of the work in the chronological order in which it occurred. Fitting up of the Second Barrack on the Rock. On the 1st of July, after the level floor for the foundation of the Tower had been roughly cleared, and all risk of injury from the firing of mines was past, the boring of holes for the fixtures of the second Barrack was begun; and so great were our exertions, that in the short period of fourteen days, the pyramidal frame-work on which the Barrack-house was to stand (see Plate V.), consisting of 13 beams, of about 50 feet in length, with all their braces, ties and stancheons, and the malleable iron cap which secured their union at the top, was firmly fixed on the Rock. After the pyramid was completed, the Barrack-house (which had previously been removed from North Bay, where, as already noticed, it had served as a temporary abode for the men who opened the quarries there), was transported, piece-meal, from Hynish to the Rock as required; for it was not considered prudent, after the experience of last year, to trust, even in the finest part of the season, a great quantity of timber to lashings on the Rock. The fitting-up of the Barrack-house was completed on the 3d September and occupied only eleven days; so that the whole work extended to only twenty-five days, a remarkably short time for such a work, in such a situation. That despatch, indeed, was only obtained by working (as we did both during the excavation of the foundation and the erection of the Barrack), at all times when the weather would permit, from four o’clock in the morning till eight, and even nine in the evening, with an interval of only half-an-hour for breakfast and the same for dinner. The erection of the Barrack was a work of great difficulty and anxiety; for, as every thing depended on the exact union of all its parts, the slightest error in any dimension would have stopped the work until it could be remedied, a delay which, in such a situation, would, at certain stages of its progress,[133] have proved fatal to the whole structure. Sudden death of George Middlemiss. I cannot, therefore, omit this opportunity of paying a tribute, in passing, to the memory of the late Mr George Middlemiss, the foreman of the carpenters who fitted up the Barrack, whose zeal for the completion of the work was very conspicuous. Poor Middlemiss died very suddenly at Hynish, about a fortnight after the completion of his labours on the Rock. He had received some instructions from me, so late as 11 o’clock, on the night of the 20th September; and when one of the men went to call him next morning at 6 o’clock, he was found dead, and in such a state as led Mr Moxey, the surgeon attached to the works, after a careful examination, to conclude, that he had died of paralysis of the heart, about three hours before he was found, or not more than four hours after I had seen him, to all appearance, in perfect health!
Wharf and Landing-place on the Rock. No inconsiderable part of the labour of this season was devoted to the clearing of the landing-place, which was formed in a natural creek (see Plate III.) and in excavating the rocks in front of the line of wharf, so as to admit the vessels carrying the building materials to come alongside of it. That work could only be done at certain times of tide and during very fine weather, and was, therefore, tedious as well as hazardous. After two entire days spent in cutting with a sickle, mounted on a long pole, the thick cover of gigantic sea-weed, which hid the true form of the Rock from view, we were able to mark out the line of the wharf; and after all the mines were bored and charged and the tide had risen, and every one had retired from the spot, the whole were fired at the same instant, by means of the galvanic battery, to the great amazement and even terror of some of the native boatmen, who were obviously much puzzled to trace the mysterious links which connected the drawing of a string at the distance of about 100 yards, with a low murmur, like distant thunder, and a sudden commotion of the waters in the landing-place, which boiled up, and then belched forth a dense cloud of smoke; nor was their surprise lessened,[134] when they saw that it had been followed by a large rent in the rock; for so effectually had the simultaneous firing of the mines done its work, that a flat face for a quay had been cleared in a moment, and little remained to be done, to give the appearance of a regular wharf and to fit it for the approach of a stone lighter, except attaching wooden fenders and a trap ladder.
Ring-bolts, Water-Tanks, and Railways. A good deal of time was also spent in fixing a great many ring-bolts on various parts of the Rock and its outlyers, for the use of the shipping, which we expected to carry stones to the Rock the next season and in clearing a line for a permanent iron railway, about 50 yards long, from the landing wharf to the Tower, the position of which is shewn in Plate III. The railway was used for the conveyance of materials from the stone-lighters to the building, and is now the highway for all the stores which pass from the wharf to the Tower. Means were also taken for laying down two cast-iron water-tanks on the Rock in tolerably sheltered positions, as shewn in Plate III. One of those tanks was completed and filled with water, but the sole-plate only of the other was fixed, as unfortunately one of the plates dropped from the vessel’s side into the water, while the seamen were lowering it into one of the boats, a loss which prevented the second tank from being finished till the next year. Those tanks, together, held about 900 gallons, and contained our chief supply of water during the whole subsequent progress of the works, when there were often about fifty men on the Rock.
Incidents of the Season. I shall conclude this Chapter, by noticing a few incidents which occurred during the season of 1839, serving, in some degree to throw light upon the peculiar difficulties we had to encounter, or tending to shew the importance of the work in which the Commissioners had engaged.
Effects of a gale from the S.W. On the 9th of August a strong gale suddenly sprang up from the S.W., which, while it lasted, caused us much alarm and anxiety at Hynish, whither we had been driven from our station at the Rock to seek shelter at the commencement of the storm. Several[135] small pieces of timber, which we had left on the Rock when we were forced to leave it, came ashore in Balaphuil Bay; and it was generally reported in the Island that the Barrack had, for the second time, been destroyed. That report I did not credit, as I had great confidence in the fixtures which attached it to the Rock; but my anxiety to ascertain the true state of the case, led me to examine the south-eastern shore of Tyree, when all that could be discovered was a few pieces of loose timber, and one of the smith’s cooling tubs, which had been washed from the Rock. Next day, however, the smith’s bellows came ashore in the same Bay, and so little injured, that we had them repaired and put in use again on the Rock. On the 12th of August, when the weather permitted us to return to our station at the Skerryvore, we found all the timbers which had been lashed down with chains to the Rock scattered in every direction around the beams of the Barrack, the smith’s forge overturned, the bellows of course gone; one of the cranes also which had been used for the removal of the excavated materials had been swept away, and not a vestige of it left, except a small piece of one of the wooden stays, which the force of the waves had broken. But that which most of all surprised us, and gave us the greatest concern, as an alarming proof of the force of the sea and a source of great inconvenience and hazard during the rest of the season, was the disappearance of our moorings, which had been lost by the foundering of the cask buoy in the heavy surf which the gale had raised. During all the rest of our stay at the Rock that season, we were forced to ride at anchor in foul rocky ground of the worst and most irregular description, over which the vessel frequently drifted to a considerable distance, occasioning us no small fear for our safety. That was the second set of moorings which had disappeared at Skerryvore; and a stronger proof of the very great power of the western swell can hardly be imagined, as nothing of the kind had happened during the whole time the Bell Rock works were in progress. That circumstance also convinced us of the necessity of[136] adopting vessels of small burden for landing the materials. So great, indeed, was the difficulty of hanging even the boats at the Rock, that on two occasions (on the nights of the 4th May and 12th July) we had both the boats half filled by the sea, and nine or ten men thrown out on the Rock by the kanting of one of the boats at the recoil of the wave. The landing department was indeed, throughout the whole season, attended with great difficulty, and was to me a source of constant anxiety; for, in the daily transport to and from the vessel and the Rock of 30 men, unaccustomed to boating, during a period of four months, it was more than could have been expected that we should have been preserved from the loss of either life or limb. On the night of the 3d September, when we left our anchorage at the Skerryvore for the season, every heart was full of rejoicing, and many cordial expressions of gratitude to our Almighty Protector were uttered in deep whispers by the more seriously disposed men, whose number bore a goodly proportion to our whole band. I cannot omit saying, in this place, that both Mr Macurich, who acted as landing-master on the Rock, and the late Mr Heddle, the master of the steam-tender, conducted the boating department in a most masterly style.
As an aggravation of our difficulties, we were occasionally much annoyed by the unprincipled and cowardly conduct of a few of the seamen, who, despite the contempt of their comrades, fearing or pretending to fear the risk of lying all night so near the face of the Rock, spared no pains to spread alarm, and made several attempts, Mutiny of the Crew. by threatening desertion, to extort a rise of wages. They even spoke of leaving the vessel at the Rock, which they could easily have done by some of the native boats which called in passing to see the progress of the works; and Mr Heddle, the master of the steamer, was forced to dismiss the mutineers on the first occasion when the vessel was driven for shelter to the land, and to rely during the rest of the season on the native boatmen to supply their place. That firm conduct had, for some time afterwards, the desired effect on those who remained; but the spirit of[137] disaffection having spread pretty widely, we had subsequently several other instances of sudden desertion from the service.
In the course of my residence for four months on board the tender moored off the Rock, I had opportunities of witnessing many proofs of the great necessity which existed for a Light on the Skerryvore; and if I had ever entertained any doubt as to the beneficial effects of such an establishment, the experience of the season of 1839 must have entirely removed it. Near approach of Vessels to the Rock, and other circumstances shewing the importance of a Light on the Skerryvore. It often happened that for several days successively, not fewer than five or six vessels of large size, both outward and homeward bound, were visible at distances varying from 3 to 6 miles from the Rock; and much anxiety was often felt by us for the safety of those vessels, several of which approached so near the outlying rocks as to keep us for some time in the most painful suspense. On two occasions, more especially, I was about to direct the steam to be raised, in order that the Skerryvore tender might be sent to warn the masters of vessels of their danger, or if too late for that, to afford them assistance in case of accident. On the 29th of May a large schooner, and on the 13th of June a large brig ran right down upon the western outlyers, called Fresnel’s Rocks (which were covered at the time), and just put about in time to avoid striking; and on the 12th June, a fine foreign barque (apparently a Prussian) passed so close to Bo-Rhua as to leave us for a short time in doubt whether or not she had struck on it. On the 21st of June, also, a large brig came very near the rocks which lie off Tyree, at the base of Ben-Hynish, in trying to avoid Boinshley Rock, which lies about 5 miles to the N.W. of the Skerryvore. Those circumstances, together with the list of shipwrecks already given at page 23, afford strong proofs that the Skerryvore Rock occupies a most fatal position in a great fairway much frequented by large vessels bound to or from ports in the Irish Sea and in the Clyde.
There cannot be a doubt that many vessels have been wrecked on the Skerryvore and its numerous outlyers, being borne down upon the reef by the strong tide which runs at the rate of between[138] four and five miles an hour at the height of spring tides; and the natives of Tyree have many stories about chains and anchors and hidden treasures, with which their fancy has filled every nook of the Rocks. To what extent those stories, which are often most circumstantially told, may be true, it is not easy to determine; but in the end of July 1839, we succeeded, under the guidance of a native boatman, in raising from a creek in one of the detached shelves to the south-west of the main Rock, an anchor worn by the action of the sea to a mere skeleton, a circumstance which so far corroborates the truth of their traditions.
[139]
In describing the progress of the works during the season of 1840, I shall speak of the various departments separately, as in the last chapter, beginning with the workyard at Hynish.
Hynish Workyard. During the preceding winter months, the establishment at Hynish was reduced to about fifty persons, of whom twenty-seven were masons employed chiefly in dressing blocks for the Lighthouse, in laying the stone platform in the workyard (on which each course was adjusted previously to its being shipped for the Rock, to prevent the occurrence of mistakes which might not be easily remedied there), and in building some additional barracks, masons’ sheds and a limekiln for the summer of 1840. The quarriers and labourers formed a party of about eighteen, and were engaged in cutting blocks in the Tyree quarries, which, although unfit for the Lighthouse Tower, were very suitable for the completion of the Pier at Hynish; while nine carpenters had full occupation in making moulds for dressing the Lighthouse blocks, preparing oaken treenails to be used in the lower courses of the Lighthouse Tower, and in dressing handles for the masons’ and quarriers’ tools. In the month of April, a reinforcement of thirty-seven masons from Aberdeen arrived at Hynish; and the greater number of them were at once employed in the dressing of stones for the Tower; while a few assisted in building the dressed materials in a temporary manner on the stone platform in the workyard already mentioned. The number of masons in the workyard, during the summer months, varied considerably,[140] according to the state of the works on the Rock, where seldom fewer than thirty men were stationed throughout the whole working season. But the dressing of the stones for the Tower proceeded with considerable vigour; and notwithstanding the inroads necessarily made upon the men’s time, by their being frequently required to assist in the landing of materials from Mull, a work for which few of the Tyree men were fit, from their awkwardness in the management of cranes and all kinds of machinery or tackling, and also by the constant detachment of a considerable number both of men and of tools for the laborious work of dressing the foundation-pit at the Rock, upwards of 20,000 cubic feet of granite had been dressed and fitted on the platform, when I left Hynish in the end of October 1840.
Hynish Pier. During the whole of the summer, the traffic at the pier at Hynish was so great in landing materials from the Mull quarries, and in shipping stones for the Rock, that much inconvenience was felt from want of room. Nearly 4000 tons were shipped and discharged at the quay, independently altogether of the ballasting of each vessel which discharged at the pier, and the receiving, storing, and finally supplying coals to the steamer, which formed no inconsiderable item of the labour. Every exertion was made to extend the pier, so soon as the works at the Rock were closed for the season and the stone trade with Mull had ceased; and by great perseverance on the part of Mr James Scott, the foreman of the workyard, whom I always found ready, night and day, to second and even to anticipate my wishes in regard to the progress of the works, an additional length of 36 feet was added to the berthage of the quay before the winter had set in.
The Rock. The first landing on the Rock, for the purpose of resuming the work in 1840, was on the 30th April, when all things connected with the Barrack were found in nearly the same state in which we had left them seven months before. The red paint with which we had coated it had become nearly white, partly by a covering of sea-salt, and by blanching of the paint itself, but chiefly towards[141] the top by the soil of the numerous sea-fowl which had perched on the roof. The timbers, also, bore the signs of being wave-washed, and in the more sheltered parts were tufted with the finer kinds of seaweed; the iron-work was much rusted and entirely divested of paint. The door had been firmly secured with lashings and bolts, and some difficulty was experienced in forcing an entrance into the interior, about the state of which, as our future abode, much curiosity was naturally felt by the men, who were desirous to know how it had weathered a seven months’ exposure to the waves of the Atlantic. It was with no small pleasure, therefore, that, when the door was opened and the windows unbarred and the sunshine admitted to dispel its gloom and chilly damp, we found, that although the water had forced its way through some of the imperfect seams in the window-frames, the interior shewed evident signs of the stability of the fabric, and was in some places so dry, that the greater part of the biscuits which we had left the year before, as a store for shipwrecked seamen who might find their way to the Rock, although some of them were wet and pulpy on the side nearest the outer walls, admitted of being dried, and when a little toasted at the fire, were palatable enough to hungry men, so that, in fact, we consumed the greater part of that stock before we entered on our new supply.
The most important change which had occurred during the winter, was the removal of a mass of rock in the neighbourhood of the foundation-pit, which had been shaken by the effects of the blasting operations of the previous year. That mass, the moving of which shewed that a great weight of water had passed over the Rock, weighed about five tons, and had been detached from its bed during a heavy gale from the N.W., in the month of March, and carried right across the foundation-pit to the Barrack, against one of the beams of which it had rested, and had partially injured the iron collars or glands by which the beam was secured. The stone was broken into small fragments by a party of men, who had been appointed to visit the Rock after heavy gales, and had[142] landed on the 27th of March, to see the state of the Barrack. The men, in their anxiety to break down the block, which they feared might injure the Barrack, if thrown against it by the waves, and allured by the smoothness of the sea, most imprudently remained all night, mooring their boat in the landing creek, and trusting to the scanty stock of provisions which they had brought out, with the intention of at once returning to Hynish. The risk involved in such a proceeding, we afterwards had many opportunities of knowing during our stay on the Rock, as we were often forced to make fast all our materials, to prevent their being washed away by the sudden rising of the waves, especially about the time of high-water in spring-tides. The discomforts, however, experienced by the men on that occasion while in the Barrack, without fire, light or bedding, in a cold dark night of spring were such, that several of them did not afterwards much affect the Rock as a residence even in summer.
Owing to the great difficulty of landing on the Rock in the early part of May, few opportunities occurred of preparing the Barrack as a habitation; Life in the Barrack. and it was not until the 14th of that month that we were enabled to take up our quarters in it; and even then we were most uncomfortably lodged, as many of the smaller fittings which are essential to a wind-and-water-tight habitation had not been completed. During the first month we suffered much from the flooding of our apartments with water, at times when heavy sprays lashed the walls of the Barrack with great violence and also during rainy weather; and in northerly gales we had much difficulty in keeping ourselves warm. On one occasion, also, we were fourteen days without communication with the shore or the steamer; and during the greater part of that time we saw nothing but white fields of foam as far as the eye could reach, and heard nothing but the whistling of the wind and the thunder of the waves, which were at times so loud as to make it almost impossible to hear any one speak. For several days, the seas rose so high as to prevent our attempting to go down to[143] the Rock; and the cold and comfortless nature of our abode reduced all hands to the necessity of seeking warmth in bed, where (rising only to our meals) we generally spent the greater part of the day listening to the howling of the winds and the beating of the waves, which occasionally made the house tremble in a startling manner. Such a scene, with the ruins of the former barrack not 20 yards from us, was calculated only to inspire the most desponding anticipations; and I well remember the undefined sense of dread that flashed across my mind, on being awakened one night by a heavy sea which struck the Barrack, and made my cot or hammock swing inwards from the wall, and was immediately followed by a cry of terror from the men in the apartment above me, most of whom, startled by the sound and tremour, immediately sprang from their berths to the floor, impressed with the idea that the whole fabric had been washed into the sea. The alarm, however, was very short and the solemn pause, which succeeded the cry, was soon followed by words of reassurance and congratulation. Towards the end of the fourteen days I began to grow very uneasy, as our provisions were drawing to a close; and when we were at length justified, by the state of the sea on the rock, in making the signal to those on shore (at the hour fixed for pointing the telescope at Hynish on the Barrack), that a landing could be effected, we had not more than twenty-four hours’ provision on the Rock, so that when the steamer came in sight she was hailed by all hands with the greatest joy!
The construction of the Barrack has already been very fully described, and a glance at Plate V. will be sufficient to give a pretty correct idea of the nature of our singular dwelling. Immediately under the wooden tower was an open gallery, the floor of which was removed at the end of each season, so as to allow free space for the passage of the sea during the storms of winter, but on which, during the summer, we kept the stock of coals, the tool-chests, the beef and beer casks, and other smaller materials which we could not, even at that season, safely leave on the Rock itself.[144] Next came the kitchen and provision store, a six-sided apartment about 12 feet in diameter and somewhat more than 7 feet high, in which small space, curtailed as it was by the seven beams which passed through it, stood a caboose, capable of cooking for forty men, and various cupboards and lockers, lined with tin, for holding the biscuits, meal, flour, barley and other things needful for the sustenance of the human frame. That apartment, for protection against fire, was coated, partly with tin and partly with sheet-lead, which latter, although not in all respects the most desirable material to come in contact with that element, was found to be the only one which we could in some parts conveniently apply. The next storey was divided into two apartments, whereof one was shared by Mr Thomas Macurich, who superintended the landing of all the materials and Mr Charles Stewart, the foreman of the builders, and the other was allotted to myself. The apartments thus occupied consisted of a twelve-sided narrow space twisted around a centre pyramid, whose bevelled faces formed, as will in part be seen by inspecting Plate V., their sloping walls on one side. The half of that space constituted my apartment, which, I think, would be generally pronounced not over commodious; and when it is added that it contained my bed, desk, chair and table, and a stock of groceries, it will readily be imagined I had little room to spare for myself. So much attention was paid to economy of space, that the recesses of the pyramid formed by the meeting of the beams were boarded over and made into cupboards; while my cot, or framed hammock (which, during the night, rested upon brackets which could be folded close to the wall when not required), was, during the day, hoisted by pullies to the roof of the apartment, so as to leave me as much space to move about in as a prisoner could expect. The cornice of the apartment consisted of a narrow shelf adorned with books, which I found very needful helps to solitary life. The highest apartment was also twelve-sided, surmounted by a pyramidal roof and a small six-sided lantern or ventilator, and was lined round the sides with four tiers of berths, capable of accommodating thirty[145] people. The closeness of that room was most intolerable, especially during the heat of fine weather in summer, at which time several of the men preferred taking a nap on the rock, with the clear blue sky for a canopy. The economy of our life on the Rock was strange enough. At half-past three in the morning we were called, and at four the work commenced, continuing till eight, when half-an-hour was given for breakfast: after which it was carried on till two, when another half-hour was given for dinner; and the work was again resumed and continued till seven, eight, and even nine o’clock, when anything urgent was in hand. Supper was then produced and eaten with more leisure and comfort in the cool of the evening. Such protracted exertion produced a continual drowsiness, and almost every one who sat down fell fast asleep. I have myself repeatedly fallen asleep in the middle of breakfast or dinner; and have not unfrequently awakened, pen in hand, with a half-written word on the paper! Yet life on the Skerryvore Rock was by no means destitute of its peculiar pleasures. The grandeur of the ocean’s rage, the deep murmur of the waves, the hoarse cry of the sea-birds, which wheeled continually over us, especially at our meals, the low moaning of the wind, or the gorgeous brightness of a glassy sea and a cloudless sky, and the solemn stillness of a deep blue vault, studded with stars, or cheered by the splendours of the full moon, were the phases of external things that often arrested our thoughts in a situation where, with all the bustle that sometimes prevailed, there was necessarily so much time for reflection. Those changes, together with the continual succession of hopes and fears connected with the important work in which we were engaged, and the oft-recurring calls for advice or direction, as well as occasional hours devoted to reading and correspondence, and the pleasures of news from home, were more than sufficient to reconcile me to, nay, to make me really enjoy, an uninterrupted residence, on one occasion, of not less than five weeks on that desert Rock.
During the first half of the season 30 men were engaged 14 hours[146] a day in the preparation of Foundation-pit. the foundation-pit, which, as already said, was a work of the greatest labour. The Rock, indeed, was in many places so hard as often to make it seem hopeless that tools could make any impression on it. The time employed in the excavation and the number of tools expended on it, were very great, as a pick seldom stood more than three strokes in the harder quartzose veins; but our perseverance was at length amply rewarded by obtaining a foundation so level and so fairly wrought throughout the whole area of a circle 42 feet in diameter, as to present to the view the appearance of a gigantic basin of variegated marble; and so much pleased were the workmen themselves with the result of their protracted toil, that many of them expressed serious regret that the foundation must soon be covered up so, as (we trusted), never to be seen again. In the dressing of the Rock much inconvenience arose from the small splinters which flew out before the tools, sometimes rising to the height of 40 feet, and coming in at the windows of the Barrack; and after several injuries had been sustained, I at length found it necessary to send to Glasgow for fencing masks to protect the men’s faces. In all our work, nothing was more grudged than the occasional loss of half a day in baling out the water from the foundation-pit after it had been filled by a heavy sea.
Landing of materials on the Rock. Before we had made an actual trial of landing stones on a Rock at the distance of 12 miles from the nearest shore, exposed to the incessant beating of Atlantic waves, there was much room for doubt as to the measure of success to be expected; and, as the time approached, I naturally looked to the attempt with increasing anxiety, as to an experiment in a great measure decisive of the future complexion of our operations. Four small vessels, carrying from 16 to 19 tons, had been built at Leith and Dumbarton, for the purpose of carrying the stones on their decks, so as to admit of their being easily lifted by the crane, and so to avoid the risk which would have been incurred by any attempt to raise stones by a crane from the hold of a vessel moored to a rock[147] in the open sea and moving about with every wave. Had that been attempted, the crane would, on many occasions, have been pulled down before the stone could be cleared from the hold. The vessels were very similar to those which were used for the same purpose at the Bell Rock; and I therefore beg leave to refer the reader to page 509, and to Plate XI. of my Father’s account of that work, for a description of them. Being decked all over, to give room for cargo (for they carried nothing in the hold but empty casks for the purpose of floating them in the event of their sustaining any injury), they were towed between Hynish and the Rock by the steamer, and being cast off as near the landing-place as possible, were taken by the boats to the creek, and moored with warps to the fenders at the quay.
The first trial of the lighters in landing stones on the Rock was made on the 20th of June, on which occasion both the steamer and the stone craft were decorated with flags; and due honour was done to the occasion of landing the first stone, by firing a salvo shot and drinking success to the works. The landing service throughout the whole progress of the works was one of much difficulty and anxiety and many narrow escapes were made; but it was managed with great prudence, and at the same time with unremitting energy, by Messrs Macurich and Heddle, in their several departments, both ashore and afloat. On many occasions the men who steered the lighters ran great risks; and it was often found necessary to lash them to the rails, to prevent their being thrown overboard by the sudden bounds of the vessels, or being carried away by the weight of water which swept their decks as they were towed through a heavy sea. Sometimes, also, we were forced, owing to the rush of the sea into the creek, which threatened to lift the vessels on the top of the Rock, to draw out the loaded lighters from the wharf without landing a single stone, after they had been towed through a stormy passage of 13 miles; and one day, during the very best part of the season, so sudden was the bounding of the vessel before the sea, that eight large warps were snapped[148] like threads as the lighter was carried violently before a crested wave which rolled unexpectedly into the creek, while those who stood on her deck were thrown flat on their faces and imagined that the vessel had been laid high and dry on the top of the Rock. During the whole season, however, in the course of landing 800 tons of masonry on the Rock, too often in that dangerous manner, none of the dressed stones received any great damage, nor was any other injury of importance sustained.
The building of the Tower was commenced on the 4th July; Building the first stone. but it was not till the 7th that the ceremony of laying the foundation-stone was performed by His Grace the Duke of Argyll, who, as proprietor of the adjacent Island of Tyree, took a great interest in the success of the works, and on that day visited the Skerryvore with the Duchess of Argyll, the Marquis of Lorne, Lady Emma Campbell, and a party of friends, in the Toward Castle steamer. On that occasion His Grace expressed himself much pleased with the works and kindly left with me a donation of L.10 for the workmen.
The building operations in 1840 were entirely carried on by means of two cranes with moveable jibs, of which one was fixed just beyond the foundation, at the place shewn in Plate III., between the landing quay and the Tower, and was chiefly used in bringing forward the materials; and the other, placed in the centre of the Tower, served for laying the stones, and was raised along with the rise of the building. So perfectly had the stones been dressed in the workyard at Tyree, that no alteration or paring of the beds or joints was required; and such was the facility afforded by the building apparatus, that by working 14 hours, we occasionally set, through the activity of Mr Charles Stewart, the foreman builder, so many as 85 blocks in a day. The first course of masonry was laid by means of a wooden trainer; but the place of all the subsequent stones was, as already noticed, regulated by the use of plumb-templets, whose inner faces were arcs of the generating hyperbola. By those means we succeeded in setting, in a[149] most perfect manner, six courses, which carried the building to the height of 8 feet 2 inches, and contained a mass equal to 10,780 cubic feet. That quantity is not greatly less than the whole materials of the Eddystone Lighthouse Tower, which, according to my computations from the drawings of Smeaton, do not exceed 13,300 cubic feet, and is somewhat more than one-third of the contents of the Bell Rock Tower, which are about 28,500 cubic feet. That frustum was also nearly equal to one-fifth part of the whole mass of the proposed building, which is about 56,000 cubic feet. Of the six courses, the first three are of Hynish gneiss, and the rest are of granite from the Ross of Mull. The comparative merits of those two materials may be stated as follows:—The Hynish stone is harder, and susceptible of finer workmanship, and perhaps its most perfect blocks are more durable; but it requires much more labour in dressing than the Mull granite, which is more homogeneous in its structure and is not intersected by hard veins, like those which occur in the gneiss of Tyree. There is good reason also for concluding that the Mull stone is sufficiently durable, because it contains but a small proportion of micaceous matter, and in its texture closely resembles some of the blocks of St Oran’s chapel in the neighbouring Island of Iona, which have resisted the action of the weather, it is believed, for more than 600 years and still retain the marks left by the tools of the workmen. I had also carefully compared the density of the Hynish and Mull stones, by weighing blocks of known dimensions, and found that it requires 13·16 cubic feet of the former, and 13·66 cubic feet of the latter to weigh one ton, a difference much less than the appearance of the stone would lead one to expect. A Tower of the dimensions of that at Skerryvore, built entirely of Hynish stone, would have weighed about 4308 tons, while the same mass of Mull stone would weigh 4252 tons, leaving a difference of not more than 156 tons in favour of the Hynish stone.
The mortar employed in the building was composed of equal parts of Aberdda lime and Pozzolano earth, and was therefore[150] identical, in its composition, with that used by Smeaton at the Eddystone. Not having been able, after searching the neighbouring islands, to obtain good sand, I found it inexpedient to adopt the proportion of equal parts of lime, sand, and Pozzolano, which were so successfully used at the Bell Rock; but so perfect was the adhesion of the mortar used at the Skerryvore, that in that mass of 800 tons only two small leaks were discernible, which being ripped or opened with an iron, and allowed to run dry, were afterwards carefully repointed, and have never since shewn the slightest symptoms of leaking.
[151]
Hynish workyard. The workyard at Hynish presented a very busy scene during the summer and winter of 1840; and the desolation and misery of the surrounding hamlets of Tyree seemed to enhance the satisfaction of looking on our small colony, where about 150 souls were collected in a neat quadrangle of cleanly houses, conspicuous by their chimnies and windows amongst the hovels of the poor Hebrideans, who generally make no outlet for the smoke in their gloomy dwellings, but permit it to escape by the doors. The regular meals and comfortable lodgings and the cleanly and energetic habits of the Lowland workmen, whose days were spent in toil and their evenings, most generally, in the sober recreations of reading and singing, formed a cheering contrast to the listless, dispirited, and squalid look of the poor Celts, who have none of the comforts of civilized life and are equally ignorant of the value of time and the pleasures of activity.
The number of masons employed in 1841, varied from 60 to 84 and they were chiefly engaged in dressing blocks for the Lighthouse-Tower, in discharging the cargoes of vessels loaded with stone from Mull and also in shipping stones for the Rock, in which operation, their acquaintance with the handling of dressed materials and their readiness in working the cranes, made them very useful in directing and also in working along with the native labourers, who, partly from incapacity and partly from excessive indolence, could not be trusted for a moment to themselves. During[152] that year, upwards of 38,000 cubic feet of granite were dressed into blocks with straight beds and joints, and with faces of double curvature, so as to suit the contour of the Tower, when arranged in the wall. The blocks were also fitted with stone joggles, for retaining them in their places, and with lewis-holes for raising them in the manner usually practised in building materials of that description. Of those materials upwards of 70 blocks were floor-stones (see Plans of 84th and 85th courses, Plate VIII.), dovetailed on the heads, checked on the joints and having a plain surface on the upper and a concave one on the under bed. The necessity of preserving throughout their entire joints a perfect uniformity of bearing, made the dressing of those materials a work of great nicety; and each stone, as before noticed, being cut according to moulds, was fitted temporarily in its place on the platform at Hynish, previously to its being laid aside as ready for transport to the Rock. Those various operations were conducted with great care; and the stones, which were regularly arranged and numbered according to a schedule, formed, at the time I left the workyard in the end of October, a considerable pile, bearing ample testimony to the diligence and zeal of Mr James Scott, the foreman of the workyard and leader of the party ashore.
Owing to the uncertain and stormy weather in spring, it was not till the 13th of May, that the first landing was effected on the Rock. The Rock. The result of our visit, however, was most satisfactory. We found the Barrack quite as we had last seen it six months before; and not one joint of the pile of masonry, which we had left exposed to the waves, had been shaken or started. The Railway and Landing Wharf, although much exposed to the breach of the sea, had survived the winter’s storms with no greater damage than the loss of one of the sleepers or beams, on which the rails rested, which had been torn by the waves from its fixtures to the rock. It was not till a week after our first landing that we were enabled again to take up our quarters on the Rock; for we had few landings in the mean time, and some of them, owing to the heavy surf[153] which played round the Rock, were of no very satisfactory kind. Our first experience of this season was indeed far from inviting. So difficult was the first landing, that we were forced to direct all our endeavours to laying in a small stock of provisions in the Barrack, before being left on the Rock; and, considering the scanty nature of the supplies which the weather permitted us to secure, it was thought prudent to restrict the number of men to eight masons and myself, with as many tools as we could land, to enable them to make the necessary repairs and arrangements before fairly commencing for the season the works of a more strictly progressive character. The vessel then returned to Tyree with the rest of the men and all the heavy apparatus which we could not land; and, to add to the unpleasantness of being left in such a position, with the improbability of a visit from the vessel for several days, one of the masons took alarmingly ill soon after the steamer was too far off for a signal, and suffered so acutely during the whole night, that his piercing cries in the spasms which accompanied his disorder, combined with the howling of a strong north-wester and the incessant lash of the waves, deprived the whole party of sleep during the first night. In this uncomfortable predicament, until the steamer returned on the 22d, we spent two days exposed to winds piercingly cold and in apartments soaked with spray, which found its way through inlets which had been made by the winter’s storms. We were not sorry, at the same time, to have an opportunity of removing the poor man to the care of Dr Campbell, the surgeon who was attached to the workyard at Hynish and of reinforcing our stock of provisions and the detachment of men. We also succeeded in landing the cranes and other building apparatus, which, owing to the heavy surf on the 20th, we had not been able to accomplish.
The few first days after getting fairly established in our habitation for the season, were occupied in extending the railway to a point on the northern part of the Rock, somewhat sheltered during certain seas (see Plate III.), where a crane for stowing the materials[154] previously to building them had been erected; and thus it was not till the 25th of May that the first cargo of stones was landed. Next day a crane (then thirty-four years old), which had been used in the building of the Bell Rock Lighthouse, was placed on the top of the masonry, and the more cheering operations of mixing the mortar and of setting stones were begun.
In spite of the unfavourable state of the weather and the continual distraction of our exertions, occasioned by storms and the landing of materials, we continued our operations with such vigour as to complete the solid part of the masonry of the Tower on the 8th July. Until the building had reached to the level of 15 feet, the work was carried on by the use of two jib-cranes, one on the Rock and the other on the Tower, by means of which latter the stones were set, after being brought to hand by the first. But above that level, shear-legs similar to those used at the Eddystone, were employed. Those shear-legs were about 50 feet high, and were erected in the situation, at the side of the Tower, shewn in Plate III. They consisted of two spars attached at the base to jointed sockets batted into the Rock, and connected at the top by means of a crosshead of timber. The jointed sockets permitted the shears to hang forward at any angle suited to the level and distance of the part of the Tower to be reached; and chain guys both in front and behind, secured them from falling either backwards or forwards. At the crosshead hung an iron sheave with a chain, one end of which was provided with a hook for raising stones, while the other was wound around the barrel of a crab machine well batted down to the rock, by working which the blocks were raised to such a level as to be within reach of the building crane on the top of the masonry. The shear-poles were used, until the building of the Tower was completed, to raise the stones the first lift of forty feet above the Rock. In the later stages of the work, the stones, instead of being taken by the building cranes directly from the shear-poles, were raised from storey to storey by means of crabs placed inside the Tower, which worked chains, reeved through[155] sheaves hanging from the end of beams projecting from the windows. Such beams are called needles, and are described at page 504, and shewn in Plate IX., fig. 3, of my Father’s Account of the Bell Rock Lighthouse, where they were used for the same purpose.
During the early part of the season the weather was intensely cold, with showers of sleet and heavier showers of spray, which dashed round us in all directions, to the great discomfort of the poor masons, whose apartments did not admit of a large wardrobe, while they had not the benefit of much room for drying their clothes at the small coboose or cooking-stove in the Barrack. For days together, also, the men were left without building materials, owing to the impossibility of landing them, or, what was worse, without the power of building what we had on hand in consequence of the violence of the winds. During such times we often felt much anxiety about the safety of the stones which we had piled on the rock ready for being built; and it took no small trouble, by the occasional application of the crane, to save them from being swept into the sea by the surf. The Waves. Nothing struck me more than the illusive effect produced on the mind by the great waves which rolled past the rock. The rapidity of their movements, and the noise which accompanied their passage through the gullies and rents of the rugged reef, seemed to give them the appearance of being much larger than they really were; and, even when viewed from the Tower, after it had risen to the height of 30 feet, they seemed, on approaching the rock, to be on the eve of washing right over the top of the building and sweeping all before them into the sea. It was a long time before, by continually watching the waves and comparing their apparent height with the results of their impact on the rock, we were enabled to correct our notions of their magnitude, so as to mark the approach of their crested curling heads with composure; and some of the party never became sufficiently familiarized with those visitors, to avoid suddenly looking round[156] when the rush of a breaker was heard behind them, or recoiling a few paces when they saw its towering crest apparently about to burst in a torrent over their heads. It was only after a long residence on the rock and continual experimental observation, that I acquired confidence to approach within a few feet of the point which I expected the breakers to reach. I occasionally suffered for my temerity, by being thoroughly drenched with spray; but by long perseverance, I attained considerable skill in predicting the limits of their influence, though ever and anon an extraordinary wave overthrew all our confidence, by bursting far above the boundaries which we had assigned in our minds. That, however, did not generally occur in calm weather, but after strong gales from the N.W., when the waves had assumed the larger and more flattened form known by the name of the ground-swell. To gauge the height of those waves by means of a vertical rod, graduated with large divisions, so as to be read at a little distance, as the waves washed it in passing, was an object I had long in view; but I found it utterly impossible to apply any fixture in the deep water, in a situation fitted for the purpose. By making numerous comparisons, however, of the waves, with various known points of rock near the main Rock, and by availing myself of the observations of some of the more intelligent of the masons, I was led to conclude, that the greatest elevation of an unbroken wave, measuring from the hollow to the crest, does not, in the sea around the Skerryvore, exceed 15 feet; but the sailors, perhaps from their being less accustomed to accurate measurement, generally estimated it at 30 or even 40 feet. Colours of breaking Waves. I was often much interested, while I sat watching the waves that boiled round us on every side, to observe the peculiar tints which they assumed at the moment of breaking, passing as they did from the bluish-green colour of solid water by very rapid changes, to a delicate and very evanescent blush of rose colour, which invariably accompanied their greatest state of comminution or disintegration. Those appearances I have[157] often observed in other places, and I supposed them to be produced by reflection from the thin plates of water; and took them for indications of the perfect homogeneousness of the sea-water, in regard to density, and also of the similarity of its condition at the moment of breaking.
The Seals. Amongst the many wonders of the “great deep,” which we witnessed at the Skerryvore, not the least is the agility and power displayed by the unshapely seal. I have often seen half a dozen of those animals round the Rock, playing on the surface or riding on the crests of curling waves, come so close as to permit us to see their eyes and head, and lead us to expect that they would be thrown high and dry at the foot of the Tower; when suddenly they performed a somersault within a few feet of the Rock, and diving into the flaky and wreathing foam, disappeared and as suddenly reappeared a hundred yards off, uttering a strange low cry, as we supposed, of satisfaction at having caught a fish. At such times the surf often drove among the crevices of the Rock a bleeding cod, from whose back a seal had taken a single moderate bite, leaving the rest to some less fastidious fisher.
The latter part of the season, although not so stormy as the first, was far from being favourable for the building operations which, on one occasion, even during the month of July, were suspended for five days by a violent gale, which made it unsafe to attempt standing on the Tower. Happily the wind was from the N.E., a quarter from which it has comparatively little power in raising heavy seas, otherwise we should infallibly have lost a large part of the dressed materials which lay piled on the Rock, and, in all probability, should have had our work thus prematurely cut short in the middle of summer.
After building a few courses above the level of the solid part of the Tower, the jib-crane could no longer be conveniently used, and recourse was had to a balance-crane, which, during the previous winter, I had caused to be constructed at Edinburgh, in the workshop of Mr James Dove. That apparatus, which, except as[158] to its greater size and strength, in order to suit the greater dimensions of the Tower, was almost identical with that which was used at the Bell Rock, is shewn in Plate IX.; and it is only necessary, in this place, to notice its general construction and mode of working, which is also shewn in Plate XVII. of my Father’s Account of the Bell Rock Lighthouse. In the hollow of the Tower, a cast-iron pipe or pillar was erected, susceptible of being lengthened as the Tower rose, by means of additional pieces of pillar let in by spigot and faucet joints; and on the pillar a frame of iron was placed capable of revolving freely round it, and carrying two trussed arms and a double train of barrels and gearing. On the one arm hung a cylindric weight of cast-iron, which could be moved along it by means of the gearing, so as to increase or diminish by leverage its effect as a counterpoise; and on the other was a roller. The roller was so connected with the weight on the opposite arm, as to move along with it, receding from, or approaching to, the centre pillar of iron in the same manner as the weight did. From the roller hung a sheave, over which a chain moved, with a hook at the end for raising the stones. When a stone was to be raised, the weight and the sheave were drawn out to the end of the arms of the crane, which projected over the outside of the walls of the Tower, and they were held in their places by simply locking the gearing which moved them. The second train of gearing was then brought into play to work the chain which hung over the sheave, and so to raise the stone to a height sufficient to clear the top of the wall. When in that position, the first train of gearing was slowly unlocked and the slight declivity inwards from the end of the arms formed an inclined plane, along which the roller carrying the sheave was allowed slowly to move (one man using a break on the gearing to prevent a rapid run), while the first train of gearing was slowly wound by the others, so as to take up the chain which passed over the sheave, and thus to keep the stone from descending too low in proportion as it approached the centre of the Tower. When the stone so[159] raised had reached such a position as to hang right over the wall, the crane was made to turn round the centre column in any direction that was necessary, in order to bring it exactly above the place where it was to be set; and by working either train of gearing, it could be moved horizontally or vertically in any way that was required. The men who wrought the crane, stood on two small stages of planks attached to either side of the framework, and moving round the shaft along with it.
The balance-crane was safely landed on the Rock on the 20th July and on the 25th it was erected in working order on the top of the masonry. On the afternoon of that day, I had the satisfaction of seeing it put to a severe trial in raising a stone of nearly two tons weight and drawing it from the shear-poles already noticed to the top of the building. As that trial was made at an earlier stage of the works than was originally intended, the Tower was of larger diameter than was quite suited to the arrangements of the crane, which was consequently subjected to the weight of the stone at the very point of the jib. I felt no small anxiety as to the result, and had taken the precaution to relieve the centre pillar or shaft, on which the crane swung, from part of its burden, by means of a guy attached to a lewis-bat on the top of the building; yet even with that aid, the point of the jib was depressed 6 or 8 inches on a length of 14 feet. That test, however, having been successfully passed and not the slightest trace of any injury having been discoverable in any part of the crane, we continued to work it with perfect confidence and in the most satisfactory manner throughout the whole season until the close of the Rock operations for the year on the 17th of August.
The mass of masonry built during the season was 30,300 cubic feet, a quantity considerably more than double that contained in the Eddystone and somewhat more than the mass of the Bell Rock. The whole was very carefully set and when gauged at the upper bed of each course was found to preserve the diameter due to the[160] height, according to the calculated dimensions, within a fraction rarely exceeding ¹⁄₁₆th of an inch. The height of the mass also, when measured, exceeded the specified height only by half an inch. The mortar employed was composed of equal parts of lime from the Halkin Mountain in North Wales and Pozzolano; and I consider it if possible superior to that produced from the lime of Aberdda. When we left the Rock this season, two apartments were covered in and the third was nearly completed, as will appear from the section (Plate III.) (on which the progress of the several seasons is marked), and only about one-third of the whole Tower remained to be built.
Our last work on the Rock before leaving it for the season on the 17th August, was to cover the balance-crane with a strong tarpaulin in order to protect it as much as possible from the weather and also to make a temporary lightning-conductor from the top of the building to the sea.
The extent of work done during the season of 1841 at the Rock, must in a great measure be attributed to the advantage of steam attendance, without which numerous favourable opportunities of landing materials must necessarily have been lost, from the uncertainty which pervades all the movements of sailing craft. The number of lighters towed out and discharged at the Rock was 120; and it is remarkable that no accident of importance occurred, although many risks were run, from the breaking of warps while the craft lay moored to the landing quay during heavy seas. I cannot omit in this place to record my sense of the services rendered to the works by the late Mr James Heddle, who commanded the steamer and who died from some consumptive disease soon after the close of the season’s operations. Mr Heddle’s health had been somewhat enfeebled towards the latter part of the autumn; and his excessive exertions and continued exposure during his arduous service, in some measure, I fear, hastened the crisis of his disease, which at length terminated suddenly by the rupture of an abscess[161] in the lungs. Of his anxiety to forward the work, and his unwearied exertion in the discharge of his harassing duty at Skerryvore, which frequently allowed him less than twenty hours sleep in a week, I cannot speak too highly, as I consider his intrepidity and zeal to have been one of the most efficient causes of our success ever since the commencement of the works on the Rock in 1839. Mr Heddle possessed attainments superior to those generally found among persons in his walk of life and was in every respect a most estimable man.
On the 17th of April 1842, I made my first landing on the Skerryvore, for the season, State of the Rock in Spring of 1842. and found traces of very heavy seas having passed over the Rock during the preceding winter. Its surface was washed quite clean from all the scattered materials which were left lying on it at the end of the last season; and the building, to the height of 6 or 8 feet from the foundation, was covered with a thick coating of green sea-weed. The railway had suffered considerably from large stones having been thrown upon it; and several blocks of about half a ton in weight were found wedged into the deep fissures of the Rock, and lying among the main timbers of the Barrack. Heavy sprays had been playing over the Tower, in the upper uncovered apartment of which a great number of water-worn pebbles or boulders were found. Those stones had been raised by the heavy surf and deposited on the floor of the apartment and on the top of the wall at a height of no less than 60 feet above high watermark; but the balance-crane, which had stood all winter on the top of the Tower, had sustained no damage, although the canvass cover was torn to shreds by the action of the weather. In the Barrack every thing was in good order except the smoke-funnel, which, from the effects of the sea-water, was riddled full of holes and required to be completely renewed.
As I had resolved to keep, during the summer of 1842, a complement of about eighteen or twenty seamen on the Rock, in addition to the usual detachment of masons, in order to work the crabs[164] for raising the materials to the top of the Tower by successive stages; Commencement of Rock operations. my first step was to set about preparing additional accommodation in the Barrack, by converting the open gallery (called store for coals, &c., in Plate V.), immediately below the cook-house, into a covered apartment for lodgings for the additional hands. I accordingly landed on the 20th of April, with a stock of provisions, water and fuel and a party of joiners and a smith, to prepare that apartment by simply flooring over the joists of the gallery and closing the triangular, or rather trapezoïdal, spaces between the uprights of the Barrack, with double planking, protected on the seams with painted canvass, so as to render them impervious to the heavy sprays which, even in summer, dashed forcibly on the lower parts of the Barrack. Windows were formed on the sides least exposed to the intrusion of the sea; but, with all our precautions, we could not succeed in keeping dry even the cots or hammocks, which were suspended there; and it must be admitted that the addition to the Barrack proved, in bad weather, but a comfortless retreat, the inconveniences of which few but seamen would have patiently endured. Those discomforts, however, were to a certain extent, counterbalanced by some advantages which that singular abode possessed in hot weather; for, at such times, its inhabitants enjoyed more room, freer air, and more tolerable temperature, than any of their neighbours in the highest storey could obtain, owing to the greater number of persons in that part of the Barrack and its exposure to the heat of the cook’s stove.
During the remainder of the month of April and the commencement of May we had frequent stiff gales; and it often happened that the men could not venture out of the Barrack, owing to the heavy sea which swept over the Rock. The crane, too, which had been erected at the wharf for unloading the stones, although its top stood about 8 feet above the Rock, was often buried in the breakers and seemed in hourly danger of being carried away, an event which we were the more ready to fear from our experience[165] in a former season, when the crane disappeared during a heavy westerly gale. The sea on those occasions also broke so heavily on the Barrack, that the windows of my apartment, which were about 55 feet above the sea, were often darkened by the sheet of water which flowed over them after the house had been struck by a wave. From those causes it was not till the 18th May that we were enabled to occupy the Rock in full force; and on the day following we commenced building the 38th course on the top of the last year’s work.
After that period we had a long continuance of north-easterly winds, which always brought both smooth water for landing materials and dry weather for building; so that by the 23d of May our work had made such progress and the Tower had risen so high, that the chain of the balance-crane, which had been raised along with the building, by sliding it upwards on the cast-iron pillar or shaft placed in the centre of the Tower, could not reach the top of the shear-poles, by which the stones were raised to the level of about 40 feet above the Rock; and it was found necessary to rig from the lowest window a beam or needle (in the manner described at page 155, and as also shewn in Plate IX. of my Father’s Account of the Bell-Rock Lighthouse), as an intermediate stage between the top of the Tower and the shear-poles on the Rock. The needle, as already noticed, projected horizontally from the window and the stones were raised by a chain which passed over the sheave at its outer end and was wrought by means of a crab placed in the interior of the Tower. In that manner we continued for about six weeks, with little interruption from the weather, to raise the blocks of stone to the top of the Tower by successive needles from storey to storey; while the mortar, lewis-bats and other lighter materials were raised at once by means of a line wrought by a windlass placed on the Rock.
On the night of Saturday the 9th of July, however, a heavy sea, caused by a combination of high tides and strong gales, threw down some of the stones of the belt course which lay piled up[166] round the base of the Tower ready to be raised for building; and they were with great difficulty, but most happily, saved from the insatiable deep. The loss of any of the stones of that course would have been a serious obstacle to the progress of the works and might have prevented our completing the erection of the lantern until next year; and indeed, as that course formed a prominent feature of the Tower, any slight injury even to the arris or corners of the outer face would have been much to be regretted. It was with great satisfaction, therefore, that it was found on examination next morning that none of the stones had sustained the slightest damage.
Last Stone. On the 21st July the last stones of the Tower were safely landed on the Rock, under a salute from the steamer, as an expression, no doubt, of the satisfaction which the commander Mr Kerr and his crew naturally felt at having successfully brought out not fewer than 75 lighter loads, or about 1500 tons, of stone during the season, as well as in some measure of their joy at the prospect of a speedy and happy termination of our arduous labours. The process of landing, indeed, owing to the fine weather that prevailed throughout the season, was very easy, compared with that of former years; in proof of which, I may state, that in 1841, there were often as many as five warps broken at a single landing, while in 1842, not a single rope was broken in the discharging of the stones. On the 25th July the last stone of the parapet or top-course was built; and immediately thereafter we proceeded to remove from the Tower, the balance-crane and the cast-iron pillar on which it was swung, and to make way for the erection of the Lantern.
In looking back upon the works we found great cause for thankfulness for the successful conclusion of the building operations, without loss of life, or even the occurrence of any serious accident, excepting the destruction of the first Barrack in November 1839. It also gave me great satisfaction to reflect that, however difficult a rigid adherence to scrupulous accuracy of workmanship may be in such a situation as the Skerryvore, it had nevertheless,[167] from the exactness with which the stones were dressed, on no occasion been necessary, throughout the execution of the whole work, to deviate from the rule which I had laid down of carefully gauging the diameter of each course and of admitting no variation from the true form materially exceeding ¹⁄₈ inch. Every part of the stone work, indeed, was fitted in an accurate manner and the floor stones, in particular, which serve as ties across the building, were finely dressed and carefully set. All opportunities were also embraced, whenever it was practicable, to grout each course over night that the recent masonry might be in a state fit for building upon in the morning; and by those precautions and the peculiar properties of the mortar used, any disadvantages from very rapid building were entirely avoided. Even the elliptic cavetto which forms the cornice and which projects no less than three feet from the face of the wall, although bearing a very heavy entablature or plinth, never gave any signs of settling outwards; and when I examined it from a stage hung from the end of the balance-crane just before it was removed, there was no appearance of any change in the thickness of the joints, although the outer heads of the stones had been purposely kept a little high to allow for any tendency to settlement. The effect of the cornice is very bold and striking and is quite in accordance with the simple and almost severe style of the pillar itself. The masonry of the Tower is 137 feet 11 inches in height and it contains 58,580 cubic feet or about 4308 tons.
The day after landing the last stone of the parapet, the steamer started from Tyree for Greenock, with two lighters in tow, for the transport of The Lantern. the Lantern; and by the 10th of August the whole was landed on the Rock. No time was lost in preparing the beds for the sole-plates of the Lantern, and that operation had been nearly completed when my Father, in the course of his annual tour of inspection, as Engineer for the Northern Lights, visited the Rock, two days after the iron work had been landed. By the 16th the whole of the sashes and the frame of the roof were to[168] their places; and on the same day the fixtures of the lightning-conductor were completed. On the 18th of August Mr Bruce, the Sheriff of Argyll, and some gentlemen who accompanied him and had spent the preceding night at Hynish, visited the Rock; and, after breakfasting at the base of the Tower, ascended to the top and minutely inspected every part of the work. They afterwards returned to Hynish, whither I accompanied them and had an opportunity of pointing out to Mr Bruce the various works in progress there. The party sailed for Oban in the afternoon of the same day.
From want of room on the Rock it was found necessary to build the roof of the Lantern in separate pieces instead of rivetting together the sheets of which it was composed on the ground, and raising the whole to the top in one mass, as is usually done; but, in spite of that disadvantage, the work was brought to a close for the season on the 14th September, on which day the glazing of the Lantern was completed and the glass was covered with a framework of timber to protect it from the sea-fowls which frequent in myriads the Rock and the Tower. The workmen were, on the same day, removed from the Rock, although with much difficulty, owing to the heavy surf which broke over the landing-place and rendered the embarkation more perilous than almost any I had before experienced at the Skerryvore.
[169]
The shores of Tyree, as already often noticed in these pages, and as deplored by Martin 140 years ago, in his Account of the Hebrides, afford few places of safety fit even for boats. It had therefore been determined, by the Commissioners, that any attempt at Harbour Works. the construction of a harbour should be strictly confined to the provision of a place of shelter for the vessel which was to attend the Lighthouse. Much attention had been bestowed on the subject, not merely by myself during my five years’ acquaintance with Tyree, but also by Mr Thomas Stevenson, who succeeded me in the charge of the works at Hynish, at the time when I was appointed Engineer to the Lighthouse Board in January 1843, after the completion of the masonry of the Tower. A small sandy beach at Hynish, which lies embayed between rugged rocks, had been selected as the fittest place for the pier; and all the materials had been landed and shipped there, so that we naturally looked to it as the site for the projected harbour, not only as presenting works already finished, which might be made available as part of a more extended plan, but as a place which, during an experience of some years, had justified our anticipations as to its being less frequently disturbed during stormy weather than most of the neighbouring creeks. All that was contemplated in the proposed plan, was to form a small basin in which the vessel could lie sheltered in all states of the weather, and from which she could find an easy departure in any condition of the sea which[170] would permit a landing to be made on the Rock. The Skerryvore Steamer having been sold and a small vessel of 35 tons, named the “Francis,” having been purchased at Deal, the dock accommodation at Hynish was, for the sake of economy, laid out with reference to the shelter of that vessel. It was calculated that a basin 100 feet in length and 50 feet wide, would afford sufficient room for such a vessel; and as her draught of water is between 7 and 8 feet, it was thought sufficient to provide for a depth of about 12 feet at high water of spring-tides, which, it was expected, would render the dock accessible during good springs at about three quarters flood.
The exposure of the shore at Hynish, to the effects of heavy westerly swells, made it desirable to avoid carrying the entrance of the basin so far seaward, as, under more favourable circumstances, would undoubtedly have been done; and it was accordingly determined that the landing pier should be extended to about 40 feet seaward of low-water mark, and terminated in a round head, as shewn in Plate X., having a talus wall on its seaward face, composed of rough blocks, arranged in courses regularly receding, so as to form a slope of 45° of inclination, as shewn in Plate XI. The inner face of that pier, being nearly vertical and guarded by fenders of timber, had served as the quay for landing and shipping stones and other stores and it now forms one side of the basin or dock. The other side consists of a shorter talus wall, built about 60 feet to the westward of the first, and, together with the crossheads projecting from each wall and containing the gateway, completes the inclosure of the basin. In the gateway, booms are employed, as the shifting nature of the sand and the heavy seas render gates inadmissible. The space contained between those walls was left completely dry at low water of spring-tides, and was chiefly composed of rock, covered with a thin layer of shifting sand, which varied in depth with the state of the wind and sea. The rocky matter, consisting of decomposed gneiss, was excavated to the extent of about 5000 tons, in three separate[171] compartments, protected by successive dams of rubble masonry, built with Pozzolano mortar, and presenting an aggregate area of 7339 square feet. Those dams, two feet thick, proved so water-tight, that by the aid of a small hand-pump, the excavation and the building of the entrance heads of the booms went regularly forward without any delay, although the men worked in the bottom of the pit, surrounded on all sides by the sea, which, at high water of spring-tides, rose 17 feet above them. The dams were sheltered from the action of the swell by a temporary breakwater of heavy blocks, which formed a convenient roadway for the transport of the materials during the progress of the works, and which were removed at the close of the operations.
The talus wall for protecting the seaward side of the harbour, has about 60 feet of its foundation laid in a depth of water varying at low spring-tides from 18 inches to 3¹⁄₂ feet. The mode of its construction, as already stated, is shewn in Plate XI. It is surmounted by a strong parapet of rustic masonry of Mull granite, and is altogether a most substantial piece of work.
The idea of a tide-basin with boom-gates facing the breach of Atlantic waves is somewhat novel and was not very hastily entertained by me at first; but the most complete success has attended the plan. During my occasional visits to the works in the course of the summer 1843, our attention had been often occupied with considering the probability of the sand shutting up the basin; and as a single tide during heavy winds from the N.W., made great changes on the appearance of the beach, we feared that the vessel might often be imprisoned within the boomgates by a bank of sand heaped against them by the sea. To such an extent did the accumulation go before the harbour was fully opened, that on many occasions there was not water for a rowboat to pass between the boom-heads even at the highest spring-tides. The only remedy for such an evil, was obviously to attempt some mode of artificial scouring; and for that purpose, it was proposed to divert several small streams which run from Ben Hynish and the neighbouring[172] hills through the grounds at Hynish, into one feeder, and pen them up in a pond, so as to afford the means of scouring the entrance to the basin from the incumbrance of the loose sand which might choke it. Those streams were repeatedly gauged during the summer and were found to deliver from 13 to 50 cubic feet of water per minute, according to the state of the weather,—a supply which seemed ample for the purpose in view. The sand at Hynish is of a light nature and is easily acted on by currents of very feeble power. It consists of comminuted shells and requires about 25¹⁄₂ cubic feet to make a ton, instead of 24 feet, which is the common allowance for silicious sand. The leave of the Duke of Argyll and also of the Farmer at Hynish, having been obtained, various cuts were made and the stream was diverted into a pond capable of containing about 175,000 cubic feet and provided with a waste-weir and with sluices for opening the communication between the pond and the scouring tunnel, from which the water flows in a stream of about 9 square feet of area, at the rate of about 260 feet per minute for a period of 1¹⁄₄ hour. The operation of scouring is performed at low water and is generally found quite sufficient for the purpose of clearing a passage down to the bare rock in a single tide. Nothing can be more satisfactory than to witness the effect of that process in opening the entrance to a basin apparently inaccessible; and but for such an arrangement, the dock must have remained permanently choked with sand and sea-weed. The position of the various works is marked in Plate X., which shews the ground at Hynish.
On the side of the dock stands a crane, which is used for various purposes connected with the shipment and discharging of materials. It also serves for raising the booms, by means of a double hook, which can be attached to the chain and which embraces the pegs in the centre of each boom, shewn in Plate XI. The two tiers of booms are firmly lashed down by means of chains passing through ring-bolts in the manner shewn in the section (Plate XI.), so as to prevent their rising with the tide.
[173]
The necessity of providing somewhere in the neighbouring island of Tyree for the proper accommodation of the vessel which was to wait upon the Lighthouse (if it could ever have been a matter of doubt), was abundantly demonstrated by the experience of 1843, and more especially by that of the months of November and December. Owing to the shortness of the day and the distance of any place of shelter from the Skerryvore, together with the difficulty of landing on the Rock and the extreme variableness and uncertainty of the climate, the Regent Tender, although constantly waiting on the coast and making trials on every occasion that seemed to offer any prospect of success, could not effect any communication with the people who had been left on the Rock, during a period of no less than seven long weeks. The poor seamen who were living in the Barrack passed that time most drearily, for not only had their clothes been literally worn to rags, but they suffered the want of many things dearer to them than clothes, and amongst others of tobacco, the failure of the supply of which they had despondingly recorded in chalk on the walls of their prison-house, with the date of the occurrence! Unless, therefore, the vessel had been stationed near the rock, the few casual and uncertain opportunities which occur at intervals, during the short days of winter, would often have been lost, and the future maintenance of the Light rendered excessively precarious. The experience of subsequent years, during which the relief of the Light-keepers has been kept up with considerable regularity, shews that the small Harbour at Hynish forms a most important integral part of the Establishment of Skerryvore, than which I believe no Lighthouse on the coast is more comfortable as a residence.
In connection with the Harbour at Hynish, I naturally notice the erection of a Bo Pheg Beacon. Beacon on a rock called Bo Pheg, which is dry only at low water of spring tides. It lies about one mile NE. from Hynish Point, (See Plates II. and X.) right in the track of the Tender in its passage to and from the Lighthouse. From the great difficulty of landing on that small rock,[174] over which the sea almost continually breaks, even in very fine weather, the shortness of the time during which the men could remain at work, and the want of room on its irregular surface of about 16 yards square, the erection of a beacon proved to be a work of great difficulty. The Beacon consisted of an open frame-work of iron, (somewhat on the same plan as that which is described in the Appendix) and calculated to offer little opposition to the free passage of the waves; but before all the fixtures could be completed, the heavy storms of the winter of 1844, acting on its unfinished base (the bats of which were only partially secured), destroyed it piecemeal, at a season when no landing could be effected, nor any effort made to save almost any part of it from the sea. In the ensuing summer, a second Beacon, consisting of a hollow cone, composed of iron plates, united together by strong flanges and attached to the rock by webbed flanges round its base with strong bats passing through them, was fixed down to the rock; and in order to increase its weight, the interior was filled with concrete gravel. That structure also has since yielded to the force of the waves, after giving slight indications of movement, an effect which I attribute chiefly to the smallness of the base, which the narrow limits of the rock unhappily prescribe.
Another necessary part of the Establishment at Hynish, was the provision of Lightkeepers’ and Seamen’s House. dwelling-houses for the families of the Lightkeepers and Seamen and of Storehouses of various kinds. Those were partly built on purpose and partly consisted of altered forms of the buildings which had been found necessary as barracks for workmen and stores for materials, during the progress of the works.
On landing on the Rock, on the 29th of March 1843, the Resident Engineer had the satisfaction of finding the whole building perfectly water-tight and saw not the slightest trace of a defective joint. Concluding works on the Rock, such as pointing, &c. The outside joints of the building were therefore carefully “ripped,” and repointed with mortar, composed of equal parts of Halkin lime and Pozzolano. That operation, from the difficulty of employing many men, where suspended scaffolds[175] were necessary and from the care with which it requires to be executed, occupied a great deal of time.
Another tedious operation was the Interior fittings of the Tower. fitting up of the interior of the Tower with wainscot lining and forming the various stories into apartments separate from the staircase. Much work was also expended in providing the fire-places with proper flues, in fitting up water tanks, coal stores, and oil tanks, and also in conveying the air-tubes between the Lightroom and the several apartments by which the signal bells are rung for summoning the keepers to mount guard. The keeper on duty is, by the rules of the Service, forbidden, under penalty of instant dismissal, to leave the Light-room, on any pretext, until relieved by the next who mounts guard, and who is summoned by means of a bell placed inside his cot or sleeping berth, which is rung by means of a small piston, propelled by simply blowing into a mouth-piece in the Light-room. The keeper in bed answers this signal by a “counter-blast,” which rings another bell in the Light-room, and informs the keeper there that his signal has been heard and will be obeyed.
Arrangement of the several apartments. The general arrangement of the Tower, may be seen in the Section Plate VIII.; and the details of its subdivision are very similar to those shewn in Plate XVI. of my Father’s Account of the Bell Rock Lighthouse. The ascent to the outside door is by a ladder or trap of gun metal, 26 feet high. The first apartment on the level of the entrance door, is chiefly appropriated to the reception of iron water-tanks, capable of holding a supply of 1251 gallons. The next story is set aside for coals, which are stowed in large iron boxes. The third apartment is a workshop; the fourth is the provision store; and the fifth is the kitchen. Above are two stories, each divided into two sleeping apartments, for the four Light-keepers. Over them is the room for the Visiting Officers; then follows the oil store, and lastly comes the Lightroom, making in all twelve apartments. The nearness of the oil store to the Lightroom is a great convenience to the Keepers, who are thus saved the trouble of carrying the daily supply of oil[176] to the Lightroom, up a long flight of steps. The passage from story to story is by oaken trap ladders, passing through hatches in each floor and partitioned off from each apartment in order to prevent accidents and to check cold draughts.
Lightroom Apparatus, and first exhibition of the Light. The light of Skerryvore was exhibited to the mariner on the night of the 1st February 1844, in terms of the Statutory Notice, which will be found in the Appendix. The light is revolving, appearing in its brightest state once in every minute of time. It is elevated 150 feet above the sea, and is well seen as far as the curvature of the earth permits; it is also frequently seen as a brilliant light from the high land of Barra, a distance of 38 miles. The apparatus consists of eight annular lenses (of the first order, in the system of Augustin Fresnel), of 36·22 inches focal distance, revolving round a lamp with four concentric wicks, and producing a bright blaze when each lens passes between the lamp and the eye of a distant observer. Above those lenses are placed eight pyramidal lenses of 19·68 inches focal distance, inclined at 50° with the horizon and combined with eight plane mirrors, inclined in the opposite direction at 50° with the horizon. By this arrangement, that part of the light from the lamp which would otherwise escape uselessly beyond the great lenses, upwards into the sky, being parallelized in its passage through the smaller lenses and falling on the mirrors, is finally projected forwards in horizontal beams, so as to aid the effect of the light. Those lenses and mirrors, however, instead of having their axes in the same vertical plane with the axes of the principal lenses, are inclined about 7° horizontally to the right hand, and by that deviation produce small premonitory blazes, which, blending with the beams of the larger lenses, tend in some measure to lengthen the duration of the impression on the eye. So far the apparatus of the Skerryvore Lighthouse is identical in its general arrangements with that of the Tour de Corduan, and differs only in the superior workmanship of the lenses and the machinery, which the experience of more than twenty years has brought about, since Fresnel[177] designed that light in 1822. Instead, however, of employing curved mirrors, as has been done at Corduan, to collect the light which would otherwise escape below the lenses and, at the same time, to send it to the horizon, I determined to put in practice a plan which I had long contemplated, of placing totally reflecting zones below the lenses, similar in construction to the zones of the small Harbour Light Apparatus of the fourth order, which was also invented by Fresnel. This was finally carried into effect, agreeably to the design of M. Leonor Fresnel, his brother, with whom I had corresponded on the subject. In the subsequent pages of this volume, I intend to make some observations explanatory of the principles and arrangement of the various optical instruments employed in Lighthouses; and as that will afford me a more convenient opportunity of describing the nature and properties of the totally reflecting zones, I shall forbear in this place to enter into further details as to the construction or action of the apparatus at the Skerryvore. It is right, however, that I should mention here that the lenses, mirrors and zones are from the works of M. François of Paris, whose name I shall afterwards have occasion to notice; and that the machinery was constructed to my entire satisfaction, and in a manner worthy of his reputation as a mechanician, by Mr John Milne of Edinburgh.
In such a situation as the Skerryvore, new wants were discovered every day; and each summer brought its round of smaller works, which the experience of the preceding winter had suggested. The Barrack was found very useful as a place of residence for the workmen, who were engaged in such needful works; and it was not until the summer of 1846, Removal of the Barrack from the Rock. that it was taken to pieces and removed from the Rock, after having kept its place for six years. Its removal, however, was then thought advisable, as some of its fixtures, by the continual action of the weather, had become very loose and precarious; and, although a very small outlay would have made it almost as stable as at first, it was considered inexpedient to attempt to perpetuate a structure confessedly[178] temporary in its nature, and the sudden destruction of which by the waves, seemed to involve some risk of injury to the Tower itself.
Expense. The expense of erecting the Skerryvore Lighthouse, including the opening of quarries and forming wharfs at the quarries in Mull and also the Harbour in Tyree, was, as appears from the Account in the Appendix, L.86,977 : 17 : 7.
In the course of the Summer of 1844, a marble tablet, bearing an inscription in letters of gold, was, by order of the Commissioners, placed over one of the windows in the Visiting Officers’ Room. With a representation of the Tablet and the Inscription, which, after acknowledging the hand of Almighty God in the success which attended the work, briefly sets forth the beneficent purposes for which the Lighthouse was erected and records the laying of the foundation-stone by his Grace the Duke of Argyll, I willingly close this most defective narrative of the work.

Engraved by W. & A.K. Johnston
IN SALUTEM OMNIUM
NORTHERN LIGHTHOUSES
A. D. O. M.
AUCTORITATE . ET . CONCILIIS
PHARORUM . SCOTIAE . COLLEGII
HAEC . STRUCTA . FUIT . PHAROS
CUJUS . DIRECTI . FLAMMA
NAUTAE
INFAMIBUS . HIS . SCOPULIS . ADHUC . MERITO . DETERRITI
OPTATUM . PORTUM . RECTIUS . ADVENIRENT.
JOANNES . DUX . DE . ARGYLL
INSULARUM . ADJACENTIUM . DOMINUS
LAPIDEM . AUSPICALEM . RITE . STATUIT
DIE . IV . MENSIS . JULII . ANNO . IV . VICT. REG.
M . D . C . C . C . X . L .
OPERUM . MAGISTRO . ALANO . STEVENSON . L.L.B.
[179]
PART SECOND.
NOTES
ON THE
ILLUMINATION OF LIGHTHOUSES.
Early History. The early history of Lighthouses is very uncertain; and some ingenious antiquaries, finding the want of authentic records, have been anxious to supply the deficiency by conjectures based upon casual and obscure allusions in ancient writers, and by vague hypotheses drawn from the heathen mythology. Some writers have gone so far as to imagine, that the Cyclopes were the keepers of lighthouses; whilst others have actually maintained that Cyclops was intended, by a bold prosopopœia, to represent a lighthouse itself.[24] A notion so fanciful deserves little consideration; and accords very ill with that mythology of which it is intended to be an exposition, as seems sufficiently plain from a passage in the ninth Odyssey, where Homer (who flourished about 907 B. C.), after describing the darkness of the night, informs us that the fleet of Ulysses actually struck the shore of the Cyclopean island, before it could be seen.[25]
[24] This spirit of etymological conjecture has converted Cyclops, Proteus, Cneph, Phanes, Canobus, Chiron, Tithonus, Thetis, Amphitrite, Minotaurus, Chronus, Phrontis, and other demigods, into celebrated lighthouses, or, at all events, has imagined that those mythological personages were worshipped under the emblem of fire or light in buildings, which, at the same time, served as guides to the benighted mariner. On the faith, also, of similar obscure and finely drawn etymologies, various places, such as Calpe and Abyla, the opposite points of Africa and Europe, at the Straits of the Mediterranean, have been unhesitatingly recognized as the sites of celebrated light-towers; and the Latin words turris and columna have been supposed primarily to signify a lighthouse, the first being written Tor-is, the Tower of fire, and the Col-on, the Pillar of the Sun.
Odyss., ix., 146.
[182]
Nor does there appear any better reason for supposing, that under the history of Tithonus, Chiron, or any other personage of antiquity, the idea of a lighthouse was conveyed; for such suppositions, however reconcileable they may appear with some parts of mythology, involve obvious inconsistencies with others. It seems, indeed, most improbable, that, in those early times, when navigation was so little practised, the advantages of beacon lights were so generally known and acknowledged as to render them the objects of mythological allegory.
It must not, however, be imagined, that ancient writings are entirely destitute of allusions to the subject of Beacon Lights for the guidance of the Mariner. The venerable poet, already noticed, in speaking of the shield of Achilles, has beautifully described the flash of a beacon-light in some solitary place, as seen by seamen leaving their friends, in those lines, which contain ample proof of the existence of such a provision for the safety of the mariner in Homer’s time:—
Il., xix., 375.
In the Holy Scriptures the word Beacon occurs but once, and that in Prophecies of Isaiah (xxx. 17.), who lived above 200 years later than Homer; but it is obvious that the original term, which the Septuagint translate by the word ἱστος, merely imports a flagstaff or perch and does not at all imply the knowledge of beacon-lights among the Hebrews, who were not a maritime people.
Colossus of Rhodes. About 300 years before the Christian era, Chares, the disciple of Lysippus, constructed the celebrated brazen statue, called the Colossus of Rhodes. It was of such dimensions as to allow vessels to sail into the harbour between its legs, which spanned[183] the entrance. There is considerable probability in the idea that this figure served the purposes of a lighthouse; but there is no passage in any ancient writer, where this use of the Colossus is expressly mentioned. Many inconsistencies occur in the account of this fabric by early writers, who, in describing the distant objects which could be seen from it, appear to have forgotten the height which they assign to the figure. It was partly demolished by an earthquake, about eighty years after its completion; and so late as the year 672 of our era, the brass of which it was composed was sold by the Saracens to a Jewish merchant of Edessa, for a sum, it is said, equal to L.36,000.
Pharos of Alexandria. Little is known with certainty regarding the Pharos of Alexandria, which was regarded by the ancients as one of the seven wonders of the world. It was built in the reign of Ptolemy Philadelphus, about 300 years before the Christian era; and Strabo relates that Sostratus, a friend of the royal family, was the architect. He describes it as built in a wonderful manner in many stories of white stone, on a rock forming the promontory of the island Pharos (whence the Tower derived its name), and says that the building bore the inscription—“Sostratus of Cnidos, the son of Dexiphanes, to the Gods, the Saviours, for the benefit of seamen.” He concludes his brief notice of it by describing the neighbouring shores as low and encumbered with shoals and snares, and as calling for the establishment of a lofty and bright beacon, a sign to guide sailors arriving from the ocean into the entrance to the haven.[26]
[26] The passage from which the above description is drawn will be found in the Oxford edition of Strabo, 1807, page 1123. It is as follows: Ἔστι δε και ἀυτο τὸ τῆς νησίδος ἄχρον πετρα πολυκλύστος, ἔχουσα πῦργον θαυμαστῶς κατεσκευασμένον λευκου λιθου, πολυοροφον, ὁμωνυμον τῇ νὴσῳ· τουτον δε ἄνέθηκε Σωστρατος Κνὶδιος φιλος τῶν βασιλεων, της των πλωϊζομενων σωτηριας χαριν, ὥς φησιν ἥ ἐπιγραφη Επιγραμμα, ΣΩΣΤΡΑΤΟΣ ΚΝΙΔΙΟΣ ΔΕΧΙΦΑΝΟΥΣ, ΘΕΟΙΣ ΣΩΤΗΡΣΙΝ ΥΠΕΡ ΤΩΝ ΠΑΩΙΖΟΜΕΝΩΝ. Ἀλιμένου γαρ ὄυσης και ταπεινῆς της ἕκατέρωθεν παραλίας, ἐχουσης δε και χοιράδας και βράχη τινὰ, ἔδει σημεὶου τινος ὑψηλου και λαμπρου, τοις ἀπὸ του πελάγους προσπλέουσιν, ὥστ’ ἐυστοχειν της ἐισβολης του λιμενος. Strabo’s account of the position of the island of Pharos at once leads to the conclusion of its having formed part of the harbour of Alexandria (as is abundantly testified by Josephus, Pliny, and other writers), and cannot be easily reconciled with that of Homer (fourth Odyssey, l. 354), who describes the island as a day’s sail with a fair wind from the mainland. His words are as follows:—
Odyssey, iv., l. 354.
Pliny, however, does not scruple to identify the Pharos of Homer’s time with that of his own day. “Pharos,” says he, “quondam diei navigatione distans ab Ægypto, nunc è turri nocturnis ignibus cursum navium regens.” Hist. Nat., v. 31; see also Hist. Nat., ii. 87, and xiii. 21.
[184]
The accounts which have come down to us of the dimensions of this remarkable edifice are exceedingly various; and the statements of the distance at which it could be seen are clearly fabulous. That of Josephus (who likens it to the second of Herod’s three Towers at Jerusalem, called Phasael, in honour of his brother) is the least removed from probability; yet even he informs us, that the fire which burnt on the top to enable seamen to anchor in sight of it, before coming near the shore, and so to avoid the difficulty of the navigation by night, was visible at a distance equal to about thirty-four English miles. Such a range for a lighthouse on the low shores of Egypt, would require a tower about 550 feet in height![27] Ammianus Marcellinus[28] and Pliny[29] are both very circumstantial[185] in their notices of the Pharos as a beacon-light to guide seamen in approaching the coast of Egypt and port of Alexandria. The latter adds the interesting fact, that the cost of the Tower was reckoned at a sum equal to about L.390,000 of our money;[30] and both of them agree in stating that a light was shewn from it at night. Ammianus Marcellinus differs from all the other writers, in attributing the erection of the Tower to Queen Cleopatra. Pliny mentions in passing, that there were also lighthouses at Ostia and Ravenna.
[27] Bell. Judaic. iv., cap. 10, sec. 5. (Havercamp’s Josephus, tom. ii., p. 309. Amsterdam, 1726.) ἐν δεξιᾳ δε ἡ προσαγορευομενη Φαρος νησις προκειται, πῦργον ανἐχουσα μεγιστον, εκπυρσευοντα τοις καταπλὲουσιν, ἐπι τριακοσιους σταδιους, ὤς ἐν νυκτὶ πὂρρωθεν ὁρμιζοιντο προς την δυσχέρειαν του καταπλοῦ. And again, in the sixth Book of the same History (v. 4, sec. 3, tom. ii., p. 330), he says, και τὸ μεν σχημα παρεῴκει τῳ κατα τὴν Φαρον ἐκπυρσεὐοντι τοις επ’ Αλεξανδρείας πλέουσι. The height of the Tower in the text proceeds on the idea of the observer’s eye being ten feet above the sea.
[28] Ammianus Marcellinus, l. xxii., c. 16. (Leipsic 1807, tom. i., p. 306.) Hoc littus cum fallacibus et insidiosis accessibus affligeret antehac navigantes discriminibus plurimis, excogitavit in portu Cleopatra turrim excelsam, quae Pharos a loco ipso cognominatur, praelucendi navibus nocturna suggerens ministeria; cum, quondam ex Parthenio pelago venientes aut Libyco, per pandas oras et patulas, montium nullas speculas vel collium signa cernentes, harenarum inlisae glutinosae mollitiae frangerentur.
[29] Plinii Hist. Nat., xxxvi. 18. (Paris, 1723, p. 739.) Magnificatur et alia turris a rege facta in insula Pharo portum obtinente Alexandriae, quam constitisse octingentis talentis tradunt; magno animo (nequid omittamus) Ptolemai regis, quod in ea permiserit Sostrati Guidii Architecti structuræ ipsius nomen inscribi. Usus ejus, nocturno navium cursu ignes ostendere ad praenuncianda vada portûsque introïtum: quales, jam compluribus locis flagrant, ut Ostiae ac Ravennae. Periculum in continuatione ignium, ne sidus existimetur, quoniam è longinquo similis flammarum aspectus est.
[30] Supposing, as is most probable, that Pliny means the Egyptian talent; the Attic talent was about one-half the value of the other.
If the reports of some writers are to be believed, this Tower must have far exceeded in size the great Pyramid itself; but the fact that a building of comparatively so late a date should have so completely disappeared, whilst the Pyramid remains almost unchanged, is a sufficient reason for rejecting, as erroneous, the dimensions which have been assigned by most writers to the Pharos of Alexandria. Some have pretended that large mirrors were employed to direct the rays of the beacon-light on its top, in the most advantageous direction; but, in so far as I know, there is no definite evidence in favour of this supposition. Others, with greater probability, have imagined that this celebrated beacon was known to mariners, simply by the uncertain and rude light afforded by a common fire. In speaking of the Pharos, the poet Lucian, on most occasions sufficiently fond of the marvellous, takes no notice of the gigantic mirrors which it is said to have contained. He thus speaks of this celebrated lighthouse as having indicated to Julius Cæsar his approach to the Pharos of Egypt on the seventh night after he sailed from Troy:
Pharsal., ix., 1004.
[186]
It is true that, by using the word “lampada,” which can only with propriety be applied to a more perfect mode of illumination than an open fire, he appears to indicate that the “flammis” of which he speaks, were not so produced. The word lampada may however, be used metaphorically; and flammis would, in this case, not improperly describe the irregular appearance of a common fire.
Perhaps, also, the opinion that some kind of lamp was used in the Pharos, may seem to receive countenance from the remarkable words of Pliny, in the passage above cited—“Periculum in continuatione ignium, ne sidus existimetur, quoniam è longinquo similis flammarum aspectus est.” The fear he expresses lest the light viewed from a distance should be mistaken for a star, could hardly be applicable to the diffuse, oscillating, lambent light derived from an open fire, and certainly gives some reason for imagining that, even at that remote time, the art of illuminating lighthouses was better understood than in the early part of the present century.
Before leaving the subject of the Pharos of Alexandria, I wish to vindicate the memory of its architect Sostratus from the calumny of Lucian, who, in his Treatise on the art of writing history, with his usual acrimony, accuses the builder of the Pharos of a fraud, in cutting his own name on the solid walls of the Tower, and covering the inscription with plaster, on which he carved the name of his royal master Ptolemy.[31] Against this assertion I would oppose the testimony of Strabo, who calls Sostratus the “friend of the Kings” (see the quotation at the foot of page 183), and the direct evidence of Pliny, who, in the passage above cited, expressly states, as a proof of Ptolemy’s magnanimity, his giving the architect liberty[187] to inscribe his own name on the Tower. The only other notices of the Pharos which I have been able to find in ancient writers are from Cæsar’s Commentaries, Valerius Flaccus, and Pomponius Mela.[32] At Alexandria, there is a modern lighthouse called the Pharos, which is maintained by the Pacha of Egypt.
[31] Lucian, in his Treatise (Amsterdam, 1743, vol. ii., p. 68.) Πως δει ἱστοριαν συγγραφειν, thus details the merit and fraud of Sostratus. Ορᾷς τον Κνίδιον ἐκεῖνον ἀρχιτεκτονα, οἶον ἐποίησεν; οἰκοδομὴσας γαρ τον ἐπὶ τῇ Φαρῳ πῦργον, μεγιστον και καλλιστον ἔργων ἀπαντων, ὡς πυρσεύοιτο ἀπ’ αὐτου τοις ναυτιλλομενοις, ἐπὶ πολὺ της θαλασσης, και μὴ καταφέροιντο εἰς την Παραιτονίαν, παγχάλεπον, ὣς φασιν, οὖσαν και ἄφυκτον, εἴ τις ἐμπεσοι εἴς τα, ἕρματα. Οἰκοδομήσας οὐν το ἔργον, ἔνδοθεν μεν, κατα των λιθων, το αὐτου ὄνομα ἐπέγραψεν. Ἐπιχρίσας δὲ τιτάνῳ και ἐπικαλύψας, ἐπέγραψε το ὀνομα του τότε βασιλέυοντος, εἰδὼς, ὃσπερ και ἐγενετο, πάνυ ὀλιγου χρονου, συνεκπεσουμενα μεν τῳ χρισματι τα γραμματα, εκφανησόμενον δε ΣΩΣΤΡΑΤΟΣ ΔΕΧΙΦΑΝΟΥΣ Κνιδιος. θεοις σωτηρσιν ὑπερ των πλωΐζομεων, κ.τ.λ.
[32] Cæsar de Bell. Civil., iii. 98 (Lond. 1712, p. 355). Pharus est in insula turris, magna altitudine, mirificis operibus extructa, quae nomen ab insula accepit.
Valerius Flaccus very distinctly sets forth the great advantage of lighthouses to the seaman, and especially speaks of those at Alexandria and Ostia in these lines—
Argonaut, vii., v. 84.
Pompon. Mela, ii. cap. 7.
Coruña Tower Mr Moore, in his History of Ireland, vol. i., p. 16, speaks of the Tower of Coruña, which he says is mentioned in the traditionary history of that country, as a lighthouse erected for the use of the Irish in their frequent early intercourse with Spain. In confirmation of this opinion, he cites a somewhat obscure passage from Æthicus, the cosmographer. This in all probability is the tower which Humboldt mentions in his Narrative under the name of the Iron Tower, which was built as a lighthouse by Caius Saevius Lupus, an architect of the city of Aqua Flavia, the modern Chaves.[33] [188] A Lighthouse has lately been established on this headland, for which Dioptric apparatus was supplied from the workshop of M. Letourneau of Paris.
[33] “The traditionary history,” says Mr Moore, “of the latter country (Ireland) gives an account of an ancient Pharos or lighthouse erected in the neighbourhood of the port now called Coruña, for the use of navigators on their passage between that coast and Ireland. There is a remarkable coincidence between this tradition and an account given by Æthicus, the cosmographer, of a lofty Pharos or lighthouse standing formerly on the sea-coast of Gallicia, and serving as a beacon in the direction of Britain. Secundus Angulus intendit ubi Brigantia civitas sita est Galliciae, et altissimum Pharum et inter pauca memorandi operis ad speculum Britanniae. Whether the translation I have given of the last three words of this passage convey their real meaning, I know not; but they have been hitherto pronounced unintelligible. The passage is thus noticed by Casaubon, in a note on Strabo, lib. iii. ‘Æthicus in Hispaniae descriptione altissimi cujusdam Fari meminit.’” The passage in Strabo above referred to is on page 179 of the first volume of the Oxford folio edition of 1807, where the geographer speaks of Cape Νεριον, which Casaubon distinctly identifies with the Cabo de Finisterra of modern seamen.
There is also a record in Strabo of a magnificent lighthouse of stone at Lighthouse at the mouth of the Guadalquivir. Capio, or Apio, near the Harbour of Menestheus (the modern Mesa Asta, or Puerto de Sta. Maria), which he describes as built on a rock nearly surrounded by the sea, as a guide for the shallows at the mouth of the Guadalquivir, in terms almost identical with those used by him in speaking of the Pharos of Alexandria. I am not aware of any other notice of this great work, for such it seems to have been, to have deserved the praises of Strabo.[34]
[34] The words of Strabo are (Oxon. 1807, p. 184), Και ὁ του Καπὶωνος (vel Ἀπιωνος) πὺργος ἵδρυται ἐπι πέτρας ἀμφκλυστου, θαυμασιως κατεσκευασμένος, ὥσπερ ό Φαρος τῆς των πλωϊζομενων σωτηριας χαριν, ῃ τε γαρ ἐκβαλλομενη χους ὕπο του ποταμου βραχεα ποιει και χοιραδωδης ἐστὶν ὁ πρὸ ἀυτου τοπος ὥστε δει σημειου τινος ἐπιφανοῦς.
Ancient Phari in Britain. In Camden’s Britannia, a passing notice is taken of the ruins called Cæsar’s Altar, at Dover, and of the Tour d’Ordre, at Boulogne, on the opposite coast; both of which are conjectured to have been ancient lighthouses. Pennant describes the remains of a Roman Pharos near Holywell, but cites no authorities for his opinion as to its use. There were likewise remains of a similar structure at Flamborough-head. A very meagre and unintelligible account is also given of a lighthouse at St Edmund’s Chapel, on the coast of Norfolk, in Gough’s additions to Camden, by which it might seem that the lighthouse was erected in 1272.[35]
[35] Gough’s Camden’s Britannia, vol. i., 318, and vol. ii., p. 198; Batcheller, in his Dover Guide (1845, p. 111), says, that the Dover Pharos was built “during the lieutenancy of Aulus Plautius and Ostorius Scapula, the latter of whom left Britain, A. D. 53.”—Pennant’s History of Whiteford and Holywell, p. 112.
Such seems to be the sum of our knowledge of the ancient history of lighthouses, which, it must be admitted, is neither accurate nor extensive. Our information regarding modern lighthouses is of course more minute in its details and more worthy of credit. The greater part of it is drawn from authentic sources; and much[189] of what is afterwards stated is the result of my own observation, during my visits to the most important lighthouses of Europe.
The first lighthouse of modern days that merits attention, is the Tour de Corduan. Tour de Corduan, which, in point of architectural grandeur, is unquestionably the noblest edifice of the kind in the world. It is situated on an extensive reef at the mouth of the river Garonne, and serves as a guide to the shipping of Bordeaux and the Languedoc Canal, and indeed of all that part of the Bay of Biscay. It was founded in the year 1584, but was not completed till 1610, under Henri IV. It is minutely described in Belidor’s Architecture Hydraulique. The building is 197 feet in height, and consists of a pile of masonry, forming successive galleries, enriched with pilasters and friezes, and rising above each other with gradually diminished diameters. Those galleries are surmounted by a conical tower, which terminates in the lantern. Round the base is a wall of circumvallation, 134 feet in diameter, in which the light-keepers’ apartments are formed, somewhat in the style of casemates. This wall is an outwork of defence, and receives the chief shock of the waves. The tower itself contains a chapel, and various apartments; and the ascent is by a spacious staircase. The first light exhibited in the Tour de Corduan was obtained by burning billets of oak-wood, in a chauffer at the top of the tower; and the use of coal instead of wood, was the first improvement which the light received. A rude reflector, in the form of an inverted cone, was afterwards added, to prevent the loss of light which escaped upwards. About the year 1780, M. Lenoir was employed to substitute paraboloïdal reflectors and lamps; and in 1822, the light received its last improvement, by the introduction of the dioptric instruments of Augustin Fresnel, the celebrated French Academician.
Eddystone. The history of the famous Lighthouse on the Eddystone Rocks is well known to the general reader, from the narrative of Smeaton the Engineer. Those Rocks are 9¹⁄₂ miles from the Ram-Head, on the coast of Cornwall; and from the small extent of the[190] surface of the chief Rock and its exposed situation, the construction of the Lighthouse was a work of very great difficulty. The first erection was of timber, designed by Mr Winstanley; and was commenced in 1696. The light was exhibited in November 1698. It was soon found, however, that the sea rose upon that tower to a much greater height than had been anticipated; so much so, it is said, as to “bury under the water” the lantern, which was sixty feet above the Rock; and the Engineer was therefore afterwards under the necessity of enlarging the Tower, and carrying it to the height of 120 feet. In November 1703, some considerable repairs were required, and Mr Winstanley, accompanied by his workmen, went to the Lighthouse to attend to their execution; but the storm of the 26th of that month, carried away the whole erection, when the Engineer and all his assistants unhappily perished!
The want of a light on the Eddystone, soon led to a fatal accident; for not long after the destruction of Mr Winstanley’s lighthouse, the Winchilsea man-of-war was wrecked on the Eddystone Rocks, and most of her crew were lost. Three years, however, elapsed, after this melancholy proof of the necessity for a light, before the Trinity-House of London could obtain a new Act of Parliament, to extend their powers; and it was not till the month of July 1706, that the construction of a new lighthouse was begun under the direction of Mr John Rudyerd of London. On the 28th of July 1708, the new light was first shewn, and it continued to be regularly exhibited till the year 1755, when the whole fabric was destroyed by accidental fire, after it had stood forty-seven years. But for this circumstance, it is impossible to tell how long the lighthouse might, with occasional repair, have lasted, as Mr Rudyerd seems to have executed his task with much judgment, carefully rejecting all architectural decoration, as unsuitable for such a situation, and directing his attention to the formation of a tower which should offer the least resistance to the waves. The height of the tower, which was of a conical form and constructed of timber, was 92 feet, including the lantern; and the diameter at[191] the base, which was a little above the level of high water, was 23 feet.
The advantages of a light on the Eddystone having been so long known and acknowledged by seamen, no time was permitted to elapse before active measures were taken for its restoration; and Smeaton, to whom application was made for advice on the subject, recommended the exclusive use of stone as the material, which, both from its weight and other qualities, he considered most suitable for the situation. On the 5th of April 1756, Smeaton first landed on the Rock and made arrangements for erecting a Lighthouse of stone and preparing the foundations, by cutting the surface of the rock into regular horizontal benches, into which the stones were carefully dovetailed or notched. The first stone was laid on 12th June 1757 and the last on the 24th of August 1759. The Tower measures 68 feet in height and 26 feet in diameter at the level of the first entire course; and the diameter under the cornice is 15 feet. The first 12 feet of the Tower form a solid mass of masonry; and the stones of which it is composed are united by means of stone joggles, dovetailed joints, and oaken treenails. It is remarkable that Smeaton should have adopted an arched form for the floors of his building, instead of employing the floors as tie-walls formed of dovetailed stones. To counteract the injurious tendency of the outward thrust of those arched floors, he had recourse to the ingenious expedient of laying, in circular trenches or grooves cut in the stones which form the outside casing, tie-belts of chain, which were heated before being set in the grooves by means of an application of hot lead and became tight in cooling, after they were fixed in the wall. The light was exhibited on the 16th October 1759; but such was the state of lighthouse apparatus in Britain at that period, that a feeble light from tallow candles was all that decorated this noble structure. In 1807, when the property of this lighthouse again came into the hands of the Trinity-House, at the expiry of a long lease, Argand burners, and paraboloïdal reflectors of silvered copper, were substituted for the chandelier of candles.
[192]
Bell Rock. The dangerous reef called the Inch Cape, or Bell Rock, so long a terror to mariners, was well known to the earliest navigators of Scotland. Its dangers were so generally acknowledged, that the Abbots of Aberbrothwick, from which the Rock is distant about twelve miles, caused a float to be fixed upon the Rock with a bell attached to it, which being swung by the motion of the waves, served by its tolling to warn the mariner of his approach to the reef. From this circumstance, which formed the groundwork of Southey’s striking ballad of Sir Ralph the Rover, the Rock is said to have derived its name. Amongst the many losses which occurred on the Bell Rock in modern times, one of the most remarkable is that of the York, seventy-four, with all her crew, part of the wreck having been afterwards found on the Rock and part having come ashore on the neighbouring coast. During the survey of the Rock also, several instances were discovered of the extent of loss which this reef had occasioned; and many articles of ships’ furnishings were picked up on it, as well as various coins, a bayonet, a silver shoe-buckle, and many other small objects. Impressed with the great importance of some guide for the Bell Rock, Captain Brodie, R.N., set a small subscription on foot and erected a beacon of spars on the Rock, which, however, was soon destroyed by the sea. He afterwards constructed a second beacon, which soon shared the same fate. It was not, therefore, until 1802, when the Commissioners of Northern Lights brought a bill into Parliament for power to erect a lighthouse on it, that any efficient measures were contemplated for the protection of seamen from this Rock, which, being covered at every spring-tide to the depth of from twelve to sixteen feet, and lying right in the fairway to the Friths of Forth and Tay, had been the occasion of much loss both of property and life. In 1806, the bill passed into a law; and various ingenious plans were suggested for overcoming the difficulties which were apprehended, in erecting a lighthouse on a rock twelve miles from land, and covered to the depth of twelve feet by the tide. But the suggestion of Mr Robert Stevenson,[193] the Engineer to the Lighthouse Board, after being submitted to the late Mr Rennie, was at length adopted; and it was determined to construct a tower of masonry, on the principle of the Eddystone. On the 17th of August 1807, Mr Stevenson accordingly landed with his workmen and commenced the work by preparing the Rock to receive the supports of a temporary pyramid of timber, on which a barrack-house for the reception of the workmen (similar to that which has already been described in a preceding part of this volume) was to be placed; and during this operation, much hazard was often incurred in transporting the men from the Rock, which was only dry for a few hours at spring-tides, to the vessel which lay moored off it. The lowest floor of this temporary erection, in which the mortar for the building was prepared, was often broken up and removed by the force of the sea. The foundation for the tower having been excavated, the first stone was laid on the 10th July 1808, at the depth of sixteen feet below the high water of spring-tides; and at the end of the second season, the building was five feet six inches above the lowest part of the foundation. The third season’s operations terminated by finishing the solid part of the structure, which is thirty feet in height; and the whole of the masonry was completed in October 1810. The light was first exhibited to the public on the night of the 1st of February 1811. The difficulties and hazards of this work were chiefly caused by the short time during which the Rock was accessible between the ebbing and flowing tides; and amongst the many eventful incidents which render the history of this work interesting, was the narrow escape which the Engineer and thirty-one persons made from being drowned, by the rising of the tide upon the Rock, before a boat came to their assistance, at a time when the attending vessel had broken adrift. This circumstance occurred before the Barrack-house was erected, and is narrated by Mr Stevenson, in his Account of the work, published at the expense of the Lighthouse Board in 1824, to which I would refer for more minute information[194] on the subject of this work and the other lighthouses on the coast of Scotland.
The Bell Rock Tower is 100 feet in height, 42 feet in diameter at the base, and 15 at the top. The door is 30 feet from the base and the ascent is by a massive copper ladder. The apartments, including the light-room, are six in number. The light is a revolving red and white light; and is produced by the revolution of a frame containing sixteen Argand lamps, placed in the foci of paraboloïdal mirrors, arranged on a quadrangular frame, whose alternate faces have shades of red glass placed before the reflectors, so that a red and white light is shewn successively. The machinery, which causes the revolution of the frame containing the lamps, is also applied to tolling two large bells, to give warning to the mariner of his approach to the Rock in foggy weather. The erection of the Bell Rock Lighthouse cost L.61,331 : 9 : 2.
Carlingford. The most remarkable Lighthouse on the coast of Ireland is that of Carlingford, near Cranfield Point, at the entrance of Carlingford Lough. It was built according to the design of Mr George Halpin, the Inspector of the Irish Lights; and was a work of an arduous nature, being founded 12 feet below the level of high-water, on the Hawlbowling Rock, which lies about two miles off Cranfield Point. The figure of the Tower is that of a frustum of a cone, 111 feet in height, and 48 in diameter at the base. The light, which is fixed, is from oil burned in Argand lamps, placed in the foci of paraboloïdal mirrors. It was first exhibited on the night of December 20, 1830.
There are various other Lighthouses, which, in themselves, are sufficiently deserving of a separate notice, were it not that they have more or less something in common with those already described, which are unquestionably the most remarkable edifices of the kind. The first design for an Iron Lighthouses. Iron Lighthouse, is that by my Father for the Bell Rock, in the year 1800. The invention of Mr Mitchell of Belfast, for applying the principle of the screw to the erection of Lighthouses on soft foundations, deserves a longer notice than is consistent with the nature of these notes.[195] It must therefore be sufficient to say, that the principal Lighthouses on this plan (those of the Maplin, Fleetwood, and Belfast Lough) consist of piles or of hollow pillars of cast-iron, grouped together in the form of a truncated pyramid, and closely resembling, in the general arrangement of their parts, the Beacon shewn in Plate XXX., and that erected on the Carr Rock in 1821. The lower end of each pillar is furnished with a flat screw or worm and a sharp point, which is screwed into the sand, clay, or gravel, or other soft subsoil. Mr Alexander Gordon of London also fitted up a Lighthouse, composed of cast-iron plates, which was erected at Morant, in the West Indies, a style of building in itself by no means eligible, and which seems suitable only where stone cannot be easily obtained, or conveniently applied. Both those plans (except in so far as the screw is concerned, which is indeed the distinguishing feature of Mr Mitchell’s ingenious plan) are to be found in one of my Father’s designs for the Bell Rock Lighthouse (see his Account, at Plate VII., figs. 2, 3, 4, and 5, and pp. 499, 500). Dr Potts has also invented a method of driving piles by means of atmospheric pressure, which has been used at the South Galliper Beacon, on the Goodwin Sands.
Having thus hastily described the most interesting and celebrated Lighthouses, I proceed to the proper object of these Notes, which are chiefly intended to make known the various methods now in use for the illumination of Lighthouses. There can be little doubt, that down to a very late period, Early modes of Illumination. the only mode of illumination adopted in the Lighthouses, even of the most civilized nations of Europe, was the combustion of wood or coal in chauffers, on the tops of high towers or hills. It consists with the personal knowledge of many persons now living, that the Isle of May Light, in the Frith of Forth, previous to its being assumed by the Commissioners of the Northern Lights in 1786, was of that kind; and, even in England, the art of illumination had made so little progress, that the magnificent Tower of the Eddystone, for about forty years after it came from the hands of Smeaton, could boast of no[196] better Light than that derived from a few miserable tallow candles. Such methods were most imperfect, not only in point of efficiency and power, but also as respects the distinction of one light from another, an object which, on a difficult and rugged coast, may be considered as of almost equal importance with the distance at which the Light can be seen.
Solid substances which remain so throughout their combustion, are only luminous at their own surface, and exhibit phenomena, such as the dull red heat of iron, or of most kinds of pit-coal, and are therefore more suited for the purpose of producing heat than light. But by using substances which are formed into inflammable vapours, at a temperature below that which is required for the ignition of the substances themselves, gas is obtained and Flame. flame is produced. Much light is thus evolved at a comparatively low temperature. The gas necessarily rises above the combustible substance from which it is evolved, owing to its being formed at a temperature considerably higher than that of the surrounding air, than which it is necessarily rarer. Of this description are the flames obtained by the burning of the various oils, which are generally employed in the illumination of lighthouses. In the combustion of oil, wicks of some fibrous substance, such as cotton, are used, into which the oil ascends by capillary action, and being supplied in very thin films, is easily volatilized into vapour or gas by the heat of the burning wick. The gas of pit-coal has been occasionally used in lighthouses; it is conveyed in tubes to the burners, in the same manner as when employed for domestic purposes. There are certain advantages, more especially in dioptric lights, where there is only one large central flame, which would render the use of gas desirable. The form of the flame, which is an object of considerable importance, would thus be rendered less variable, and could be more easily regulated, and the inconvenience of the clock-work of the lamp would be wholly avoided. But it is obvious, that gas is by no means suitable for the majority of lighthouses, their distant situation and generally difficult access[197] rendering the transport of large quantities of coal expensive and uncertain; whilst in many of them there is no means of erecting the apparatus necessary for manufacturing gas. There are other considerations which must induce us to pause before adopting gas as the fuel of lighthouses; for, however much the risk of accident may be diminished in the present day, it still forms a question, which ought not to be hastily decided, how far we should be justified in running even the most remote risk of explosion in establishments such as lighthouses, whose sudden failure might involve consequences of the most fatal description, and whose situation is often such, that their re-establishment must be a work of great expense and time. Gas is, besides, far from being suitable in catoptric lights, to which, in many cases (especially when the frame is moveable, as in revolving lights), it could not be easily applied. The oil most generally employed in the Lighthouses of England is the sperm oil of commerce, which is obtained from the South Sea whale (Physeter macrocephalus). In France, the colza oil, which is expressed from the seed of a species of wild cabbage (Brassica oleracea colza), and the olive oil are chiefly used; and a species of the former has lately been successfully introduced into the Lighthouses of Great Britain. Of all these oils, the purified sperm oil has hitherto been generally considered the most advantageous for lighthouse purposes; but there is every reason for anticipating that the late adoption of the colza oil in many of the British Lights, on the suggestion of Mr Joseph Hume, M.P., while chairman of a select committee of the House of Commons on Lighthouses, will lead to an important saving, as its combustion produces an equal quantity of light at somewhat more than one-half of the expense for spermaceti oil. Careful trials have been made of this oil; and on the 10th of March 1847, I was enabled to report the results to the Commissioners of Northern Lighthouses in the following terms:
“1. The colza oil possesses the advantage of remaining fluid at temperatures which thicken the spermaceti oil so that it requires the application of the frost lamp.
[198]
“2. It appears, from pretty careful photometrical measurements of various kinds, that the light derived from the colza oil is, in point of intensity, a little superior to that derived from the spermaceti oil, being in the ratio of 1·056 to 1.
“3. The colza oil burns both in the Fresnel lamp and the single Argand burner with a thick wick during seventeen hours without requiring any coaling of the wick or any adjustment of the damper; and the flame seems to be more steady and free from flickering than that from spermaceti oil.
“4. There seems (most probably owing to the greater steadiness of the flame) to be less breakage of glass chimneys with the colza than with the spermaceti oil.
“5. The consumption of oil, in so far as that can be ascertained during so short a period of trial, seems in the Fresnel lamp to be 121 for colza, and 114 for spermaceti; while in the common Argand, the consumption appears to be 910 for colza, and 902 for spermaceti.
“6. If we assume the means of these numbers, 515 for colza, and 508 for spermaceti, as representing the relative expenditure of these oils, and if the price of colza be 3s. 9d., while that of spermaceti is 6s. 9d. per imperial gallon, we shall have a saving in the ratio of 1 to 1·755, which, at the present rate of supply for the Northern Lights, would give a saving of about L.3266 per annum.
“Of these conclusions, the three last may be considered as more or less conjectural, being founded on data derived from too short a trial; but the striking agreement of the results obtained at the six lights in which the experiments were made, tends in some measure to supply the place of a longer period of trial; and I have no hesitation, therefore, in recommending the Board at once to introduce the use of the colza oil into all the dioptric lights, except that of Skerryvore, where some special reasons induce me to defer the change for another season. In the catoptric lights, the only reason for not making an equally extensive trial is the necessity for renewing all the burners, which require to be so constructed as[199] to receive thick wicks of brown cotton; and it may perhaps be considered prudent to proceed with some caution in changing the apparatus, so as to suit it for burning a patent oil, the circumstances attending the regular and extensive supply of which are not yet fully known. I may remark, that I have burnt the colza oil in the solar lamp alluded to in my last report; but I disapprove of it as tending to elongate the flame vertically, and thus to decrease its horizontal volume. The elongated form of flame increases the divergence vertically where the light is lost, and so far circumscribes its horizontal range where it is most required. I have therefore substituted the thick wick burner for the solar lamp, whereby an equally complete combustion is obtained, and the proper form of the flame is at the same time preserved.”[36]
[36] Since the above report was written, the price of colza oil has risen; and other circumstances have occurred to justify the caution as to the universal adoption of that oil.
Drummond and Voltaic Lights. The application of the Drummond and Voltaic lights[37] to lighthouse purposes is, owing to their prodigious intensity, a very desirable consummation; but it is surrounded by so many practical difficulties that, in the present state of our knowledge, it may safely be pronounced unattainable. The uncertainty which attends the exhibition of both these lights, is of itself a sufficient reason for coming to this conclusion. But other reasons unhappily are not wanting. The smallness of the flame renders them wholly[200] inapplicable to dioptric instruments, which require a great body of flame in order to produce a degree of divergence sufficient to render the duration of the flash in revolving lights long enough to answer the purpose of the mariner. M. Fresnel made some experiments on the application of the Drummond light to dioptric instruments, which completely demonstrate their unfitness for this combination. He found that the light obtained by placing it in the focus of a great annular lens was much more intense than that produced by the great lamp and lens; but the divergence did not exceed 30′; so that, in a revolution like that of the Corduan Light, the flashes would last only 1¹⁄₃ second, and would not, therefore, be seen in such a manner as to suit the practical purposes of a revolving light. The great cylindric refractor used in fixed lights of the first order, was also tried with the Drummond light in its focus; but it gave coloured spectra at the top and bottom, and only a small bar of white light was transmitted from the centre of the instrument. The same deficiency of divergence completely unfits the combination of the Drummond light with the reflector for the purposes of a fixed light, and even if this cause did not operate against its application in revolving lights on the catoptric plan, the supply of the gases, which is attended with almost insurmountable difficulties, would, in any case, render the maintenance of the light precarious and uncertain in the last degree.
[37] The Drummond light is produced by the ignition or combustion of a ball of lime (³⁄₈ inch diameter) in the united flames of hydrogen and oxygen gases, and is equal to about 264 flames of an ordinary Argand Lamp with the best Spermaceti oil. It derives its name from the late Lieut. Drummond, R. E., who first applied it in the focus of a paraboloïd for geodetical purposes, and afterwards proposed it for Lighthouses. (See his Account of the Light in the Phil. Trans. for 1826, p. 324, and for 1830, p. 383.) The Voltaic light is obtained by passing a stream of Voltaic electricity from a powerful battery between two charcoal points, the distance between which requires great nicety of adjustment, and is the chief circumstance which influences the stability and the permanency of the light. The Voltaic light greatly exceeds the Drummond light in intensity, as ascertained by actual comparison of their effects; but the ratio of their power has not been accurately determined. It was first exhibited in the focus of a reflector by Mr James Gardner, formerly engaged in the Ordnance Survey of Great Britain.
Mr Gurney’s Lamp. In 1835, Mr Gurney proposed the combination of a current of oxygen with the flame of oil, in order to obtain a powerful light of sufficient size to produce the divergence required for the illumination of lighthouses. The Trinity-House of London entertained the proposal, and made some experiments on this important subject; but the plan was finally rejected as disadvantageous in practice.
Argand Burners. Until the invention by Argand (about the year 1784), of the lamp with a double current of air, the art of illumination seems to have received no improvement, and to have occupied very little attention from the time of Cardan, or at all events of Dr Hook,[201] who, about the year 1677, in a monograph entitled “Lampas,” made some important observations on the constitution of flame, so as to make one wonder that he should have stopped short of the discoveries of later inventors. Before Argand’s time, every wick consisted of a solid cord, whose flame was fed only by the current of air on its outside; and the consequence of this arrangement is, that the stream of vapour or smoke, especially from the centre of thick wicks, escapes unburnt, because, before it reaches the height at which the combustion of the central stream can take place, its temperature has become too low to admit of its ignition.[38][202] The chief improvements which had been made, consisted in varying the level of the oil in the cistern, or in attempts to render that level constant, by mechanical means, and in lessening the thickness of the wick, by spreading its substance into a flat form, thus reducing the stream of gas which escapes from the centre of a thick cylindric wick without being burnt, and thereby causing a more complete combustion, and producing less smoke and a whiter flame. To Argand belongs the great merit of having first formed the wick into a hollow cylinder, thus supplying the flame with two currents of air, one of which, as in the case of the solid wick, envelopes the flame, and the other, passing through the centre of the wick, is enveloped by the flame itself. He also added a chimney, which served to defend the flame from irregular draughts of air, and to regulate the proportion between the velocities of the currents of air and the stream of gas. This was indeed a most important step in the art of illumination, and causes the great difference between the incomplete combustion, which, owing chiefly, as we have seen, to a defect in the supply of air, always takes place with a solid wick (from which much unburnt gas escapes in the form of smoke), and that more perfect combustion in which passage is given for a free current of air through the centre of the wick. The invention of Argand came nearly perfect from his hands; and but a few slight modifications of his original arrangement have been introduced. The Argand burner consists of two concentric tubes or cylinders, separated by a small annular space, which is shut at the bottom, and communicates by a pipe with the oil fountain, whose level ought to be a little below the level of the upper edge of the cylinders. In this annular space, partly filled with oil from the fountain, stands a cylindric wick of cotton, loosely wove, into which the oil rises freely by capillary action.[203] The wick has its lower edge fixed to a metallic ferule or ring, called a wickholder, which (by means of a peculiar arrangement, to be afterwards described) gives the power of raising or depressing the wick to any convenient level with regard to the burner. A cylinder of glass, of greater diameter than the burner, rests on a gallery or ring which hangs from the burner and surrounds it. This glass cylinder, or chimney as it is generally called, should stand vertically with its axis coincident with that of the burner itself. The effect of this arrangement is obvious, and has already in part been indicated. The flame is thus necessarily bounded on all sides by two conical concentric surfaces, one external and concave, and the other internal and convex, both of which receive a free current of air. The flame is therefore very thin in every direction; and, as a consequence of the mutual radiation of its different parts on each other, it is throughout its entire surface of more equal temperature than can ever be attained in the thick solid wick or the narrow flat one. The glass cylinder also increases the force of the two currents which pass outside and inside of the flame; and the union of so many favourable circumstances produces a greater amount of pure light than has yet been obtained by any other method. The contraction of the glass chimney (known by the technical name of the shoulder) at a point a little above the level of the wick, tends to direct the current of air inwards on the flame, thereby causing a more perfect combustion and the evolution of more light.
[38] That the form of a flame is necessarily conoidal, and that its height is determined by the relation subsisting between its diameter and the continually varying velocities of the currents of gas and air, may be easily shewn; and the combustion of each annular film of the stream of gas from the wick can take place only at a level determined by, and continually varying with, the ratio of the velocities of the streams of gas and air. I am unwilling to offer this explanation in my own words, when those of M. Peclet, in his excellent work, Traité de l’Eclairage, are at hand,—“Let us conceive,” says he, “a very thin film or layer of inflammable gas placed horizontally, and which rises into the air parallel to itself, with a uniform motion. We shall suppose that it cannot be burnt, except at its circumference, and that the top and bottom of the film are, by some means, preserved from combustion (they are so preserved in ordinary flames, by the films which precede and follow them). If the circumference is at a high enough temperature it will burn; at each instant the film or layer of air, which has assisted the combustion and also the products of that combustion, being very hot, will rise very rapidly, and will make room for other layers or films of air, which will rise in their turn; and as the diameter of the film of gas is continually diminishing, it is obvious that its combustion will offer the appearance of a series of circles continually growing smaller, and terminating at length in a point. If we trace in thought the series of circles which the combustion has successively developed, we shall form a cone whose length will depend on the ratio of the velocities of the films of gas and of air which escape after combustion. If, for example, the velocity of the current of air were very great, compared to the velocity of the cylinder of gas, the entire combustion would take place, while the film of gas passes over a very small space; and the cone formed by the succession of luminous circles would, consequently, be very short. If, on the contrary, there were but a very small difference between these velocities, the luminous circles would only appear at considerable intervals from each other; for the air which had served for combustion, being unable to feed it longer, the surface of the cylinder could not become luminous until the difference of velocity had freed it from the air which had served for the preceding combustion. If, then, we imagine a set of similar films succeeding each other, each of them would give rise to the same series of coloured rings; and as there would be a film in each section of the cone in a state of combustion at the same instant of time, the cone would, of course, appear luminous throughout its height.”—Peclet, Traité de l’Eclairage, p. 51.
Great as the improvement of Argand undoubtedly was, the value of the lamp alone as a means for the illumination of lighthouses must be regarded as comparatively small. The primary object of a lighthouse is to give early notice to the mariner of his approach to the coast, and it is therefore necessary that the light be of such a kind that it may be seen at a great distance. Every one is practically acquainted with the fact that the rays proceed in all directions from a luminous body in straight lines; and if we could obtain a ball equally luminous in every part of its surface, it would give an equal share of light to every part of[204] the inner surface of a hollow sphere, whose centre coincided with the centre of the ball. Again, if an opaque body were placed between the luminous ball and the hollow sphere, the part opposite that body would be deprived of the light by the interception of the rays, and no light would emerge from a hole bored in that part of the surface of the hollow sphere. The bearing of these facts is obvious; and no one can fail to perceive that in the case of a lighthouse illuminated by a single unassisted burner, a seaman could only receive the benefit of that small portion of light which emerges from the lamp in a line joining his eye and the centre of the flame. The other rays would be occupied partly in making the light visible in other parts of the horizon, and but a very small portion of them would be usefully employed for that purpose, while all the rest would be lost by escaping upwards into the sky, or downwards below the plane in which seamen can see a lighthouse. This state of matters would be little improved by increasing the number of burners, as the effective part of the light would only be augmented by the addition of an equally trifling portion of light from each burner. The small pencils of rays thus meeting at the eye of a distant observer, would form a very minute fraction of the whole quantity of light uselessly escaping above and below the horizon, and also at the back of each flame; and the wasteful expenditure of light would be enormous. By such a method no practically efficient sea-light could ever be obtained.
[39] From the Greek κατοπτρον, a mirror; a compound of κατα, opposite to, and ὂπτομαι, I see.
For those defects a simple remedy is found in the well known power possessed by most bodies, of reflecting or throwing back from them the light which falls upon them. This property is not possessed by all reflecting bodies in an equal degree, some absorbing more and some less of the incident light. Perhaps the earliest[205] attempts to apply this property as a corrective for the direction of the rays from a Lighthouse, would be confined to placing plane mirrors behind each lamp; yet this would prove but a partial remedy, as it would still leave the greater part of the light to stray above and below the proper direction. Hollow mirrors of a spherical form might next be tried; and if properly placed with reference to the flame, would constitute a very great improvement in lighthouse illumination. But those steps in the march of improvement are more imaginary than real; and I am not aware of any well authenticated records of such gradual attempts having preceded the adoption of the right mode of applying reflection as a means of rectifying the direction of the rays emerging from a lighthouse. There is, on the contrary, distinct evidence that the impulse given by Argand’s invention, led to an immediate adoption of the most perfect form of reflecting instruments.
Application of Paraboloïdal Mirrors into Lighthouses. The name of the inventor of paraboloïdal mirrors and the date of their first application to Lighthouses, have not been accurately ascertained. The earliest notice which I have been able to find, is that by Mr William Hutchinson, the pious and intelligent author of a quarto volume on “Practical Seamanship” (published at Liverpool in 1791), who notices (at p. 93) the erection of the four lights at Bidstone and Hoylake, in the year 1763, and describes large parabolic moulds, fashioned of wood and lined with mirror-glass, and smaller ones of polished tin-plate, as in use in those Lighthouses. Mr Hutchinson seems to have understood the nature, properties, and defects of the instruments which he describes, and has shewn a good acquaintance with many of the most important circumstances to be attended to in the illumination of Lighthouses. Many claims to inventions rest on more slender grounds than might be found in Mr Hutchinson’s book for concluding him to have first invented the paraboloïdal mirror and applied it to use in a Lighthouse;[40] but, in the absence of any statement as to the date when[206] the mirrors were really adopted, the merit of the improvement must, in justice, be awarded to others.
[40] Mr Hutchinson seems also (“Practical Seamanship,” p. 198) to have tried speculum metal as a material for Lighthouse reflectors.
M. Teulere, a member of the Royal Corps of Engineers of Bridges and Roads in France, is, by some, considered the first who hinted at the advantages of paraboloïdal reflectors; and he is said, in a memoir dated the 26th June 1783, to have proposed their combination with Argand lamps, ranged on a revolving frame, for the Corduan Lighthouse. Whatever foundation there may be for the claim of M. Teulere, certain it is that this plan was actually carried into effect at Corduan, under the directions of the Chevalier Borda; and to him is generally awarded the merit of having conceived the idea of applying paraboloïdal mirrors to lighthouses. These were most important steps in the improvement of lighthouses, as not only the power of the lights was thus greatly increased, but the introduction of a revolving frame proved a valuable source of differences in the appearance of lights, and, in this way, has since been the means of greatly extending their utility. The exact date of the change on the light of the Corduan is not known; but as it was made by Lenoir, the same young artist to whom Borda, about the year 1780, entrusted the construction of his reflecting circle, it has been conjectured by some that the improvement of the light was made about the same time. The reflectors were formed of sheet-copper, plated with silver, and had a double ordinate of 31 French inches. It was not long before these improvements were adopted in England, by the Trinity-House of London, who sent a deputation to France to inquire into their nature. In Scotland, one of the first acts of the Northern Lights Board in 1786, was to substitute reflectors in the room of the coal-light then in use at the Isle of May in the Frith of Forth, which, along with the light on the Cumbrae Isle in the Frith of Clyde, had, till that period, been the only beacons on the Scotch coast. The first reflectors employed in Scotland were formed of facets of mirror glass, placed in hollow paraboloïdal moulds of plaster, according to the designs of the late Mr Thomas Smith, the Engineer of the Board,[207] who (as appears from the article Reflector, in the Supplement to the third edition of the Encyclopædia Britannica) was not aware of what had been done in France, and had himself conceived the idea of this combination. The same system was also adopted in Ireland; and in time, variously modified, it became general wherever lighthouses are known.
To enable us to enter on the subject of the proper forms of reflectors, we must glance very briefly at the Reflection. laws of reflection. Those laws are two in number. 1st, The ray which falls on a reflecting surface, called the incident ray, and the ray which leaves the reflector, called the reflected ray, are always in one plane, which plane is perpendicular to the reflecting surface. 2d, The angle which the reflected ray makes with the reflector is always equal to the angle which the incident ray makes with it, or, in other words, the angle of incidence is equal to the angle of reflection.[41]
[41] This will be more readily understood by referring to the accompanying figure (No. 22), in which CDEF is the reflecting surface; GHOKI the plane of reflection perpendicular to that surface; BO a line perpendicular or normal to the surface CDEF; and AO the incident ray. Then if in the plane GHOKI, the angle BOI be made equal to AOB, OA′ is the reflected ray; BOG is then the angle of incidence; and BOI the angle of reflection. GOH and IOK, which are the complements of those angles, are, indeed, more strictly speaking, the angles of incidence and reflection; but in cases where the reflecting surface is curved, it is more convenient to refer the angles to the normal BO.
Fig. 22.
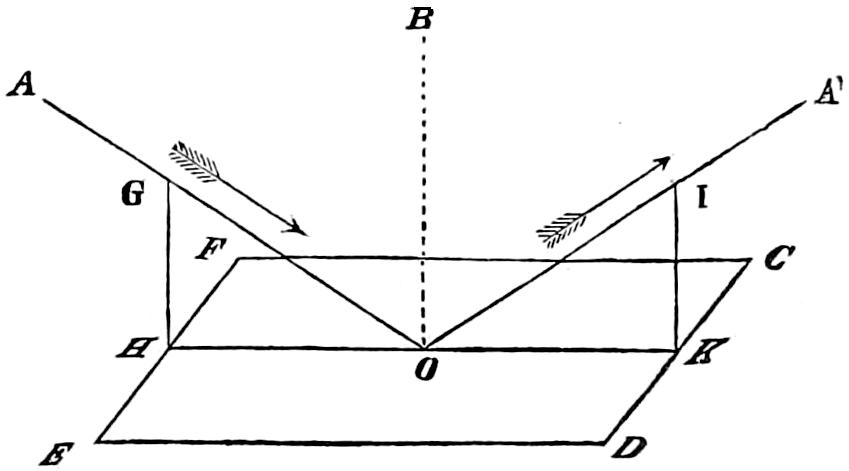
It would lead to prolixity altogether superfluous in this place, to explain, in a rigorous manner, the effects produced by various reflecting surfaces on the direction of the rays incident on them; as any one who comprehends the laws of reflection just enumerated, may easily satisfy himself of the following truths: 1st, That a plane mirror makes no change on the divergence of the rays, but merely causes them to emerge from its surface in the same direction as if they had come from a point as much behind the mirror[208] as the luminous body lies in front of it. 2d, A convex reflecting surface increases divergence, and disperses the rays in the same manner as if they had come directly from a point behind it, whose distance from the mirror increases with the distance of the luminous body from its surface, and diminishes with the degree of convexity of the mirror. 3d, A concave surface diminishes the divergence of the rays incident upon it from a point between the surface and its centre of curvature; the distance of the point in which the reflected rays converge diminishing as the distance of the radiant point or the concavity of the mirror is increased. It is obvious, therefore, that concave mirrors are those which are required to produce a correction of the path of the rays, so as to apply them to most advantage in a lighthouse, the object to be attained being that of throwing the greatest amount of light towards given points in the horizon, and collecting the divergent rays, which, as we have already seen, are scattered above and below it.
To simplify our view of this matter, I shall, in the first place, suppose that the object to be attained is to throw the whole rays of a single lamp, with an infinitely small flame, to a given mathematical point at a moderate distance; and, as this is a case which can hardly occur in the practice of Lighthouse illumination, I content myself with observing that this object may be attained approximately by placing the lamp in front of a spherical mirror at any distance greater than half the radius of the curve surface, or accurately by placing it in one focus of an elliptical mirror; in all those cases the rays would meet in the opposite, or, as they are termed, conjugate foci. Let us next suppose that our object is to illuminate, by means of a mathematical point of light, a small circular space on the horizon equal in diameter to the mirror employed; this object will be rigorously attained only by placing the light in the focus of a paraboloïdal reflector. The same object may be approximately attained by placing the light in a spherical mirror, at a point half-way between the centre of curvature and the surface of the mirror, provided the surface of the mirror shall[209] subtend only a small angle at the centre of curvature. The paraboloïdal mirror, on the contrary, has the property of converging to the focus parallel rays falling upon every point of its surface, however extended it may be.
Paraboloïdal Mirrors. Any one practically acquainted with this subject, must at once perceive that the paraboloïdal mirror completely fulfils one great object required in a lighthouse; and to render this more obvious to the general reader, I shall, for the present, confine my remarks to the case of those lighthouses which exhibit to the mariner in every part of the horizon, pencils of light at certain intervals of time, separated by periods of darkness, reserving the consideration of Lights which are continually in sight all round the horizon or over a given portion of it, for a subsequent part of these Notes. In doing this, I am aware that I may appear to be departing from the strict order of investigation, by suddenly introducing the idea of motion; but a little consideration will, I think, satisfy the reader that this is, in reality, the more convenient mode of treating the subject. Let us suppose, then, that our object is to give occasional flashes of light, separated by intervals of darkness, to seamen in various azimuths and at various distances from a lighthouse. It is obvious that this may be most efficiently done by causing concave mirrors, which collect the rays from lamps placed in them and thereby increase the light in front of the mirror, to revolve round a vertical axis with a velocity suited to produce the required number of flashes in a given time. The paraboloïdal mirror is best adapted for producing this effect, for the following reasons: 1st, Because it alone produces a rigorous parallelism of all rays proceeding from its focus, and falling upon any point of its surface, however distant the point of reflection from that focus, or however far in front of it. 2d, Because it therefore embraces in its action the greatest number of the whole rays coming from the focus, and, cæteris paribus, will produce the strongest light. 3d, Because the theoretical object to be attained is to make those flashes equally powerful at any distance, an effect which would[210] be rigorously fulfilled by placing an infinitely small flame in a perfect paraboloïdal mirror. And, 4th, Because, although absolute equality of luminousness at any distance is not attainable, and, in practice, is inconsistent with other conditions required in a useful light, we still, by using the parabolic mirror, make the nearest approach to parallelism of the reflected rays, and consequently obtain the strongest light which is consistent with a due regard to a certain duration of the flash on the eye of a distant observer, which is measured by the angle of the luminous cone projected to the horizon.
Having thus so far anticipated what some might think would more naturally have occurred in a subsequent part of these Notes, I return to a more detailed consideration of the parabola itself, and its product, the paraboloïdal mirror. I content myself, however, with describing the parabola, by that property which peculiarly adapts it to the purposes of a lighthouse. The parabola, then, is a curve of the second order, obtained by cutting a cone in a plane parallel to one side, which possesses this remarkable property, that a line drawn from the focus to any point in the curve, makes, with a tangent at that point, an angle equal to that which a line parallel to the axis of the curve makes with that tangent.[42]
[42] See third corollary to Proposition III. of Wallace’s Conic Sections, which shews that a tangent to the parabola makes equal angles with the diameter which passes through the point of contact and a straight line drawn from that point to the focus. The curve may be traced in two different ways, both dependent on the property, that the distance of any point in the parabola from the focus is equal to its distance from the directrix.
To draw the curve mechanically (fig. 23), let F be the focus, MF the focal distance (chosen at pleasure according to rules which I shall afterwards notice), KMX is the axis, and AB the directrix (the dotted line f F e, bounded by the curve at either end, would then be the parameter or latus rectum). Place the edge of the straight ruler AKHB along the directrix; and let LHB be a square ruler which may slide along the fixed ruler AKHB, so that the edge HL may be constantly perpendicular to AB, or parallel to MX, the axis; let LDF be a string equal in length to HL, and having one end fixed in F, and the other at L, a point in the sliding square. Then if the string be stretched by a pencil D, so as to keep the part DL close to the edge of the square, and if at the same time the square be gently pushed along the line AB, the point D will be forced to move along the edge LH of the square, and will trace out a curve which will be the required parabola. This is obvious from the consideration, that the string LDF being equal in length to LH, and LD being common to both, the remainder DF must be equal to the remainder DH, so that the point which traces the curve being equidistant from the directrix and the focus must, in terms of the above definition, describe a parabola.
Fig. 23.
In the second place, the same property, as already stated, furnishes us with the means of tracing the curve by finding successive points therein. Draw a line a b perpendicular to the axis OX, and the position in this line, of a point p through which the curve passes, is easily found thus: Describe from F the focus as a centre with a radius equal to the perpendicular distance O d of the line a b from the directrix AB, a circle cutting the line a b in two points p and p′; then both these points are in the curve. By repeating the same process, any number of points in the curve may be obtained.
Fig. 24.
Lastly, from the equation to the curve, the length y of any ordinate may be computed, in terms of m its principal focal distance, and x its abscissa, by the simple expression,—
y = √4 m x.
It is easy to see, that if this curve revolve about its axis, it will generate a parabolic conoid, which we may conceive to be concave or convex, as we please. If the surface be concave, we obtain the mirror of which we are in search; for every principal section, or that passing through the axis of such a mirror, will necessarily[211] possess the same properties as that of the plane curve, and will each have a focus meeting in one and the same point; the union of all these sections will therefore form a mirror capable of reflecting, in a direction parallel to the axis and to each other, all the rays of light which fall on its surface.
[212]
We have already seen that a perfect paraboloïdal mirror, with a point of light infinitely small placed in the focus, would project a beam equally intense at any distance, every transverse section of which would be of the same superficial extent. Divergence of Paraboloïdal Mirrors. In practice, these conditions can never be rigorously fulfilled. No perfect instrument can come from the hands of man, and every mirror must of necessity possess many defects. To obtain a true mathematical point of light is also impossible; and for the purposes of a lighthouse, it would be completely useless, as will appear from the following simple considerations. Let us suppose that a true paraboloïdal mirror, having a double ordinate or space of two feet, and illuminated by a point of light, projects a truly cylindric beam of light to the horizon, and that it revolves horizontally round a vertical axis, with such a velocity as to cause the beam to pass over the eye of an observer stationed at the distance of 100 feet in one second of time, and we shall find that another observer, at a distance of 15 miles from the mirror, would not see the light at all, although of equal size, because its velocity at that distance would be so great as only to be present to his eye for ¹⁄₇₉₂d of a second, a space of time far too short to make a perceptible impression on the eye of a distant observer. This is no mere hypothesis unsupported by facts; for I shall have occasion, in another part of these Notes, to describe certain experiments, by which it was ascertained that a beam of light emerging from a lens, and passing over the eye of an observer at 14 miles distance, in a space of time equal to ¹⁄₁₆₆th of a second, became altogether invisible at that distance.
For this evil, happily a very simple and efficient remedy may be found in what may be said to constitute a theoretical defect in the combination of the Argand burner with the reflector. The burner, instead of being a mathematical point, has generally a diameter of about one inch, and a ray proceeding from the edge of the flame to any point on the surface of the mirror, makes with the line joining that point and the principal focus an angle which,[213] being repeated by reflection, gives the effective divergence of each side of the mirror at that point.[43]
[43] This is easily understood by reference to the accompanying figure (No. 25.), in which AOB is a central section of a paraboloïdal mirror.
Fig. 25.
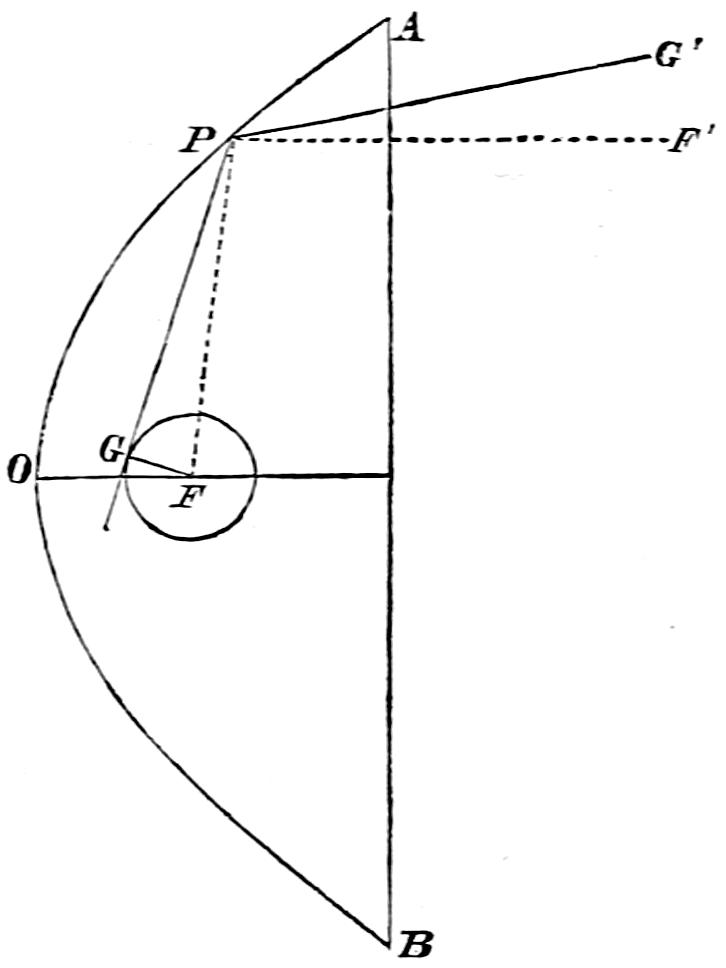
PF = distance from the focus F to a point in the curve P, and PG a tangent drawn from P to the surface of the flame at G;
FG = radius of the wick or flame;
and GPF = G′PF′ = divergence of one side of mirror, and consequently 2 GPF = the whole effective divergence of the mirror at that cross section.
Now sin GPF = GFPF or the sine of the divergence from each point = Radius of flame.Distance from focus to point of reflection.
Fig. 26.
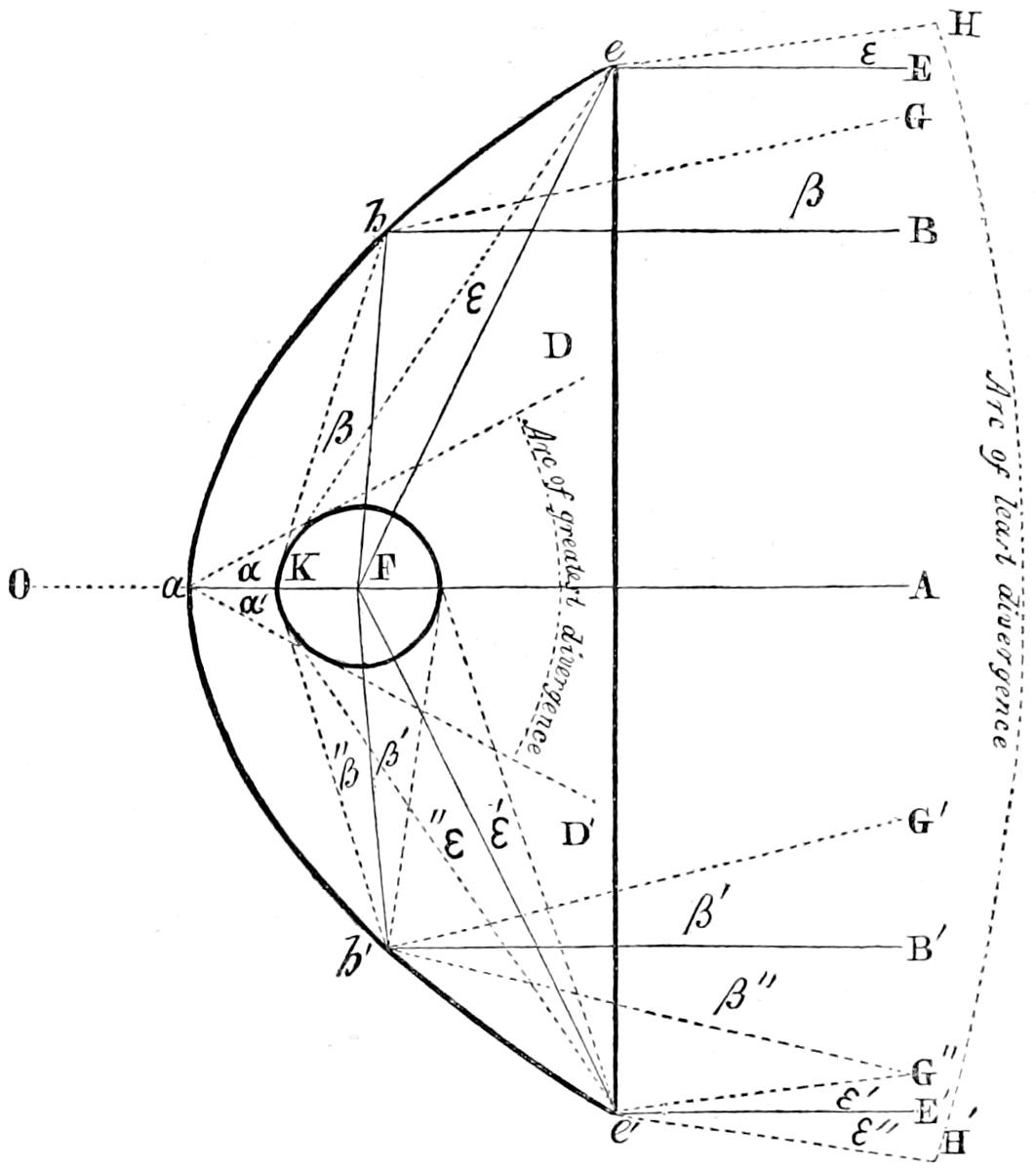
It is obvious that this quantity which varies inversely with the distance of the reflecting surface from the focus, is greatest at the vertex of the curve, and least at the sides or edges of the paraboloïd. The most useful part of the light, or that which conduces to the strongest part of the flash in a revolving light, is that which is derived from the cone of rays which is bounded by the limits of this minimum divergence; for the faint light which first reaches the eye of a distant observer, in the revolution of a reflector, is not that which is reflected by the sides or edges, as might at first be supposed, but proceeds from the centre. The light, in fact, gradually increases in power in proportion as additional rays of reflected light are brought to bear on the observer’s eye, until, last of all, the extreme edge of the mirror adds its effect. The light continues in its best state until the opposite limit of minimum divergence has been reached, when it begins gradually to decline, receding from the margin of the mirror towards the centre, and, having at length reached the limit of its maximum divergence, it finally disappears at the centre. The increase and decline of the power of a mirror in the course of its movement round the circle of the lantern, as seen by a distant observer, will, therefore, in all its different states, be measured by the areas of a series of circles described from its focus, with radii equal to the distance of the focus from the point of the mirror which reflects to the observer’s eye the extreme ray which can reach him in any given position of the mirror. This will be more easily understood by referring to the accompanying diagram, Fig. 26, in which e a e′ is the principal section of a paraboloïdal mirror, F its focus, αFA its axis, and FK the radius of the flame. If the reflector revolve round a vertical axis at O, an observer placed in front of it (at a distance so great that the subtense of the mirror’s width would be small enough to allow us safely to consider the lines drawn from e and e′ to his eye as parallel), would receive the first ray of light in the direction a D, as reflected at a, from a single point on the edge of the flame (where a tangent to the flame would pass through a); and conversely he would lose the last ray at D′, as reflected at a, from a single point on the opposite margin of the flame; and hence, as above, the greatest divergence is measured by the angle which the flame subtends at the vertex a of the mirror, being the sum of the angles α and α′. We shall next suppose the mirror to move a little, so that the observer may receive at G a ray of light from some other point in the flame which is reflected at b; while another ray from an opposite point reflected at b′ would be seen in the parallel direction b′ G′, thus indicating the boundary of a circular portion of the mirror b a b′, the whole of which would reflect light to the distant observer’s eye. Again, let us suppose a ray to come from another part of the flame, and be reflected at the mirror’s edge e into the direction e H, and another from the opposite side of the flame to be reflected at its opposite edge e′, into the direction e′ G″, and we obtain the full effect of the whole reflecting surface, which will continue unabated until the mirror in the course of its revolution shall reflect at e′ to the observer’s eye, a ray from a point in the margin of the flame (through which a tangent drawn from e′ to the flame would pass) in such a direction, that the angle which it makes with the axis of the mirror is equal to that subtended by the radius of the flame at the distance F e or F e′. After this the light would recede from the edges of the mirror in the same gradual manner, until it should vanish in the direction a D′, which is the opposite limit of the extreme divergence of the instrument. In the above explanation, I have confined myself simply to the effects of the outer ring of the flame, which is the source of divergence; but I need not remind the reader that every portion of the flame radiates light, which, being reflected, conduces to the effect. Some rays also are passing from the opposite sides of the flame through the true focus, so as to be normally reflected in lines parallel to its axis. The solid lines in the diagram shew the theoretical reflection of rays proceeding from F to b, b′, e, e′, where they are diverted into the directions b B, b′ B′, e E, and e′ E′; and by contrast with the dotted lines, serve to render more perceptible the path of the divergent rays which come from the edge of the flame. The Greek letters indicate the angles of divergence, and point out their relations to each other on either side of the mirror. The arcs of greatest and least divergence are marked in the diagram. This subject will be found treated less directly, but, certainly, more concisely and neatly, by Mr W. H. Barlow, in a paper on the Illumination of Lighthouses in the London Transactions for 1837, p. 218.
It is still more obvious that a perfect paraboloïdal figure, and a luminous point mathematically true, would render the illumination of the whole horizon by means of a fixed light impossible; and it is only from the divergence caused by the size of the flame which is substituted for the point, that we are enabled to render even revolving lights practically useful. But for this aberration, the slowest revolution in a revolving light would be inconsistent with a continued observable series, such as the practical seamen could follow, and would, as we have seen, render the flashes of a revolving light too transient for any useful purpose; whilst fixed lights, being visible in the azimuths only in which the mirrors are placed, would, over the greater part of the distant horizon, be altogether invisible. The size of the flame, therefore, which is placed in the focus of a paraboloïdal mirror, when taken in connexion with the form of the mirror itself, leads to those important modifications in the paths of the rays and the form of the resultant beam of light, which have rendered the catoptric system of lights so great a benefit to the benighted seamen.
In order to obtain a mirror capable of producing a given divergence of the reflected beam, therefore, we must proportion its focal distance to the diameter of the flame in such a manner, that the sine of one-half of the whole effective divergence of the mirror, may be equal to the quotient of the radius of the flame, divided by the distance of a given point on the surface of the mirror from the focus. The best proportions for paraboloïdal mirrors depend on the objects which they are meant to attain. Those which are intended to give great divergence to the resultant beams, as in fixed lights, capable of illuminating the whole horizon at one time, should[216] have a short focal distance; while those mirrors which are designed to produce a nearer approach to parallelism (as in the case of revolving lights which illuminate but a few degrees of the horizon at any one instant of time), will have the opposite form. Those two objects may, no doubt, be attained with the same mirror, by increasing or diminishing the size of the burner; but that is by no means desirable, as any change on the size of a burner, which is found to be the best in other respects, must be considered as to some extent disadvantageous.
What I have stated above as to the use of mirrors with a short focal distance for lights of great divergence, proceeds on the assumption, that the penumbral portion of the light on each side of the strongest beam (which is confined within the limits of the least divergence, due to that portion of the mirror where the focal distance is the greatest) is to be pressed into service in the illumination of the horizon; and it is the chief inconvenience which attends the application of paraboloïdal mirrors to fixed lights, that because it is impracticable to apply a number of mirrors sufficient to light the whole horizon with an equally strong light, spaces occur on either side of each reflector in which the mariner has a light sensibly inferior to that which illuminates the sector near the axis of each mirror. This will be best explained by stating the numerical results of the computations of the divergence of the mirrors used in the Northern Lights for this purpose, both at the vertex and the sides. In a mirror whose focal distance is 4 inches, and its greatest double ordinate 21 inches, illuminated by a flame 1 inch in diameter, we find by computation, that the greatest divergence is 14° 22′, and that the strongest arc of light is only 5° 16′; a difference so great, that while the one may admit of the horizon being imperfectly illuminated by means of 26 reflectors, the superior light which would result from confining the duty of each instrument within the range of its best effect, could only be obtained by the use of 68 reflectors, and the expenditure of a proportionately great quantity of oil, not to speak of the great practical difficulty which[217] would attend the arrangement of so many lamps in a lantern of moderate size. In revolving lights, the mirrors are not, as in fixed lights, inconveniently taxed for horizontal divergence, because each portion of the divergent beam visits successively each point of the horizon. In this view of the merits of fixed and revolving lights, I should be disposed to recommend, in any new organisation of lights with parabolic reflectors, the adoption, in fixed lights, of reflectors with a short focal distance and small span, so as to admit of many being ranged around the frame; while in revolving lights, it would be my aim to approach the largest size of reflector that could be made, so as if possible to illuminate each face of the revolving frame by means of a large lamp in a single mirror, with a great focal distance, thereby diminishing the difference between the divergence of the powerful cone of rays reflected from the more distant parts of the mirror and that of the feebler and more diffuse light from its apex.
Effect of Paraboloïdal mirrors. The maximum luminous effect of the reflectors ordinarily employed in fixed lights, as determined by observation, is generally equal to about 350 times the effect of the unassisted flame which is placed in the focus; while for those employed in revolving lights, which are of larger size, it is valued at 450. This estimate, however, is strictly applicable only at the distances at which the observations have been made, as the proportional value of the reflected beam must necessarily vary with the distance of the observer, agreeably to some law dependent upon the unequal distribution of the light in the illuminous cone which proceeds from it. The effect also varies very much in particular instruments. The ordinary burners used in lighthouses are one inch in diameter, and the focal distance generally adopted is 4 inches, so that the extreme divergence of the mirror in the horizontal plane may be estimated at about 14° 22′; while the divergence of the most luminous cone is 5° 16′ for the small reflectors, and 4° 25′ for the larger size. In arranging reflectors on the frame of a fixed light, however, it is advisable[218] to calculate upon a less amount of effective divergence, for beyond 11° the light is very feeble; but the difficulty of placing many mirrors on one frame, and the great expense of oil required for so many lamps, have generally led to the adoption of the first valuation of the effective divergence.
Power of Paraboloïdal Mirrors. The measure of the illuminating power of a paraboloïdal mirror may be estimated as the quotient of the SURFACE of the circle which cuts it in the plane of its greatest double ordinate, divided by the surface of the largest vertical section of the flame, and diminished by the loss of light in the process of reflection. This estimate will be found near enough for all practical purposes; but it is obviously inaccurate, inasmuch as it overlooks the circumstance of the focal distance of each portion of the mirror being different, and the consequent increase in the length of the various trajectories at each point of the surface as you recede from the axis; and the only correct rule, therefore, is, to find an imaginary focal distance which must be the radius of a spherical segment which shall answer the double condition of having its surface equal to that of the greatest cross section of the mirror, and of including, at the same time, a number of degrees equal to those which are brought under the influence of the reflecting action of the paraboloïd. This subject, however, as I have already hinted, is not of great practical importance; and I shall not therefore dilate on it farther, but content myself with saying, that such a line will be found to be a mean proportional between the greatest and least focal distances of the mirror.[44] The large mirrors used in the Northern Lights have about ¹²⁄₁₇ths of the whole light of the lamp incident on their surface; the rest escapes in the comparatively useless state of naturally radiating light.
[44] This subject is treated in detail in M. Barlow’s Paper already noticed. (London Transactions for 1837, p. 212.)
Manufacture of Reflectors. The reflectors used in the best lighthouses, are made of sheet-copper plated in the proportion of six ounces of silver to sixteen ounces of copper. They are moulded to the paraboloïdal form, by[219] a delicate and laborious process of beating with mallets and hammers of various forms and materials, and are frequently tested during the operation by the application of a mould carefully formed. After being brought to the curve, they are stiffened round the edge by means of a strong bizzle, and a strap of brass which is attached to it for the purpose of preventing any accidental alteration of the figure of the reflector. Polishing powders are then applied, and the instrument receives its last finish. The details of this manufacture are given in the Appendix.
Testing of Mirrors. Two gauges of brass are employed to test the form of the reflector. One is for the back, and is used by the workmen during the process of hammering, and the other is applied to the concave face as a test, while the mirror is receiving its final polish. It is then tested, by trying a burner in the focus, and measuring the intensity of the light at various points of the reflected conical beam. Another test may also be applied successively to various points in the surface, by masking the rest of the mirror; but as it proceeds upon the assumption that the surface of the reflector is perfect, and that we can measure accurately the distance from a radiant coincident with the focus to the point of the mirror to be tried, it is in practice almost useless. For such a trial we must place a screen in the line of the axis of the mirror at some given distance from it, and ascertain whether the image of a very small object placed in the conjugate focus, which is due to the distance of the screen in front of the focus, be reflected to any point considerably distant from the centre of the screen through which the prolongation of the axis of the mirror should pass. We thus obtain a measure of the error of the instrument. For this purpose, we must find the position of the conjugate focus, which corresponds to the distance of the screen. If b be the distance to which the object should be removed outwards from the principal focus of the mirror, d the distance from the focus to the screen, and r the distance from the focus to that point of the mirror which is to be tested,[220] we shall have b = r²d as the distance to which the object must be removed outwards from the true focus on the line of the axis.[45]
[45] The truth of this equation may be easily ascertained as follows (See fig. 27):—Let AP be the mirror, F its principal focus, and PH the line of reflection of the ray FP; then an object at I will be reflected at P to the conjugate focus O, where the screen is supposed to be placed. But by construction, FPI = HPO = POF, and the angle at F being common, the triangle FPI is similar to FPO, and hence FO ∶ PF ∷ PF ∶ FI, and FI = PF²FO; and substituting the letters in the text, we get d ∶ r ∷ r ∶ b, and b = r²d.
Fig. 27.
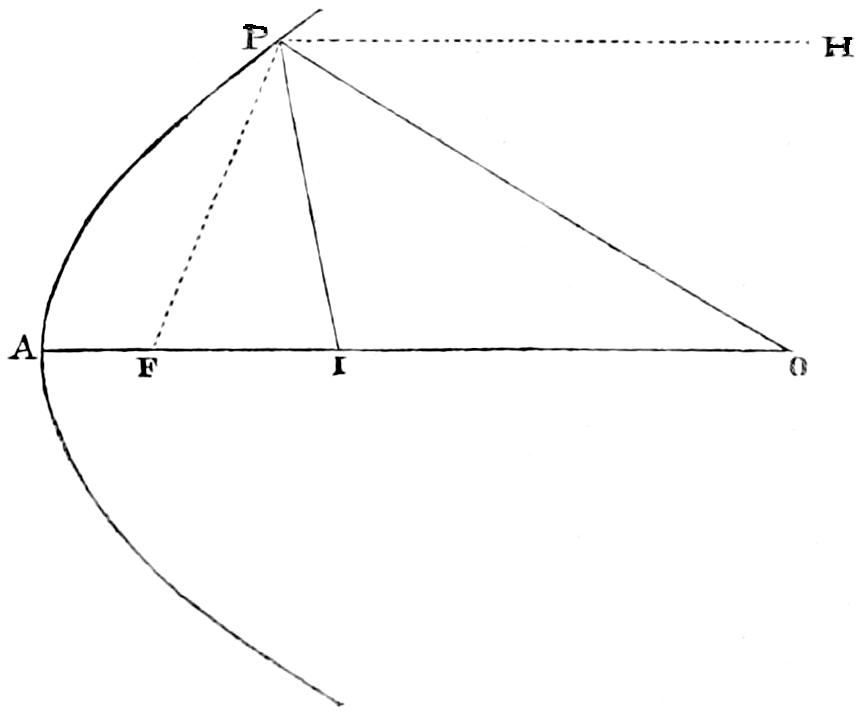
Fig. 28.
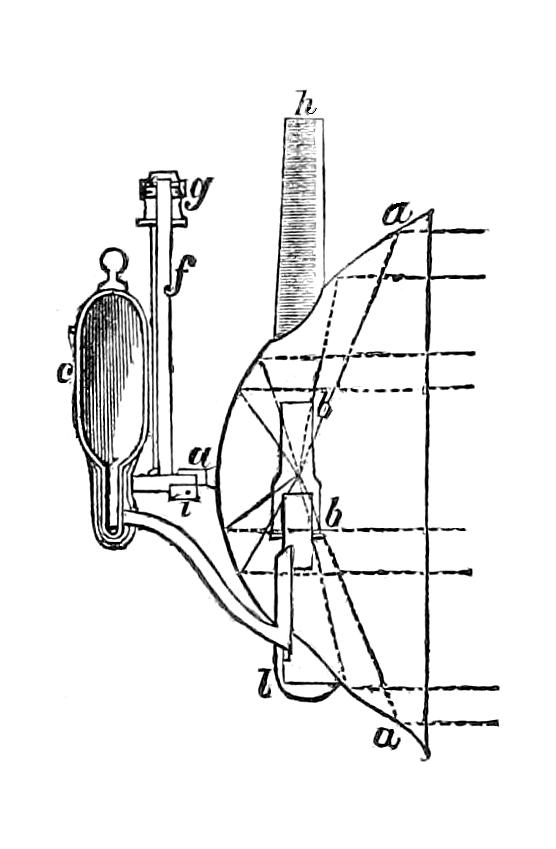
Fig. 29.
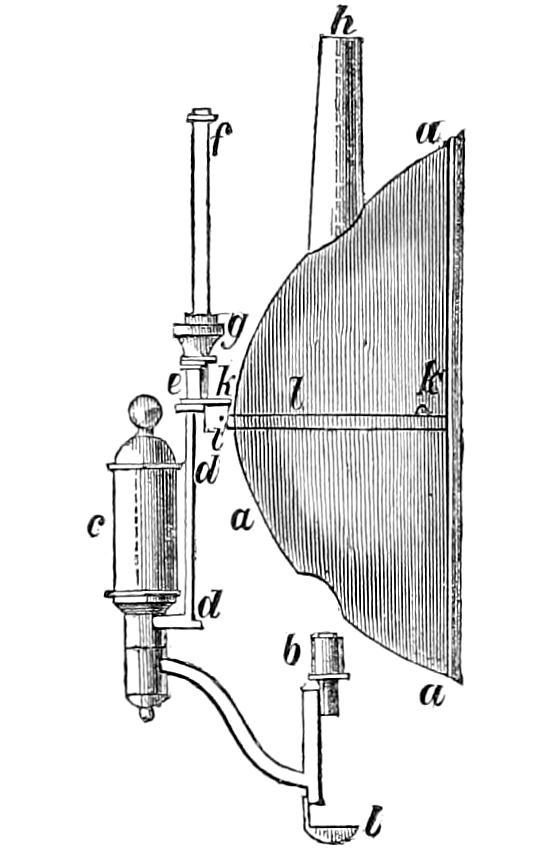
Fig. 30.
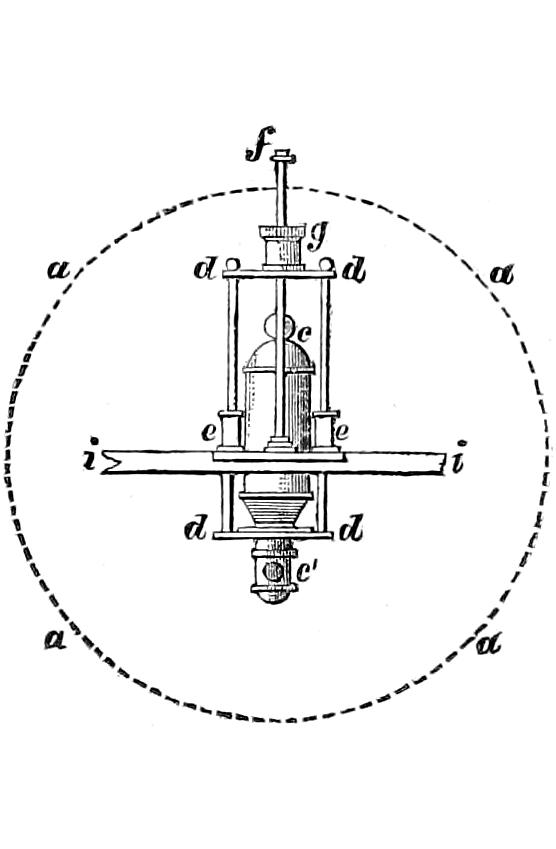
Fig. 31.
Argand Lamps used in Reflectors. The flame generally used in reflectors, is from an Argand fountain-lamp, whose wick is an inch in diameter. Much care is bestowed upon the manufacture of the lamps for the Northern Lighthouses, which sometimes have their burners tipped with silver to prevent wasting by the great heat which is evolved. The burners are also fitted with a sliding apparatus, accurately formed, by which they may be removed from the interior of the mirror at the time of cleaning them, and returned exactly to the same place, and locked by means of a key. This arrangement, which is shewn in figs. 28, 29, and 30, is very important, as it insures the burner always being in the focus, and does not require that the reflector be lifted out of its place every time it is cleaned; so that, when once carefully set and screwed down to the frame, it is never altered. In these figs. a a a represents one of the reflectors, b is the burner, and c a cylindric fountain, which contains 24 ounces of oil. The oil-pipe, the fountain c for supplying oil, and the burner b, are connected with the rectangular frame d, which is moveable in a vertical direction upon the guide-rods e and f, by which it can be[221] let down, so that the burner may be lowered out of the reflector, by simply turning the handle g (as will be more fully understood by examining figs. 28 and 29), which has the effect of forcing a thread (like that of a screw) on the outside of the guide into a groove in the frame, or withdrawing it, and thus allows it to slide down or locks it at pleasure. An aperture of an elliptical form, measuring about two inches by three, is cut in the upper and lower part of the reflector, the lower serving for the free egress and ingress of the burner, and the upper, to which the copper tube h is attached, serving for ventilation; i shews a cross section and a back view of the main bar of the chandelier or frame on which the reflectors are ranged, each being made to rest on knobs of brass, one of which, as seen at k k, is soldered to the brass band l, that clasps the exterior of the reflector. Fig. 28 is a section of the reflector a a, shewing the position of the burner b, with the glass chimney b′, and oil-cup l, which receives any oil that may drop from the lamp. Fig. 30 shews the apparatus for moving the lamp up and down, so as to remove it from the reflector at the time of cleaning it. In the diagram (fig. 30) the fountain c is moved partly down; d d shews the rectangular frame on which the burner is mounted, e e the elongated socket-guides through which the guide-rods slide, and f the guide-rod, connected[222] with the perforated sockets on which the checking-handle g slides. The oil-cup l (covered with a lid and wick-holder, as shewn in fig. 31) also serves as a frost-lamp during the long nights of winter, when the oil is apt to turn thick. It is attached to the lower part of the oil-tube by the arm h; and is lighted about an hour before sunset, so as to prepare the reflector lamp for lighting at the proper time. The communication between the burner and the fountain is easily opened or shut in the burners used in the Scotch Lighthouses, by simply giving the fountain a turn of one quadrant of the horizon round its own vertical axis by means of the round knob at its top, and thereby moving a simple slide-valve, which shuts off the communication between the fountain-tube and lamp-tube. By this mode, the oil is cut off about fifteen minutes before extinguishing the lights, so that when that is done, the burner is quite free of oil.
Fig. 32.
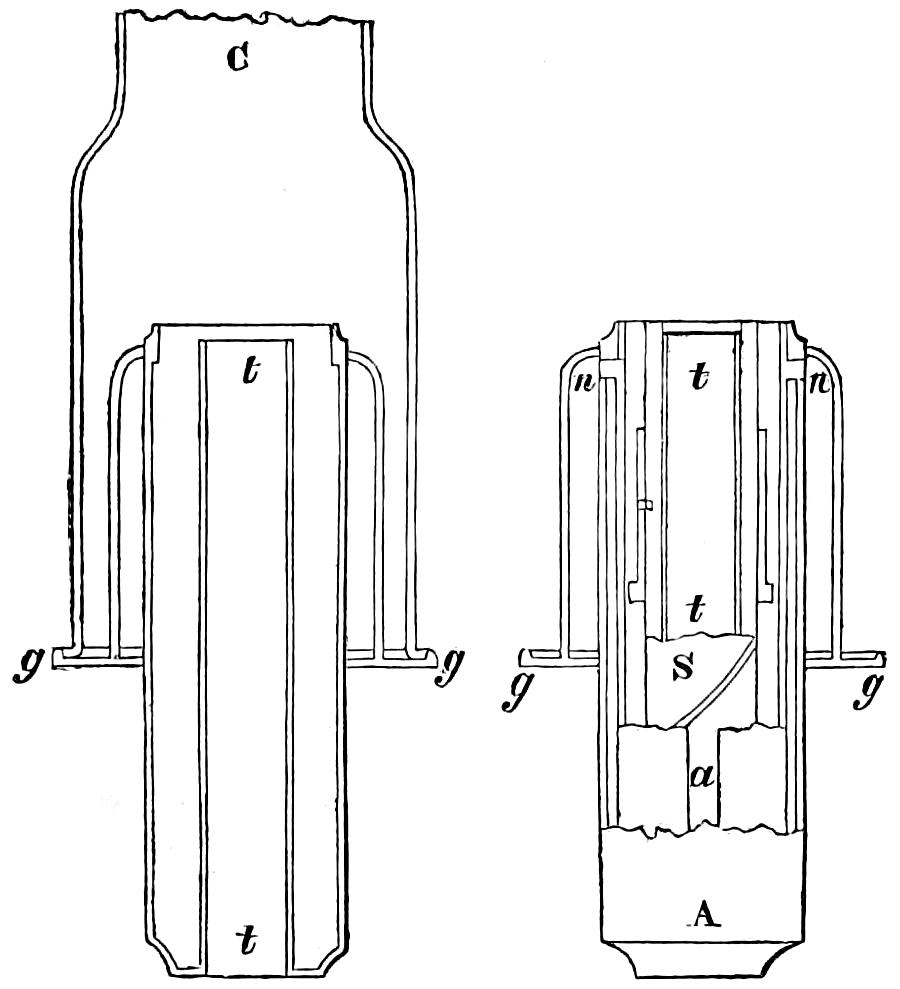
It would needlessly occupy much time and space to describe the various means (many of them sufficiently clumsy) which have been employed, and in many places are still in use, for raising and depressing the wick; it will be enough to say, that they all involve some application of the rack and pinion. Arrangements for Raising or lowering the Argand Wick. I shall, therefore, only describe the method (invented, it is believed, by M. Verzy) which is adopted in all the Lighthouses in the district of the Commissioners of Northern Lights. The arrangement is as follows (see figs. 32, 33, 34, 35, 36):—The inner tube t of the burner is enclosed by a strong tube s, which fits to it tightly, so as not to be easily moved. This strong tube has a spiral groove cut on its outer or convex surface. The wick-holder has two small pegs projecting from it, the one on the inside (not seen), and the other on the outside at a (fig. 33). That on the inside works in the spiral groove of the tube S (figs. 32 and 33), already described as embracing the inner tube t; and all that is required for raising the wick is to make the wick-holder turn round on its vertical axis. This is effected by means of the small external peg a of the wick-holder (fig. 33), which moves in a vertical slit a (figs. 32 and 34), cut in a tube standing[223] in the burner, and concentric with it, and which also moves freely round its axis. Small knobs n n (figs. 32, 34, and 36), at the top of this tube, fit into a notch in the upper ring of the gallery, which supports the glass chimney. By turning this gallery g (see figs. 33 and 36), therefore, motion is given to the tube, with its knobs n n, whose vertical slit a (while it holds the external peg of the wick-holder, and also turns it round along with it) permits that peg a to slide upwards or downwards, and thus the wick-holder rises or falls, according as its own internal peg moves up or down the spiral groove in the tube S. In fig. 32, C shews the glass chimney resting on the gallery g g.
Fig. 33.
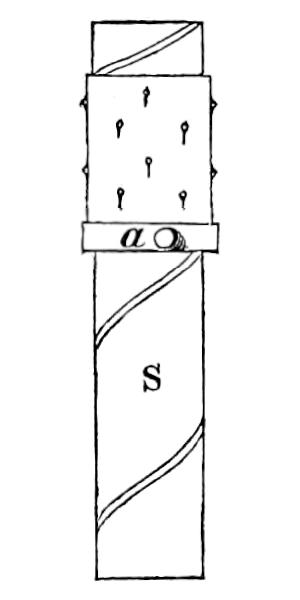
Fig. 34.
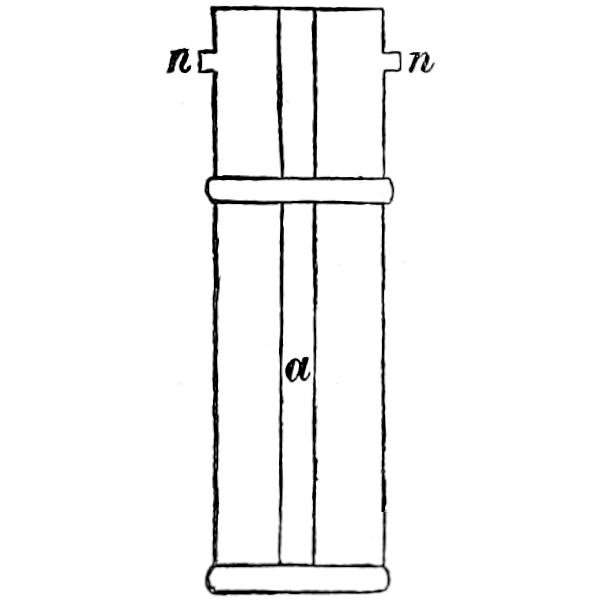
Fig. 35.
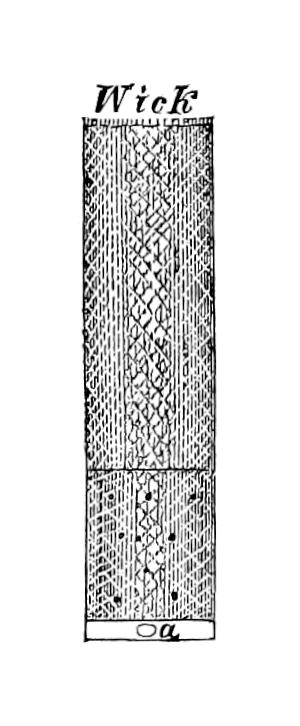
Fig. 36.
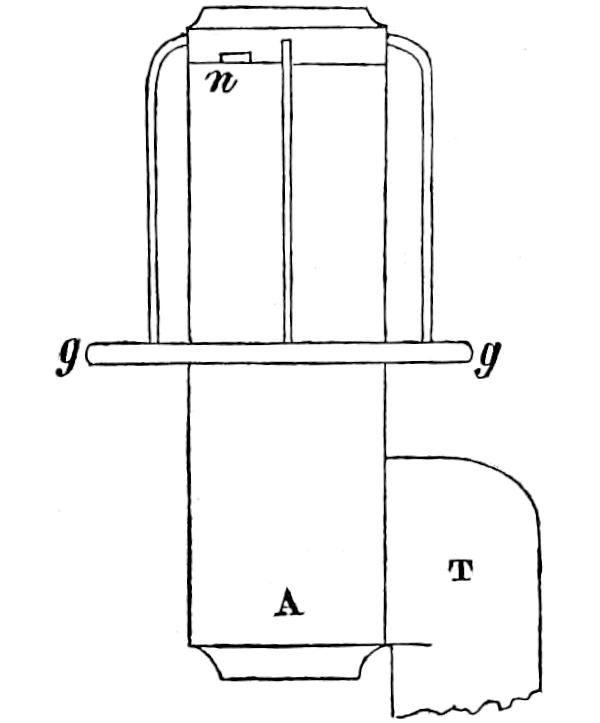
An important point in the economy of the Argand lamp, is the level at which the outlet for the oil, in its passage from the fountain to the burner, should be cut. The cutting of this hole (generally called[224] the flow-hole) in the pipe is termed the Flowing of the Lamp. flowing of the lamp, and is commonly done by successive trials, until the oil stands at the proper level of the burner, before the wick is put in. A more ready and accurate method of accomplishing this object and at once determining the level at which the flow-hole should be cut, was introduced by Mr James Murdoch, the Foreman of Lightroom Repairs to the Scotch Board, and is generally employed in the Northern Lighthouses. Its nature will be readily understood by a reference to the accompanying diagram, No. 37:
Fig. 37.
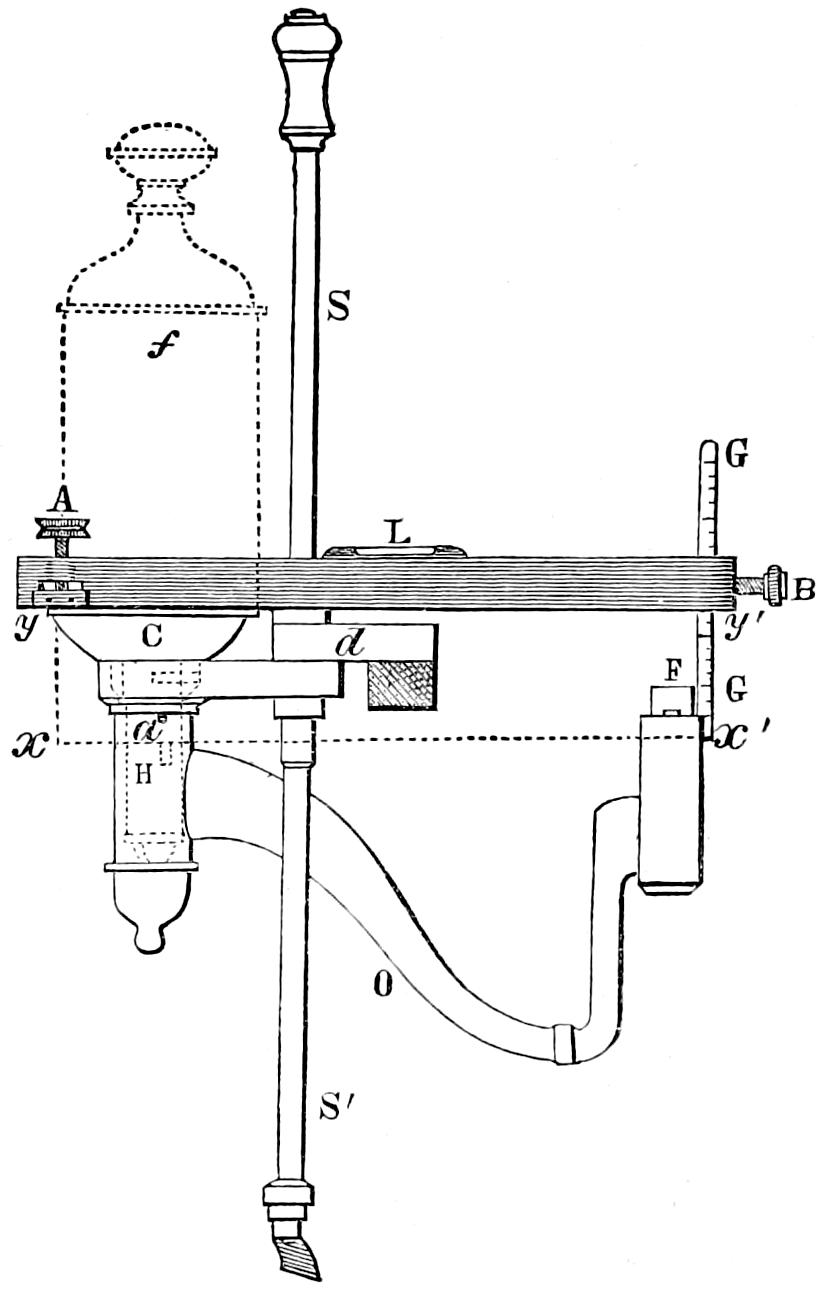
The hatched surface represents a metallic ruler, with a spirit-level at L; C is the cup in which the bottom of the fountain f (shewn in dotted lines) rests. When the fountain is removed, and the ruler rests on the edge of the cup C, the screw at A is used to adjust the level at L; and a gauge GG is allowed to fall until a notch in it at x′ rests on the outer tube of the burner F; the pinching-screw B retains this ruler in its place, and the point x′ indicates the level at which the oil should stand in the burner. The level line x′ x indicates the level on which the top of the flow-hole H should be cut in the fountain-tube, which is shewn in dotted lines within the outer tube, or body of the lamp. In other words, y′ x′ measures the level at which the oil should stand in the burner below the lower edge of the metallic ruler, while the corresponding line y x, at the opposite end, shews the level of the top of the flow-hole H, below the edge of the cup C. The gauge GG applied to that point of the fountain which coincides with the edge of the cup (so that y′[225] coincides with y) measures the length yx = y′ x′; and a set-square applied at x gives the position of H on the fountain-tube. The round dot at a shews the position of the air-hole in the body of the lamp, which establishes a connection between the external air and the surface of the oil. The rods SS′ shew the sliding gear (described as d and f, page 221), and are only introduced to identify this diagram with those of the fountain and burner which have preceded it.
The most advantageous level of the flow-hole depends on many circumstances too obscure and complicated to admit of any systematic elucidation; and it is enough for all practical purposes, to know that the capillary powers of the wick, and the greater or less viscidity of the oil, are the chief circumstances which determine that level. Actual experience is the only sure guide to the best practice in this respect; and I therefore content myself with stating, that it is generally found that the sperm oil should stand in the empty burner at about ³⁄₈ inch below its top. For colza oil ²⁄₈ inch is sufficient. In summer, owing to the oil being more fluid, there is sometimes a tendency to overflow the burner; but any inconvenience arising from it is avoided by the plan adopted in the Northern Lights, of shutting off the oil (by means of the apparatus already alluded to on p. 222) about fifteen minutes before extinguishing the lights in the morning.
Fig. 38.
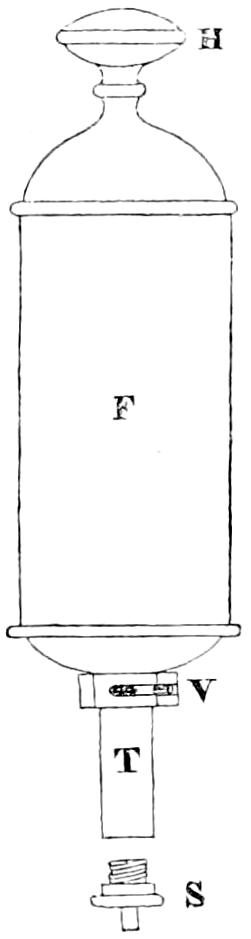
The arrangement for cutting off the oil is very simple, as will be seen from the annexed diagram (fig. 38), in which F is the fountain, T the oil-tube leading to the burner, and V the flow-hole, with its sliding valve. By turning the handle H one quadrant of the circle, the whole fountain F and tube T turn round their vertical axis, while the valve V, which rests in a notch in the cup of the lamp, remains still, and sliding over T, opens the flow-hole. S is the screw-plug which retains the oil in the fountain, and which is unscrewed and removed when the fountain is to be filled.
[226]
Fig. 39.
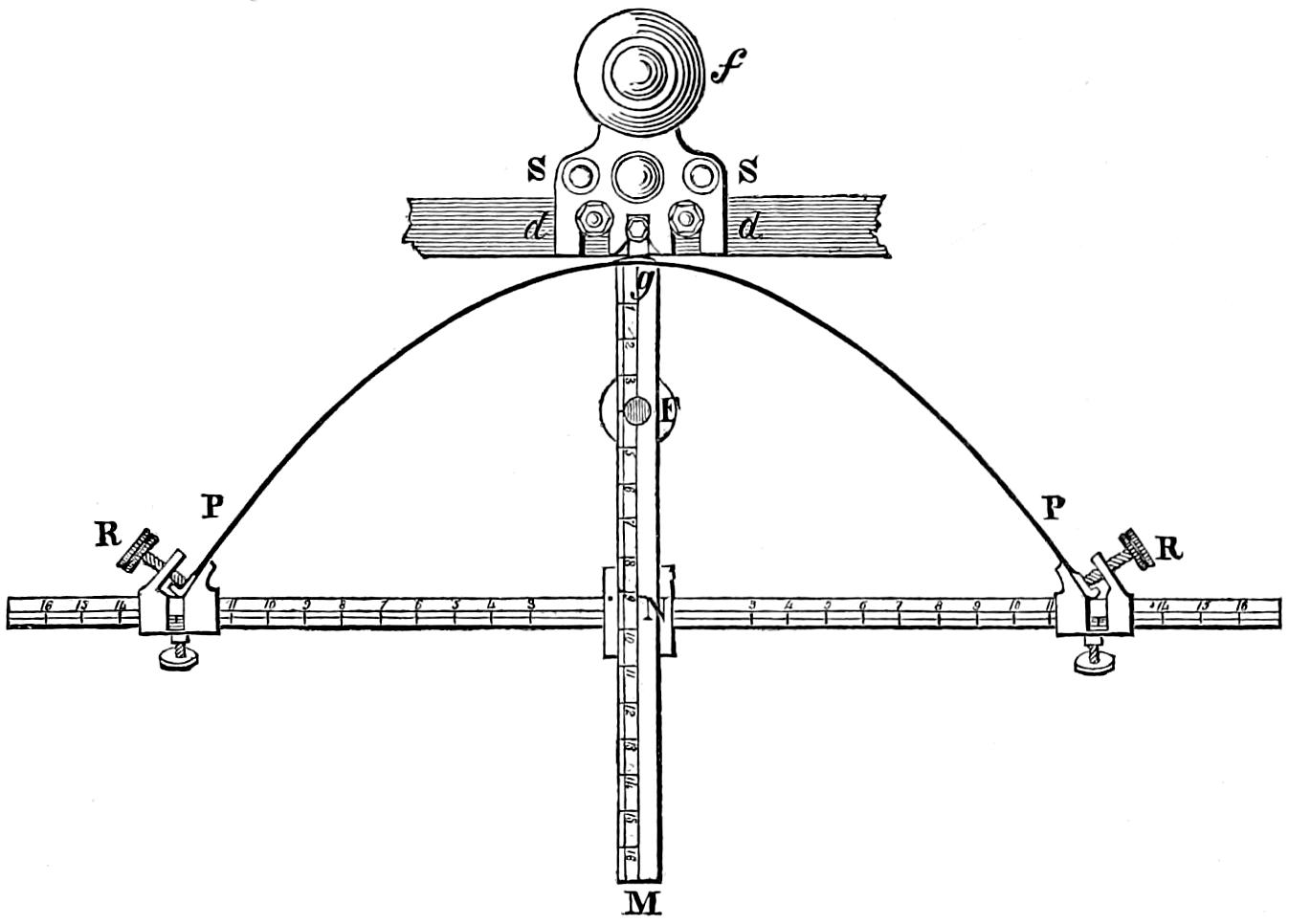
Fig. 40.
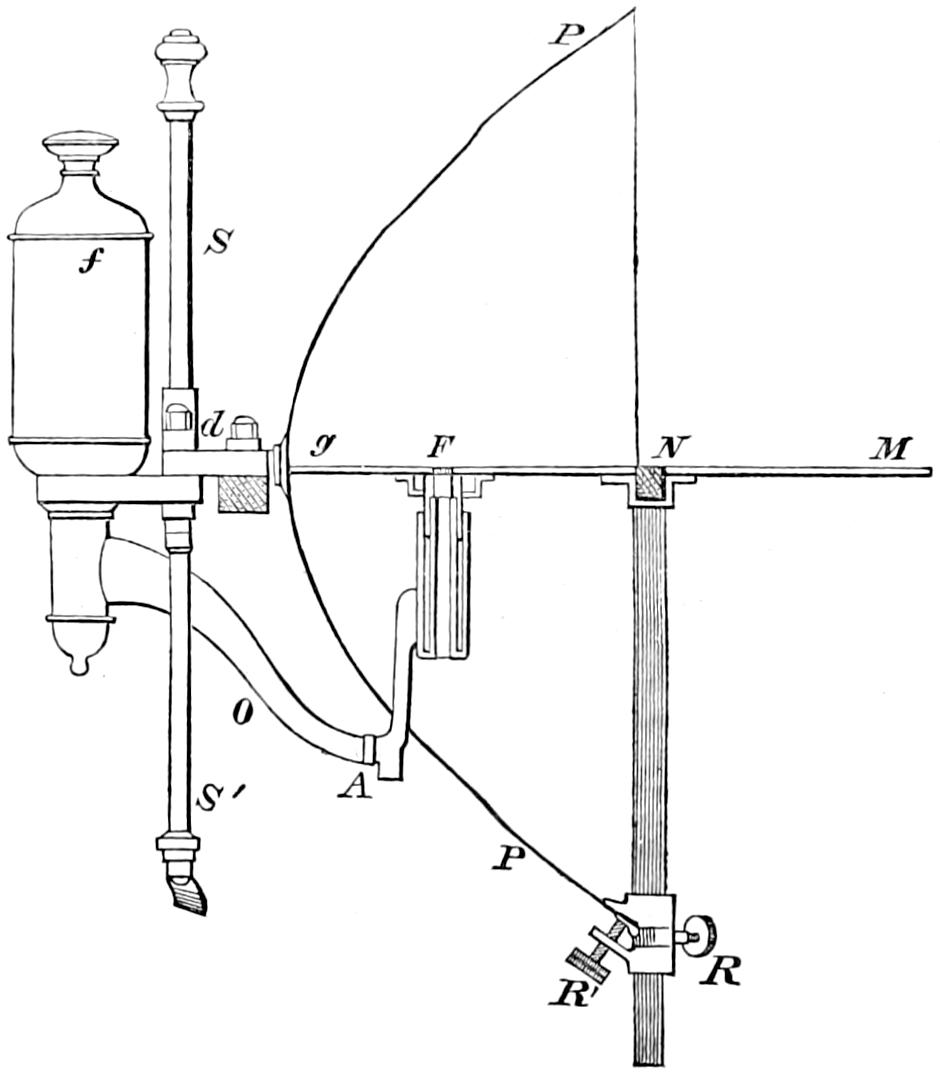
Placing the Lamp in the Focus. In the reflecting apparatus of the Northern Lighthouses, the focal position of the lamp is not, as we have already seen, liable to derangement, by the removal of the burner for the purpose of cleaning, as the sliding gear described at p. 221 insures the return of the lamp to its true place. The burner is originally set by means of a gauge, which touches four points of the mirror’s surface (one of them being its vertex, and the other three in the vertical plane of its greatest double ordinate). This gauge being provided with a short tube or collar properly placed for the purpose of receiving the burner, at once verifies its true position, both vertical and horizontal. The diagrams 39 and 40 shew the nature of the apparatus for adjusting the burners, the one being a plan and the other a section. The four points which touch the curve are one g at the vertex, two in the same horizontal plane with the focus, and near the edge of the mirror at PP, and[227] the fourth, also near the edge, and in the same vertical plane with the focus. F is the focus. The horizontal arms are graduated, and fitted with sliding pieces and clamping screws at R, so as to admit of being varied with the width of the mirror; but each gauge applies only to curves of the same focal distance; the distance F g being fixed. The gauge, when applied to the mirror, is properly secured by the screws at R, R, and R′; and the burner which is attached to the oil-tube in a temporary manner at A, is raised into the interior of the mirror. If the tube of the burner ascends into the circular tube at F until (when fixed by the checking handle already noticed at p. 221) its upper edge just touches a narrow projection inside the tube F (so placed that the rim of the burner should just touch it when it is on the level required for putting the brightest part of the flame in the focus), then the burner is in the proper position; but if, on the one hand, the axis of the burner stands beyond F, at some point between it and N (which lies in the plane of the mirror’s edge), the bent tube O from the fountain must be shortened at A; and if it rise too high, that tube must be bent down (and vice versa), until, by successive trials, it shall exactly fit into the tube F, and stand at the proper level. A skilful workman soon comes to guess those quantities very accurately; and, almost at the first trial, curtails the tube to the proper length, and bends it to the suitable level. All that is needful is to proceed cautiously, so as not to cut the tube too short, for this leads to some trouble.
The great advantage derived by seamen from the establishment of lights on a coast, soon makes the calls for additional lights so frequent, that their very number itself produces a new evil, in the difficulty of distinguishing the lights from each other. As the object of a light is to make known to the benighted mariner the land he has made, with as much certainty as the sight of a hill or tower would shew him his position during the day, it becomes an object of the first importance to Distinctions of Catoptric Lights. impress upon each light a distinctive character, which shall effectually prevent the possibility of its being mistaken for any other.
[228]
Catoptric lights are susceptible of nine separate distinctions, which are called fixed, revolving white, revolving red and white, revolving red with two whites, revolving white with two reds, flashing, intermittent, double fixed lights, and double revolving white lights. The first exhibits a steady and uniform appearance, which is not subject to any change; and the reflectors used for it (as already noticed) are of smaller dimensions than those employed in revolving lights. This is necessary, in order to permit them to be ranged round the circular frame, with their axes inclined at such an angle, as shall enable them to illuminate every point of the horizon. The revolving light is produced by the revolution of a frame with three or four sides, having reflectors of a larger size grouped on each side, with their axes parallel; and as the revolution exhibits once in two minutes, or once in a minute, as may be required, a light gradually increasing to full strength, and in the same gradual manner decreasing to total darkness, its appearance is extremely well marked. The succession of red and white lights is caused by the revolution of a frame whose different sides present red and white lights; and these, as already mentioned, afford three separate distinctions, namely, alternate red and white; the succession of two white lights after one red, and the succession of two red lights after one white light. The flashing light is produced in the same manner as the revolving light; but owing to a different construction of the frame, the reflectors on each of eight sides are arranged with their rims or faces in one vertical plane, and their axes in a line inclined to the perpendicular, a disposition of the mirrors which, together with the greater quickness of the revolution, which shews a flash once in five seconds of time, produces a very striking effect, totally different from that of a revolving light, and presenting the appearance of the flash alternately rising and sinking. The brightest and darkest periods being but momentary, this light is farther characterised by a rapid succession of bright flashes, from which it gets its name. The intermittent light is distinguished by bursting suddenly into view and continuing steady[229] for a short time, after which it is suddenly eclipsed for half a minute. Its striking appearance is produced by the perpendicular motion of circular shades in front of the reflectors, by which the light is alternately hid and displayed. This distinction, as well as that called the flashing light, is peculiar to the Scotch coast, having been first introduced by the late Engineer of the Northern Lights Board. The double lights (which are seldom used except where there is a necessity for a leading line, as a guide for taking some channel or avoiding some danger) are generally exhibited from two Towers, one of which is higher than the other. At the Calf of Man, a striking variety has been introduced into the character of leading lights, by substituting, for two fixed lights, two lights which revolve in the same periods, and exhibit their flashes at the same instant; and these lights are, of course, susceptible of the other variety enumerated above, that of two revolving red and white lights, or flashing lights, coming into view at equal intervals of time. The utility of all these distinctions is to be valued with reference to their property of at once striking the eye of an observer and being instantaneously obvious to strangers.
The introduction of colour, as a source of distinction, is necessary, in order to obtain a sufficient number of distinctions; but it is in itself an evil of no small magnitude; as the effect is produced by interposing coloured media between the burner and the observer’s eye, and much light is thus lost by the absorption of those rays, which are held back in order to cause the appearance which is desired. Trial has been made of various colours; but red, blue, and green alone have been found useful, and the two latter only at distances so short as to render them altogether unfit for sea-lights. Owing to the depth of tint which is required to produce a marked effect, the red shades generally used absorb from ⁴⁄₇ths to ⁵⁄₆ths of the whole light, an enormous loss, and sufficient to discourage the adoption of that mode of distinction in every situation where it can possibly be avoided. The red glass used in France absorbs[230] only ⁴⁄₇ths of the light; but its colour produces, as might be expected, a much less marked distinction to the seaman’s eye. In the Lighthouses of Scotland, a simple and convenient arrangement exists for colouring the lights, which consists in using chimneys of red glass, instead of placing large discs in front of the reflectors.
Fig. 41.
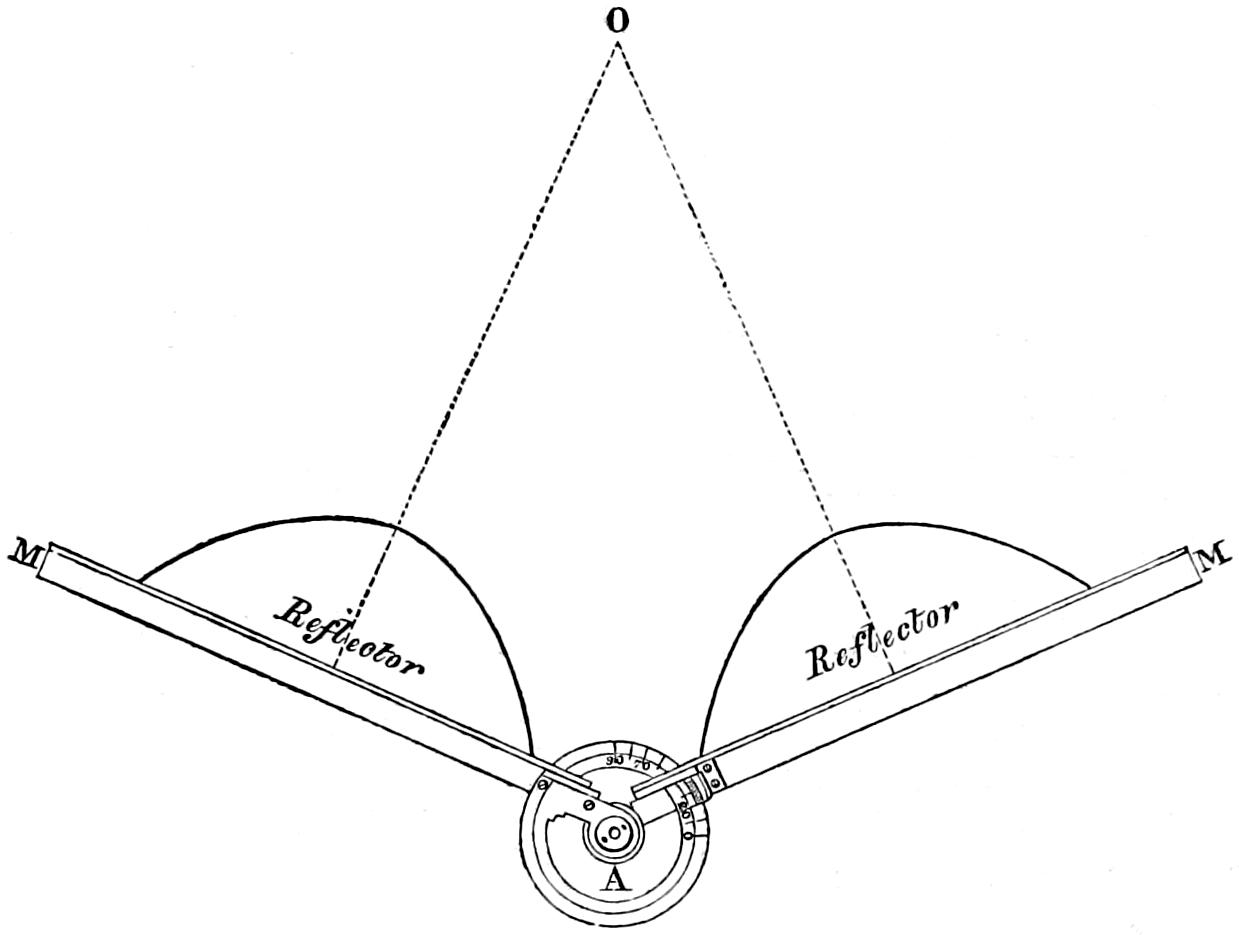
After what has been already said on the subject of divergence, it will at once be seen, that in revolving lights the reflectors are placed with their axes parallel to each other, so as to concentrate their power in one direction; whilst in fixed lights it is necessary, in order to approach as near as possible to an equal distribution of the light over the horizon, Arrangement of Reflectors on the Frame. to place the reflectors, with their axes inclined to each other, at an angle somewhat less than that of the divergence of the reflected cone. For this purpose, a brass gauge (see fig. 41), composed of two long arms, AM, AM, somewhat in the form of a pair of common dividers, connected by a means of a graduated limb A, is employed. The arms having been first placed at the angle, which is supplemental to that of the inclination of the axes of the two adjacent mirrors at O, are made to span the faces of the reflectors, one of which is[231] moved about till its edges are in close contact with the flat surface of one of the arms of the gauge.
Fig. 42.
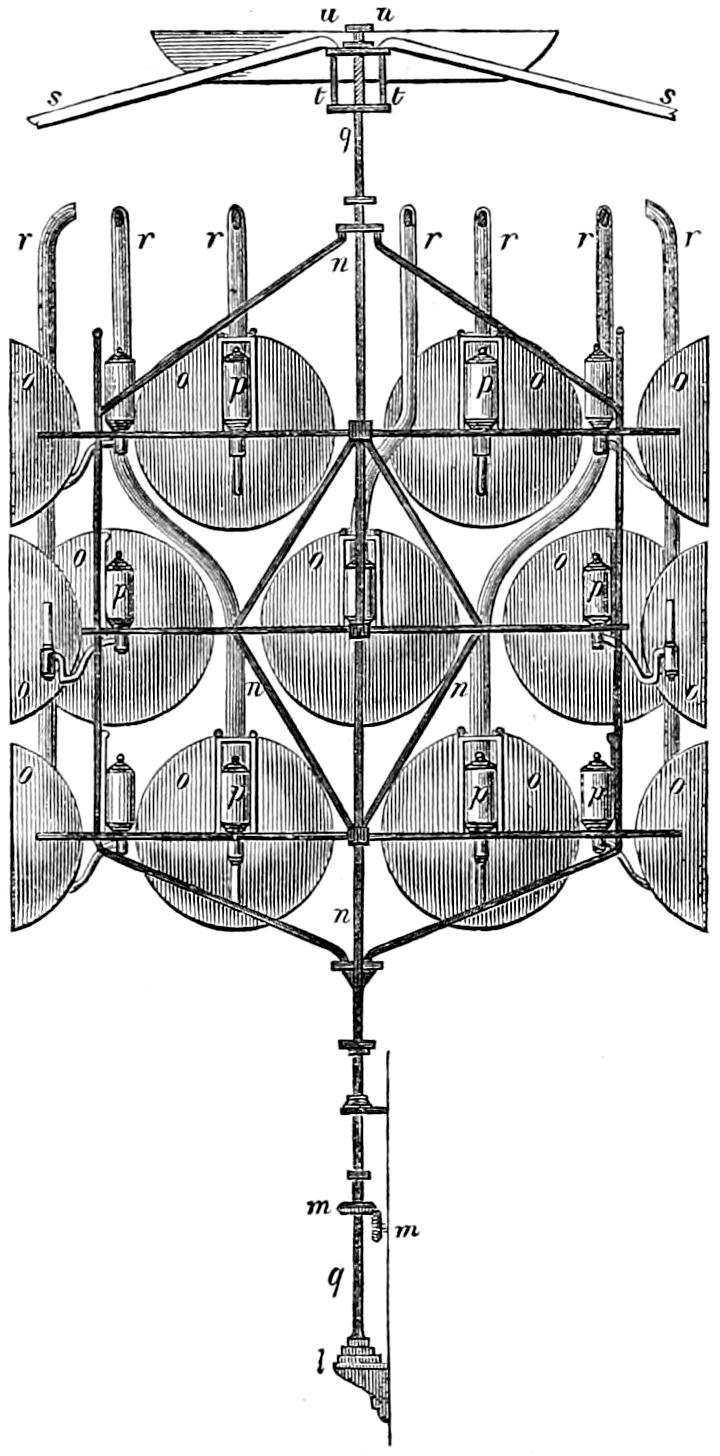
Fig. 43.
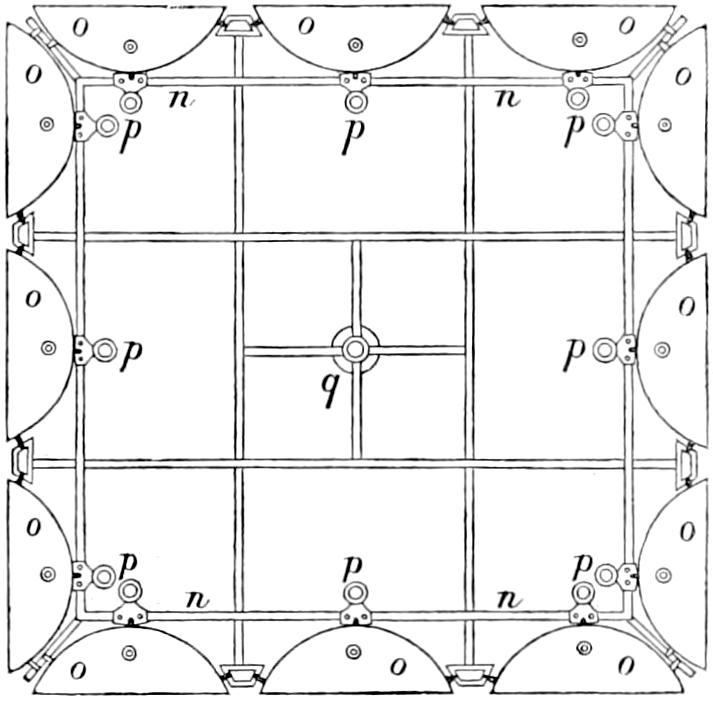
Figs. 42 and 43 shew an elevation and plan of a revolving apparatus on the catoptric principle. In these figures, n n shews the reflector frame or chandelier; o o, the reflectors with their oil-fountains p p. The whole is attached to the revolving axis or shaft q. The copper tubes r r convey the smoke from the lamps; s s are cross bars which support the shaft at t t; u u is a copper pan for receiving any moisture which may accidentally enter at the central ventilator in the roof of the light-room; l is a cast-iron bracket, supporting the cup in which the pivot of the shaft turns; m m are bevelled wheels, which convey motion from the machine to the shaft. The machinery does not require any particular notice, being that of common clock-work, moved by the descent of a weight.
[232]
Fig. 44.
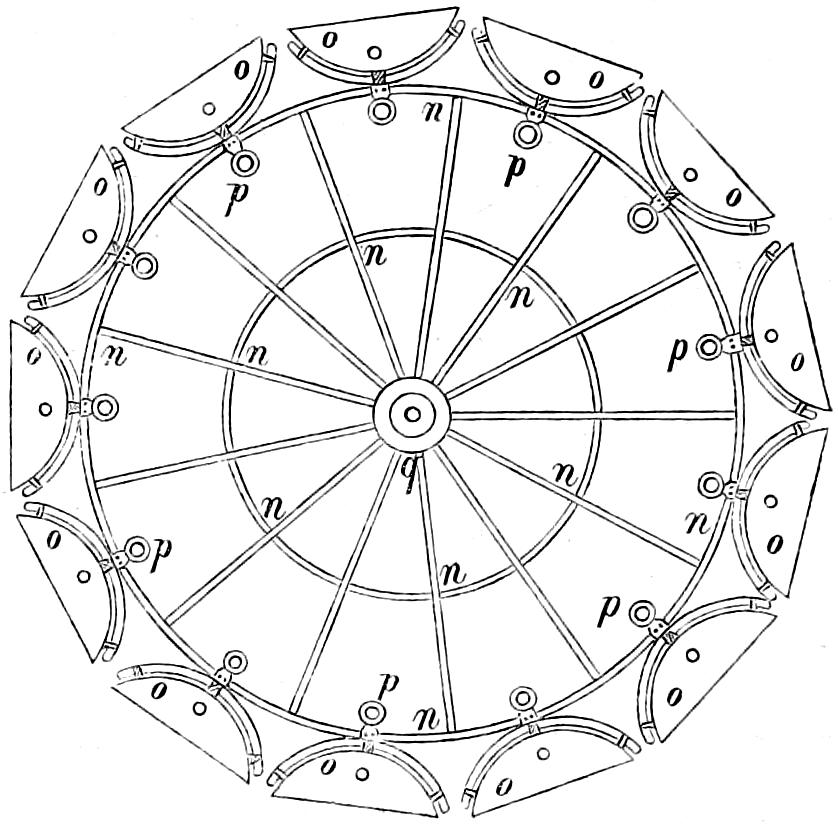
Fig. 44 shews a plan of one tier of reflectors arranged in the manner employed in a fixed catoptric light; n n shews the chandelier, q the fixed shaft in the centre, which supports the whole, o o the reflectors, and p p the fountains of their lamps. In this figure (in order to prevent confusion) only one tier of reflectors is shewn; the other tiers are so arranged, that their axes divide into equal angles the arcs intercepted between the axes of the adjoining reflectors on the first tier, thereby producing the nearest approach to an equal distribution of the light, which is attainable by this arrangement.
In lighthouses of moderate height, the proper position for the reflector itself is perfect horizontality of its axis, which may be ascertained with sufficient accuracy, by trying with a plummet, whether the lips of the instrument, which we may conclude to be at right angles to the plane of its axis, be truly vertical. In lightrooms very much elevated above the sea, however, the dip of the horizon becomes notable; and a slight inclination forwards should be given to the face of the reflectors, so that their axes produced may be tangents to the earth at the visible horizon of the light-room. This, however, must not be permitted to interfere with the perfect horizontality of the top of the burner, which is indispensable to its proper burning.
Bordier Marcet’s Reflectors. Various forms of the parabolic mirror were invented by M. Bordier Marcet, the pupil and successor of Argand, who has laboured with much enthusiasm in perfecting catoptric instruments, more especially with a view to their application in the illumination of lighthouses and the streets of towns. Amongst many other ingenious combinations, he has invented and constructed an apparatus which is much used in harbour-lights on the French coast,[233] where it is known by the fanciful name of Fanal Sidéral. Fanal[46] sidéral. The object is to fulfil, as economically as possible, the conditions required in a fixed light, by illuminating, with perfect equality, every part of the horizon, by means of a single burner; and M. Bordier Marcet has in his work-shop an instrument of this kind, eight feet in diameter, which he constructed on speculation. The apparatus used in harbour-lights, on the French coast, is of much smaller dimensions, and does not exceed fifteen inches in diameter. A perfect idea of the construction and effect of this instrument may be formed, by conceiving a parabola to revolve about its parameter as a vertical axis, so that its upper and lower limbs would become the generating lines of two surfaces possessing the property of reflecting, in lines parallel to the axis of the parabola, all the rays incident upon them, from a light placed in the point where the parameter and axis of the generating parabola intersect each other. This point being the focus of each parabolic section of this apparatus, light is equally dispersed in every point of the horizon, when the axis of the parabolic section is in a plane perpendicular to a vertical line. But however perfectly this apparatus may attain its important object, it necessarily produces a feeble effect; because as its action is entirely confined to the vertical direction, the light distributed by it decreases directly as the distance of the observer. This beautiful little instrument is shewn at fig. 45, in which b shews the burner, p p the upper reflecting surface, and p′ p′ the lower reflecting surface, both generated in the manner above described by the revolution of a parabola about its parameter x b; F is the focus of the generating parabola; and l l are small pillars, which connect the two reflecting plates, and give strength to the apparatus.
[46] Fanal, from φανεν, a lantern.
Fig. 45.
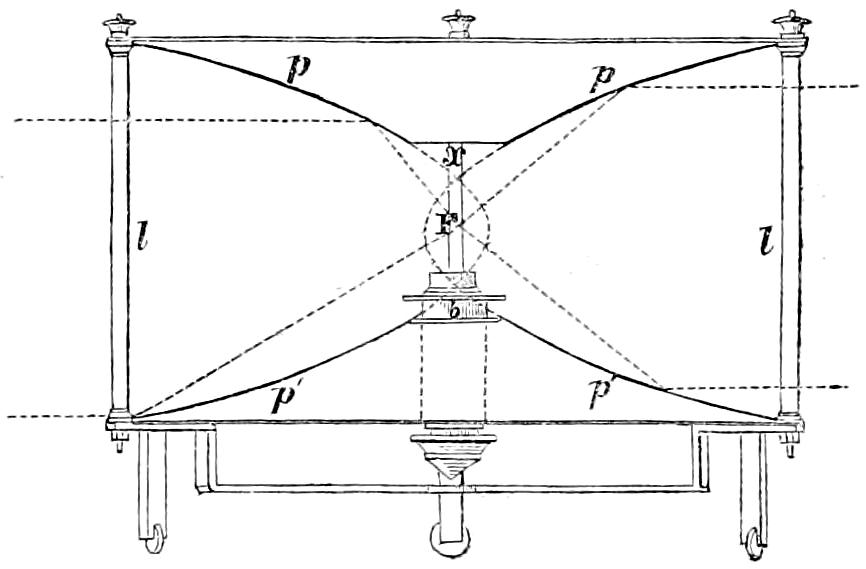
[234]
M. Bordier Marcet has also prepared an ingenious modification of the paraboloïdal mirror, which he has described under the name of Fanal à double effet. fanal à double effet; and the object of which is to obtain a convenient degree of divergence from parabolic mirrors, by the use of two flames and two reflecting surfaces, each of which is acted upon by its own flame, and also by that of the other. This modification consists in the union of two portions of hollow paraboloïdal mirrors, generated by the revolution of two parabolas about a common horizontal axis, and illuminated by two lamps placed in the focus of each. The first surface is generated by the revolution on its axis of a segment of a paraboloid intercepted between the parameter and some double ordinate greater than it, and may, from its form, be called the ribbon-shaped mirror. The second surface is that of a parabolic conoid, which is cut off by a vertical plane passing through a double ordinate, which is equal to the parameter of the parabolic ribbon, which is placed in front of it. The elements of the curve which forms the conoïdal mirror, must be so chosen as to have its focus at a convenient distance in front of that of the ribbon-shaped mirror, so as to admit of placing the two lamps separate from each other, as well as to produce the necessary degree of divergence, which is to be obtained by the action of these mirrors respectively on the flame placed in the focus of the other. These two mirrors are joined together in the line of the parametric section of the ribbon, which coincides with the lips of the conoid at some double ordinate behind its parameter. Each mirror produces, by means of the lamp placed in its focus, an approach to parallelism of the reflected rays, which M. Bordier Marcet has not inaptly termed the principal effect; whilst the action of each surface on the lamp which is placed in the focus of the other, causes what the inventor calls the secondary or lateral effect. Their secondary action may be described thus: The lamp, which is in the focus of the ribbon, is much nearer the vertex of the conoid than its own focus; so that its rays making, with normals to the surface of the conoid, angles greater than those which are formed by the rays proceeding from its focus, are of necessity reflected[235] in lines diverging from the axis of the mirror. Those, on the contrary, which proceed from the focus of the conoid, meet the ribbon-shaped surface, so as to make angles with its normals more acute than those which the rays from its own focus could do, and which are, therefore, reflected in lines converging to the axis of the mirror. Those reflected rays must therefore cut the axis, and diverge from it on the other side. This apparatus has been used at La Hève and some other lights on the French coast; but it is impossible not to perceive the great loss of light which results from the use of two flames in one mirror; and it must not be forgotten, that the divergence which is obtained by means of it is not confined to the horizontal direction in which only it is wanted; but that the light is at the same time scattered in every direction round the edge of the mirror.
Arrangements of a similar kind were proposed and executed for the same purpose of uniting greater divergence with considerable power in the central parts of the resultant beam, by Argand himself, in 1806, and also in 1808, by M. Haudry, Ingénieur des Ponts et Chaussées. Argand proposed the union of a paraboloid, and an ellipsoid having their foci coincident in one point, which being the posterior focus of the latter curve, was illuminated by the rays reflected to it by means of the ellipsoïdal surface from the lamp placed in the anterior focus. From the optical focus thus obtained, some rays would fall on the paraboloïdal surface and produce, by reflection, a cylinder of parallel rays, while the rest would diverge from the axis, and form a zone of spreading rays. M. Haudry’s plan consisted of a combination of a conical with a paraboloïdal mirror, so placed, that the rays from the front part of the hollow cone might be nearly parallel to those sent out by the paraboloid; while the rays from its base diverging from the axis might produce a ring of divergent rays, similar to that obtained from the ellipsoid of Argand’s apparatus.
It would occupy much time to exhibit all the disadvantages of the arrangements in the fanal à double effet of M. Bordier Marcet,[236] and also in those of Argand and Haudry; and I shall therefore dismiss the subject by observing, that the loss of light due to the position of the flame in the apparatus of Argand, is so great as to induce one to wonder that such combinations should ever have been attempted. There can be no doubt, that the most efficient mode of obtaining due divergence from mirrors, is to adopt the paraboloid, with a short focal distance, which has the double advantage of increasing the divergence which is due inversely to the focal distance, and, at the same time, subjecting to the action of the mirror a larger portion of the luminous sphere proceeding from the flame.
Fig. 46.
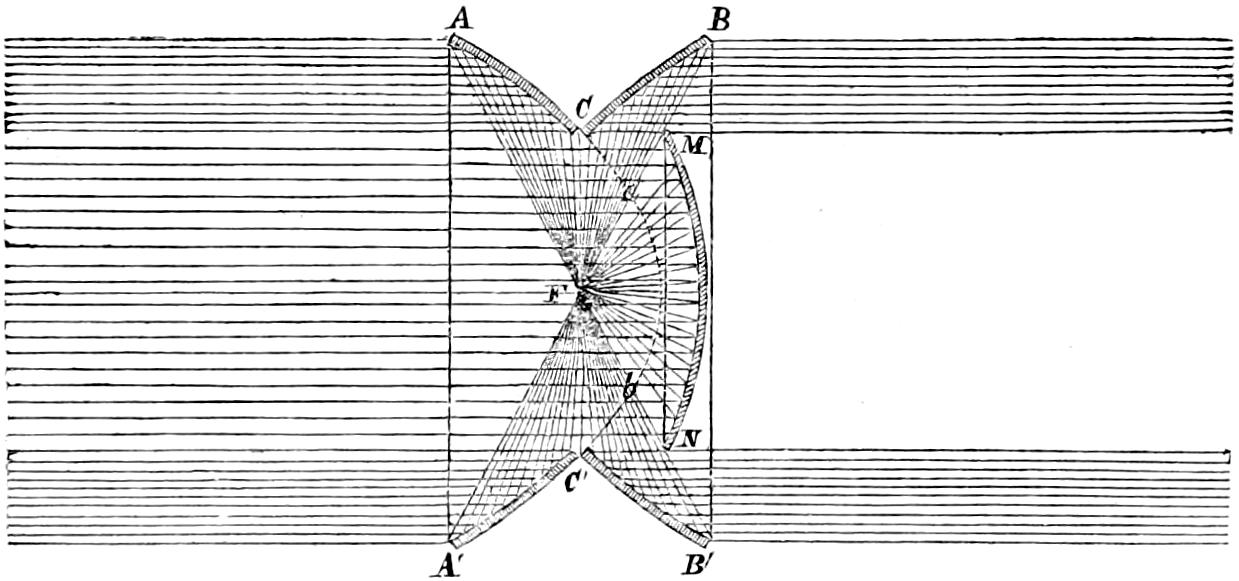
Fanal à double face. Lastly, I shall notice M. Bordier Marcet’s fanal à double face, which consists of two paraboloïdal mirrors, truncated in the vertical plane of the parameter, and united together back to back, so as to be illuminated by the same lamp placed in their common focus. To save the light which would otherwise escape the catoptric action, he adds a parabolic conoid of greater focal distance, and so placed, that while its focus may coincide with the common focus of the other mirrors, its size may be so restricted, that it shall not interfere with the effect of the truncated mirror opposite which it is placed. The obvious consequence of such an arrangement is, that the rays (see fig. 46) produced from a lamp in the common focus of the three mirrors, will produce in opposite directions a luminous ring from each of the truncated mirrors AC, BC, and A′C′, B′C′, while the central or conoïdal mirror MN will fill the interior of one of those luminous rings with a cone of rays, whose intensity will be in the inverse[237] ratio of MN² to a b² (or FM² to F a²), which latter surface represents the whole amount of naturally divergent rays, which strike on a b, and which are spread over MN. Two sets of reflectors of this form facing in opposite directions (each set arranged in one plane, and fixed on a frame which could be made to revolve round a vertical axis), would thus present their brightest effect after considerable intervals of darkness; but, by arranging them with their axes slightly inclined, they were made to prolong the light periods and curtail the dark ones. M. Bordier Marcet speaks of this apparatus with all the satisfaction generally felt by inventors; but it is no difficult matter to identify its effect with that of the common paraboloïdal mirrors. It is obvious, that all the rays which fall from a true focal point on the three reflectors AC, BC, A′C′, B′C′, and MN, are merely those which would fall on a single reflector, whose double ordinate and the portion of the abscissa between that ordinate and the focus, are equal to those of the first reflector of the compound system, so that the quantity of light reflected by the three reflectors is neither more nor less than that which would be projected by one. All the difference that can exist is, that in the case of a flame which has a notable size, the surface MN being farther distant than a b, would produce less aberration and, consequently, a very slight increase of intensity in the small portion of the reflected beam of parallel rays due to that part of the compound mirror. We cannot, therefore, sensibly err in rejecting any advantage to be derived from this arrangement as insignificant.[47]
[47] See Peclet′s Traité de l′Eclairage, p. 302, from which fig. 46 is copied.
Spherical mirrors have been employed in Lighthouses chiefly when they can be introduced to aid the effect of refracting apparatus: and it will not be necessary to say much of them in this place. I must, however, notice an ingenious proposal of Mr Barlow′s Spherical Mirrors. Mr W. H. Barlow,[48] who suggests placing in front of the flame a small spherical reflector, whose centre is coincident with the focus of a paraboloïd,[238] and whose subtense is the parameter of the generating curve. The small mirror, being somewhat less than a hemisphere, would cause the light falling upon it to be returned through the focus so as to reach the paraboloïdal surface and to be finally reflected from that portion of it which is embraced between the limits of its extreme divergence. If there were no loss of light at the surface of the small mirror, its effect would be to increase the power of the beam of parallel rays by an amount equal to the sum of the rays incident on the spherical surface, but at the same time to diminish it by intercepting a portion of the light reflected from the paraboloïd. I am not aware that such a combination has been tried, as it applies most advantageously to reflectors whose span does not exceed the parameter of the generating curve, a form rarely adopted in lighthouses; but it might also be adapted to reflectors which intercept a larger portion of light, by making the spherical reflector some segment less than the hemisphere.
[48] In an excellent paper above noticed, on the Illumination of Lighthouses, in the London Transactions, for 1837.
Captain Smith’s Mirrors in the form of a parabolic spindle. Captain Smith of the Madras Engineers, has described in the “Professional papers of the ‘Corps of Royal Engineers,’[49] a new system of fixed lights,” which consists in placing a flat wick in the focus of one-half of a hollow parabolic spindle generated by the rotation of a parabola about its parameter as a vertical axis. The action of the instrument is obvious, for each vertical section being parabolic, effects a change only in the vertical divergence of the rays incident on it from the focus, and suffers their horizontal direction to remain unaltered; thus each vertical plate of reflected rays passes through the parameter of the curve and illuminates the opposite point of the horizon by means of a narrow strip or line of light. Two hollow spindles of that form, each lighting 180° and facing opposite azimuths, would, therefore, be sufficient to illuminate the whole horizon. The author of the paper, however, appears to contemplate the employment of a series of those mirrors ranged one above another and breaking joint vertically, somewhat in the manner already described in speaking of the arrangement of the paraboloïdal[239] mirrors used in fixed lights. The advantages of this mode of illumination are much overrated by Captain Smith, who seems to magnify beyond its real importance the risk attending the use, in the dioptric apparatus, of a single lamp, whose sudden extinction would deprive at once the whole horizon of the benefit of the light; while, on the contrary, he reckons the security obtained by his arrangement as an advantage of the highest value. In certain situations, where no regular establishment of trained light-keepers is maintained, that security may be an object of more importance and may warrant a greater sacrifice, than is necessary in Great Britain; but I have no hesitation in saying, that I know of no situation in which the plan proposed by Captain Smith could bear comparison with the mode of illumination for fixed lights by means of the catadioptric instruments of Fresnel.
[49] Vol. v., p. 56.
[50] Most probably directly derived from the Greek διόπτρον, an optical instrument with holes for looking through, whose name is a compound of διὰ, through, and ὄπτομαι, I see.
One of the earliest notices of the application of lenses to lighthouses is that recorded by Smeaton in his Narrative of the Eddystone Lighthouse, where he mentions a London optician, who, in 1759, proposed grinding the glass of the lantern to a radius of seven feet six inches; but the description is too vague to admit of even a conjecture regarding the proposed arrangement of the apparatus. About the middle of the last century, however, lenses were actually tried in several lighthouses in the south of England, and in particular at the South Foreland in the year 1752; but their imperfect figure and the quantity of light absorbed by the glass, which was of impure quality and of considerable thickness, rendered their effect so much inferior to that of the parabolic reflectors then in use, that after trying some strange combinations of lenses and reflectors, the former were finally abandoned. Lenses were also tried at the lights[240] of Portland, Hill of Howth, and Waterford, by Mr Thomas Rogers, a glass manufacturer in London; who possessed, it is said, the art of blowing mirrors of glass, “and by a new method silvered over the convex side without quicksilver.”[51]
[51] Hutchinson’s Practical Seamanship, p. 200. See also the notice of the spherical mirrors made by Messrs François and Letourneau of Paris in a subsequent part of this volume.
The object to be attained by the use of lenses in a Lighthouse is, of course, identical with that which is answered by employing reflectors; and both instruments effect the same end by different means, collecting the rays which diverge from a point called the focus, and projecting them forward in a beam, whose axis coincides with the produced axis of the instrument. We have already seen that, in the case of reflection, this result is produced by the light being thrown back from a surface so formed as to make all the rays to proceed in one and the same required direction. In the case of refraction, on the other hand, the rays pass through the refracting medium, and are bent or refracted from their natural course into that which is desired.
The celebrated Buffon, to prevent the great absorption of light by the thickness of the material, which would necessarily result from giving to a lens of great dimensions a figure continuously spherical, proposed to grind out of a solid piece of glass, a lens in steps or concentric zones. This suggestion of Buffon regarding the construction of large burning glasses, was first executed, with tolerable success, about the year 1780, by the Abbé Rochon; but such are the difficulties attending the process of working a solid piece of glass into the necessary form, that it is believed the only other instrument ever constructed in this manner, is that which was made by Messrs Cookson of Newcastle-upon-Tyne, for the Commissioners of Northern Lighthouses.
The merit of having first suggested the building of lenses in separate pieces, seems to be due to Condorcet, who, in his Eloge de Buffon, published so far back as 1773, enumerates the advantages to be derived from this method. Sir David Brewster also described[241] this mode of building lenses in 1811, in the Edinburgh Encyclopædia; and in 1822, the late eminent Fresnel, unacquainted with the suggestions of Condorcet or the description by Sir David Brewster, explained, with many ingenious and interesting details, the same mode of constructing those instruments. To Fresnel belongs the additional merit of having first followed up his invention, by the construction of a lens and, in conjunction with MM. Arago and Mathieu, of placing a powerful lamp in its focus, and indeed of finally applying it to the practical purposes of a Lighthouse.
The great advantages which attend the mode of construction proposed by Condorcet are,—the ease of execution, by which a more perfect figure may be given to each zone and spherical aberration in a great measure corrected, and the power of forming a lens of larger dimensions than could easily be made from a solid piece. Both Buffon and Condorcet, however, chiefly speak of reducing the thickness of the material, and do not seem to have thought of determining the radius and centre of the curvature of the generating arcs of each zone, having contented themselves with simply depressing the spherical surface in separate portions. Fresnel, on the other hand, determined those centres, which constantly recede from the vertex of the lens in proportion as the zones to which they refer are removed from its centre; and the surfaces of the zones of the annular lens, consequently, are not parts of concentric spheres, as in Buffon’s lens. It deserves notice, that the first lenses constructed for Fresnel by M. Soleil had their zones polygonal, so that the surfaces were not annular, a form which Fresnel considered less accommodated to the ordinary resources of the optician. He also, with his habitual penetration, preferred the plano-convex to the double-convex form, as more easily executed.[52] After mature consideration, he finally adopted crown glass, which, notwithstanding its greenish colour, he preferred to flint glass, as being more free from[242] striæ. All his calculations were made in reference to an index of refraction of 1·51, which he had verified by repeated experiments, conducted with that patience and accuracy for which, amidst his higher qualities, he was so remarkably distinguished.[53] The instruments have received the name of annular lenses, from the figure of the surface of the zones.
[52] The plano-convex lens, with its curved side towards the parallel rays, is also a form producing small spherical aberration, a circumstance which may also have influenced his choice.
[53] My friend, Mr William Swan, carefully examined, by his new and ingenious method, described in the Edinburgh New Philosophical Journal, January 1844, several specimens of the St Gobain glass (which is now used in the manufacture of the lenses), and found its refractive index to be 1·51793, the difference between the greatest and least values being only 0·00109.
A ray of light, in passing obliquely from one transparent body into another of different density, experiences at the point of the intersection of the common surface of the two planes, a sudden change of direction, to which the name of Refraction. refraction has naturally been given, in connection with the most familiar instance of the phenomenon, which is exhibited by a straight ruler with one half plunged into a basin of water while the other remains in the air. The ruler no longer appears straight, but seems to be bent or broken at the point where it enters the water. It may not be out of place to call attention to the laws which regulate the change of direction in the incident light, which are three in number.
1. Incidence and refraction, in uncrystallized media of homogeneous structure such as glass, always occur in a plane perpendicular to that of the refracting surface.
2. In the same substances, the angle formed with the perpendicular by the ray at its entering the surface of the second medium, has to the angle which it makes with the normal after it has entered the surface, such a relation, that their sines have a fixed ratio, which is called the refractive index. When a ray falls normally on the surface of any substance, it suffers no refraction.
3. The effect of passing from a rare to a dense medium, as from air into water or glass, is to make the angle of refraction less than the angle of incidence; and those angles are measured with reference[243] to a normal to the plane which separates the media at the point of incidence. The converse phenomenon, of course, takes place in the passage from a dense to a rare medium, in which case the angle of incidence is less than the angle of refraction. To this rule there are a few exceptions; for there are certain combustible bodies, such as diamond, whose refractive powers are much greater than other substances of equal density.
Fig. 47.
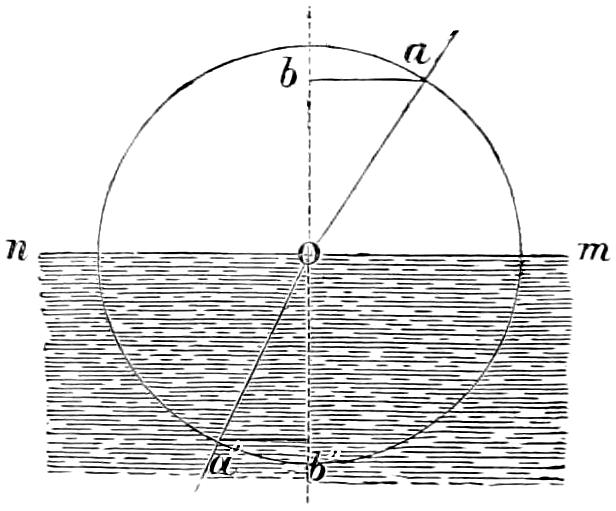
The diagram (fig. 47) will serve to render those laws more intelligible. Let a ray of light a O meet a surface of water n m at O, it will be immediately bent into the direction O a′; and if, from the centre O, we describe any circle, and draw a line b O b′, perpendicular to nm; then ab and a′ b′, perpendiculars drawn to the normal bb′, from the points a and a′ where the circle cuts the incident and refracted rays, will be the sines of the angle of incidence b O a, and of the angle of refraction b′ O a′, and the ratio of those sines to each other, or b ab′ a′ will be the relative index of refraction for the two media.
4. It may perhaps be added, for convenience, as a fourth law, deducible from the others, that since rays passing from a dense into a rare medium, have their angle of refraction greater than the angle of incidence, there must be some angle of incidence whose corresponding angle of refraction is a right angle; beyond which no refraction can take place, because there is no angle whose sine can be greater than the radius. In such circumstances, total reflection ensues. For common glass, whose index of refraction is 1·5, we have (in the case of emergent rays) sine of incidence = sine of refraction1·5; but, as no sine can exceed radius or unity, the angle of incidence must be limited to 41° 49′; beyond which total reflection will take place, and the light will return inwards into the glass, being reflected at its surface.
[244]
Thus, if a ray proceed from a point O (fig. 48), within a piece of glass, to a point C, at its surface A B; and if O C b, its incidence, be less than 41° 49′, it will be refracted in some direction C f; but if this angle be greater than 41° 49′, as O C′ b′, the ray will be reflected back into the glass in the direction C′ O′.
Fig. 48.
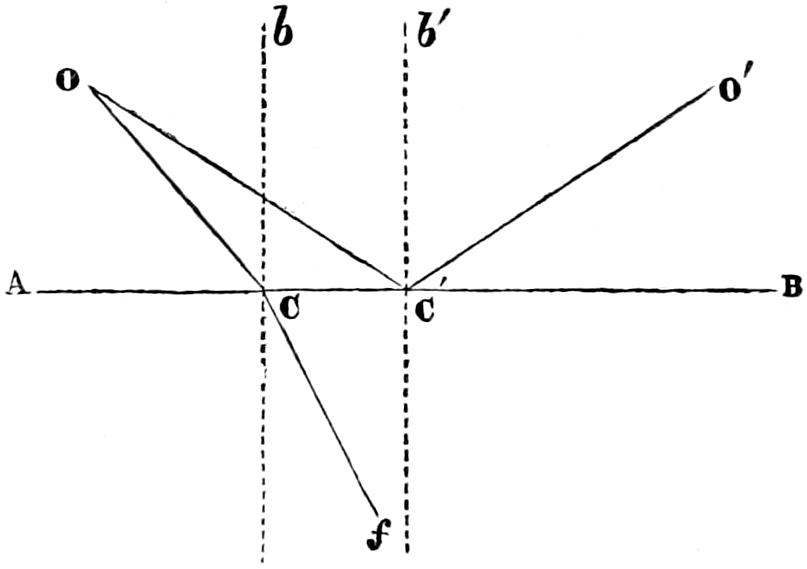
The material hitherto employed in the construction of lighthouse apparatus is crown glass, which, although it possesses a lower refractive power than flint glass and has, besides, a slightly greenish tinge, offers the great practical advantages of being more easily obtained of homogeneous quality; and, being less subject to deterioration from atmospheric influences, it is peculiarly suitable for use in the exposed situations generally occupied by Lighthouses. The refractive index of crown glass, as already noticed, is about 1·5.
Any one may easily satisfy himself by a careful protraction of the angles of incidence and refraction, in the manner above described, as to the truth of the following general propositions resulting from those laws:—
1. A ray of light passing through a plate of some diaphanous substance such as glass, with parallel surfaces, suffers no change of direction, but emerges in a line parallel to its original path, merely suffering a displacement, depending on the obliquity of the incident ray, and the refractive power and thickness of the plate. The effect of this displacement is merely to give the ray an apparent point of origin different from the true one. This will be easily understood by the diagram (fig. 49), in which a b is a normal to the plate, whose surfaces x x and x′ x′ are parallel, r r r r shews the path of the ray, r r the displacement, and r′ the apparent point of origin resulting from its altered direction.
Fig. 49.
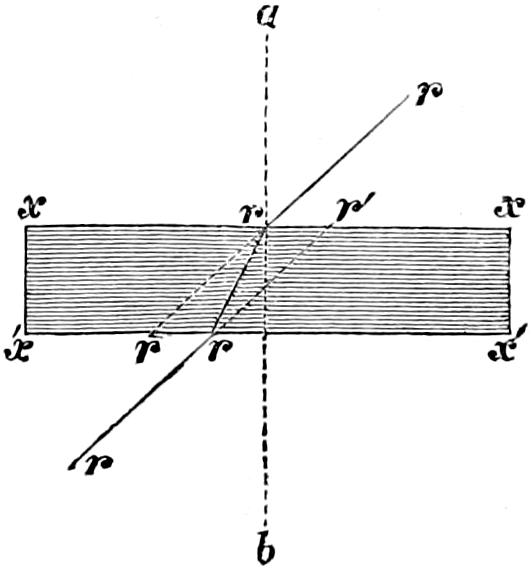
[245]
2. When a ray passes through a triangular prism a b c, the inclination of the faces a c and c b causes the emergent ray r′ to be bent towards a b, the base of the prism, in a measure depending on the inclination of the sides of the prism and the obliquity of the incident ray to the first surface.
Fig. 50.
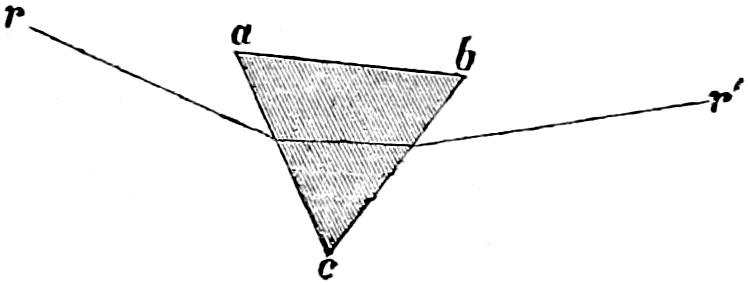
3. When parallel rays fall on a concave lens, they will, at their emergence, be divergent. The section of the diaphanous body a b c d may be regarded as composed of innumerable frusta of prisms, having their apices directed towards the centre line x r; and the rays which pass through the centre, being normal to the surface, will be unchanged in their direction, while all the others will (as shewn in the figure) suffer a change of direction, increasing with their distance from the centre, owing to the increasing inclination of the surfaces of the lens as they recede from its axis.
Fig. 51.
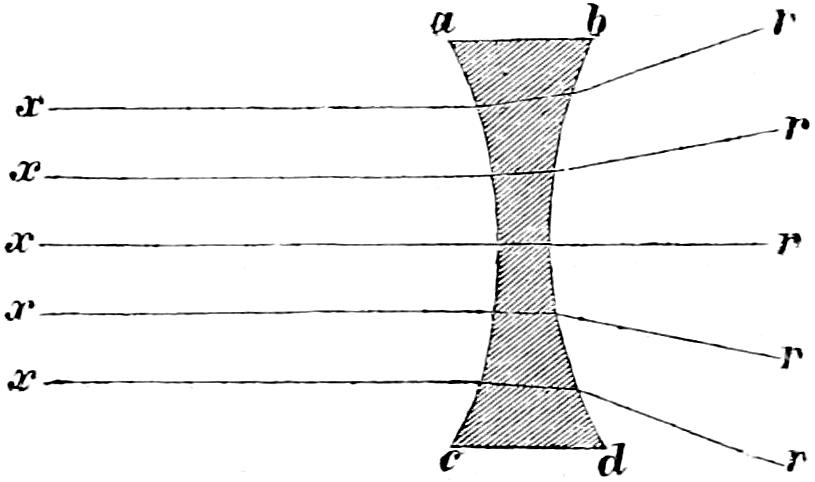
4. Lastly, when divergent rays fall on a convex lens a b, from a point f, called the principal focus, they are made parallel at their emergence; while, conversely, parallel rays which fall on the lens are united in that point.[54] This effect, which is the opposite of that caused by the concave lens, may be explained in a similar manner, by conceiving the section a b of the convex lens to be composed of innumerable frusta of prisms, arranged with their bases towards the centre of the lens.
[54] It is, of course, to be understood that only rays incident near the axis of the lens are refracted accurately to a focus.
Fig. 52.
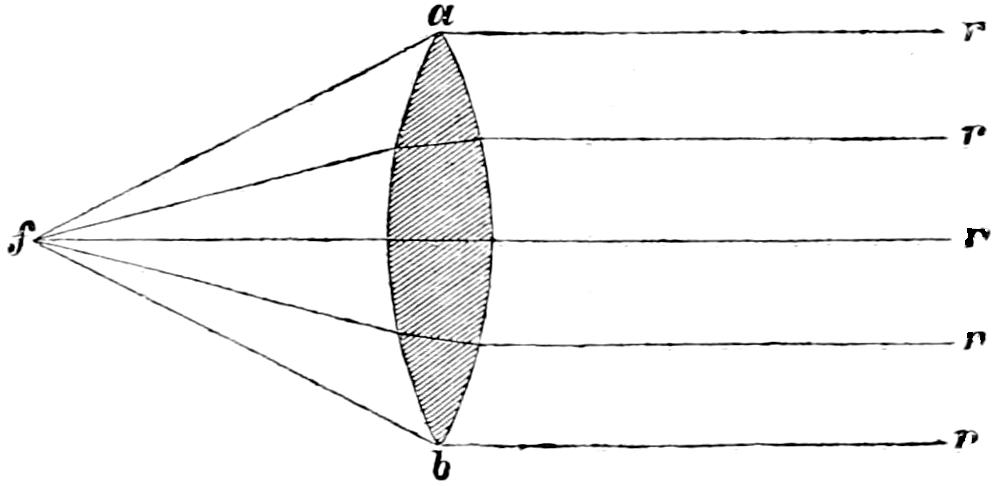
[246]
Now, it is obvious, that we can derive no assistance, in economising the rays of a lamp for Lighthouse purposes, from concave lenses, whose property is to increase the dispersion of the rays incident on them. With concave lenses, therefore, we have no concern; and we shall confine ourselves to the consideration of the convex or converging lenses.
The lens always used in Lighthouses is (for reasons already noticed) plano-convex, and differs from the last only by having a plane and a curve surface, instead of two curve surfaces, whose radii are on opposite sides of the lens. The plano-convex is generally regarded, by writers on optics, as a case of the double convex having one side of an infinite radius. Both forms cause parallel rays to converge to a focus.
We commence with a general view of the relations which exist between the position of the radiant and the focus.
Fig. 53.
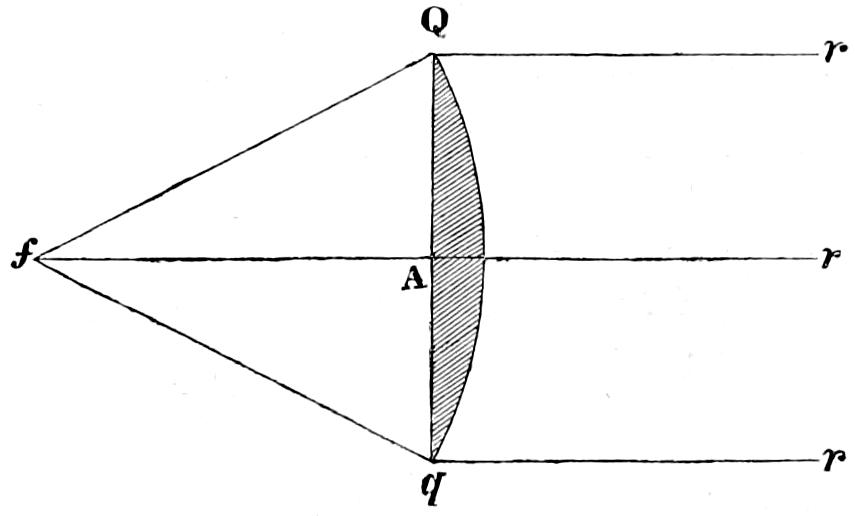
Let Q q be a section of a lens, and f A r its optical axis, or the line in which a ray of light passes unchanged in its direction through the lens, from its being normal to both surfaces, whether the lens be double-convex as above, or plano-convex (see fig. 53), then the principal focus f is that point where the rays from r r r, which fall parallel to the optic axis on the outer face of the lens, meet after refraction at the two faces,—or, to speak more in the language of the art which is under consideration, the principal focus f is the point whence the rays of light, proceeding in their naturally divergent course, fall on the inner surface Q A q of the lens, and are so changed by refraction there and at the outer face, that they finally emerge parallel to the optic axis in the directions Q r, q r. The position of this point depends partly on the refractive power of the substance of which the lens is composed and partly on the curvature of the surface or surfaces which bound it.
[247]
It would be quite beyond the scope of these Notes to attempt to present the subject of refraction at spherical surfaces before the reader’s view in a rigorous or systematic manner, and thus to advance, step by step, to the practical application of refracting instruments, as a means of directing and economising the light in a Pharos. This would involve the repetition, in a less elegant form, of what is to be found in all the works on optics; and instead of this, I am content to refer, where needful, to those works, and shall confine myself simply to what concerns Lighthouse lenses and their use. It would also be superfluous to determine the position of the principal focus of a plano-convex lens, in terms of the refractive index and radius of curvature,[55] as it can be very accurately found in practice by exposing the instrument to the sun, in such a manner that his rays may fall upon it in a direction parallel to its axis. The point of union between the converging and diverging cones of rays (where the spectrum is smallest and brightest), which is the principal focus, is easily found by moving a screen behind the lens, farther from or nearer to it as may be required. The path of the Lighthouse optician, moreover, generally lies in the opposite direction; and his duty is not so much to find the focal distance of a ready-made lens, as to find the best form of a lens for the various circumstances of a particular Pharos, whose diameter, in some measure, determines the focal distance of the instruments to be employed. All, however, that I shall really have to do is to give an account of what has been done by the late illustrious Fresnel, who seems to have devoted such minute attention to every detail[248] of the Dioptric apparatus, that he has foreseen and provided for every case that occurs in the practice of Lighthouse illumination. His brother, Mons. Leonor Fresnel, who succeeded him in the charge of the Lighthouses of France, has, with the greatest liberality, put me in possession of the various formulæ used by his lamented predecessor, in determining the elements of those instruments which have so greatly improved the lighthouses of modern days.
[55] F = rm - 1 in which r is the radius of curvature, and m is the refractive index.—Coddington’s Optics, Chap. VIII. If the radiant be brought near the lens, so as to cast divergent rays on its surface, then the conjugate focus will recede behind the principal focus; and when the luminous body reaches the principal focus in front of the lens, the rays will emerge from its posterior surface in a direction parallel to its axis. If it be brought still nearer the lens, the rays would emerge as a divergent cone. Hence converging lenses can only collect rays into a focus, when they proceed from some point more distant than the principal focus.
Spherical lenses, like spherical mirrors, collect truly into the focus those rays only which are incident near the axis; and it is, therefore, of the greatest importance to employ only a small segment of any sphere as a lens. The experience of this fact, among other considerations, led Condorcet, as already noticed, to suggest the building of lenses in separate pieces. Fresnel, however, was the first who actually constructed a lens on that principle; and he has subdivided, with such judgment, the surface of the lens into a centre lens and concentric annular bands and has so carefully determined the elements of curvature for each, that no farther improvement is likely to be made in their construction. For the drawings of the great lens, I have to refer to Plate XII., which also contains a tabular view of the elements of its various parts. The central disc of the lens, which is employed in lights of the first order, and whose focal distance is 920 millimètres, or 36·22 inches, is about 11 inches in diameter; and the annular rings which surround it vary slightly in breadth from 2³⁄₄ to 1¹⁄₄ inches. The breadth of any zone or ring is, within certain limits, a matter of choice, it being desirable, however, that no part of the lens should be much thicker than the rest, as well for the purpose of avoiding inconvenient projections on its surface, as to permit the rays to pass through the whole of the lens with nearly equal loss by absorption. The objects to be attained in the polyzonal or compound lens, are chiefly, as above noticed, to correct the excessive aberration produced by refraction through a hemisphere or great segment, whose edge would make the parallel rays falling on its curve surface converge to a point much nearer the lens than the principal focus, as determined for rays near the[249] optical axis, and to avoid the increase of material, which would not only add to the weight of the instrument and the expense of its construction, but would greatly diminish by absorption the amount of transmitted light. Various modes of removing similar inconveniences in telescopic lenses have been devised; and the suggestions of Descartes, as to combinations of hyperbolic and elliptic surfaces with plane and spherical ones, more especially fulfil the whole conditions of the case; but the excessive difficulty which must attend grinding and polishing those surfaces, has hitherto deprived us of the advantages which would result from the use of telescopic lenses entirely free from spherical aberration. In Lighthouse lenses, where so near an approach to accurate convergence to a single focus is unnecessary, every purpose is answered by the partial correction of aberration which may be obtained, by determining an average radius of curvature for the central disc, and for each successive belt or ring, as you recede from the vertex of the lens. In the lenses originally constructed for Fresnel by Soleil, the zones were united by means of small dowels or joggles of copper, passing from the one zone into the other; but the greater exactness of the workmanship now attained, has rendered it safe to dispense with those fixtures; and the compound lens is now held together solely by a metallic frame and the close union between the concentric faces of the rings, which, however, are in contact with each other at surfaces of only ¹⁄₄ inch in depth, as shewn in Plate XII. It is remarkable, that an instrument, having about 1300 square inches of surface, and weighing 109 lb., and which is composed of so many parts, should be held together by so slender a bond as two narrow strips of polished glass, united by a thin film of cement.
I now proceed to the formulæ employed by Fresnel, to determine the elements of the compound lens,[56] in the calculation of[250] which two cases occur, viz., the central disc and a concentric ring. The focal distance of the lens and the refractive index of the glass are the principal data from which we start.
[56] It may be proper to mention that, while the formulæ given in the text are those of M. Fresnel, I am responsible for the investigations in the Notes; I have, at the same time, much pleasure in acknowledging my obligations, at various times (about ten years ago), to Mr Edward Sang, and (more recently) to Mr William Swan, for their kind advice on this part of the subject.
Fig. 54.
I begin with the case of the central disc or lens round which the annular rings are arranged. Its principal section is a mixtilinear figure (fig. 54) composed of a segment b a c, resting on a parallelogram b c d e, whose depth b d or c e is determined by the strength which is required for the joints which unite the various portions of the lens. Those particulars have, as I already stated, been determined with so much judgment by Fresnel and the dimensions of the lenses so varied to suit the case of various lights, that nothing in this respect remains to be done by others.
Fig. 55.
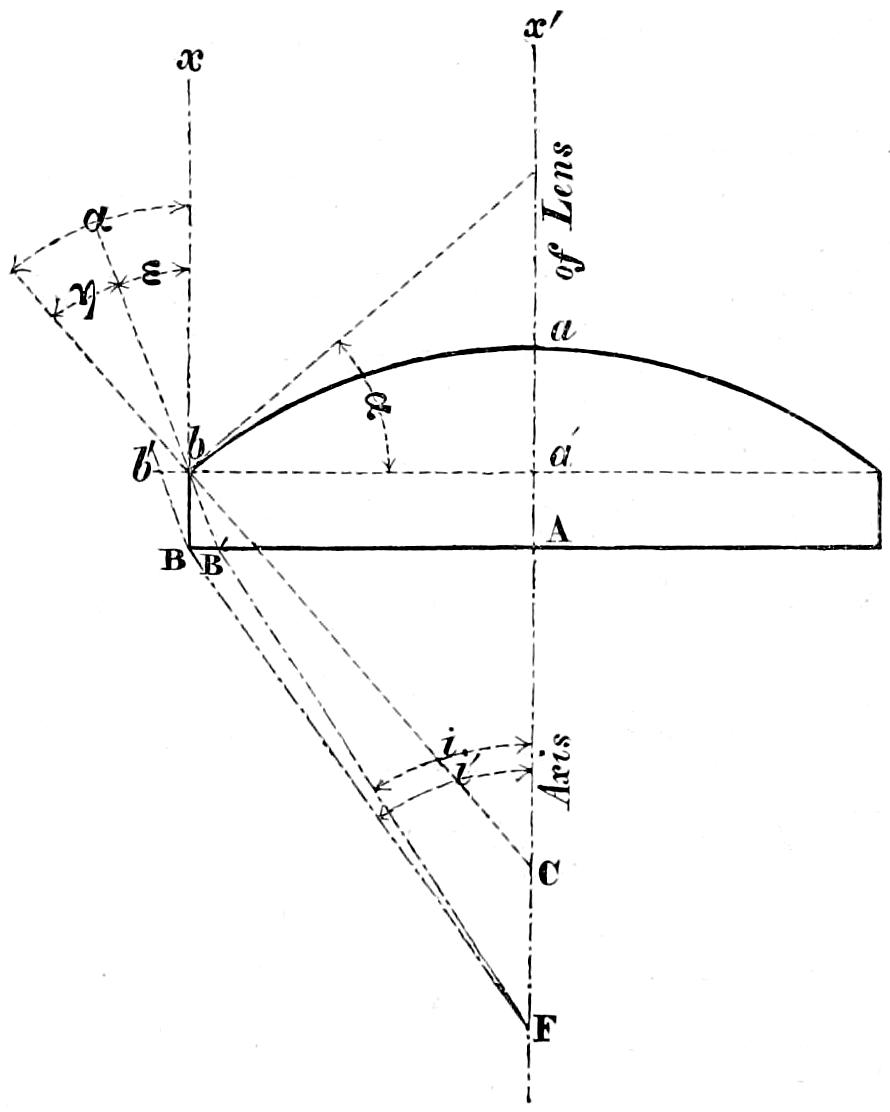
Referring to fig. 55, we have, for obtaining the radius of the central disc, the following formulæ, in which
r = AB, half the aperture of the lens
r′ = AB′
φ = AF, the focal distance
t′ = A a, the thickness of the lens at the vertex
t″ = B b, the thickness of the joint
μ = the index of refraction
ρ = the radius of curvature.
Then for the radius of curvature near the axis we have:
ρ′ = (μ - 1)(φ + t′μ)
and for that near the margin we have:
[251]
tan i′ = rφ
sin e = sin i′μ
r′ = r - t″ . tan e
tan i = r′φ
sin ε = sin iμ
ρ″ = rμ sin e √μ² - 2 μ cos e + 1
and, finally ρ = ρ′ + ρ″ 2[57]
[57] The following steps lead to the formulæ given in the text. Let APQB (fig. 56) represent a section of the central lens by a plane passing through its axis AF; F the focus for incident rays; and FQPH the path of a ray refracted finally in the direction PH, parallel to the axis. Let C be the centre of curvature, then PC is a normal to the curve at P; and, producing PQ to meet the axis in G, we have G the focus of the rays, after refraction at the surface BQ.
Fig. 56.
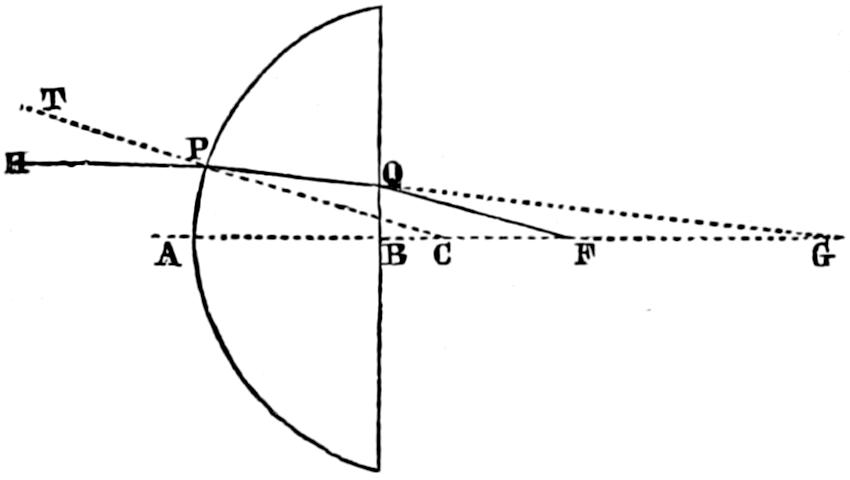
Then μ = sin PCGsin GPC = PGCG; and also μ = sin QFGsin QGF = QGQF
Now, as P approaches A, we have ultimately PG = AG, QG = BG, and QF = BF;
Therefore, putting AG = θ and AC = ρ′
μ = AGCG = θθ - ρ′; μ = BGBF = θ - t′φ,
from which μ θ - μ ρ′ = θ; and μ φ = θ - t′ and eliminating θ, we have μ² φ + μ ρ′ = μ φ + t′, whence, as above, ρ′ = (μ - 1)(φ + t′μ.)
But as this value of the radius of curvature, as already stated, is calculated for rays near the axis, it would produce a notable aberration for rays incident on the margin of the lens. In order, therefore, to avoid the effects of aberration as much as possible, a second radius of curvature must be calculated, so that rays incident on the margin of the lens may be refracted in a direction parallel to the axis. This second value of the radius is called ρ″ in the text, and is found as follows (referring to fig. 57):
Let FB′ b x be the course of a ray refracted in the direction b x parallel to the axis A x′. This ray meets the surface AB in the point B′, whose position may be found approximately by tracing the path of the ray FB, on the supposition that the surface of the refracting medium is produced in the directions AB, a′ b′.
Fig. 57.
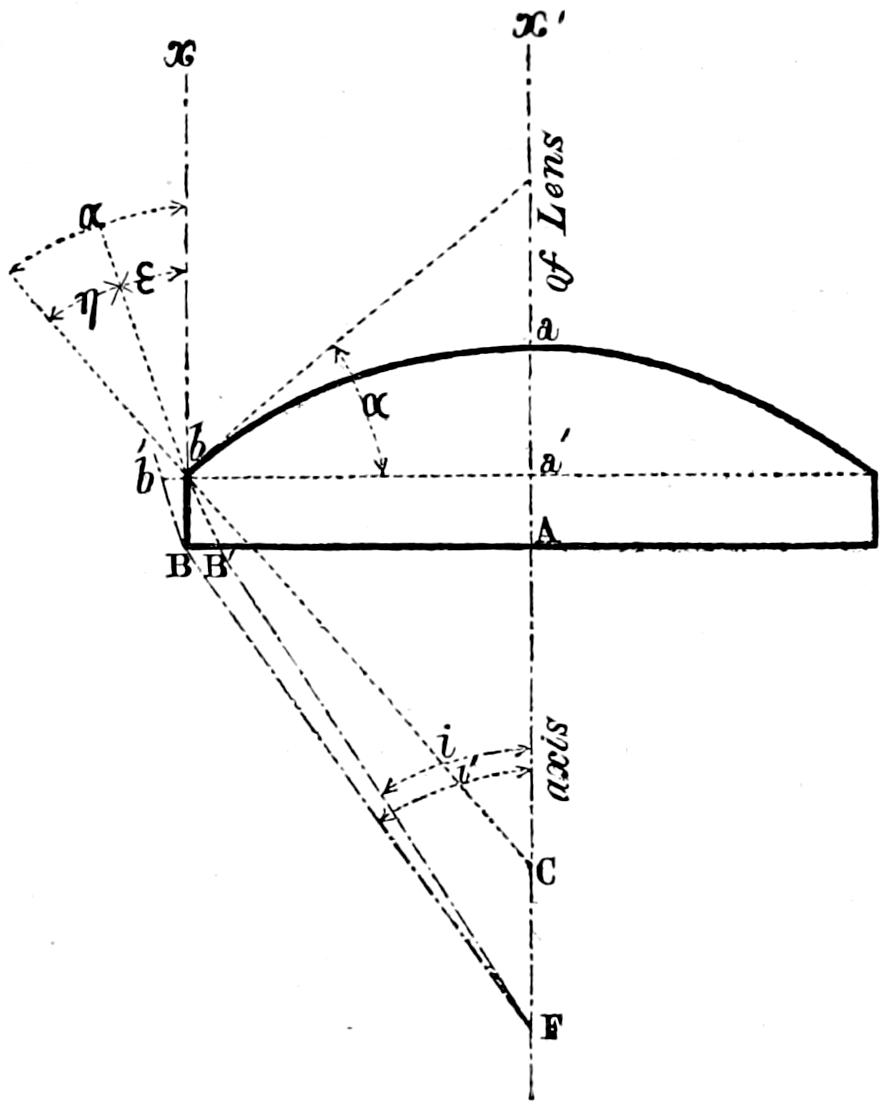
Let C be the centre of curvature (see fig. 57)
α = AC b the angle of emergence
η = B′ b C the second angle of refraction
ε = B b B′ the first angle of refraction
i = B′FA the first angle of incidence
i′ = BFA
e = b′ B b
AB = r
AB′ = r′
B b = t″ the thickness of the lens at the edge
AF = φ the focal distance.
Then tan i′ = rφ; sin e = sin i′μ whence b b′ = t″ tan e becomes known.
Now, since BB′ = b b′ nearly, AB′ = AB - b b′ or r′ = r - t″ tan e.
From this is obtained the angle of incidence i, and the first angle of refraction ε; for tan i = r′φ and sin ε = sin iμ.
| Next B′ b C = B b C - B b B′ or η = α - ε and sin α = μ sin η = μ sin (α - ε) |
| from which, sin α cos ε - cos α sin ε = sin α μ |
| whence sin α (cos ε - 1 μ) = cos α sin ε; and |
| sin² α (cos² ε - 2 cos εμ + 1μ²) = cos² α sin² ε = (1 - sin² α) sin² ε = sin² ε - sin² α sin² ε |
Then transposing we have
sin² α {(cos² ε + sin² ε) - 2 cos εμ + 1μ²} = sin² ε
and because (cos² ε + sin² ε) = 1 we have, by dividing,
sin² α = sin² ε {1 - 2 cos εμ + 1μ²} = μ² sin² ε μ² - 2 μ cos ε + 1
and sin α = μ sin ε √1 - 2 μ cos ε + μ²
Next, since b C = a′ b
sin AC b
= rsin α,
putting C b = ρ″, and substituting
we have ρ″ = rμ sin ε
√μ² - 2 μ cos ε + 1
and, taking for the radius of curvature, the mean of ρ′ and ρ″ the values calculated for the
central and marginal rays, we have finally ρ = ρ′ + ρ″
2
Fig. 58.
I come next to the second case, which concerns the calculation of the elements of a concentric ring. The section a b c d e (fig. 58) of one of those rings includes a mixtilinear triangle a b e, and a rectangle b c e d, the thickness b c being the same as that of the edge of the central disc; and the elements to be determined are the radius of the curve surface, and the position of the centre of curvature, with reference to the vertex of the lens.
Fig. 59.
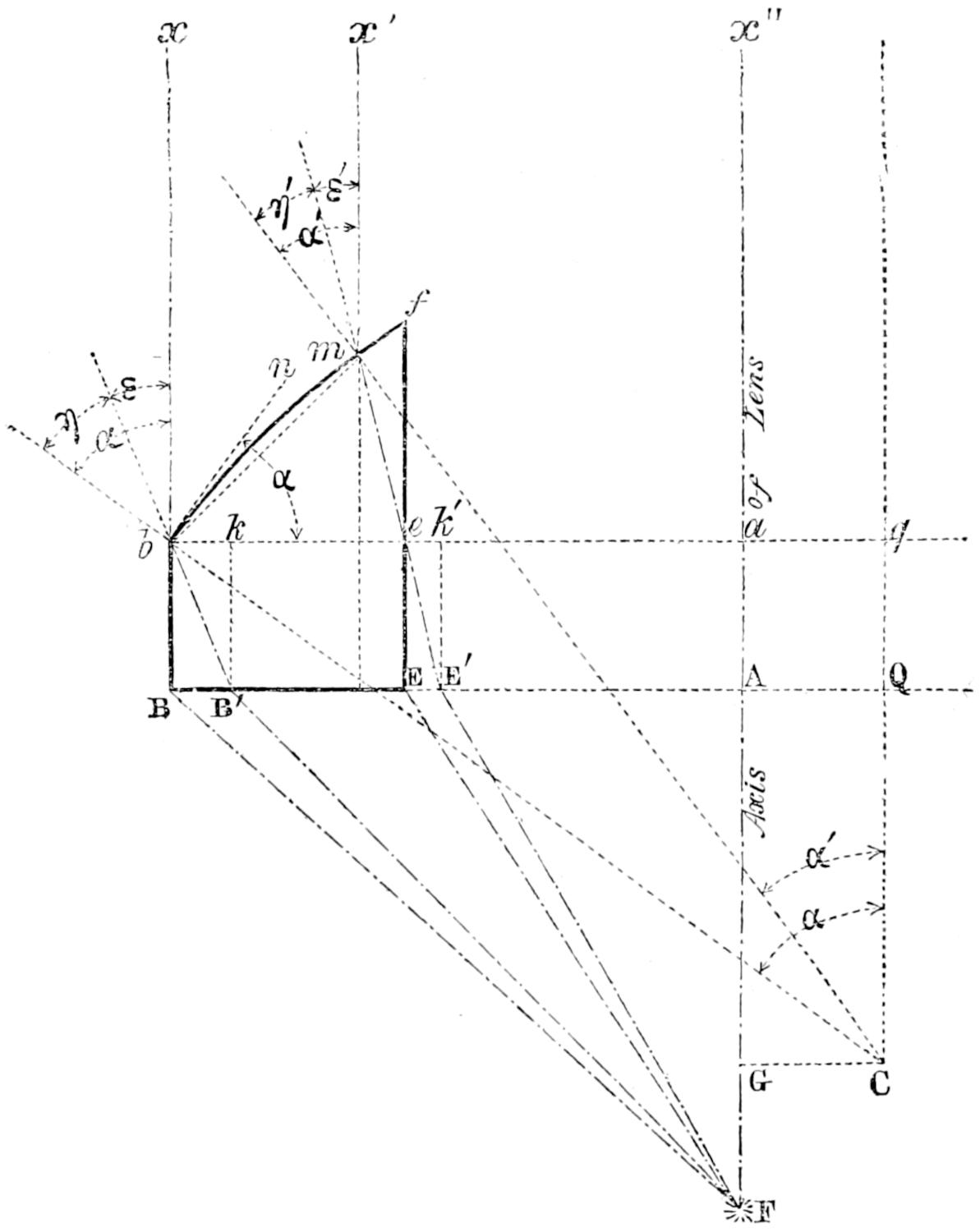
The radius of curvature of the zone may be calculated by the following formulæ, in which (see fig. 59)
r₁ = AB the distance of the outer margin of the zone from the axis of the lens
r₂ = AE the distance of the inner margin from the axis
l = BE the breadth of the zone = r₁ - r₂
ρ = the radius of curvature = b C = m C
φ = focal distance AF
t = thickness of the joint B b
t″ = B b
μ = refractive index of the glass
i₁ = BFA
i₂ = EFA
Then tan i′₁ = r₁φ; tan i′₂ = r₂φ
sin e₁ = sin i′₁μ; sin e₂ = sin i′₂μ
r′₁ = r₁ - t″ sin e₁; r′₂ = r₂ - t″ sin e₂
tan i₁ = r′₁φ; tan i₂ = r′₂φ
sin ε = sin i₁μ; sin ε′ = sin i₂μ
sin α = μ sin ε √μ² - 2 μ cos ε + 1;
sin α′ = μ sin ε′ √μ² - 2 μ cos ε′ + 1; η = α′ - ε′
and lastly ρ = 2 cos ε′ 2 cos {η + ¹⁄₂(α - α′)} sin ¹⁄₂ (α - α′)
which is Fresnel’s value of the radius of curvature.[58]
[58] The following steps will conduct us to this expression:
Fig. 60.
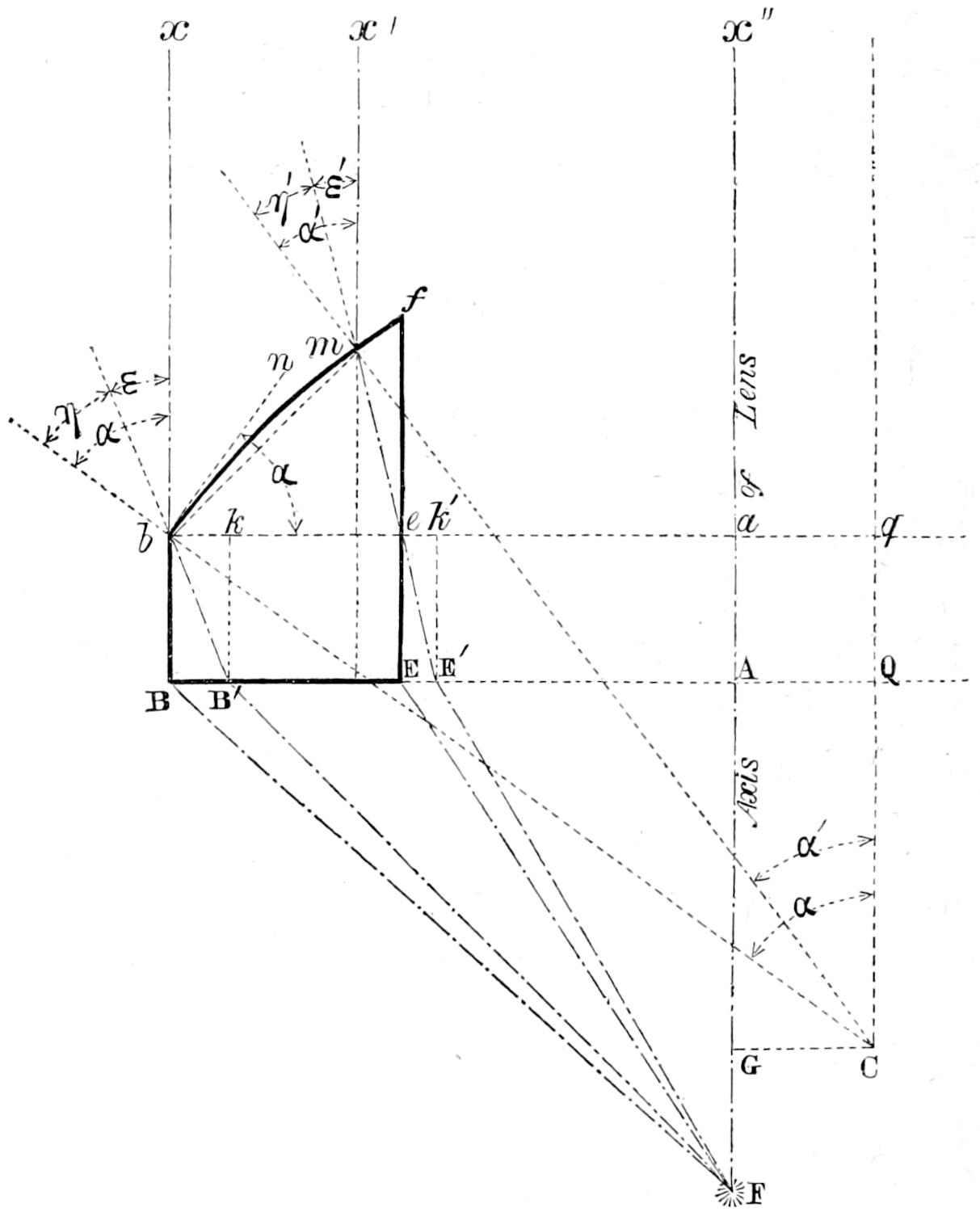
Let B b f E (fig. 60) represent the section of a zone by a plane passing through the axis of the lens AF, C the centre of curvature, F the radiant point, and FB′ b x, FE′m x′ the course of the extreme rays which are transmitted through the zone (and the latter of which passes from E′ to e through a portion of the zone or lens in contact with that under consideration). Then putting
AB = r₁; AB′ = r′₁; C b = ρ
AE = r₂; AE′ = r′₂; B b = t″; BE = r₁ - r₂ = l
ε = the first angle of refraction b B′ k
η = the second angle of refraction B′ b C
ε′ = the first angle of refraction e E k′
η′ = the second angle of refraction e m C
α = the angle of emergence b C q
α′ = the angle of emergence m C q
i′₁ = BFA; i′₂ = EFA; i₁ = B′FA; i₂ = E′FA
e₁ = B b B′; e₂ = E e E′.
Proceeding exactly as in the case of the central lens we shall have
tan i′₁ = BAAF = r₁φ; tan i′₂ = EAAF = r₂φ
sin e₁ = sin i′₁μ; sin e₂ = sin i′₂μ
r′₁ = r₁ - t″ sin e₁; r′₂ = r₂ - t″ sin e₂
tan i₁ = r′₁φ; tan i₂ = r′₂φ
sin ε = sin i₁μ; sin ε′ = sin i′₂μ
sin α = μ sin ε √μ² - 2 μ cos ε - 1; and sin α′ = μ sin ε′ √μ² - 2 μ cos ε′ + 1
Now, the angle b C m = α - α′ from which (since the triangle b m C is isosceles) b m C = 90° - ¹⁄₂ (α - α′); also, in the triangle b m e, the angle b m e = b m C - e m C = 90° - ¹⁄₂ (α - α′) - η and b e m = k′ e E′ = 90° - ε′
We have therefore in the triangle b m e
b m = b e sin b e m sin b m e = l cos ε′cos {η + ¹⁄₂ (α - α′)}
and in b m C
| b C | = | b m sin b m C sin b C m = l cos ε′ cos ¹⁄₂ (α - α′) (cos (η + ¹⁄₂ (α - α′)) sin (α - α′) |
| = l cos ε′ cos ¹⁄₂ (α - α′) cos {η + ¹⁄₂ (α - α′)} 2 sin ¹⁄₂ (α - α′) cos ¹⁄₂ (α - α′) | ||
from which, putting b C = ρ
ρ = l cos ε′ 2 cos {η + ¹⁄₂ (α - α′)} sin ¹⁄₂ (α - α′)
[254]
Lastly, the position of C the centre of curvature for a ring is easily determined by two co-ordinates in reference to their origin, A, which is the vertex of the lens (see fig. 60 below), by the equations:
| CG | = | ρ . sin α - a b | = | ρ . sin α - r₁ |
| CQ | = | ρ . cos α - q Q | = | ρ . cos α - t″ |
[255]
The elements of each successive zone are determined in the same manner. The annular lens of the first order of lights in Fresnel’s system consists, as already stated, of a central disc 11 inches in diameter, and 10 concentric rings, all of which have a common principal focus, where the rays of the sun meet after passing through the lens. With such accuracy are those rings and the disc ground and placed relatively to each other, that the position of the actual conjugate focus of the entire surface of the compound lens, differs in a very small degree from that obtained by calculation in the manner described below.[59]
Testing Lenses. The tests generally applied for examining the lenses used in Lighthouses, is to find the position of the conjugate focus behind the lens, due to a given position of a lamp in front of it. This test depends on the following considerations:—Draw a line from an object O in front of a lens, to any point Q in the lens; and from A, the centre of the lens, draw AR parallel to OQ, and cutting a line RF r which passes through the principal focus F, at right angles to the axis of the lens; then join the points Q and R, and produce the line joining them: I, the image of O must be in that line. In the same way, draw a line from O to q, another point in the lens on the other side of its axis, and parallel to it draw A r from the centre of the lens, cutting the plane of the principal focus in r. Join q r, in which line the image will lie; and hence the intersection of OR and q r, in I, will be the point in which the image of O is formed, or will be the conjugate focus of the lens due to the distance OA. This mode will serve to give the distance of the conjugate focus of a lens (neglecting its thickness) for rays falling on its surface at any angle.
Fig. 61.
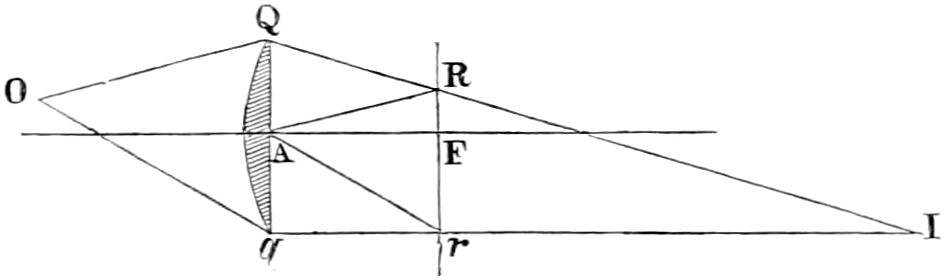
We shall suppose QA (fig. 61) to represent the half of a lens, and remembering the conditions described in reference to the last figure, we shall at once perceive the truth of the following analogy (fig. 62):—
Fig. 62.

OA ∶ AF ∷ AQ ∶ FR ∷ AI ∶ FI, and putting OA = δ, AI = φ′, and AF = φ, we have δ ∶ φ ∷ φ′ ∶ φ′ - φ, and, consequently, δ φ′ - δ φ = φ φ′; and hence the following equations, which express the relations subsisting between the principal focus of the lens and the distance of any object and its corresponding image:
1st, To find the principal focal distance of a lens from the measured position of its object and its image refracted through it, we have, φ = δ φ′ δ + φ′.
2d, For the distance of the object, when that of the image is known, we have, δ = φ φ′φ′ - φ.
3d, For the position of the image, when that of the object is known, we have, φ′ = δ φδ - φ.
Fig. 63.
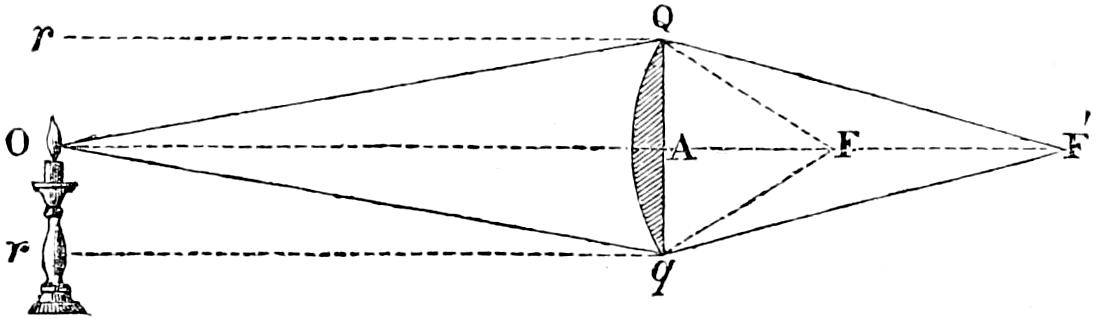
In testing lenses, of course, it is this last equation which we use, because the value of φ or the principal focus is always known, and is that whose accuracy we wish to try, while δ may be chosen within certain limits at will. I have found that the best mode of proceeding is the following:—In front of the lens Q q (see fig. 63) firmly fixed on a frame, place a lamp at O at the distance of about 50 yards. Calculate the value of φ′ due to 50 yards, which in this case is equal to AF′, OA being equal to δ; and move a screen of white paper backwards and forwards until you receive on it the smallest image that can be formed, which is at the point where the cones of converging and diverging rays meet. The image will always increase in size whether you approach nearer to the lens or recede farther from it, according as you pass from the converging into the diverging cone of rays, or vice versa; and hence the intermediate point is easily found by a very little practice. The distance from the centre of the lens to the face of the screen, which must be adjusted so as to be at right angles to a line joining the centre of the lens and the lamp, is then measured; and its agreement with the calculated length of φ′, is an indication of the accuracy of the workmanship of the lens. When the measured distance is greater than the calculated φ′, we know that the lens is too flat; and it is on this side the error generally falls. On the other hand, when φ′ is greater than the measured distance, we know that the lens has too great convexity. I have only to add, that an error of ¹⁄₆₀ on the value of φ′ may be safely admitted in Lighthouse lenses; but I have had many instruments made by M. François Soleil, whose error fell below ¹⁄₈₀ of φ′. Owing probably to the mode of grinding, the surfaces of all the lenses I have yet examined are somewhat too flat.
In the combination of lenses with the flame of a lamp, similar considerations must influence us in making the necessary arrangements, as in the case of reflectors. We have already seen that the size of the flame and its distance from the surface of reflecting instruments have an important practical bearing on the utility of the instrument, Divergence of Annular Lenses. and that the divergence of the resultant beam materially affects its fitness for the purpose of a Lighthouse. So also, in the case of the lens, unless the diameter of the flame of the lamp has to the focal distance of the instrument a relation such as may cause an appreciable divergence of the rays refracted through it, it could not be usefully applied to a Lighthouse; for, without this, the light would be in sight during so short a time, that the seaman would have much difficulty in observing it. To determine the amount of this divergence of the refracted beam, therefore, is a matter of great practical importance, and I shall briefly point out the conditions which regulate its amount, as they are nearly identical with those which determine the divergence of a paraboloïdal mirror illuminated by a lamp in its focus. The divergence, in the case of lenses, may be described as the angle which the flame subtends at the principal focus of the lens, the maximum of which, produced at the vertex of Fresnel’s great lens by the lamp of four concentric wicks, is about 5° 9′.[60]
[60] This will be easily seen by examining the annexed figure (64), in which Q q represents the lens. A its centre, F the principal focus, b F and b′ F the radius of the flame; then is the angle b A b′ equal to the maximum divergence of the lens. Sin b AF = b FAF = sin b′ AF = Rad. of flameFocal distance; and twice b AF = the whole divergence at A. Then for the divergence at the margin of the lens, or at any other point, we have, FQ = √AQ² + AF² and Q x = √QF² + F x²; and for any angle at Q, we have sin FQ x = F xFQ.
Fig. 64.
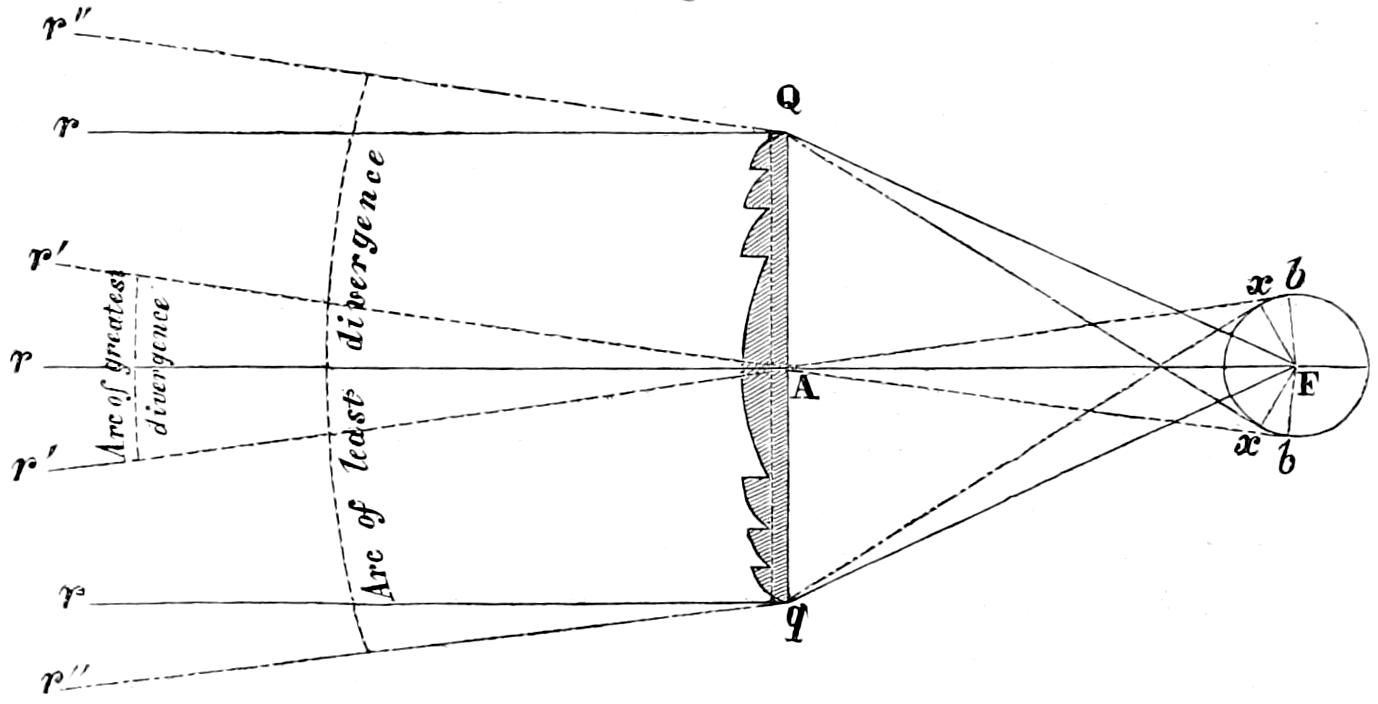
Illuminating Power of Lenses. On the subject of the illuminating power of the lenses, it seems enough to say, that the same general principle regulates the estimate as in reflectors. Owing to the square form of the lens, however, there is a greater difficulty in finding a mean focal distance whereby to correct our estimate of the angle subtended by the light, so as to equate the varying distance of the several parts of the surface; but, practically, we shall not greatly err if we consider the quotient of the surface of the lens divided by the surface of the flame as the increased power of illumination by the use of the lens. The illuminating effect of the great lens, as measured at moderate distances,[258] has generally been taken at 3000 Argand flames, the value of the great flame in its focus being about 16, thus giving its increasing power as nearly equal to 180. The more perfect lenses have produced a considerably greater effect.
The application of lenses to Lighthouses is so obvious as scarcely to admit of farther explanation than simply to state, Arrangement of the Lenses in a Lighthouse. that those instruments are arranged round a lamp placed in their centre, and on the level of the focal plane in the manner shewn in Plates XIII. and XIV.,[61] so as to form by their union a right octagonal hollow prism, circulating round the flame which is fixed in the centre, and shewing to a distant observer successive flashes or blazes of light, whenever they cross a line joining his eye and the[259] lamp, in a manner similar to that already noticed in describing the action of the mirrors. The chief difference in the effect consists in the greater intensity and shorter duration of the blaze produced by the lens; which latter quantity is, of course, proportional to the divergence of the resultant beam. Each lens subtends a central horizontal pyramid of light of about 46° of inclination, beyond which limits the lenticular action could not be advantageously pushed, owing to the extreme obliquity of the incidence of light; but Fresnel at once conceived the idea of pressing into the service of the mariner, by means of two very simple expedients, the light which would otherwise have uselessly escaped above and below the lenses.
[61] The Plates shew the nature of the mechanical power which gives movement to the lenses. It consists of a clockwork movement driven by a weight which sets in motion a plate bearing brackets that carry the lenses. All this, however, can be seen from the Plates; and I am unwilling to expend time in a detailed explanation of what is obvious by inspection.
For intercepting the upper portion of the light, Fresnel employed eight smaller lenses of 500 mm. focal distance (19·68 inches) inclined inwards towards the lamp, which is also their common focus and thus forming, by their union, Pyramidal Lenses and Mirrors. a frustum of a hollow octagonal pyramid of 50° of inclination. The light falling on those lenses is formed into eight beams parallel to the axis of the smaller lenses, and rising upwards at an angle of 50° inclination. Above them are ranged eight plane mirrors, so inclined (see Plates XIII. and XIV.) as to project the beams transmitted by the small lenses in the horizontal direction, so as finally to increase the effect of the light. In placing those upper lenses, it is generally thought advisable to give their axis an horizontal deviation of 7° or 8° from that of the great lenses and in the direction contrary to that of the revolution of the frame which carries the lenticular apparatus. By this arrangement, the flashes of the smaller lenses precede that of the large ones, and thus tend to correct the chief practical defect of revolving lenticular lights by prolonging the bright periods. The elements of the subsidiary lenses depend upon the very same principles, and are calculated by the same formulæ as those given for the great lenses. In fixing the focal distance and inclination of those subsidiary lenses, Fresnel was guided by a consideration[260] of the necessity for keeping them sufficiently high to prevent interference with the free access to the lamp. He also restricted their dimensions within very moderate limits, so as to avoid too great weight. The focal distance is the same as that for lenses of the third order of lights.
Fig. 65.
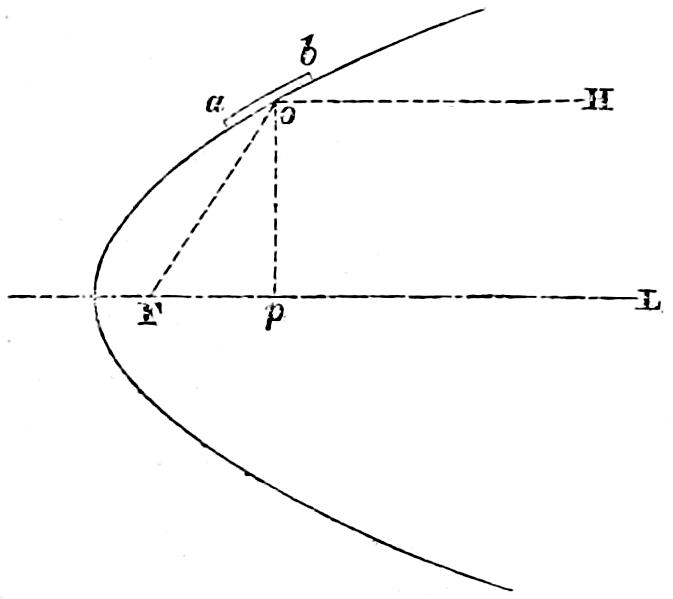
Owing to the necessary arrangements of a lantern, only a very small portion of those rays, which escape from below the lenses, can be rendered available for the purposes of a Lighthouse; and any attempt to subject it to lenticular action, so as to add it to the periodic flashes, would have led to a most inconvenient complication of the apparatus. Fresnel adopted the more natural and simple course of transmitting it to the horizon in the form of flat rings of light, or rather of divergent pencils, directed to various points of the horizon. Curved Mirrors. This he effected by means of small curved mirrors, disposed in tiers, one above another, like the leaves of a Venetian blind—an arrangement which he also adopted (shewn in Plates XV. and XVI.) for intercepting the light which escapes above as well as below the dioptric belt in fixed lights. Those curved mirrors are, strictly speaking, generated (see fig. 65) by portions, such as a b, of parabolas, having their foci coincident with F, the common flame of the system. In practice, however, they are formed as portions of a curved surface, ground by the radius of the circle, which osculates the given parabolic segment.[62] The mirrors are plates of glass, silvered on the back and set in flat cases of sheet-brass. They are suspended on a circular frame by[261] screws, which are attached to the backs of the brass cases, and which afford the means of adjusting them to their true inclination, so that they may reflect objects on the horizon of the Lighthouse[262] to an observer’s eye, placed in the common focus of the system.[63]
[62] To find the radius and centre of a circle, which shall osculate a given parabola, whose focus is in F, draw the normals to the curve from p and P, meeting in O, and draw N e parallel to a tangent of the curve, or to p P, then P O or p O is the radius required. Now, we have similar triangles P p d and N e n, and P H and p h are (proximate) ordinates; hence we have the following analogies:—
P d ∶ P p ∷ PH ∶ PN
N e ∶ N n ∷ PH ∶ PN
Fig. 66.
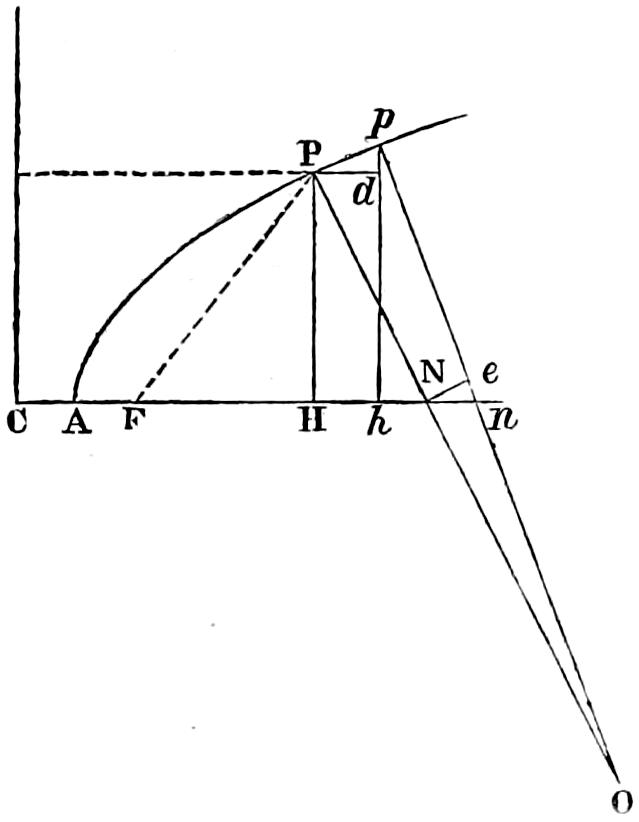
Hence compounding those ratios (in which P d = N n nearly)
| N e ∶ P p | ∷ | PH² ∶ PN² |
| also N e ∶ P p | ∷ | NO ∶ PO, |
(for O P p and N o e are similar triangles)
| PH² ∶ PN² ∷ NO ∶ OP, | |
| then PN²- PH² = HN² | |
| and PO - NO = NP, | |
| therefore | HN² ∶ PN² ∷ NP ∶ PO, |
| and finally, PO = PN³ HN². |
| Then put FP = HC = FN = ρ; HN | = | ρ - z; then as FP² - FH² = PH² = ρ² - z² |
| PN² = PH² + HN² | = | (ρ² - z²) + (ρ² - 2 ρ z + z²) |
| = | 2ρ² - 2 ρ z | |
| PN | = | √2 ρ (ρ - z) |
| Therefore PO | = | √{2 ρ (ρ - z)}³ (ρ - z)² |
| = | √{2 ρ (ρ - z)}³ (ρ - z)⁴ | |
| and finally, PO | = | 2√2 √ρ³ ρ - z |
Fig. 67.
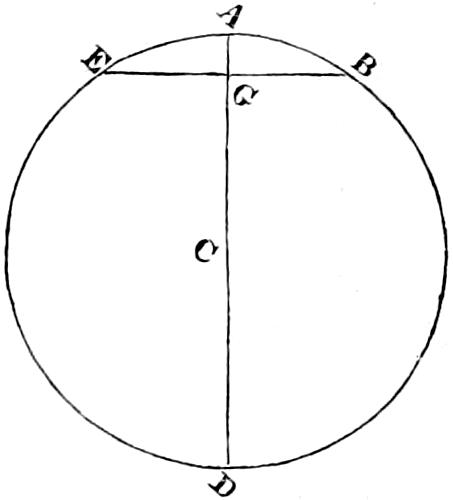
To find the versed sine of the curvature (which may be useful in the examination of the mirrors by a mould) we may proceed (see fig. 67) to
put AG = f; BE = C; AC = R
then BG² = AG . GD
4 BG² = BE² = 4 AG . GD
C² = 4 f . (2 R - f)
C² = 8 f R - 4 f²
From which equation,
2 f - 2 R = ± √4 R² - C² = -2 R +
C²4 R -
C⁴64 R³ &c.
2 f = C²4 R -
C⁴64 R³
f = C²8 R -
C⁴128 R³.
Fig. 68.
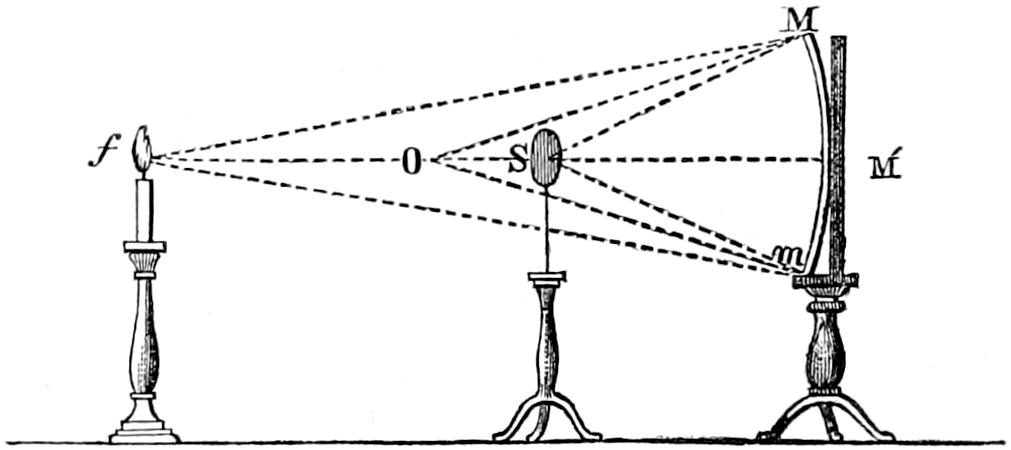
In order to test the accuracy of the workmanship of the mirrors, recourse must again be had, as in the case of the lenses and parabolic mirrors, to the formula of conjugate foci, in which we shall call R = the radius of curvature of the mirror M m (fig. 68); a = the distance of a light, f, which is arbitrarily placed in front of the mirror; and b = the distance of a moveable screen S, on which the rays reflected from the mirror may converge in a focus. We must find the distance b, at which, with any given distance a, such convergence should take place.
f M′ = a
SM′ = b
OM′ = R
Then (because f MS is bisected by OM, and for points near the vertex of the mirror at M′)
| SM′ ∶ f M′ ∷ SO ∶ O f | |
| or | b ∶ a ∷ R - b ∶ a - R |
| a b - R a = R b - a b. |
From which b = R a 2 a - R, the distance required, in which an error of ¹⁄₃₀ (of its whole length) may be safely admitted.
[63] At such times when the horizon cannot be seen, the mirror may be placed, by means of a clinometer, with a spirit-level, set to the proper angle, which may be easily mechanically determined as follows: Draw a line from the focus F through the point O, where the centre of the mirror is to be, producing it beyond that point to a convenient distance at I; through O draw HOH, parallel to the horizon FH; bisect IOH by MOM, which coincides with a tangent to the mirror at its centre O; and MOH is the angle required to be laid off, or its complement.
Fig. 69.
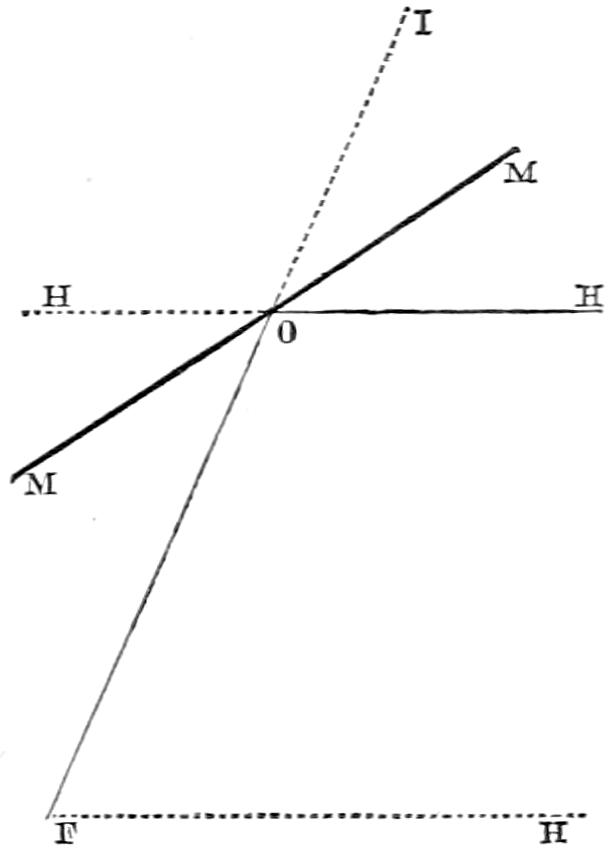
[263]
Cylindric Refractors for Fixed Lights. Having once contemplated the possibility of illuminating Lighthouses by dioptric means, Fresnel quickly perceived the advantage of employing for fixed lights a lamp placed in the centre of a polygonal hoop, consisting of a series of refractors, infinitely small in their length and having their axes in planes parallel to the horizon. Such a continuation of vertical sections, by refracting the rays proceeding from the focus, only in the vertical direction, must distribute a zone of light equally brilliant in every point of the horizon. This effect will be easily understood, by considering the middle vertical section of one of the great annular lenses, already described, abstractly from its relation to the rest of the instrument. It will readily be perceived that this section possesses the property of simply refracting the rays in one plane coincident with the line of the section and in a direction parallel to the horizon, and cannot collect the rays from either side of the vertical line; and if this section, by its revolution about a vertical axis, becomes the generating line of the enveloping hoop, above noticed, such a hoop will of course possess the property of refracting an equally diffused zone of light round the horizon. The difficulty, however, of forming this apparatus appeared so great, that Fresnel determined to substitute for it a vertical polygon, composed[264] of what have been improperly called cylindric lenses, but which in reality are mixtilinear and horizontal prisms, distributing the light which they receive from the focus nearly equally over the horizontal sector which they subtend. This polygon has a sufficient number of sides to enable it to give, at the angle formed by the junction of two of them, a light not very much inferior to what is produced by one of the sides; and the upper and lower courses of curved mirrors are always so placed as partly to make up for the deficiency of the light at the angles. The effect sought for in a fixed light is thus obtained in a much more perfect manner, than by any combination of the parabolic mirrors used in the British Lighthouses.
Application of crossed prisms to cause occasional flashes.An ingenious modification of the fixed apparatus is also due to the inventive mind of Fresnel, who conceived the idea of placing one apparatus of this kind in front of another, with the axis of the cylindric pieces crossing each other at right angles. As those cylindric pieces have the property of refracting all the rays which they receive from the focus, in a direction perpendicular to the mixtilinear section which generates them, it is obvious that if two refracting media of this sort be arranged as above described, their joint action will unite the rays which come from their common focus into a beam, whose sectional area is equal to the overlapped surface of the two instruments, and that they will thus produce, although in a disadvantageous manner, the effect of an annular lens. It was by availing himself of this property of crossed prisms, that Fresnel invented the distinction for lights, which he calls a fixed light varied by flashes; in which the flashes are caused by the revolution of cylindric refractors with vertical axes, ranged round the outside of the fixed light apparatus already described.
Having been directed by the Commissioners of the Northern Lighthouses to convert the fixed catoptric light of the Isle of May, into a dioptric light of the first order, I proposed, that an attempt should be made True Cylindric form given to the Refractors and other improvements in their Construction. to form a true cylindric, instead of a polygonal belt for the refracting part of the apparatus; and this task was successfully[265] completed by Messrs Cookson of Newcastle in the year 1836. The disadvantage of the polygon lies in the excess of the radius of the circumscribing circle over that of the inscribed circle, which occasions an unequal distribution of light between its angles and the centre of each of its sides; and this fault can only be fully remedied by constructing a cylindric belt, whose generating line is the middle mixtilinear section of an annular lens, revolving about a vertical axis passing through its principal focus. This is, in fact, the only form which can possibly produce an equal diffusion of the incident light over every part of the horizon.
I at first imagined that the whole hoop of refractors might be built between two metallic rings, connecting them to each other solely by the means employed in cementing the pieces of the annular lenses; but a little consideration convinced me that this construction would make it necessary to build the zone at the lighthouse itself, and would thus greatly increase the risk of fracture. I was therefore reluctantly induced to divide the whole cylinder into ten arcs, each of which being set in a metallic frame, might be capable of being moved separately. The chance of any error in the figure of the instrument has thus a probability of being confined within narrower limits; whilst the rectification of any defective part becomes at the same time more easy. One other variation from the mode of construction at first contemplated for the Isle of May refractors, was forced upon me by the repeated failures which occurred in attempting to form the middle zone in one piece; and it was at length found necessary to divide this belt by a line passing through the horizontal plane of the focus. Such a division of the central zone, however, was not attended with any appreciable loss of light, as the entire coincidence of the junction of the two pieces with the horizontal plane of the focus, confines the interception of the light to the fine joint at which they are cemented. With the exception of those trifling changes, the idea at first entertained of the construction of the instrument was fully realised at the manufactory of Messrs Cookson. I also, at a subsequent period, greatly[266] improved the arrangement of this apparatus, by giving to the metallic frames which contain the prisms, a rhomboidal,[64] instead of a rectangular form. The junction of the frames being thus inclined from the perpendicular, do not in any azimuth intercept the light throughout the whole height of the refracting belt, but the interception is confined to a small rhomboidal space, whose area is inversely proportional to the sine of the angle of inclination; and if the helical joints be formed between the opposite angles of the old rectangular frames, the amount of intercepted light becomes absolutely equal in every azimuth.[65]
[64] The form would not be exactly rhomboidal, but would be a portion of a flat helix intercepted between two planes, cutting the enveloped cylinder at right angles to its axis.
[65] See my Report on the Refractors of the Isle of May Light, 8th October 1836.
Fig. 70.
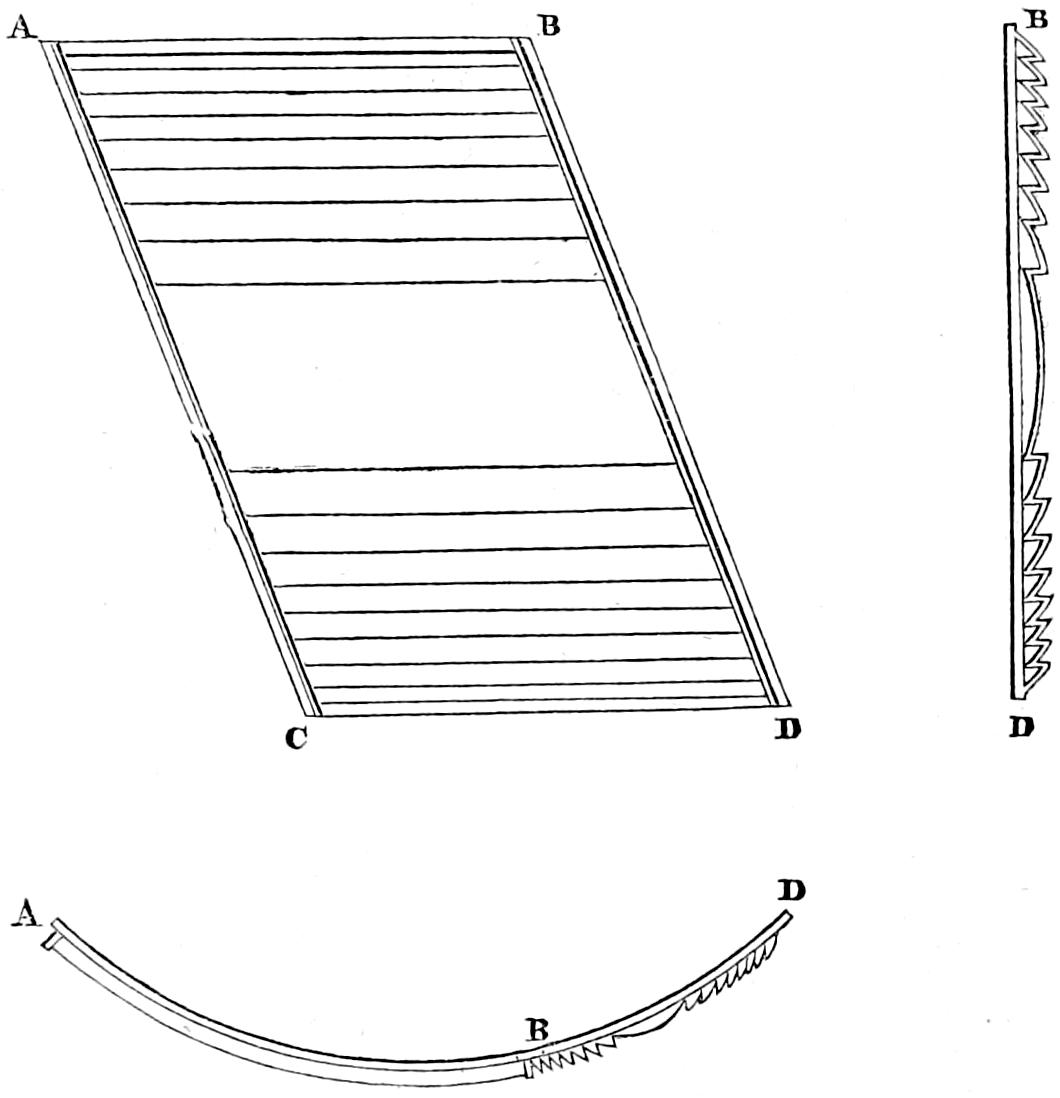
Such an apparatus is shewn in Plate XVII.; and the accompanying diagram (fig. 70) shews an elevation ABCD, a section BD, and a plan ABD, of a single pannel of this improved compound belt. AC and BD are the diagonal joints above described. Time and perseverance, and the patience and skill of Monsieur[267] François Soleil, whom I urged to undertake the task, were at length crowned with success; and I had the satisfaction at last of seeing a fixed light apparatus, having its form truly cylindric, and its central belt in one piece, while the joints were inclined to the horizon at such an angle as to render the light perfectly equal in every azimuth.
The loss of light by reflection at the surface of the most perfect mirrors, and the perishable nature of the material composing their polish, induced me, so far back as 1835, in a Report on the Light of Inchkeith, which had just been altered to the dioptric system, to propose the substitution of totally reflecting prisms, even in lights of the first order or largest dimensions. In this attempt I was much encouraged by the singular liberality of Mr Leonor Fresnel, to whose friendship (as I have often, with much pleasure, acknowledged) I owe all that I know of dioptric Lighthouses. He not only freely communicated to me the method pursued by his distinguished brother Augustin Fresnel, in determining the forms of the zones of the small apparatus, introduced by him into the Harbour Lights of France, and his own mode of rigorously solving some of the preliminary questions involved in the computations; but put me in possession of various important suggestions, which substantially embrace the whole subject. Another friend also helped me, by pointing out certain less direct methods of determining some of the elements, which greatly abridged the labours of computation. Mr Fresnel agreed with me in anticipating a considerable increase of the light derived from the accessory part of the apparatus; but he expressed his opinion, that in order to prevent great absorption, the rings should not greatly exceed those of the small apparatus in their sectional area. This would have required about forty rings to intercept the same quantity of light acted upon by the curved mirrors; and, although the difficulties of grinding were somewhat similar to those which had already been encountered in forming the cylindric belt for the Isle of May apparatus, there were also some special difficulties attending[268] the formation of the Catadioptric Zones. catadioptric zones, which appeared so formidable as to deter me by the expense of grinding so many zones, and led me to think of adopting flint glass. Considerable masses, of a very pure and homogeneous appearance, had been shewn to me by the late Dr Ritchie of the London University, who calculated upon the uniform and permanent success of his process; but, whatever foundation there might have been for this hope, it was removed by his death, which occurred soon afterwards, and I was forced to return to the idea of using crown glass. In order, therefore, to enable me to estimate more correctly the advantage of the zones, I procured from Messrs Cookson of Newcastle, an average specimen of crown glass, of the thickness of 40 mm. (about 1¹⁄₂ inch), which is the distance traversed by the ray between its immergence into and its emergence out of the zones of the small apparatus; and having had it carefully polished, with both faces parallel, I found, as the result of numerous trials, conducted with every precaution I could think of, that the loss of light due to the transmission through it, was somewhat less than ²⁄₇ths of the incident light. According to the experiments of Bougeur, the loss by the two refractions may be assumed at ¹⁄₂₀th; so that we could not sensibly err in concluding that the whole loss due to the transmission of the light through the zones would not much exceed ²⁄₇ths of the incident light. In the lights of the first order, the loss by reflection from the surface of the mirrors, and by the escape of light through the interstices which separate them, is not less than ²⁄₃ds of the light incident on that part of the apparatus. On the most moderate expectation, therefore, which this proportion seemed to warrant, it appeared that, without any allowance for imperfections in the figure of the zones, at least twice as much light would be transmitted through the zones as can be reflected by the mirrors. The prospect even of a part of this increase being obtained without the expenditure of more oil, seemed too important to be readily renounced, more especially when it was considered that the fixed lights, to which it chiefly applies, are[269] necessarily much feebler than the revolving lights, as well as more numerous and more expensive. So many motives pressed me to the work, that I commenced my labours (during my leisure hours while engaged at the Skerryvore), and computed Tables of the Elements of 45 zones, whose lesser sides were 40 millimètres in length, which were printed in 1840. In 1841, in consequence of having seen at Paris specimens of purer crown glass, I printed other Tables from computations of larger zones, which I had made in 1838, but had discarded as unsuited to the inferior quality of English glass, whose absorption rendered the use of smaller dimensions of the zone imperative. In the first Table, I had adopted the form of isosceles triangles, to avoid the difficulty of grinding annular surfaces with radii of great length (which I found required to be nearly 30 feet), but in the second Table, I adopted a suggestion, conveyed to me in a letter from M. Leonor Fresnel, by giving each zone the form of an oblique triangle whose base is the chord of the circle which osculates the surface of the reflecting side of the zone. Some attempts were made by Messrs Cookson at Newcastle to execute the largest of the zones; but the forms differed so widely from the dimensions assigned in the Table, that I had begun to despair of success. About this time, I received a communication from M. Fresnel, pointing out several inaccuracies in my Tables, and more especially directing my attention to the disadvantage of choosing, for the focus of the upper series of zones, a high part of the flame, as I had done with the view of throwing all the light below the horizon, so that none might be lost. He, at the same time, informed me of the success of M. François Soleil, in executing zones for the smaller apparatus, known by the name of the Third Order; and put me in possession of the results of his computations of large zones of the First Order, suited to the greatly improved quality of the crown glass of St Gobain, with an invitation, before I should adopt his dimensions, to verify his calculations. This I willingly undertook, and computed the elements of the zones in M. Fresnel’s Table afresh, with results differing from his only in one or[270] two instances, to an amount whose angular value does not exceed more than 2″. The Table in the Appendix contains the result of my calculations, which are verifications of those of M. Fresnel. The subject of the zones has thus been very fully weighed; and it is most satisfactory to think that complete success has attended the perseverance and ardour of M. François Soleil, who at once boldly undertook to furnish for the Skerryvore Lighthouse the first catadioptric apparatus ever constructed on so magnificent a scale. On the 23d December 1843, M. Fresnel announced, in a letter to me, the complete success which had attended a trial of the apparatus at the Royal Observatory at Paris, whereby it appeared that the illuminating effect of the cupola of zones, was to that of the seven upper tiers of mirrors of the first order, as 140 to 87. Nothing can be more beautiful than an entire apparatus for a fixed light of the first order, such as that shewn in Plates XVII. and XVIII. It consists of a central belt of refractors, forming a hollow cylinder 6 feet in diameter, and 30 inches high; below it are six triangular rings of glass, ranged in a cylindrical form, and above a crown of thirteen rings of glass, forming by their union a hollow cage, composed of polished glass, 10 feet high and 6 feet in diameter! I know no work of art more beautiful or creditable to the boldness, ardour, intelligence, and zeal of the artist.
I must now endeavour to trace the various steps by which the elements of the zones given in the appended Table have been determined; and this, I fear, I cannot do without considerable prolixity of detail. Referring to Plates XV., XVI., XVII., and XVIII., in which F shews the flame, RR, the refractors, and MRM and MRM, the spaces through which the light would escape uselessly above and below the lens, but for the corrective action of the mirrors MM, which project the rays falling on them to the horizon, I have to observe that a similar effect is obtained, but in a more perfect manner, by means of the zones ABC and A₂B₂C₂ (fig. 71, on page 271), whose action on the divergent rays of the lamp causes the rays FC, FB and FC₂, FB₂ to emerge horizontally, by refracting[271] them at the inner surfaces BC, B₂C₂, reflecting them at AB, A₂B₂, and a second time refracting them at AC, A₂C₂.
Fig. 71.
The problem proposed is, therefore, the determination of the elements and position of a triangle ABC, which, by its revolution about a vertical axis, passing through the focus of a system of annular lenses or refractors in F, would generate a ring or zone capable of transmitting in an horizontal direction by means of total reflection, the light incident upon its inner side BC from a lamp placed in the point F. The conditions of the question are based upon the well-known laws of total reflection, and require that all the rays coming from the focus F shall be so refracted at entering the surface BC, as to meet the side BA at such an angle, that instead of passing out they shall be totally reflected from it, and passing onwards to the side CA shall, after a second refraction at that surface, finally emerge from the zone in an horizontal direction. For the solution of this problem, we have given the positions of F the focus, of the apex C of the generating triangle of the zone, the length of the side BC or CA, and the refractive index of the glass. The form of the zone must then be such as to fulfil the following conditions:—
1. The extreme ray FB must suffer refraction and reflection at B, and pass to C, where being a second time refracted, it must follow the horizontal direction CH.
[272]
2. The other extreme ray FC must be refracted in C and passing to A, must at the point be reflected, and a second time reflected, so as to follow the horizontal course AG (see fig. 72, on opposite page).
These two propositions involve other two in the form of corollaries.
1. That every intermediate ray proceeding from F, and falling upon BC in any point E, between B and C, must, after refraction at the surface BC in E into the direction EW, be so reflected at W from AB into the direction WI, that being parallel to BC, it shall, after a second refraction in I, at the surface AC, emerge horizontally in the line IK.
And, 2. That the paths of the two extreme rays must therefore trace the position of the generating triangle of the zone.
To these considerations it may be added, that as the angles BCH and FCA are each of them solely due to the refraction at C, as their common cause, they must be equal to each other, and BCA being common to both, the remaining angle ACH = the remaining angle BCF.
We naturally begin by the consideration of the lowest ray FC, whose path being traced gives the direction of the two refracting sides BC and AC, leaving only the direction of the reflecting side BA to be determined. I shall not now explain the reason for neglecting entirely the consideration of the reflecting side at present, as I could not do so without anticipating what must be more fully discussed in the sequel; but I may content myself with stating, that as the positions of BC and AC depend upon the direction of the incident ray FC, and on the refractive index of the glass, this part of the investigation may be carried on apart from any interference with the reflecting side.
As we know the relation existing between the angles of incidence and refraction, we might determine the relative positions of the sides AC and BC, by means of successive corrections obtained by protraction, tracing the paths of the rays from the horizontal[273] directions backwards through the zones to the focus. This method, however, depends entirely upon accurate protraction, and is therefore unsatisfactory as a final determination, or if employed for any other purpose than that of affording a rough approximation to the value of the angle, a knowledge of which may occasionally save trouble in the employment of more exact means of determination. I have not, however, on any occasion employed this process, as I found that a little practice enabled me to make my first estimation very near the truth. I shall therefore at once proceed to give a view of the reasoning employed in the investigation.
Fig. 72.
Referring to fig. 72, which shews the first and second zone of the upper series, we have
Tan LCF = FLCL;
and if we make
| the known angle, | SCF = α |
| OCF = ξ = the complement of BCF = the angle of incidence for FC. | |
| DCΟ = γ = angle of refraction. | |
| LCF = θ = (HCF - 90°) = (2 α - 90°) | |
| SCD = (α + γ - ξ) | |
| And | m = the index of refraction for crown glass, |
we obtain the means of determining the angles γ and ξ in two equations, which are based upon the relation between the angles of incidence[274] and refraction, and on the interdependence of the various angles about C. These primary equations are:
sin ξ = m . sin γ
and
[66]γ = 2 ξ - θ (making 2 α - 90° = θ)
[66] The truth of the first of these equations (sin ξ = m . sin γ) which merely expresses the ratio of the sines of the angles of incidence and refraction is obvious; but owing to the great number of small angles about C, a little consideration may be required to enable one to perceive the truth of the second. I therefore subjoin the steps by which I reached it. It is obvious (see fig. 72), that as ACH and BCF are equal, the line SC bisecting HCF must bisect ACB. But the production of AC clearly gives SCD opposite and equal to ACW and SCD is by construction = (α - ξ + γ) = (α + γ - ξ), and, therefore, ACB, which is twice ACW or SCD = (2 α + 2 γ - 2 ξ). Now, by construction OC is a normal to the refracting surface CB and its production C g gives AC g = γ. But γ = ACB - g CB = (2 α + 2 γ - 2 ξ) - g CB = (2 α + 2 γ - 2 ξ) - 90°, hence
| γ | = | {2 α + 2 γ - 2 ξ} - 90°, |
| and γ - 2 γ | = | -γ = -2 ξ + (2 α - 90°) by transposition, and finally changing signs, we have as above: |
| γ | = | 2 ξ - (2 α - 90°) |
| = | 2 ξ - θ. |
Eliminating γ between these two equations we obtain:
sin ξ = m . sin (2 ξ - θ)
an expression, which, after various transformations of circular functions, assumes the form
sin⁴ ξ - 1m sin θ . sin³ ξ + (1 4 m² - 1) . sin² ξ + 12 m sin θ . sin ξ + ¹⁄₄ sin² θ = 0[67]
[67] This expression is equivalent to that of M. Fresnel, but owing to a simplification in the fractional coefficients, it is not literally the same. I was led to it by the following steps, starting from the original equation sin ξ = m sin (2 ξ - θ)
| sin ξ | = | m sin (2 ξ - θ) |
| = | m{sin 2 ξ . cos θ - cos 2 ξ sin θ} | |
| = | m cos θ . sin 2 ξ - m sin θ . cos 2 ξ | |
| = | m cos θ . 2 sin ξ . cos ξ - m sin θ . {1 - 2 sin² ξ} | |
| = | 2 m cos θ . sin ξ . cos ξ - m sin θ + 2 m sin θ . sin² ξ. |
Therefore, m sin θ + sin ξ - 2 m sin θ sin² ξ = 2 m cos θ . sin ξ . cos ξ.
Then:
m² sin² θ + 2 m sin θ . sin ξ - 4 m² sin² θ sin² ξ + sin² ξ - 4 m sin θ . sin³ ξ + 4 m² sin² θ . sin⁴ ξ = 4 m² cos² θ sin² ξ (1 - sin² ξ) = 4 m² . cos² θ . sin² ξ - 4 m² cos² θ sin⁴ ξ.
Hence we have:
m² sin² θ + 2 m sin θ . sin ξ + (1 - 4 m²) . sin² ξ - 4 m sin θ . sin³ ξ + 4 m² sin⁴ ξ = 0
Then dividing by 4 m² and arranging according to powers of ξ, we have as above:
sin⁴ ξ - 1 m sin θ . sin³ ξ + (1 4 m² - 1) . sin² ξ + 12 m . sin θ . sin ξ + ¹⁄₄ sin² θ = 0
[275]
The solution of this equation, which is of the fourth degree, is somewhat tedious; but as the root, which will satisfy the optical conditions of the question, must be the sine of an angle, and necessarily lies between zero and unity; and as the protraction, if conducted with due care in the manner already described, affords the means of at once assuming a probable value of ξ not very distant from the truth, the labour of the calculation, in this particular case, is not quite so great as might be expected. But notwithstanding all the abridgments of which the particular case admits, a considerable amount of labour is required, and a corresponding risk of error incurred, in merely introducing the numerical values into the equation preparatory to its solution; and any other method requiring less arithmetical operation, is, of course, greatly to be preferred. I therefore willingly adopted the suggestion of a friend, the benefit of whose advice I have on many occasions experienced, and made use of the following ordinary method of approximating to the root of the equation.
If the equation sin ξ - m sin (2 - θ) = 0 (see page 274) be regarded as an expression for the error, when the true value of ξ which would satisfy the equation has been introduced into its first member, we may consider any error in the value of ξ as expressed by the equation:
sin ξ - m . sin (2 ξ - θ) = ε
and differentiating this expression we have:
| d ε | = | cos ξ . d ξ - 2 m cos (2 ξ - θ) . d ξ |
| = | {cos ξ - 2 m cos (2 ξ - θ)} . d ξ |
[276]
Then dividing by the differential coefficient we obtain
d ξ = d ε cos ξ - 2 m cos (2 ξ - θ)
But when ξ becomes ξ + d ξ, ε will also become ε + d ε; but
ε + d ε = 0
therefore d ε = -ε
hence by substitution we have
d ξ = -ε cos ξ - 2 m cos (2 ξ - θ)
d ξ = -{sin ξ - m sin (2 ξ - θ)} cos ξ - 2 m cos (2 ξ - θ)
d ξ = -sin ξ + m sin (2 ξ - θ) cos ξ - 2 m cos (2ξ - θ)
By substituting, therefore, in this last equation the known values of m and θ, and the assumed value of ξ, a correction is obtained, which being applied to ξ and the same process repeated, new corrections may be found until the value of d ξ falls within the limits of error, which may be considered safe in the particular case. I need hardly say, that where so great a body of flame is employed as in the lights of the first order, these limits are soon passed, more especially as one soon acquires by a little experience the means of guessing a value of ξ not very far from the truth. It is this method I have employed in calculating the appended tables of the zones, in which I have on all occasions, though, perhaps, with needless exactness, pushed my angular determinations to seconds.
Having in this manner determined the angles of BCF, the obtuse angle BCA of the generating triangle of the zone is easily and directly deduced by the following expression, which results from the obvious relations existing among the known angles about C; and we have (see fig. 73),
BCA = 90° + γ = 90° + 2 ξ - θ.
We next proceed to consider the form of BA, the reflecting side of the zone, which is a point of the greatest consequence, as an error in the inclination of any part of its surface is doubled in the[277] resulting direction of the reflected rays. The conditions of the question require, that every ray EW, after reflection at the surface AB, shall, like WI, be parallel to the first ray, which is reflected in the direction BC, and after a second refraction at C, emerges horizontally in CH. But, let us trace backwards the rays as they emerge in their horizontal directions IK, and it is obvious that if BA be made a straight line, then will every ray EW meet the first refracting side BC at the same angle, and there suffering the same refraction, they will go on parallel to each other, and never meet in the focus F. This convergence to F, which is a necessary condition of the problem, may, however, be produced by a curvature of AB, such that all the rays shall have a degree of convergence before falling on BC, sufficient to cause them to be finally refracted, so as to meet in F. On this account, they will occupy less space in passing through BC, than they did in passing through AC; and thus BC will be shorter than AC by some quantity which shall give to that part of AB which is at B the amount of downward inclination required for causing the ray BF finally to converge to F; and the line joining B and A must be a curve, every point of which has its tangent inclined so as to serve the same purpose.
Fig. 73.
To trace tangents to this curve, is therefore the next step in the process. The direction of the first tangent AZ depends upon very simple considerations; and all that is necessary to be done is to draw a line AU (fig. 73), parallel to BC (which is the parallel to the direction of the reflected rays), and forming an angle CAU, which is, of course, equal to the inclination of the extreme rays refracted by CB at C, with rays[278] reflected from the arc which we have yet to trace. The line AX bisecting this angle, must therefore be a normal to the reflecting surface at A, and AB drawn perpendicular to AX, is consequently a tangent to the reflecting arc.
We must next find the direction of the second tangent Z b, which must be so inclined that the ray F b will, after refraction at b, be reflected into the direction, b C; but as the rigorous determination of this is difficult, I shall describe two approximations suggested to me by M. Leonor Fresnel. The first method is based upon assuming the inclination of the ray refracted at b to the ray refracted at C as equal to:
b FCm
(in which expression, m is the refractive index of the glass); a supposition which obviously differs very little from the truth, as small arcs may be assumed as nearly equal to their sines. Now, it will be recollected, that the rays refracted at C and b, must be reflected at A and b, in a direction parallel to C b, and therefore the inclination of the reflecting surfaces, or that which should be formed by the tangents ZA and Z b, being half that of the incident rays, is, according to the assumption, equal to b FC2 m, which may be expressed by ¹⁄₃ b FC, m being equal to 1·51. But as the inclination of the two radii AX and BX is equal to the inclination of the tangents of the reflecting surfaces to which they are normals, we obtain for the excess B β of the secant of the reflecting arc over its radius the following expression:
Bβ = ¹⁄₂ AB . tan ¹⁄₃ BFC.[68]
The value of B b gives, of course, the direction of the second tangent Z b (which must be equal in length to AZ), whence we easily deduce the chord of the reflecting side A b.
[68] The following steps will shew the mode of obtaining this expression: Suppose (fig. 74, on opposite page) F n to be a ray incident on the surface BC very near b or B (which, although exaggerated in the figure for more easy reference, are close together), and let this ray F n be refracted in the direction n O, and draw n n′ parallel to CA, the ray which is refracted at C, then will n′ n O = m . b FC = ²⁄₃ b FC. But the tangent AZ should make with the tangent b Z an angle equal ¹⁄₃ b FC, or one-half the inclination of the rays refracted at b and C, which are afterwards by the agency of those tangents, to be reflected in the directions parallel to b C and to each other. Hence we have AX b (which is the inclination of the normals to those tangents),
or AX b = BZ b = b FC 2 m = b FC 3 nearly.
Fig. 74.
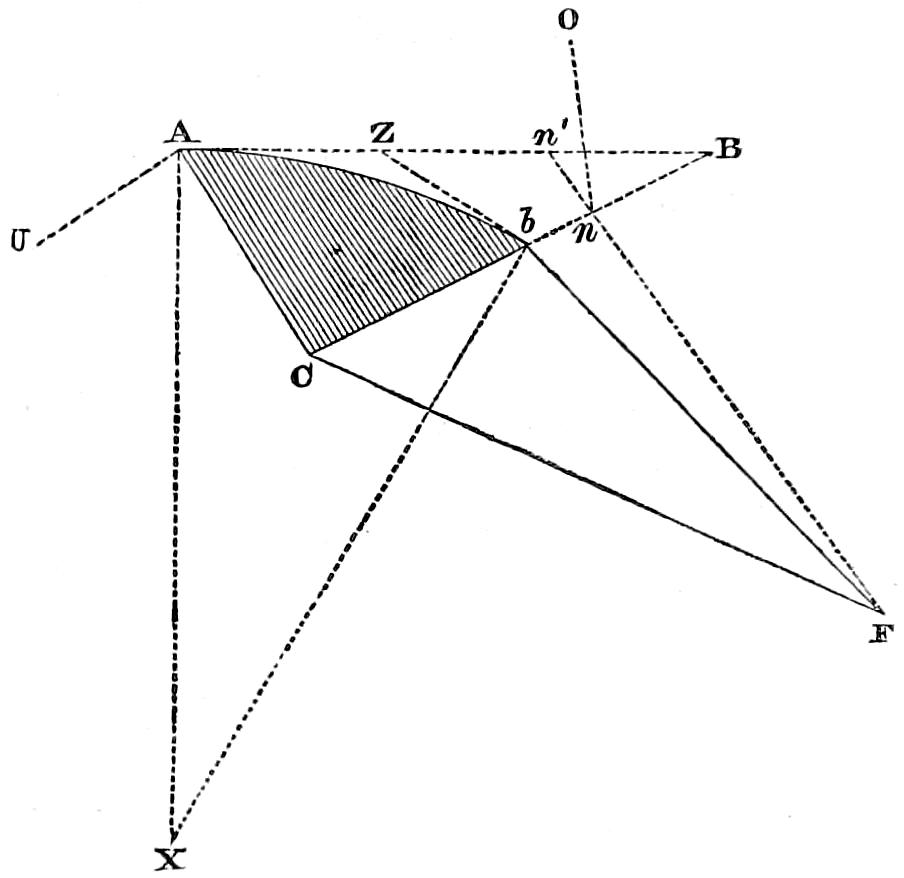
But putting AXB (fig. 73, p. 277) for AX b, and BFC for b FC, a supposition which may be safely made when the differences are so small, and founding upon the analogy
AX ∶ AB ∷ R ∶ tan AXB, we have BA = AX . tan AXB = AX . tan ¹⁄₃ BFC. Then
| AB² | = | B β (B β + 2 AX) |
| = | B β² + 2 B β . AX |
and neglecting B β², which is very small, we have:
BA² = B β . 2 AX nearly,
hence B β = BA²2 AX
But as above AX = BAtan ¹⁄₃ BFC
and substituting this value of AX we obtain:
B β = BA² 2 BAtan ¹⁄₃ BFC
hence we have, as in the text,
B β = ¹⁄₂ BA . tan ¹⁄₃ BFC
[279]
The second mode proposed by M. Fresnel, and that which I found most convenient in practice, consists in forming successive hypotheses as to the length of the side BC, and tracing the path of the incident ray FB, which being refracted at B, so as to make with the normal BK an angle = BKY = y′, and finally reflected in the direction BC, must make the angle YBZ = MBC. I shall describe[280] it as follows: In the annexed figure (fig. 75) MBZ is a tangent to the reflecting surface at B, and KBF is the angle of incidence of the ray BF before its refraction at B. If KBF = x´, and the angle of incidence of FC = ECF = x, we have BFC (which is the inclination of those rays to each other, and must be equal to the difference of their angles of incidence to the same surface) = x - x´, whence knowing x, we easily find a value of x´ corresponding to the length of BC. Then for finding the angle of refraction KBY = y´ we have:
sin y´ = sin x´m
Fig. 75.
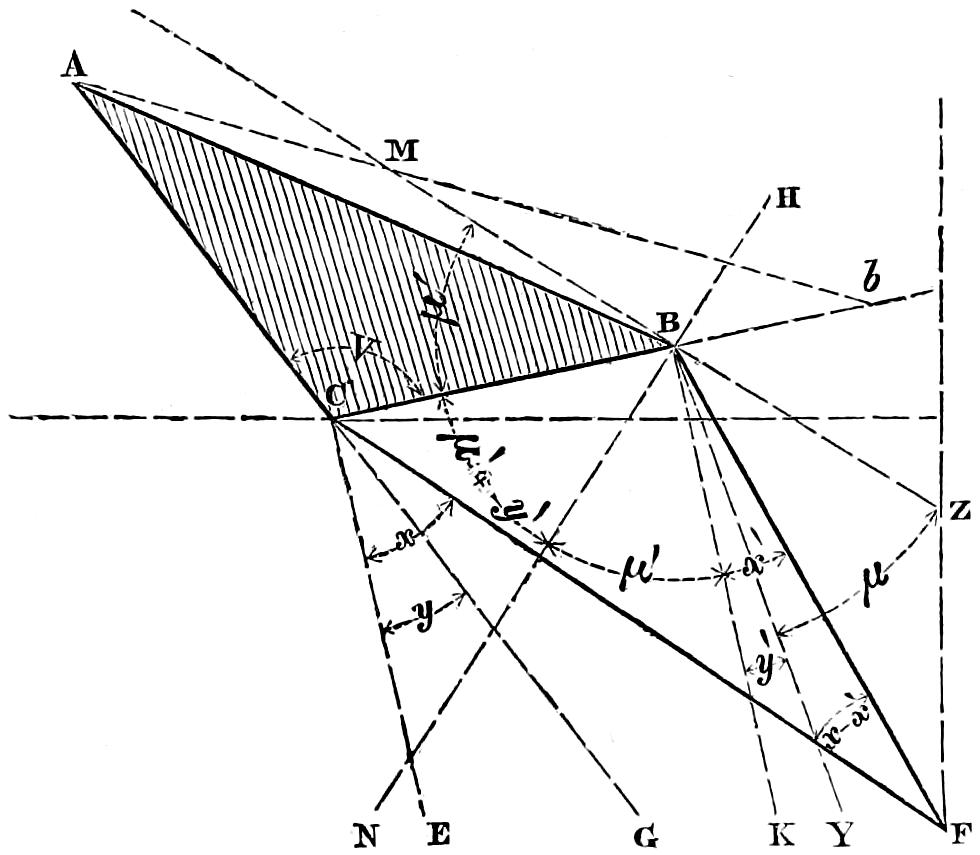
Now, if FB be refracted, so as to make with the reflecting side an angle equal to ZBY, it must (if the position of B be rightly chosen), be reflected so as to follow BC, thus making MBC = YBZ, and calling each of these angles = μ, we have the right angle NBZ made up of μ + y´ + NBK. But NBK clearly equals μ, because it is the inclination of the normals to BC and BZ, and hence y´ + 2 μ = 90°. This, therefore, forms a crucial test for the length of BC. I may only remark, that we already know the numerical value of y; and that of μ is easily found, for μ = CBA + ABM = CBA + BAM = CBA + (MAC - BAC) = CBA + ¹⁄₂ (180° - υ) - BAC. Thus knowing μ and y´, we have only to see whether
(y´ - 2 μ) - 90° = 0
We have now only to find the length of the radius AX or b X (see fig. 73, p. 277), which will describe the reflecting surface or arc AZ b, and to determine the position of its centre X. We already know the values of y′ and y, the angles of refraction of C[281] and b, and their difference y - y′ gives us the inclination of the rays which are to be reflected (into directions parallel to C b) at b and at A. This quantity is, of course, double the inclination of tangents to the reflecting surface AZ and b Z, and of their normals AX and b X. Again, we have the chord line
A b = AC . sin AC b sin (b CA);
and, as above,
AX b = ¹⁄₂ y - y′ = φ
And AX = b X = ρ = A b . sin ¹⁄₂ (180° - φ) sin φ = ¹⁄₂ A b . cosec ¹⁄₂ φ.
And, lastly, for the co-ordinates to X, the centre of curvature for the reflecting arc, we have
| OX | = | ρ . sin OAX |
| and OA | = | ρ . cos OAX.[69] |
[69] The angle OAX is easily found, as will be seen by referring to fig. 73, p. 277; for, AH being horizontal by construction and AO vertical, HAO = 90°; and HAC and CAU being both known, we have
OAX = 90° - (HAU + UAX) = 90° - (HAU + ¹⁄₂ CAU).
Fig. 76.
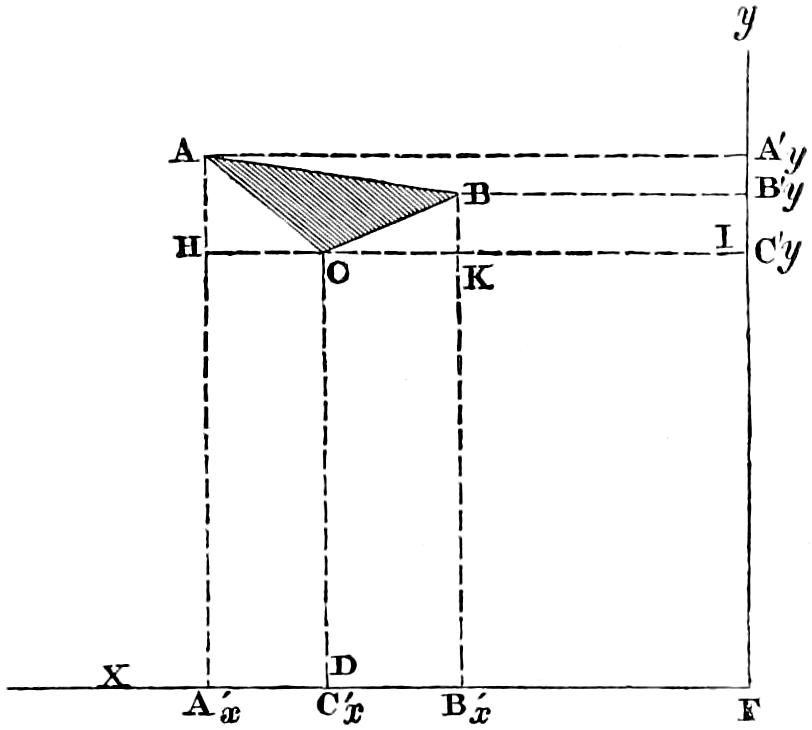
The positions of the apices A and B of the angles of the zones are also easily found in reference to the focus, and are given in the Table in the Appendix. In fig. 76 we may, in reference to the known position of C, find that of A or B, by simply adding the quantities AH, HC, and BK, to C y or C x, and by deducting CK from C y; while it is obvious that those quantities are respectively proportional to the length of the known sides AC and BC, modified by the inclination of those sides with the horizon. Hence we have AH = AC . sin ACH; HC = AC . cos ACH; BK = BC . sin BCK; and CK = BC . cos BCK.
In the process of grinding the zones, it is found convenient for[282] the workman to give a curved form to the refracting sides BC and AC, the one being made convex and the other concave, so that both being ground to the same radius, the convergence of the rays produced by the first shall be neutralized by the divergence caused by the second. By this arrangement we have three points given in space from which, with given radii, to describe a curvilinear triangle whose revolution round the vertical axis of the system generates the zone required. Co-ordinates to those two centres of curvature for the surfaces AC and BC were determined in reference to arris A of each zone, and will be found in the Appendix. The mode of finding those co-ordinates is, of course, similar to that already given; and, the radii being assumed at 4000 millimètres, the co-ordinates are respectively proportional to the sine and cosine of the inclination of the radius at A to the vertical line, which inclination depends upon the relations of known angles around A and C.
The section ABC (fig. 71, p. 271) of the first zone being thus determined, we proceed by fixing the point C₂ of the second zone, which is at the intersection of the horizon GAG₂ with the ray FBC₂ passing through B. This arrangement prevents any loss of light between the adjacent zones. The calculation of the elements of the second and of every following zone, is precisely similar to that of the first.
The mode of grinding the zones I shall not notice here; but shall refer the more curious reader to the Appendix, in which I have given the details of the process followed by M. Theodore Letourneau, who now manufactures the apparatus for the Northern Lights Board, in the room of M. François Soleil, who is engaged at St Petersburg in the same work. I accordingly proceed to consider what mode should be followed in Testing of Zones. testing the accuracy of the zones. For this purpose, various expedients suggested themselves, such as the application of gauges in the form of a radius, having at one end a plate with a triangular space cut through it, equal and similar to the cross section of the zone. The horizontal motion of this arm would, of course, detect the inaccuracies of the[283] successive sections of the inclosed zone. The application of such a gauge, however, seemed difficult, and in order to test the form of the zones, I satisfied myself with using callipers (similar to the sliding rules used by shoemakers) for measuring the length of the sides of the zone, and a goniometer for the angles, which is represented in the figure (fig. 77), in which ABC represents the prism, with one angle inclosed between the arms AC and AB, moveable round a centre O, and RR the graduated limb. This instrument is inconvenient and defective, as the convexity of the sides AB and BC of the zone requires some skill in getting the arms to be tangents to them.
Fig. 77.
Fig. 78.
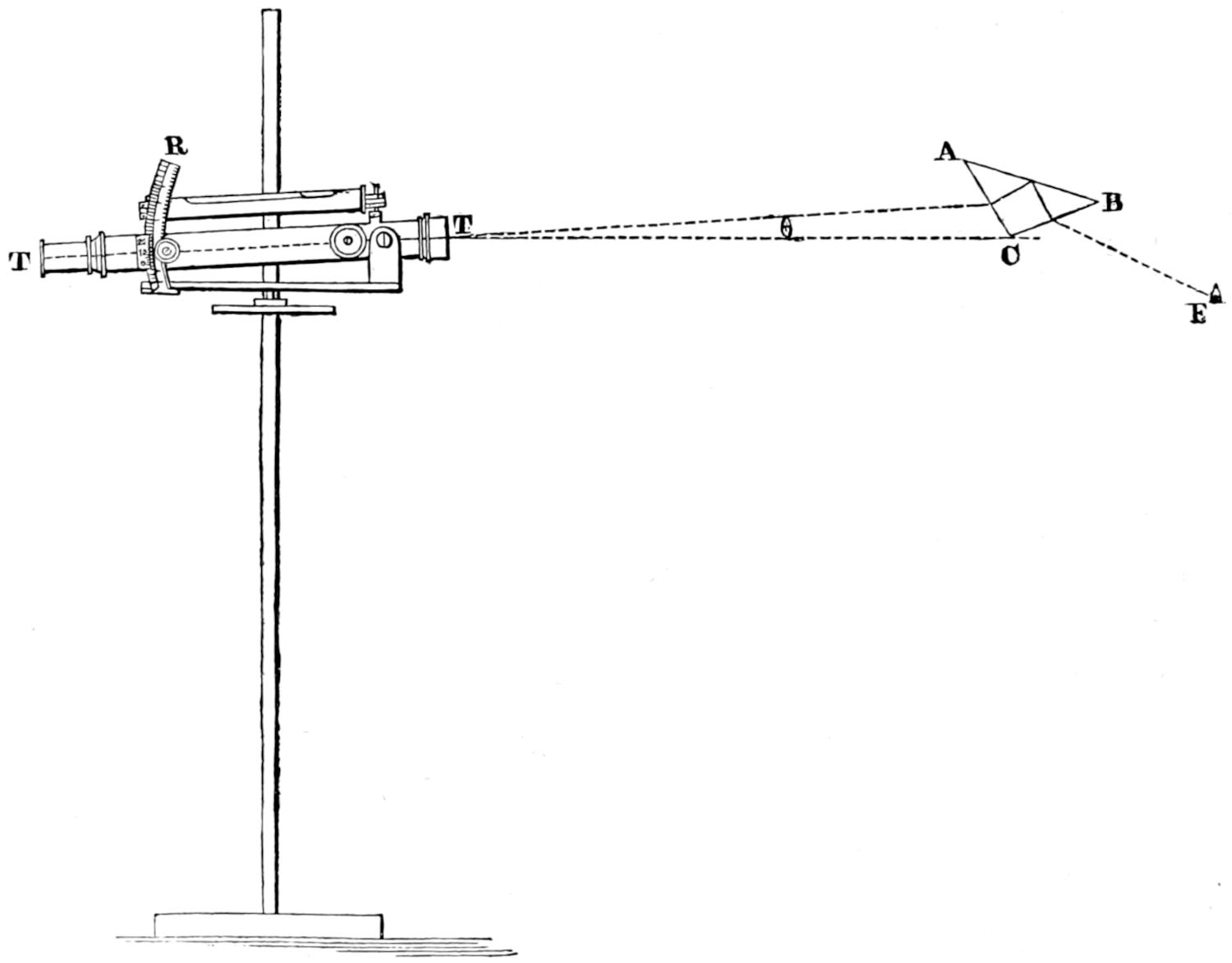
A practical test, however, yet remained to be made of the zones when fixed in the brass frames (shewn at Plate XVIII.), and assembled around the common focus of the system, by measuring the final inaccuracy in the path of the rays emergent from them. I have successfully used the following mode. Having mounted the frames containing the zones on a carriage revolving round a small flame placed truly in the common focus, I carefully marked with a piece of soap the centre of the emergent surface of each zone; and having attached to a vertical rod of metal a telescope, provided with a spirit-level and cross-hairs (for cutting the centre of the image of the flame reflected through the zone) in such a manner as to be capable of sliding on the rod, I observed the cutting of the centre of the flame by the cross-hairs. In the case of any aberration from a normal emergence of the central ray, I had thus the means of at once determining its amount and direction. The telescope was moved up or down, and its vertical inclination was varied until the axis of the instrument coincided with the direction of the ray emergent from the centre of each zone, which was made to circulate round the flame, the observer noting any change in the position of the reflected image of the flame, and causing an[284] attendant to mark the zones in which the change occurred, that they might again be subjected to separate examination of the same kind, by adjusting the telescope to the error of each. The vertical inclination of the telescope and the consequent aberration of the ray, was then measured by a graduated arc, with an adjusting spirit-level, moved by a rack and pinion. The accompanying figure (fig. 78) shews the arrangement just described. E is the small flame in the focus; ABC is the zone; TT is the telescope; and R a graduated limb, on which is read the angular deviation θ of the axis of the telescope from the horizon. In the figure, the ray emergent from the centre of AC is shewn dipping below the true level, to which the line TC is supposed to be parallel. I have succeeded by this method in detecting the inaccurate position of some of the zones in the frame; and the error has been reduced by carefully resetting them, so as to diminish considerably the error of a great proportion of the emergent rays. Another mode, and that which, owing to its convenience, was chiefly employed in preference to that just described, was to measure the vertical inclination (given in the Table in the Appendix), of each surface of the zone,[285] and more especially the reflecting surface, by means of the instrument, shewn in figures 79 and 80, after the zones were fixed in their place. The figure (No. 79) shews the mode of gauging the reflecting side AB of a zone of the upper series; and the second (No. 80) shews the position of the instrument in gauging the reflecting side AB of a zone of the under series. In those figures, L is a spirit-level; R, a graduated limb for reading the angular deviation from the true inclination of the tangents to each surface; and SS are studs which rest on the convex surfaces AB and BC of the zones, so as to make the ruler parallel to the tangents of those sides. I have only to add, that I have restricted the error, in the position of the reflecting side of the zones, to 50′ as an extreme limit; and I have invariably endeavoured, in altering the position of the zone in the frame, to throw any error on the side of safety, by causing the rays to dip below the horizon, rather than to rise above it.[70]
Fig. 79.
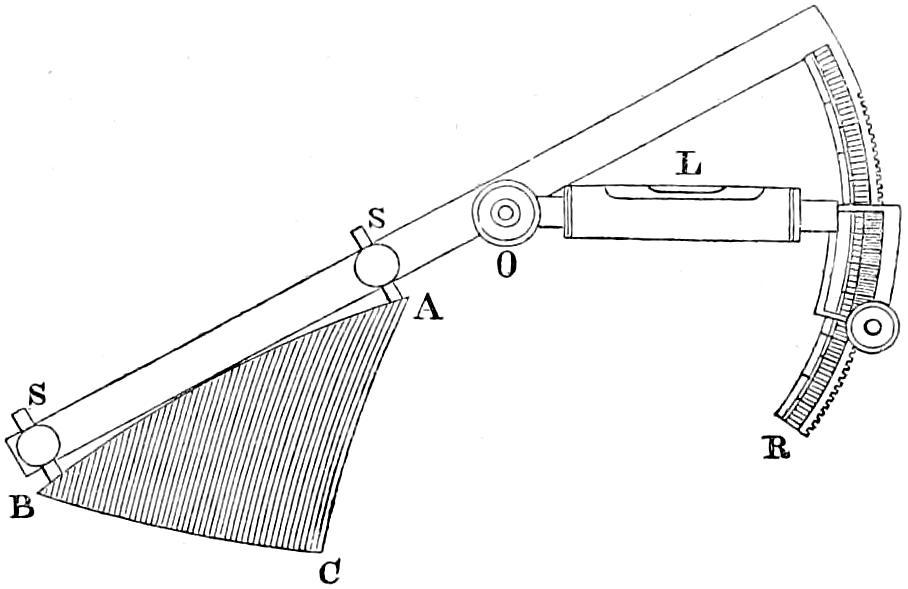
Fig. 80.
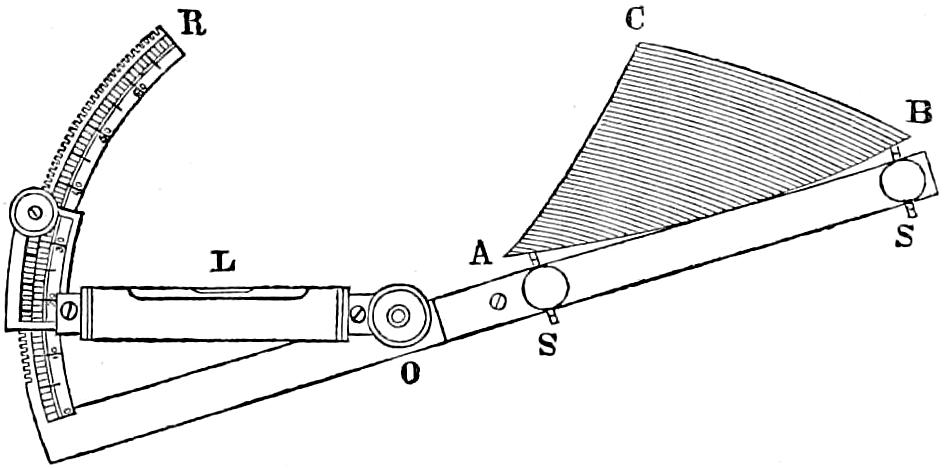
[70] In connection with the use of the clinometer, I determined the inclinations of the tangents or chords of the three curve surfaces AB, BC, and AC of each zone with NP, the axis of the system, by means of the obvious relations of the known angles about C, A, and B. Those inclinations (fig. 81) are shewn by the angles BNO, BON, and CPF; and are given in the Table of the Zones in the Appendix.
Fig. 81.
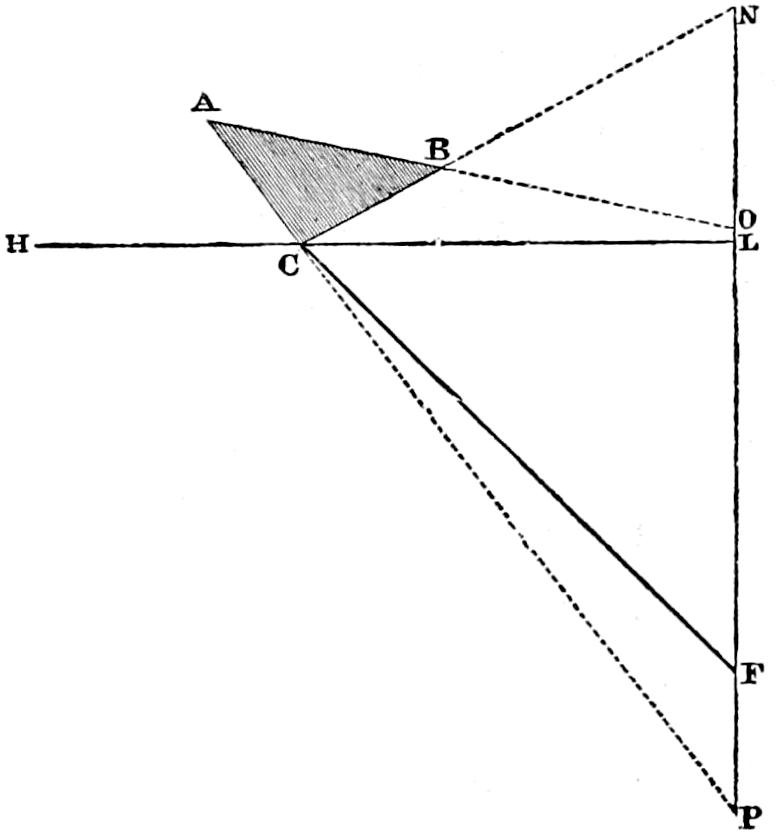
[286]
Framing of Zones. The mode of framing the greater zones is shewn in Plate XVIII. and is nearly the same as that used for the Small Harbour Light apparatus of the fourth order (Plate XIX.). The chief difference consists in the diagonal framing, which I adopted for supporting the cupola of 13 zones, which, from its great weight, could not be safely made to rest on the dioptric belt below. That frame is seen in Plates XVII. and XVIII. and is in accordance with the mode of jointing the refractors already described. This system has now been rendered still more complete by the adoption of lanterns composed of diagonal framework, afterwards described and shewn at Plate XXVI.
Mechanical Lamp. We have next to consider the great Lamp, to the proper distribution of whose light, the whole of the apparatus, above described, is applied. Fresnel immediately perceived the necessity of combining with the dioptric instruments which he had invented, a burner capable of producing a large volume of flame; and the rapidity with which he matured his notions on this subject and at once produced an instrument admirably adapted for the end he had in view, affords one of the many proofs of that happy union of practical with theoretical talent, for which he was so distinguished. Fresnel himself has modestly attributed much of the merit of the invention of this Lamp to M. Arago; but that gentleman, with great candour, gives the whole credit to his deceased friend, in a notice regarding lighthouses, which appeared in the Annuaire du Bureau des Longitudes of 1831. The lamp has four concentric burners, which are defended from the action of the excessive heat, produced by their united flames, by means of a superabundant supply of oil, which is thrown up from a cistern below by a clockwork movement and constantly overflows the wicks, as in the mechanical lamp of Carcel. A very tall chimney is found to be necessary, in order to supply fresh currents of air to each wick with sufficient rapidity to support the combustion. The carbonisation of the wicks, however, is by no means so rapid as might be expected, and it is even found that after they have suffered a good deal, the flame is not sensibly diminished, as the great heat[287] evolved from the mass of flame, promotes the rising of the oil in the cotton. I have seen the large lamp at the Tour de Corduan burn for seven hours without being snuffed or even having the wicks raised; and, in the Scotch Lighthouses, it has often, with Colza oil, maintained, untouched, a full flame for no less a period than seventeen hours.
Fig. 82.
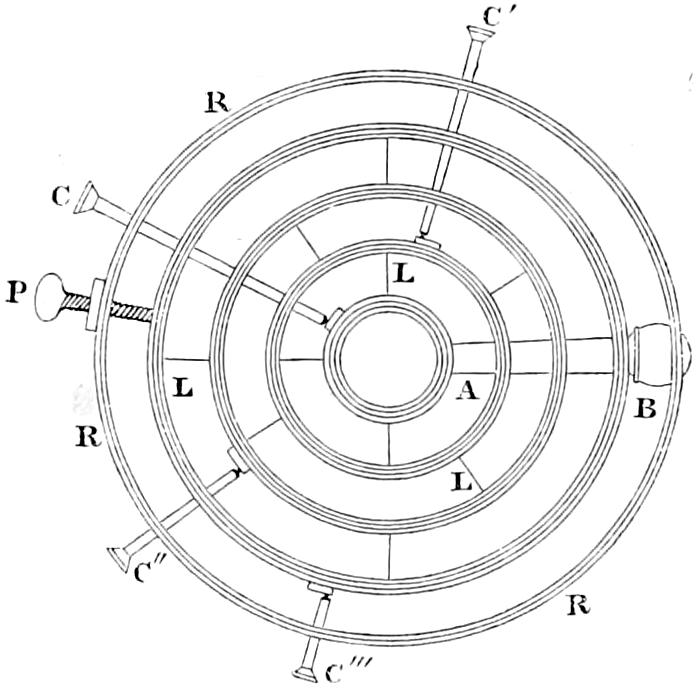
Fig. 83.
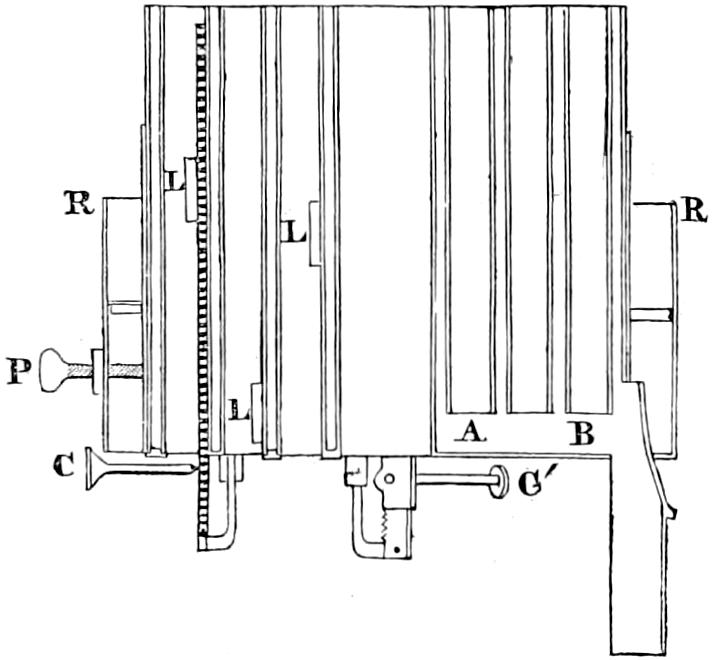
Fig. 84.
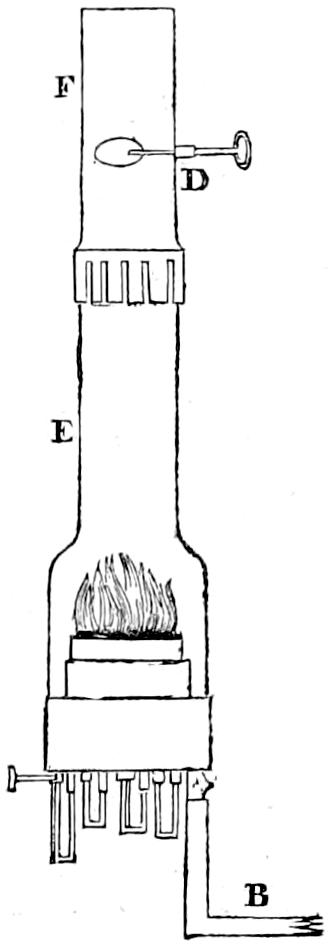
The annexed diagrams will give a perfect idea of the nature of the concentric burner. The first (fig. 82) shews a plan of a burner of four concentric wicks. The intervals which separate the wicks from each other and allow the currents of air to pass, diminish a little in width as they recede from the centre. The next (fig. 83) shews a section of this burner. C, C′, C″, C‴ are the rack-handles for raising or depressing each wick; AB is the horizontal duct which leads the oil to the four wicks; L, L, L, are small plates of tin by which the burners are soldered to each other, and which are so placed as not to hinder the free passage of the air; P is a clamping screw, which keeps at its proper level the gallery R, R, which carries the chimney. The last figure (No. 84) shews the burner with its glass chimney and damper. E is the glass chimney; F is a sheet-iron cylinder, which serves to give it a greater length, and has a small damper D, capable of being turned by a handle, for regulating the currents of air; and B[288] is the pipe which supplies the oil to the wicks. The only risk in using this lamp arises from the liability to occasional derangement of its leathern valves that force the oil by means of clockwork; and several of the lights on the French coast, and more especially the Corduan, have been extinguished by the failure of the lamp for a few minutes, an accident which has never happened, and scarcely can occur with the fountain lamps which illuminate the reflectors. To prevent the occurrence of such accidents, and to render their consequences less serious, various precautions have been resorted to. Amongst others, an alarum is attached to the lamp, consisting of a small cup pierced in the bottom, which receives part of the overflowing oil from the wicks, and is capable, when full, of balancing a weight placed at the opposite end of a lever. The moment the machinery stops, the cup ceases to receive the supply of oil, and, the remainder running out at the bottom, the equilibrium of the lever is destroyed, so that it falls and disengages a spring which rings a bell sufficiently loud to waken the keeper should he chance to be asleep. It may justly be questioned whether this alarum would not prove a temptation to the keepers to relax in their watchfulness and fall asleep; and I have, in all the lamps of the dioptric lights on the Scotch coast, adopted the converse mode of causing the bell to cease when the clockwork stops. There is another precaution of more importance, which consists of having always at hand in the light-room a spare lamp, trimmed and adjusted to the height for the focus, which may be substituted for the other in case of accident. It ought to be noticed, however, that it takes about twenty minutes from the time of applying the light to the wicks to bring the flame to its full strength, which, in order to produce its best effect, should stand at the height of nearly four inches (10cm.). The inconveniences attending this lamp have led to several attempts to improve it; and, amongst others, M. Delaveleye has proposed to substitute a pump having a metallic piston, in place of the leathern valves, which require constant care, and must be frequently renewed. A lamp was constructed in this[289] manner by M. Lepaute, and tried at Corduan; but was afterwards discontinued until some further improvements could be made upon it. It has lately been much improved by M. Wagner, an ingenious artist whom M. Fresnel employed to carry some of his improvements into effect. In the dioptric lights on the Scotch coast, a common lamp, with a large wick, is kept constantly ready for lighting; and, in the event of the sudden extinction of the mechanical lamp by the failure of the valves, it is only necessary to unscrew and remove its burner, and put the reserve-lamp in its place. The height of this lamp is so arranged, that its flame is in the focus of the lenses, when the lamp is placed on the ring which supports the burner of the mechanical lamp; and as its flame, though not very brilliant, has a considerable volume, it will answer the purpose of maintaining the light in a tolerably efficient state for a short time, until the light-keepers have time to repair the valves of the mechanical lamp. Only three occasions for the use of this reserve-lamp have yet occurred.
Height of the flame of the Mechanical Lamp.The most advantageous heights for the flames in dioptric lights are as follows:—
| Inches. | ||||
|---|---|---|---|---|
| 1st Order, | 10 to 11 | centimètres | = | 3·94 to 4·33 |
| 2d Order, | 8 to 9 | ...... | = | 3·15 to 3·54 |
| 3d Order, | 7 to 8 | ...... | = | 2·76 to 3·15 |
Those heights of flame can be obtained only by a careful adjustment of the heights of the wicks and the relative levels of the shoulder of the glass-chimney and the burner, together with a due proportion for the area of the opening of the iron-damper which surmounts it. The wicks must be gradually raised during the first hours of burning to the level of 7 millimètres (0·27 inch) above the burner, a height which they may only very rarely and but slightly exceed. By raising the shoulder of the glass-chimney the volume of the flame is increased; but, after a certain height is exceeded, the flame, on the other hand, becomes reddish, and its[290] brilliancy is diminished. The height of the flame is decreased, and it becomes whiter by lowering the chimney. The chimney is lowered or raised by simply turning to the right or to the left the cylindric glass-holder in which it rests (see Plate XXV.). In regulating the flame, however, recourse is most frequently had to the use of the damper, by enlarging the opening of which the flame falls and becomes whiter and purer; while by diminishing its aperture, the contrary effect is produced. The area of the opening depends on the inclination of a circular disc capable of turning, vertically through a quadrant, on a slender axle of wire, which is commanded by the light-keeper by means of a fine cord which hangs from it to the table below. When the disc (see fig. 84, p. 287) is in a horizontal plane the chimney is shut, when in a vertical plane it is open; and each intermediate inclination increases or decreases the aperture.
I need scarcely add, that in order to produce the proper effect of a system of lenses or refractors, the vertical axis of the flame should Position of flame in reference to focus of apparatus. coincide with their common axis; and it is further necessary, in order to bring the best portion of the flame into a suitable position with reference to the apparatus, that the top of the burner should be quite level, and should stand below the plane of the focus in the following proportions, viz.:—
| For | 1st order, | 28 | millimètres | = | 1·10 | inches. |
| ... | 2d order, | 26 | ... | = | 1·02 | ... |
| ... | 3d order, | 24 | ... | = | 0·95 | ... |
Fig. 85.
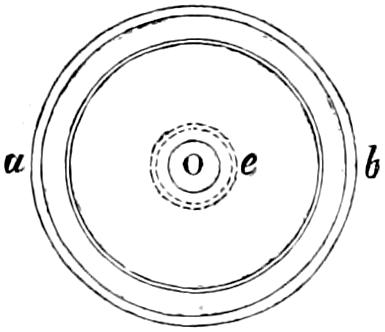
For the purpose of placing the lamp in the centre of the apparatus, a plumbet with a sharp point suspended in the axis of the apparatus, is used to indicate, by its apex, the place for the centre of the burner. The lamp is then raised or lowered as required by means of four adjusting screws Q at the bottom of its pedestal (Plate XX.); and the top of the burner is made horizontal by a spirit-level, the most convenient form of which is that of the spherical segment, which acts in every azimuth. Its application to[291] this purpose is due, I believe, to M. Letourneau, the successor of M. François in the construction of dioptric apparatus at Paris. This level is shewn in the annexed figure (fig. 85), in which a b is the brass frame containing the level, and O the air-bubble; and e shews circles of equal altitudes engraved on the glass. After the first application of this level, the adjustment of the burner as to its central position is carefully repeated by means of a centre gauge (shewn at fig. 90, p. 295), with reference to the vertex of each lens, or to many points on the internal surface of the refractors; and being found correct, the level is again applied to the top of the burner, to detect any deviation from horizontality that may have occurred during the process of adjusting it to the axis.
The lamp is subject to derangement, chiefly from the stiffness of the clack-valves for want of regular cleaning, bursting of the leathern valves of the oil-box, stiffness of the regulator, and the wearing of the bevelled gearing which gives motion to the connecting-rod that works the valves of the oil-pumps.
Working of the Pumps of the Lamp. The pumps of the lamp should raise, in a given time, four times the quantity of oil actually consumed by burning during that time. Their hourly produce should be,
| lb. avoirdupois. |
||
|---|---|---|
| For the lamp with | four wicks, | 6·615 |
| ...... | three wicks, | 4·410 |
| ...... | two wicks, | 1·675 |
This surplus of three times what is burned is necessary to prevent the wick from being carbonised too quickly; and it has been found quite sufficient for that purpose. The discharge from the pumps is, of course, regulated by changes in the angle of the fans of the regulator, or in the amount of the moving weight.
Care must be taken, in preparing the leathern valves of the pump-box or chamber, shewn in Plate XXII., that they be neither too flaccid from largeness nor too tense from smallness; and also that, after being fitted, they draw no air. To remove the old valves[292] and replace them by fresh ones, is a very simple process, more especially when a proper die or mould is used, which at once cuts the kid-leather, of which the valves are formed, to the required size and squeezes them into the proper shape. In Plates XX., XXI., XXII., XXIII., XXIV., and XXV., the most minute details are given as to the clockwork, pumps, burners, and flame of the great lamp.[71]
[71] See also M. Leonor Fresnel’s Instructions sur l’organisation et la surveillance du service des Phares et Fanaux de France. Paris, 1842, pp. 12, 13, 14, and 15.
The focal point for the lenses and refractors is in the centre of the flame and on the level of its brightest film, as shewn in Plate XXV. Choice of Focal Point for various parts of the apparatus. The choice of a focus for the zones naturally formed a most important practical consideration in their arrangement; and the judicious remarks of M. Leonor Fresnel on that subject, already noticed, would alone have induced me to discard my former calculations in favour of his. For the upper zones, M. Fresnel had adopted a point in the centre of the flame 10 millimètres above the focus of the lenses, so that all the light below that point necessarily falls between the horizon and the Lighthouse; but for the lower zones, it was necessary, owing to their arrangement for convenience in a cylindric form, to adopt a separate focus for each zone in the direction of the centre of gravity of that part of the flame which would light each zone. In this manner (fig. 86) the foci of the zones recede upwards from a to f in proportion to the depression of the zones a, b, c, d, e, f, so that the line joining each zone and its focus, must revolve as a radius vector round some point O between them. The details of this arrangement are shewn in Plate XVIII.; and are also given in the Table of the Catadioptric Zones in the Appendix.
Fig. 86.
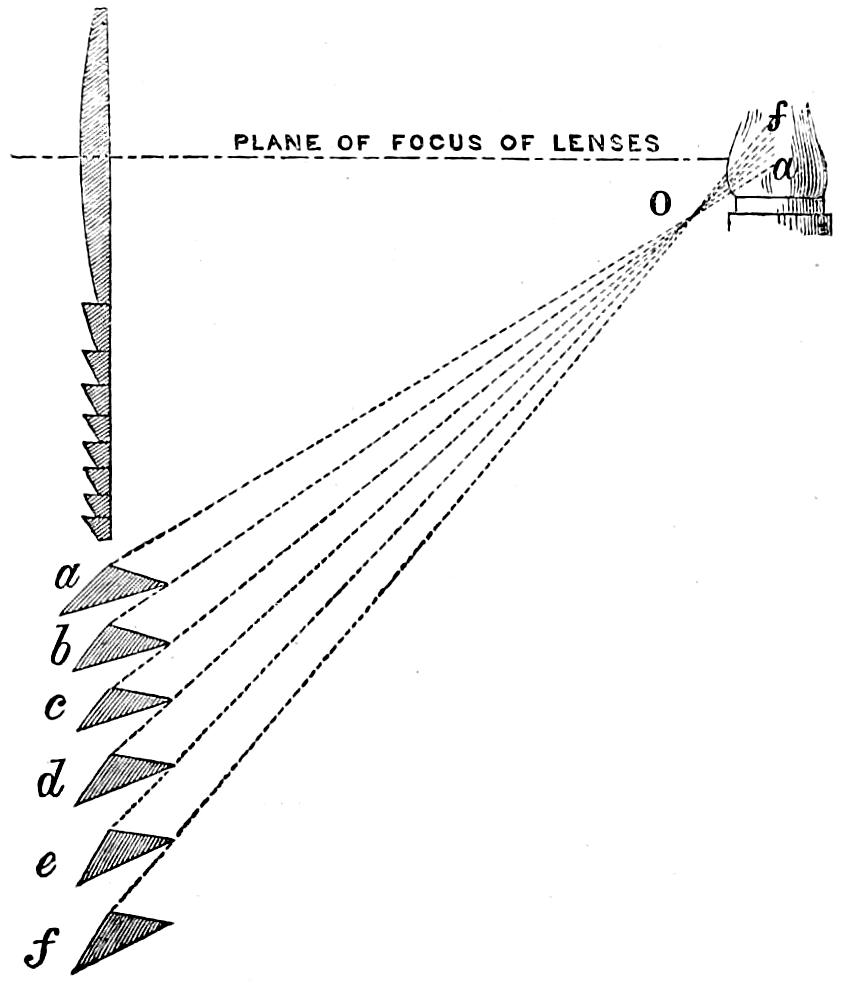
[293]
Fig. 87.
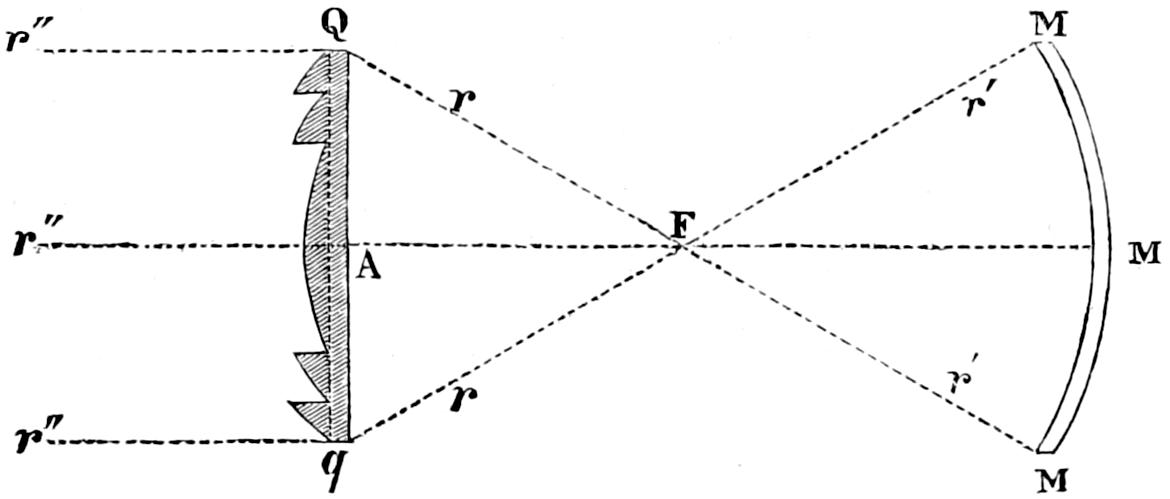
In the arc next the land, in fixed lights, a great loss of light ensues from the escape of the rays uselessly in that direction. So far back as 1834, I suggested the Application of Spherical Mirrors to fixed Dioptric Lights. placing a segment of a spherical mirror, with its centre of curvature coincident with F the focus of the system, so that the luminous pyramid MFM, of which the mirror MM forms the base, might be thrown back through the focal point and finally refracted into such a direction as to contribute to the effect of the lens QAq in seaward and opposite arc. In the diagram (fig. 87), r r indicate rays proceeding directly from F; r′ r′ rays reflected from MM through F, and finally refracted at QA q; and r″ r″ is the beam compounded of both. In the best glass-silvered mirrors, this accession of light would amount to nearly half of the light incident on them. In such an arrangement, a considerable radius is desirable to decrease the amount of aberration produced by a large flame. In the case of revolving lights of the first order, the radius would, of course, be limited to somewhat less than three feet, which is the focal distance of the lenses, between which and the focus, the reflecting segment must be placed; but in fixed lights, the lantern is the limit of radius, so that a focal length of five feet ten inches may be obtained. M. François ground some beautiful mirrors of three feet radius, which were afterwards tinned by his successor, M. Letourneau, by a new process discovered by himself;[72] and that gentleman is at present engaged in the construction of reflecting spherical segments 1200mm. square (about 16 superficial feet), to a radius of 1770mm. (5 feet 10 inches), which subtend a vertical arc of about 40°.
[72] See notice of a similar process practised about the year 1750 by Mr Rogers of London, ante, p. 240.
Arrangement of Dioptric Apparatus. The arrangements of the dioptric apparatus in the lightroom will be more fully understood by referring to the Plates.
Plate XIII. shews an elevation of a revolving dioptric apparatus of the first order; F is the focal point, in which the flame is placed;[294] L, L great annular lenses, forming by their union an octagonal prism, with the lamp in its axis, and projecting, in horizontal beams, the light which they receive from the focus; L′L′, the upper lenses, forming by their union a frustum of an octagonal pyramid of 50° of inclination, and having their foci coinciding in the point F. They parallelise the rays of light which pass over the lenses. M, M are plane mirrors, placed above the pyramidal lenses L′L′, and so inclined as to project the beams reflected from them in planes parallel to the horizon; Z, Z are the lower zones, first used at Skerryvore, in the room of the curved mirrors which were used at Corduan. The lower part of Plate XIII. shews the moveable framework which carries the lenses and mirrors, and the rollers on which it circulates, with the clockwork which gives motion to the whole. Plate XIV. is the plan of the apparatus shewn in Plate XIII.
Plate XV. shews a section of a fixed dioptric light of the first order. F is the focal point in which the flame is placed; R, R cylindric refractors, forming by their union a prism of thirty-two sides, or a true cylinder, with the lamp in its axis, and producing a zone of light of equal intensity in every point of the horizon; M, M, curved mirrors, ranged in tiers above and below the cylindric refractors, and having their foci coinciding in the point F; the effect of the mirrors increases the power of the light, by collecting and transmitting the rays which would otherwise pass above and below them, without increasing the effect of the light. Plate XVI. gives the elements of the curved mirrors MM of Plate XV.
After the details given of the nature of the catadioptric zones, all that is needful is briefly to refer to Plate XVII., in which ABC and A′B′C′ shew the upper and lower zones which supply the place of the mirrors shewn at M, M, in Plate XV.; while DEF shews the cylindric belt as lately improved, with the diagonal joints M, N, C; and X, X, represent the diagonal supports for the cupola ABC. This plate, in connection with the enlarged view of the same apparatus at Plate XVIII., affords a complete explanation of the arrangement of all the parts.
Arrangement of the Dioptric Apparatus in the Lightroom. For the purpose of arranging the various parts of the dioptric apparatus in their proper positions, three gauges are employed.[295] The first (fig. 88) is for ascertaining that the lenses l, l, meet at the proper horizontal angle, so that their axes shall meet with the proper inclination in F the focus. This is done by means of two arms, whose projecting points r, r, r, r touch the backs of the lenses, while the graduated arc c indicates the inclination of l, l, to l, l, or the complement of that inclination at F.
Fig. 88.
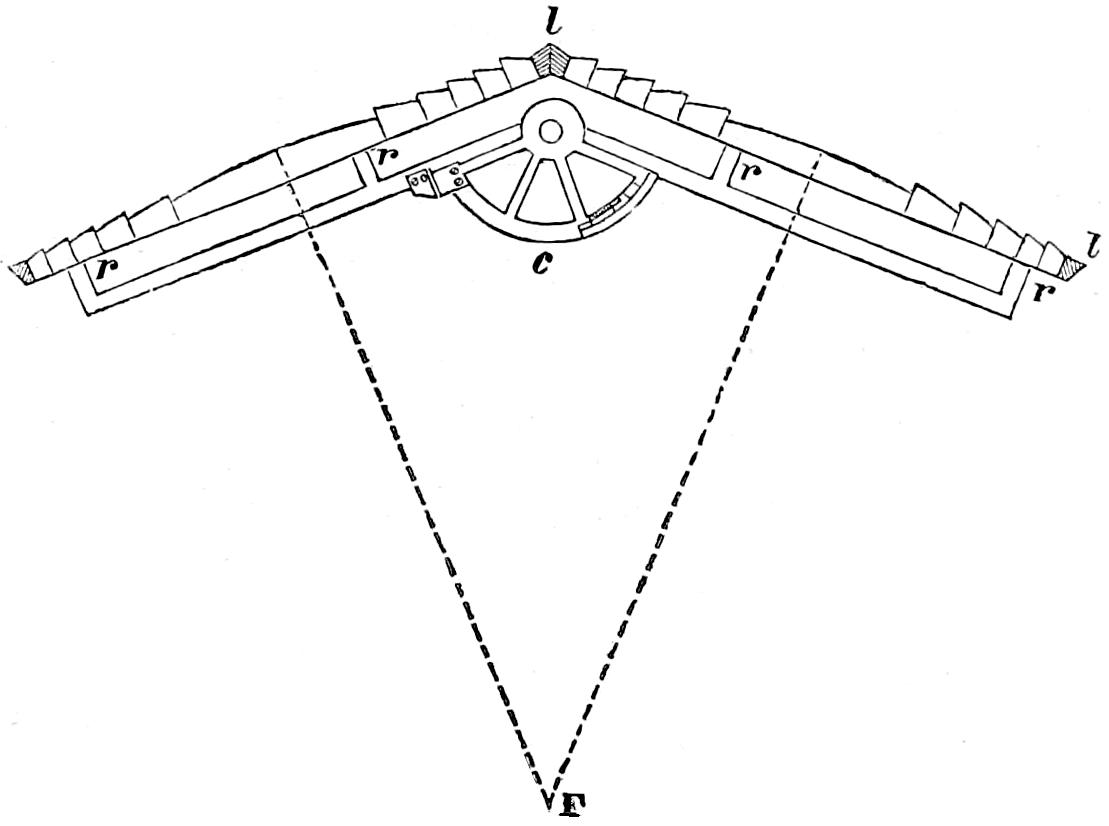
Fig. 89.
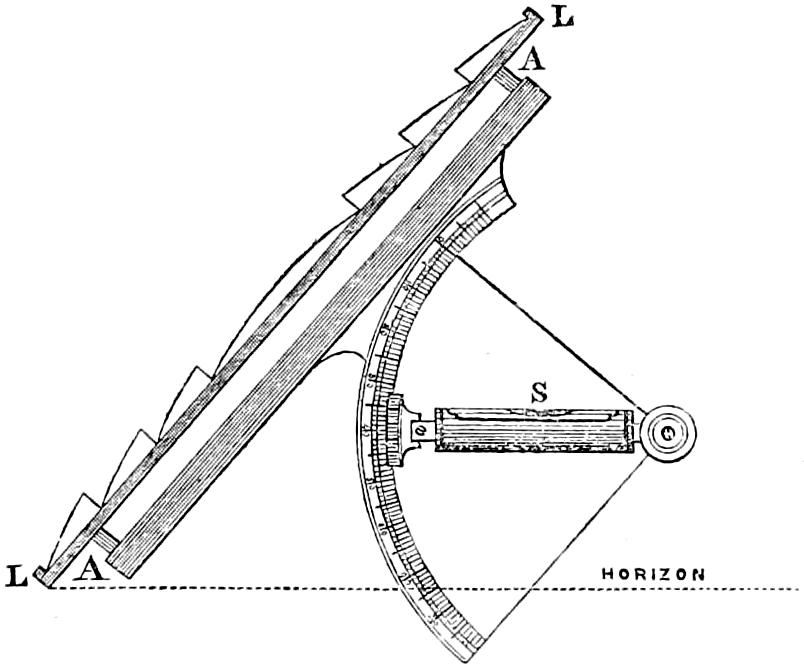
Again, for ascertaining the verticality of the main lenses, or for setting the subsidiary lenses or mirrors shewn in Plates XIII. and XIV., at the required angle of inclination, recourse is had to a clinometer (fig. 89) touching the back of the lens LL by means of studs at A, A, while the spirit-level S indicates, on the graduated limb, the amount of deviation from the vertical position of the instrument, whether accidental or intentional.
Fig. 90.
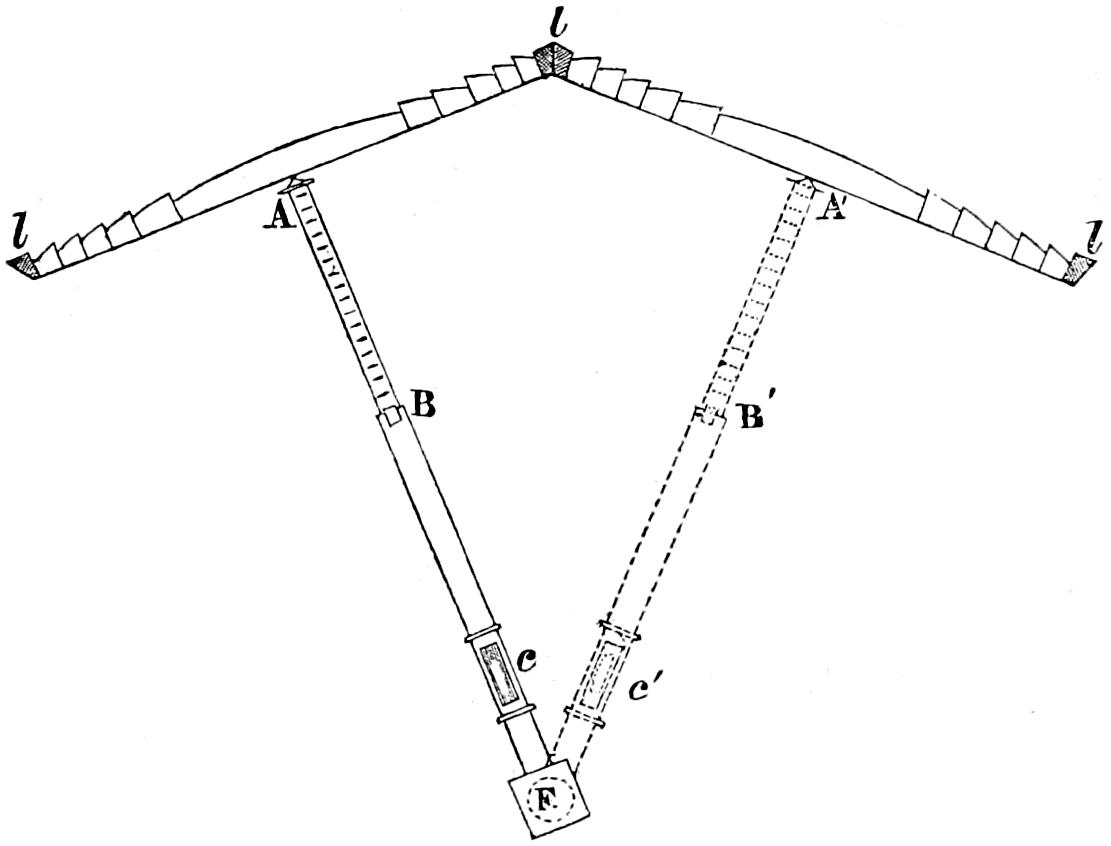
Lastly, to test the true position of the lamp itself, with reference to the lenses thus properly arranged, we apply a radius or trainer (fig. 90) which fits into the centre burner at F, while its point A touches the centre of the[296] lens l, l; at B is a graduated slide, which admits of the trainer being lengthened or shortened to suit various focal distances; and the spirit-level at c at once corrects any error in the length of the trainer arising from depression or elevation, and also serves to indicate the proper level for the burner which is noticed at page 290, in speaking of the lamp. The dotted line F c′ B′A′ shews the position of the trainer in reference to an adjacent lens.
The elegant apparatus invented by Augustin Fresnel for Harbour Lights, on the same principle as that just described for Sea Lights, is shewn beneath (fig. 91). It consists of thirteen rings of glass of various diameters arranged one above another, in an oval form. The five middle rings have an interior diameter of 11·81 inches (30cm.), and like those of the larger apparatus, refract equally over the horizontal plane of the focus the light which they receive from it. The other rings or prisms, five of which are upper and three lower, are ground and set in such a manner, that they project all the light derived from the focus in a direction parallel to the other rays by total reflection.
Fig. 91.
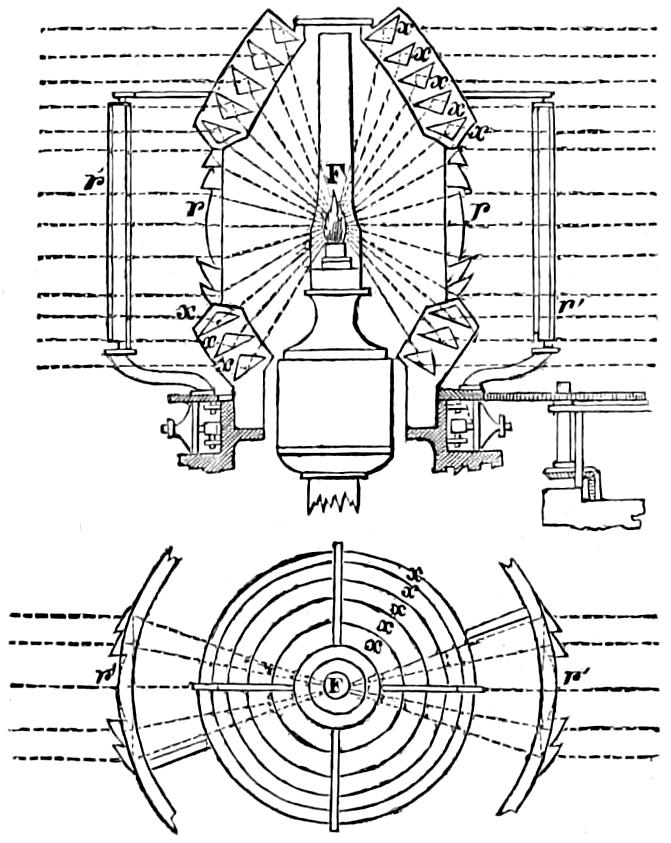
The arrangements of this apparatus, which is distinguished by the addition of external refractors arranged vertically, will be more fully understood by a reference to fig. 91, which shews its section and plan. F is the focal point in which the flame is placed; r, r cylindric refractors, forming by their union a cylinder with a lamp in its axis, and producing a zone of light of equal intensity all round the horizon; x, x are catadioptric prismatic rings acting by total reflection, and giving out zones of light of equal intensity at every point of the horizon. The dotted lines shew the course traversed by the rays of light which proceed from the lamp, and are acted upon by the rings of glass. The letters r′ r′ shew the external prisms,[297] having their axes at right angles to those of the principal bent prisms, composing the refractors at r, r, and revolving around them. This ingenious application of the property of crossed prism is already described at page 264.
When this apparatus is employed to light only a part of the horizon, the rings are discontinued on the side next the land, and room is thus obtained for using a common fountain lamp; but when the whole horizon is illuminated, the apparatus must inclose the flame on every side; and it has in that case been found most convenient to employ the hydrostatic lamp of Thilorier, which has a balance of sulphate of zinc in solution.
An instrument differing from this small apparatus only in size, has lately been introduced into the Lighthouses in France, and has also been adopted in Scotland for lights in narrow seas. It has the same number of rings of glass as the small apparatus, and of the same proportional dimensions. Its internal diameter, however, is 500 millimètres (about 19¹⁄₂ inches). Drawings of the smaller apparatus are given at Plate XIX., which also contains the radii and the centre of curvature for the rings of the central dioptric belt; while the following Table gives the elements of the eight prismatic zones (above and below the belt), with the co-ordinates to their centres of curvature, measured from the arris A of the outer or emergent surfaces, in whatever position the zone may lie on the lathe. The dimensions are in millimètres; but may be easily converted into imperial inches, in the manner described in the Table of the Great Zones, which will be found in the Appendix:—
[298]
| Number of Zone. |
Radii of curvature. |
Horizontal distance from the axis of the system. |
Vertical distance from the outer arris. |
Number of Zone. |
Radii of curvature. |
Horizontal distance from the axis of the system. |
Vertical distance from the outer arris. |
|---|---|---|---|---|---|---|---|
| Reflecting Surfaces (Convex). | |||||||
| I. | 1094·5 | 723·5 | 833·78 | V. | 1222·9 | 523·6 | 1169·1 |
| II. | 1045·7 | 652·8 | 891·01 | VI. | 1249·4 | 544·0 | 1192·1 |
| III. | 1044·5 | 598·4 | 933·67 | VII. | 1150·4 | 593·5 | 1062·9 |
| IV. | 1087·3 | 551·9 | 1010·20 | VIII. | 1113·6 | 650·5 | 985·9 |
| Outer Refracting Surfaces (Concave). | |||||||
| I. | 1250·0 | 1290·7 | 303·19 | V. | 1250·00 | 1100·22 | 829·52 |
| II. | 1250·0 | 1274·2 | 445·89 | VI. | 1250·00 | 1112·74 | 821·16 |
| III. | 1250·0 | 1234·0 | 587·05 | VII. | 1250·00 | 1190·50 | 698·00 |
| IV. | 1250·0 | 1173·0 | 717·71 | VIII. | 1250·00 | 1251·90 | 557·22 |
| Inner Refracting Surfaces (Convex). | |||||||
| I. | 1250·0 | 150·67 | 1211·90 | V. | 1250·00 | 452·23 | 1184·20 |
| II. | 1250·0 | 228·19 | 1208·80 | VI. | 1250·00 | 453·07 | 1185·20 |
| III. | 1250·0 | 305·10 | 1203·35 | VII. | 1250·00 | 374·60 | 1196·00 |
| IV. | 1250·0 | 381·00 | 1195·30 | VIII. | 1250·00 | 294·35 | 1203·80 |
Power of Dioptric Instruments. The effect of an annular lens, in combination with the great lamp, may be estimated at moderate distances to be nearly equal to that of 3000 Argand flames of about an inch diameter; that of a cylindric refractor at about 250; and that of a curved mirror may perhaps on an average be assumed at about 10 Argand flames.
Orders of the French Lights. The dioptric lights used in France are divided into four orders, in relation to their power and range; but in regard to their characteristic appearances, this division does not apply, as, in each of[299] the orders, lights of identically the same character may be found, differing only in the distance at which they can be seen, and in the expense of their maintenance. The four orders may be briefly described as follows:—
1st, Lights of the first order having an interior radius or focal distance of 36·22 inches (92cm.), and lighted by a lamp of four concentric wicks, consuming 570 gallons of oil per annum.
2d, Lights of the second order having an interior radius of 27·55 inches (70cm.), lighted by a lamp of three concentric wicks, consuming 384 gallons of oil per annum.
3d, Lights of the third order, lighted by a lamp of two concentric wicks, consuming 183 gallons of oil per annum. The instruments used in those lights are of two kinds, one having a focal distance of 19·68 inches (50cm.), and the other of 9·84 inches (25cm.).
4th, Lights of the fourth order, or harbour-lights, having an internal radius of 5·9 inches (15cm.), and lighted by a lamp of one wick, or Argand burner, consuming 48 gallons of oil per annum. This apparatus is, as already noticed, now more generally used of a larger scale, having a focal distance of 9·84 inches (25cm.), and a lamp of two concentric wicks, consuming about 130 gallons of oil per annum.[73]
[73] An apparatus of 0m.·185cm. was recently added to the list of French lights under the name of the Fifth order; while that of 25cm. radius has been called the Fourth, and that of 15cm. radius is styled the Sixth order. Those minute subdivisions I consider to be unnecessary.
Distinctions of the Dioptric Lights. Those four orders are not intended as distinctions; but are characteristic of the power and range of lights, which render them suitable for different localities on the coast, according to the distance at which they can be seen. This division, therefore, is analogous to that which separates our lights into sea-lights, secondary lights, and harbour-lights, terms which are used to designate the power and position, and not the appearance of the lights to which they are applied.
[300]
Each of the above orders is susceptible of certain combinations, which produce various appearances, and constitute the distinctions used for dioptric lights; but the following are those which have been actually employed as the most useful in practice:—
The first order contains, 1st, Lights producing, once in every minute, a great flash, preceded by a smaller one, by the revolution of eight great lenses and eight smaller ones combined with eight mirrors; 2d, Lights flashing once in every half minute, and composed of sixteen half lenses. Those lights may have the subsidiary parts simply catoptric, or diacatoptric; and, 3d, Fixed lights, composed of a combination of cylindric pieces, with curved mirrors or catadioptric zones ranged in tiers above and below them.
The second order comprises revolving lights with sixteen or twelve lenses, which make flashes every half minute; and fixed lights varied by flashes once in every four minutes, an effect which, as already noticed, is produced by the revolution of exterior cylindrical pieces.
The third order (larger diameter) contains common fixed lights, and fixed lights varied by flashes once in every four minutes.
The third order (smaller diameter) contains fixed lights, varied by flashes once in three minutes.
The fourth order has fixed lights varied by flashes once in every three minutes, and fixed lights of the common kind. It has been thought necessary to change the term “fixed lights varied by flashes,” for “fixed light with short eclipses,” because it has been found that, at certain distances, a momentary eclipse precedes the flash.
These distinctions depend upon the periods of revolution, rather than upon the characteristic appearance of the light; and therefore seems less calculated to strike the eye of a seaman, than those employed on the coasts of Great Britain and Ireland. In conformity with this system, and in consideration of the great loss of light which results from the application of coloured media, all distinctions based upon colour have been discarded in the French lights.
[301]
The distinctions are, in fact, only four in number, viz.: Fixed; Fixed, varied by flashes;[74] Revolving, with flashes once a minute; and Revolving, with flashes every half minute. To those might be added, Revolving, with bright periods once in two minutes, and perhaps Flashing once in five seconds (as introduced by me at the Little Ross, but I cannot say with such complete success as would induce me to recommend its general adoption). My own experience would also lead me to reject the distinction called “Fixed, varied by flashes,” which I do not consider as possessing a marked or efficient character.
[74] The “Feu fixe, varié par des éclats,” or “Feu fixe, à courtes éclipses,” of Fresnel.
Comparison of Dioptric and Catoptric Apparatus for Revolving Lights. Having thus fully described the nature of the catoptric and dioptric modes of illuminating lighthouses, I shall next compare the merits of both systems, with a view to determine their eligibility in revolving or in fixed lights.
Repeated experiments were made at Gullan-hill, which is distant from Edinburgh about fifteen miles, during the winters of 1832 and 1833, under the inspection of the Commissioners of Northern Lights, the result of which was, that the light of one of the great annular lenses used in the revolving lights of the first order, was equal to the united effect of about eight of the large reflectors employed in the revolving lights on the Scotch coast. It may be said, however, that the dia-catoptric[75] combination of pyramidal lenses and plane mirrors of Corduan, adds the power of more than two reflectors to the effect of the great lens; but it ought to be remembered that in the French lights, this additional power is used only to compensate for one of the defects of the system by lengthening the duration of the flash, and therefore contributes, if at all, only in a very indirect manner, to render the light visible to the mariner at a greater distance. M. Fresnel found, from the smaller divergence of the lens, that the eclipses were too long and the bright periods of the revolution too short; and he therefore determined to[302] adopt the horizontal deviation of 7° for the upper lenses, with a view to remedy this defect. Assuming, therefore, that it were required to increase the number of reflectors in a revolving light of three sides, so as to render it equal in power to a dioptric revolving light of the first order, it would be necessary to place eight reflectors on each face, so that the greatest number of reflectors required for this purpose may be taken at twenty-four. M. Fresnel has stated the expenditure of oil in the lamp of four concentric wicks at 750 grammes of colza oil per hour; and it is found by experience at the Isle of May and Inchkeith, that the quantity of spermaceti oil consumed by the great lamp, is equal to that burned by from fourteen to sixteen of the Argand lamps used in the Scotch lights. It therefore follows that, by dioptric means, the consumption of oil necessary for between fourteen and sixteen reflectors, will produce a light as powerful as that which would require the oil of twenty-four reflectors in the catoptric system of Scotland; and, consequently, that there is an excess of oil equal to that consumed by ten reflectors, or 400 gallons in the year, against the Scotch system. But in order fully to compare the economy of producing two revolving lights of equal power by those two methods, it will be necessary to take into the calculation the interest of the first outlay in establishing them.
[75] I use this word to designate the arrangement of pyramidal lenses and plane mirrors, by which the light is first refracted, and then reflected.
The expense of fitting up a revolving light with twenty-four reflectors, ranged on three faces, may be estimated at L.1298, and the annual maintenance, including the interest of the first cost of the apparatus, may be calculated at L.418, 8s. 4d. The fitting up a revolving light with eight lenses and the dia-catoptric accessory apparatus, may be estimated at L.1459, and the annual maintenance at L.354, 10s. 4d. It therefore follows, that to establish and afterwards maintain a catoptric light of the kind called revolving white, with a frame of three faces, each equal in power to a face of the dioptric light of Corduan, an annual outlay of L.63, 18s. more would be required for the reflecting light than for the lens light; while for a light of the kind called revolving red and white, whose[303] frame has four faces, at least thirty-six reflectors would be required in order to make the light even approach an equality to that of Corduan; and the catoptric light would in that case cost L.225 more than the dioptric light.
The effect produced by burning an equal quantity of oil, in revolving lights on either system, may be estimated as follows:—In a revolving light, like that of Skerryvore, having eight sides, each lighting with its greatest power a horizontal sector of 4°, we have 32° (or units) of the horizon illuminated with the full power of 3200 Argand flames, and consequently an aggregate effect of 102,400 flames, produced by burning the oil required for sixteen reflectors; while in a catoptric apparatus, like that of the old light at Inchkeith, having seven sides of one reflector, each lighting with its greatest power a sector of 4°·25′, we have nearly 31° (or units) of the horizon illuminated with the full power of 400 Argand flames, and consequently an aggregate effect of 12,400 flames as the result of burning the oil required for seven reflectors. Hence, the effect of burning the same quantity of oil in revolving lights on either system, will be represented respectively by 16 7 12,400 = 28,343 for the catoptric, contrasted with 102,400 for the dioptric light; or, in other words, revolving lights on the dioptric principle use the oil more economically than those on the catoptric plan, nearly in the ratio of 3·6 to 1.
Comparison of Catoptric and Dioptric Apparatus for Fixed Lights. I shall now speak of fixed lights, to which the dioptric method is peculiarly well adapted. The effect produced by the consumption of a gallon of oil in a fixed light, with twenty-six reflectors, which is the smallest number that can be properly employed, may be estimated as follows:—The mean effect of the light spread over the horizontal sector, subtended by one reflector, as deduced from measurements made at each horizontal degree, by the method of shadows, is equal to 174 unassisted Argand burners. If, then, this quantity be multiplied by 360 degrees, we shall obtain an aggregate effect of 62,640, which, divided by 1040 (the number of[304] gallons burned during a year in twenty-six reflectors), would give 60 Argand flames for the effect of the light maintained throughout the year by the combustion of a gallon of oil. On the other hand, the power of a catadioptric light of the first order, like that lately established at Girdleness, may be estimated thus:—The mean effect of the light produced by the joint effect of both the dioptric and catadioptric parts of a fixed light apparatus, may be valued at 450 Argand flames, which, multiplied by 360 degrees, gives an aggregate of 162,000; and if this quantity be divided by 570 (the number of gallons burned by the great lamp in a year), we shall have about 284 Argand flames for the effect of the light produced by the combustion of a gallon of oil. It would thus appear that in fixed lights, the French apparatus, as lately improved, produces, as the average effect of the combustion of the same quantity of oil over the whole horizon, upwards of four times the amount of light that is obtained by the catoptric mode; although, in certain directions, opposite the axis of each reflector, the catoptric light be fully 50 per centum more powerful than the dioptric light.
But the great superiority of the dioptric method chiefly rests upon its perfect fulfilment of an important condition required in a fixed light, by distributing the rays equally in every point of the horizon. In the event of the whole horizon not requiring to be illuminated, the dioptric light would lose a part of its superiority in economy, and when half the horizon only is lighted, it would be more expensive than the reflected light; but the greater power and more equal distribution of the light, may be considered of so great importance, as far to outweigh the difference of expense. In the latter case, too, an additional power (as noticed p. 293) can be given to the dioptric light, by placing at the landward side of the lightroom, spherical mirrors with their centres in the focus of the refracting apparatus.[76] The luminous cones, or pyramids of which[305] such reflectors would form the bases, instead of passing off uselessly to the land, would thus be thrown back through the focal point, and finally refracted, so as to increase the effect of the light seaward, by nearly one-third of the light which would otherwise be lost.
[76] A similar arrangement can also be made in revolving lights by making the radius of the mirrors somewhat less than that of the inscribed circle of the octagon bounded by the lenses, so that they may circulate freely round the backs of the mirrors. The shortness of the radius of the reflecting surface would, of course, increase the divergence of the beam of light refracted through the lenses, as the flame would, in this case, subtend a greater angle at the face of the mirrors.
The expense of establishing a fixed light composed of twenty-six reflectors, may be estimated at L.950, and its annual maintenance, including interest on the first cost of the apparatus, may be reckoned at L.425, 10s.: and the expense of fitting up a fixed light on the dioptric principle with catadioptric zones is L.1511, while its annual maintenance may be taken at L.285, 6s. 4d. It thus appears that the annual expenditure of the dioptric fixed light is L.140, 3s. 8d. less than that of a fixed light composed of twenty-six reflectors; while the average effect, equally diffused over the horizon, is four times greater.
The comparative views already given of the catoptric and dioptric modes of illuminating lighthouses, demonstrate that the latter produces more powerful lights by the combustion of the same quantity of oil; while it is obvious that the catoptric system insures a more certain exhibition of the light, from the fountain-lamps being less liable to derangement than the mechanical lamps used in dioptric lights. The balance, therefore, of real advantages or disadvantages, and, consequently, the propriety of adopting the one or the other system, involves a mixed question, not susceptible of a very precise solution, and leaving room for different decisions, according to the value which may be set upon obtaining a cheaper and better light, on the one hand, as contrasted, on the other, with less certainty in its exhibition.
Summary of considerations as to the fitness of the two systems for Revolving Lights. A few general considerations, serving briefly to recapitulate the arguments for and against the two systems, may not be out of[306] place. And, first, regarding the fitness of dioptric instruments for revolving lights, it appears from the details above given,—
1st, That by placing eight reflectors on each face of a revolving frame, a light may be obtained as brilliant as that derived from the great annular lens; and that, in the case of a frame of three sides, the excess of expense by the reflecting mode, would be L.63, 18s.; and in the case of a frame of four sides, the excess would amount to L.225.
2d, That for burning oil economically in revolving lighthouses, which illuminate every point of the horizon successively, the lens is more advantageous than the reflector in the ratio of 3·6 to 1.
3d, That the divergence of the rays from the lens being less than from the reflector, it becomes difficult to produce, by lenses, the appearance which characterises the catoptric revolving lights, already so well known to British mariners; and any change of existing lights which would, of course, affect their appearance, must, therefore, involve many grave practical objections which would not at all apply to the case of new lights.
4th, That the uncertainty in the management of the lamp renders it more difficult to maintain the revolving dioptric lights without risk of extinction, an accident which has several times occurred at Corduan and other lighthouses both in France and elsewhere.
5th, That the extinction of one lamp in a revolving catoptric light is not only less probable, but leads to much less serious consequences than the extinction of the single lamp in a dioptric light; because, in the first case, the evil is limited to diminishing the power of one face by an eighth part; whilst, in the second, the whole horizon is totally deprived of light. The extinction of a lamp, therefore, in a dioptric light, leads to evils which may be considered infinitely great in comparison with the consequences which attend the same accident in a catoptric light.
Summary of considerations as to the fitness of the two systems for Fixed Lights. In comparing the fixed dioptric, and the fixed catoptric apparatus, the results may be summed up under the following heads:—
[307]
1st, It is impossible, by means of any practicable combination of paraboloïdal reflectors, to distribute round the horizon a zone of light of exactly equal intensity; while this may be easily effected, by dioptric means, in the manner already described. In other words, the qualities required in fixed lights cannot be so fully obtained by reflectors as by refractors.
2d, The average light produced in every azimuth by burning one gallon of oil in Argand lamps, with reflectors, is only about one-fourth of that produced by burning the same quantity in the dioptric apparatus; and the annual expenditure is L.140, 3s. 8d. less for the entire dioptric light than for the catoptric light.
3d, The characteristic appearance of the fixed reflecting light in any one azimuth would not be changed by the adoption of the dioptric method, although its increased mean power would render it visible at a greater distance in almost every direction; the only exception being in the azimuths opposite the axis of each reflector, where the catoptric light has an excess of power equal to about 50 per centum.
4th, From the equal distribution of the rays, the dioptric light would be observed at equal distances in every point of the horizon; an effect which cannot be fully attained by any practicable combination of paraboloïdal reflectors.
5th, The inconveniences arising from the uncertainty which attends the use of the mechanical lamp, are not perhaps so much felt in a fixed as in a revolving light, because the greater simplicity of the apparatus admits of easier access to it, in case of accident.
6th, But the extinction of a lamp in a catoptric light, leaves only one twenty-sixth part of the horizon without the benefit of the light, and the chance of accident arising to vessels from it, may, therefore, be considered as incalculably less than the danger resulting from the extinction of the single lamp of the dioptric light, which deprives the whole horizon of light.
7th, There may also, in certain situations, be some risk arising from irregularity in the distances at which the same fixed catoptric[308] light can be seen in the different azimuths. This defect, of course, does not exist in the dioptric light.
Advantages and disadvantages of both systems under certain circumstances. There can be little doubt, that the more fully the system of Fresnel is understood, the more certainly will it be preferred to the catoptric system of illuminating lighthouses, at least in those countries where this important branch of administration is conducted with the care and solicitude which it deserves. It must not, however, be imagined, that there are no circumstances in which the catoptric system is not absolutely preferable to illumination by means of lenses. We have hitherto attended only to horizontal divergence and its effects, and this is unquestionably the more important view; but the consideration of vertical divergence must not be altogether overlooked. Now, while it is obvious that vertical divergence, at least above the horizon, involves a total loss of the light which escapes uselessly upwards into space, it is no less true, that if the sheet of light which reaches the most distant horizon of the lighthouse, however brilliant, were as thin as the absence of all vertical divergence would imply, it would be practically useless; and some measure of dispersion in the arc below the horizon is therefore absolutely indispensable to constitute a really useful light. In the reflector, the greatest vertical divergence below the horizontal plane of the focus is 16° 8′, and that of the lens is about 4° 30′.
Let us consider for a moment the bearing of those facts upon the application of the two modes of illumination to special circumstances. The powerful beam of light transmitted by the lens, peculiarly fits that instrument for the great sea-lights which are intended to warn the mariner of his approach to a distant coast which he first makes on an over-sea voyage; and the deficiency of its divergence, whether horizontal or vertical, is not practically felt as an inconvenience in lights of that character, which seldom require to serve the double purpose of being visible at a great distance, and at the same time of acting as guides for dangers near the shore. For such purposes, the lens applies the light much more economically[309] than the reflector, because, while the duration of its least divergent beam is nearly equal to that of the reflector, it is eight times more powerful. A revolving system of eight lenses illuminates an horizontal arc of 32° with this bright beam. The reflector, on the other hand, spreads the light over a larger arc of the horizon; and, while its least divergent beam is much less powerful than that of the lens, the light which is shed over its extreme arc is so feeble as to be practically of little use in lights of extensive range, even during clear weather. When a lighthouse is placed on a very high headland, however, the deficiency of divergence in the vertical direction is often found to be productive of some practical inconvenience; but this defect may be partially remedied by giving to the lenses a slight inclination outwards from the vertical plane of the focus, so as to cause the most brilliant portion of the emergent beam to reach the visible horizon which is due to the height of the lantern. It may be observed, also, that a lantern at the height of 150 feet, which, taking into account the common height of the observer’s eye at sea, commands a range of upwards of 20 English miles, is sufficient for all the ordinary purposes of the navigator, and that the intermediate space is practically easily illuminated, even to within a mile of the lighthouse, by means of a slight inclination of the subsidiary mirrors, even where the light from the principal part of the apparatus passes over the seaman’s head. For the purpose of leading lights, in narrow channels, on the other hand, and for the illumination of certain narrow seas, there can be no doubt that reflectors are much more suitable and convenient. In such cases, the amount of vertical divergence below the horizon, forms an important element in the question, because it is absolutely necessary that the mariner should keep sight of the lights even when he is very near them; while there is not the same call for a very powerful beam which exists in the case of sea-lights. Yet even in narrow seas, where low towers, corresponding to the extent of the range of the light, are used, but where it is, at the same time, needful to illuminate the[310] whole or the greater part of the horizon, the use of dioptric instruments will be found almost unavoidable, especially in fixed lights, as well from their equalizing the distribution of the light in every azimuth, as from their much greater economy in situations where a large annual expenditure would often be disproportionate to the revenue at disposal. In such places, where certain peculiarities of the situation require the combination of a light equally diffused over the greater portion of the horizon, along with a greater vertical divergence in certain azimuths, than dioptric instruments afford, I have found it convenient and economical to add to the fixed refracting apparatus a single paraboloïdal reflector, in order to produce the desired effect, instead of adapting the whole light to the more expensive plan for the sake of meeting the wants of a single narrow sector of its range. In other cases, where the whole horizon is to be illuminated, and great vertical divergence is at the same time desirable, a slight elevation of the burner, at the expense, no doubt, of a small loss of light, is sometimes resorted to, and is found to produce, with good effect, the requisite depression of the emergent rays.
In certain situations, where a great range and, consequently, a powerful light must be combined with tolerably powerful illumination in the immediate vicinity of the lighthouse, we might, perhaps, advantageously adopt a variation of the form and dimensions of the mirrors employed, so as to resemble those formerly employed at the Tour de Corduan, which were of considerably larger surface and longer focal distance than those which are used in Britain. If such a form were adopted, the power of the light for the purpose of the distant range would be increased; and I would propose to compensate for the deficiency of divergence consequent on a long focal distance, by placing a second burner in some position between the parameter and the vertex, and slightly elevated above the axis of the instrument, so as to throw the greater portion of the beam resulting from this second burner below the horizontal plane of the focus. Such an expedient is no doubt somewhat[311] clumsy and would at the same time involve the consumption of twice the quantity of oil used in an ordinary catoptric light; but I can still conceive it to be preferable, in certain situations, to the use of lenses alone.
Thus it appears that we must not too absolutely conclude against one, or in favour of the other mode of illumination for lighthouses; but, as in every other department of the arts, we shall find the necessity of patiently weighing all the circumstances of each particular case that comes before us, before selecting that instrument, or combination of instruments, which appears most suitable.
Distinctions of the Dioptric Lights, and the application of coloured media. The mode of distinguishing lights in the system of Fresnel, depends more upon their magnitude and the measured interval of the time of their revolution, than upon their appearance; and no other very marked distinctions, except Fixed and Revolving, have been successfully attempted in France. As above stated, I consider the distinction of the fixed light varied by flashes, to possess an appearance too slightly differing from that of a revolving light, to admit of its being safely adopted in situations where revolving lights are near. The trial which I made at the Little Ross, in the Solway Frith, of producing, by means of lenses, a light flashing once in five seconds of time, although successful so far as mere distinction is concerned, has several practical defects, arising from the shortness of the duration of the flashes, compared with the powerful effect of the fixed part of the apparatus, which I consider sufficient to prevent its adoption in future, especially considering that a much more marked appearance can be produced, by means of reflectors, as has been done at the Buchanness in Aberdeenshire, and the Rhinns of Islay in Argyllshire. Coloured media have never, so far as I know, been applied to Dioptric apparatus, except in the case of the Maplin Light at the mouth of the Thames, and Cromarty Point Light at the entrance to the Cromarty Frith, and in both instances successfully. The enormous loss of light, however, amounting to no less than 0·80 of the whole incident rays, forms a great bar to the adoption of colour as a distinction; and any means which could[312] tend to lessen that absorption, and at the same time produce the characteristic appearance, would be most valuable. I have tried some glasses of a pink tinge, prepared by M. Letourneau of Paris, whose absorption does not exceed 0·57 of the incident rays; but the appearance of the light, at a distance, is much less marked than that produced by the glasses used in Britain.[77] Such deficiency of characteristic colour might lead to serious consequences, as the transmission of white rays, through a hazy atmosphere, too often produces, by absorption, a reddish tinge of the light, for which the less marked appearance given by the paler media might be easily mistaken. This colouring power of absorption is so well known, that red lights are seldom used except in direct contrast with white ones; but, on a coast so thickly studded with Lighthouses as that of Britain, the number of distinctions is insufficient to supply all our wants, so that we are sometimes reluctantly compelled to adopt a single red light in some situation of lesser importance, or which, from some local circumstances and the appearance of the lights which must be seen by the mariner before passing it, is not likely to be mistaken. The great loss of light by coloured media causes the red beam, in a revolving light, to be seen at a shorter distance than the white; and it is conceivable that, in certain circumstances, this might lead the mariner to mistake a red and white light for a white light revolving at half the velocity. Such a mistake might perhaps prove dangerous; but the lights are generally so situated that there is ample time for the mariner, after first discovering the red light, and thus correcting any mistake, to shape his course accordingly. All other coloured media except red have been found useless as distinctions for any lights of extensive range, and fail to be efficient, owing to the necessity of absorbing almost all the light before a marked appearance can be obtained. In a few pier or ferry lights, green and blue media have been tried, and found available at the distance of a few cables’ lengths.
[313]
It seems to be a natural consequence of the physical distribution of light, that fixed lights, which illuminate the whole horizon, should be less powerful than revolving lights which have their effect concentrated within narrow sectors of the horizon. Any attempt to increase the power of fixed lights is, therefore, worthy of attention; Captain Basil Hall’s proposal for producing the appearance of Fixed Lights by rapid movement. and when the late Captain Basil Hall proposed a plan for effecting this object, it received, as it deserved, the full consideration of the Lighthouse Board, who authorised me to repeat Captain Hall’s experiments, and verify his results by observations made at a considerable distance. As some interesting phenomena of irradiation were evolved in the course of those trials, I think it right to give some account of the results which were obtained, as they bear upon various questions connected with the practical arrangements of Lighthouses, under certain circumstances.
In revolving lights on the dioptric principle, the annular lens of Fresnel, as formerly stated, is employed. This instrument, as the reader already knows, possesses the property of projecting to the horizon, in the form of one pencil or beam, all the light which falls on its inner surface from a lamp placed in its principal focus. The consequence of this action is, that when several lenses are so arranged as to form a right prism which circulates round a lamp placed in the common focus, a distant observer receives from each lens, as its axis crosses his line of vision, a bright flash, which is succeeded by total darkness, when one of the dark spaces intermediate between the lenses passes over his eye; and this succession of bright flashes alternating with dark intervals, produces the characteristic appearance of a revolving light.
The fixed light, on the other hand, presents to the eye a steady and unchanging appearance; and the chief object to be obtained in its construction, is to unite the greatest brilliancy with an equal distribution of the light in every direction. The condition of perfect distribution, as already said, is most rigorously fulfilled by the use of refracting zones or belts, which form, by their union, a cylinder enveloping the flame placed in its centre, and possess the property of refracting the light in the vertical direction only, without[314] affecting its natural divergence horizontally. The light from the focus which is incident on the inner surface of the belt is therefore projected forwards in the shape of a flat ring of equal brilliancy all round the horizon.
This repetition may seem needless, but it is hoped it will be found useful in rendering intelligible the following outline of the plan proposed by Captain Hall for the improvement of fixed lights, and the account of the trials that were made with that object in view.
The familiar experiment of whirling a burning stick quickly round the head, so as to produce a ribbon of light, proves the possibility of causing a continuous impression on the retina by intermittent images succeeding each other with a certain rapidity. From the moderate velocity at which this continuity of impression is obtained, we should be warranted in concluding, a priori, that the time required to make an impression on the retina is considerably less than the duration of the impression itself; for the continuity of effect must, of course, be caused by fresh impulses succeeding each other before the preceding ones have entirely faded. If it were otherwise, and the time required to make the impression were equal to the duration of the sensation, it would obviously be impossible to obtain a series of impulses so close or continuous in their effects as to run into and overlap each other, and thus throw out the intervals of darkness; because the same velocity which would tend to shorten the dark intervals, would also curtail the bright flashes, and thus prevent their acting on the eye long enough to cause an impression. Accordingly, we find that the duration of an impression is in reality much greater than the time required for producing the effect on the retina. It is stated by Professor Wheatstone, in the London Transactions for 1834, that only about one millionth part of a second is required for making a distinct impression on the eye; and it appears, from a statement made by Lamé, at p. 425 of his Cours de Physique, that M. Plateau found that an impression on the retina preserved its intensity unabated during one hundredth of a second, so that, however small those[315] times may be in themselves, the one is yet 10,000 greater than the other.
It has been ascertained by direct experiment,[78] that the eye can receive a fresh impression before the preceding one has faded; and, indeed, if this were impossible, absolute continuity of impression from any succession of impulses, however rapid, would seem to be unattainable; and the approach to perfect continuity would be inversely as the time required to make an impression.
[78] Lamé, Cours de Physique, p. 424. “L’impression peut subsister encore lorsque la suivante a lieu.”
Effects of rapid motion on the power of Lights. From this property which bright bodies passing rapidly before the eye possess of communicating a continuous impression to the sense of sight, Captain Hall conceived the idea, not merely of obtaining all the effects of a fixed light, by causing a system of lenses to revolve with such a velocity as to produce a continuous impression, but, at the same time, of obtaining a much more brilliant appearance, by the compensating influence of the bright flashes, which he expected would produce impulses sufficiently powerful and durable to make the deficiency of light in the dark spaces almost imperceptible. The mean effect of the whole series of changes would, he imagined, be thus greatly superior to that which can be obtained from the same quantity of light equally distributed, as in fixed lights, over the whole horizon. Now this expectation, if it be considered solely in reference to the physical distribution of the light, involves various difficulties. The quantity of light subjected to instrumental action is the same whether we employ the refracting zones at present used in fixed dioptric lights, or attempt to obtain continuity of effect by the rapid revolution of lenses; and the only difference in the action of those two arrangements is this, that while the zones distribute the light equally over the whole horizon, or rather do not interfere with its natural horizontal distribution, the effect of the proposed method is to collect the light into pencils, which are made to revolve with such rapidity, that the impression from each pencil succeeds the preceding one in time to prevent a sensible occurrence of darkness. To expect that the mean effect of[316] the light, so applied, should be greater than when it is left to its natural horizontal divergence, certainly appears at first to involve something approaching to a contradiction of physical laws. In both cases, the same quantity of light is acted upon by the instrument; and in either case, any one observer will receive an impression similar and equal to that received by any other stationed at a different part of the horizon; so that, unless we imagine that there is some loss of light peculiar to one of the methods, we are, in the physical view of the question, shut up to the conclusion, that the impressions received by each class of observers must be of equal intensity. In other words, the same quantity of light is by both methods employed to convey a continuous impression to the senses of spectators in every direction, and in both methods equality of distribution is effected, since it does not at all consist with our hypothesis, that any one observer in the same class should receive more or less than his equal share of the light. Then, as to the probability of the loss of light, it seems natural to expect that this should occur in connection with the revolving system, because the velocity is an extraneous circumstance, by no means necessary to an equal distribution of the light, which can, as we already know, be more naturally and at the same time perfectly, attained by the use of the zones.
On the other hand, it must not be forgotten, that although the effect of both methods is to give each part of the horizon an equal share of light, there is yet this difference between them, that while the light from the zones is equally intense at every instant of time, that evolved by the rapidly circulating lenses is constantly passing through every phase between total darkness and the brightest flash of the lens; and this difference, taken in connection with some curious physiological observations regarding the sensibility of the retina, gives considerable countenance to the expectation on which Captain Hall’s ingenious expedient is based. The fact which has already been noticed, and which the beautiful experiments of M. Plateau and Professor Wheatstone have of late rendered more precise, that the duration of an impression on the retina is not only[317] appreciable, but is much greater than the time required to cause it, seems to encourage us in expecting, that while the velocity required to produce continuity of effect would not be found so great as to interfere with the formation of a full impression, the duration of the impulse from each flash would remain unaltered, and the dark intervals which do not excite the retina would, at the same time, be shortened, and that, therefore, we might in this manner obtain an effect on the senses exceeding the brilliancy of a steady light distributed equally in every direction by the ordinary method. Some persons, indeed, who have speculated on this subject, seem even to be of opinion, that, so far from the whole effect of the series of continuous impressions being weakened by a blending of the dark with the bright intervals, the eye would in reality be stimulated by the contrast of light and darkness, so as thereby to receive a more complete and durable impulse from the light. It is obvious, however, that this question regarding the probable effect to be anticipated from a revolution so rapid as to cause a continuous impression, could only have been satisfactorily answered by an appeal to experiment.
In experimenting on this subject, I used the apparatus formerly employed by Captain Hall. It consisted of an octagonal frame, which carried eight of the discs that compose the central part of Fresnel’s compound lens, and was susceptible of being revolved slowly or quickly at pleasure, by means of a crank-handle and some intermediate gearing. The experiments were nearly identical with those made by Captain Hall, who contrasted the effect of a single lens at rest, or moving very slowly, with that produced by the eight lenses, revolving with such velocity as to cause an apparently continuous impression on the eye. To this experiment I added that of comparing the beam thrown out by the central portion of a cylindric refractor, such as is used at the fixed light of the Isle of May, with the continuous impression obtained by the rapid revolution of the lenses. Captain Hall made all his comparisons at the short distance of 100 yards; and in order to obtain[318] some measure of the intensity, he viewed the lights through plates of coloured glass until the luminous discs became invisible to the eye. I repeated those experiments at Gullan, under similar circumstances, but with very different results. I shall not, however, enter upon the discussion of those differences here, although they are susceptible of explanation, and are corroborative of the conclusions at which I arrived, by comparing the lights from a distance of 14 miles; but shall briefly notice the more important results which were obtained by the distant view. They are as follows:—
1. The flash of the lens revolving slowly was very much larger than that of the rapidly revolving series; and this decrease of size in the luminous object presented to the eye, became more marked as the rate of revolution was accelerated, so that, at the velocity of eight or ten flashes in a second, the naked eye could hardly detect it, and only a few of the observers saw it; while the steady light from the fixed refractor was distinctly visible.
2. There was also a marked falling off in the brilliancy of the rapid flashes as compared with that of the slow ones; but this effect was by no means so striking as the decrease of volume.
3. Continuity of impression was not attained at the rate of five flashes in a second, but each flash appeared to be distinctly separated by an interval of darkness; and even when the nearest approach to continuity was made, by the recurrence of eight or ten flashes in a second, the light still presented a twinkling appearance, which was well contrasted with the steady and unchanging effect of the cylindric refractor.
4. The light of the cylindric refractor was, as already stated, steady and unchanging, and of much larger volume than the rapidly revolving flashes. It did not, however, appear so brilliant as the flashes of the quickly revolving lenses, more especially at the lower rate of five flashes in a second.
5. When viewed through a telescope, the difference of volume between the light of the cylindric refractor and that produced by[319] the lenses at their greatest velocity was very striking. The former presented a large diffuse object of inferior brilliancy, while the latter exhibited a sharp pin-point of brilliant light.
Upon a careful consideration of these facts it appears warrantable to draw the following general conclusions:—
1. That our expectations as to the effects of light, when distributed according to the law of its natural horizontal divergence, are supported by observed facts as to the visibility of such lights, contrasted with those whose continuity of effect is produced by collecting the whole light into bright pencils, and causing them to revolve with great velocity.
2. It appears that this deficiency of visibility seems to be chiefly due to a want of volume in the luminous object, and also, although in a less degree, to a loss of intensity, both of which defects appear to increase in proportion as the motion of the luminous object is accelerated.
3. That this deficiency of volume is the most remarkable optical phenomenon connected with the rapid motion of luminous bodies, and that it appears to be directly proportional to the velocity of their passage over the eye.
4. That there is reason to suspect that the visibility of distant lights depends on the volume of the impression in a greater degree than has perhaps been generally imagined.
5. That, as the size and intensity of the radiants causing these various impressions to a distant observer were the same, the volume of the light and, consequently, cæteris paribus, its visibility, are, within certain limits, proportionate to the time during which the object is present to the eye.
Such appear to be the general conclusions which those experiments warrant us in drawing; and the practical result, in so far as lighthouses are concerned, is sufficient to discourage us from attempting to improve the visibility of fixed lights in the manner proposed by Captain Hall, even supposing the practical difficulties connected with the great centrifugal force generated by the rapid revolution of the lenses to be less than they really are.
[320]
Connection of the experiments with Irradiation. This decrease in the volume of the luminous object caused by the rapid motion of the lights is interesting, from its apparent connection with the curious phenomenon of irradiation. When luminous bodies, such as the lights of distant lamps, are seen by night, they appear much larger than they would do by day; and this effect is said to be produced by irradiation. M. Plateau, in his elaborate essay on this subject, after a careful examination of all the theories of irradiation, states it to be his opinion, that the most probable mode of accounting for the various observed phenomena of irradiation is to suppose, that, in the case of a night-view, the excitement caused by light is propagated over the retina beyond the limits of the day-image of the object, owing to the increased stimulus produced by the contrast of light and darkness; and he also lays it down as a law confirmed by numerous experiments, that irradiation increases with the duration of the observation. It appears, therefore, not unreasonable to conjecture, that the deficiency of volume observed during the rapid revolution of the lenses may have been caused by the light being present to the eye so short a time, that the retina was not stimulated in a degree sufficient to produce the amount of irradiation required for causing a large visual object. When, indeed, the statement of M. Plateau, that irradiation is proportional to the duration of the observation, is taken in connection with the observed fact, that the volume of the light decreased as the motion of the lenses was accelerated, it seems almost impossible to avoid connecting together the two phenomena as cause and effect.
In the course of supplying the numerous wants of navigation, it will often be found necessary to cut off, on a given bearing, the beam proceeding from a Lighthouse, as a guide to the seaman to avoid some shoal, or as a hint to put about and seek the opposite side of a channel. This is attended with some little practical difficulty,[321] especially in lights from reflectors arranged externally on a circle, because a certain portion of light, chiefly due to the divergence caused by the size of the flames, and partly from the effects of the diffraction or inflexion of the light, spreads faintly over a narrow sector between the light arc and the dark one. Masking Lights. It becomes necessary, of course, to make allowance for this penumbral arc by increasing the masked portion of the lantern; and, where a very sharp line of demarcation is required, a board is sometimes placed on the outside of the Lightroom, in such a position, and of such length, that while it does not enter the boundaries of the luminous sector, it prevents the more powerful part of the penumbral beam from reaching the observer’s eye. This effect is, of course, more conveniently produced, where the circumstances admit of its adoption, by distributing the reflectors round the concave side of the lantern, towards the land; but such an arrangement is inapplicable when the illuminated sector exceeds the dark one. I have found, by observation, that the sector intercepted between the azimuth on which the lantern is masked and that on which total darkness is produced to an observer, at moderate distances, may be estimated at not less than 3° for dioptric, and 7° for catoptric lights of the highest class.[79]
[79] The method which I adopted for determining those quantities, was to mask a certain portion of the lantern of a lighthouse subtending an horizontal sector of about 30° or 40°, and at night to fix, by actual observation, at the distance of 5 or 6 miles, two points on the coast between which the light so masked was obscured. The angle included between the lines joining those points and the centre of the lantern was then determined by triangulation next day, and half the difference between the observed angle (which is always the lesser of the two) and the computed subtense of the masked sector of the lantern, is, in each case, the amount of the allowance stated in the text.
Those quantities may therefore serve to guide the Lighthouse engineer to approximate more rapidly to his object, as he will generally be safe in increasing the dark sector, by one or other of the above constants, according to the kind of apparatus employed. I need not add, that in a matter of this kind, a final appeal to actual observation is, in all cases, indispensable.
[322]
A few words on the subject of double lights, naturally spring out of what has been said about the masking of lights. Double Lights. The term double lights is properly and distinctly confined to lights on different levels, but not necessarily (as leading-lights are) in separate towers. The sole object of using double lights is for distinction from neighbouring lights; and they are unquestionably most effective in this respect, when they are placed in the same tower. In this point of view, therefore, I shall speak of them; and it is obvious that all that peculiarly belongs to them is, that the difference of level between them shall be sufficiently great to present the lights as separate objects to the eye of the seaman, when placed at the greatest distance at which it may be desirable that he should be able to recognise their characteristic appearance. In many cases it is not necessary (but it is certainly always desirable) that the lights should, from the first moment of their being seen, be known as double lights; but in others, it may well consist with safety, that two lights, which appear as a single light when first seen at the distance of 20 miles, shall at 15 or 10 miles distance be discovered to be double. Now we should at first be apt hastily to imagine, that all that is required to produce that effect, is to raise the one light above the other to such an extent, that the distance between them shall be somewhat more than a minimum visibile at the most distant point of observation, or, in other words, that the difference of the height of the lights should be such as to subtend to the eye at the point of observation, an angle greater than 13″·02, which is the subtense of a minimum visibile during the day.[80] But the effect of irradiation, to which I have already alluded, tends to blend together the images of the lights long before their distance apart has become so low a fraction of the observer’s[323] distance from the Lighthouse, as to subtend so small an angle; and I have accordingly found by experiments, conducted under various circumstances, and at various distances, that repeated observations gave me 3′ 18″ as the mean of the subtenses calculated in reference to the distances at which the lights began to be blended into one.
[80] This quantity is deduced from observations made by my friend Mr James Gardner, while engaged on the Ordnance Survey, and may be regarded as the extreme limit of visibility, under the most favourable circumstances as to the state of the atmosphere and also the contrast of colours. The observed object, also, was a pole, not a round disc; and it is familiar to every one accustomed to view distant objects, that vertical length is an important constituent in their visibility.
Adopting this as the smallest angle which the two lights should subtend at the observer’s eye, we may find the least vertical distance between them which will cause them to appear as separate objects by the following formula:
H = 2 Δ . tan θ
in which Δ is the observer’s distance in feet; θ, half the subtense, = 1′ 39″; and H the required height of the tower between the two lights in feet. The following Table gives the height in feet corresponding to the distance in nautic miles, from 1 to 20 inclusive: the heights, which are the bases of similar isosceles triangles, increase, of course, in an arithmetical series:
| Distance of the observer in Nautic Miles. |
Vertical distance in feet between the Lights. |
Distance of the observer in Nautic Miles. |
Vertical distance in feet between the Lights. |
|---|---|---|---|
| 1 | 6·02 | 11 | 66·22 |
| 2 | 12·04 | 12 | 72·24 |
| 3 | 18·06 | 13 | 78·26 |
| 4 | 24·08 | 14 | 84·28 |
| 5 | 30·10 | 15 | 90·30 |
| 6 | 36·12 | 16 | 96·32 |
| 7 | 42·14 | 17 | 102·34 |
| 8 | 48·16 | 18 | 108·36 |
| 9 | 54·18 | 19 | 114·38 |
| 10 | 60·20 | 20 | 120·40 |
Akin to the subject of Double Lights, is that of Leading Lights. Leading Lights,[324] the object of which is to indicate to the mariner a given line of direction by their being seen in one line. In most instances, this line of direction is used to point out the central part of a narrow channel; and the alternate opening of the lights, on either side of their conjunction, serves to indicate to the mariner (who ought to conjoin with his watching of the lights the observation of the elapsed time and also frequent soundings) the proper moment for changing his tack. In some places, the line of conjunction of the lights is placed nearer to one side of a channel than the other, according as the set of the tides, or the position of shoals, may seem to require. In other situations, this line only serves as a cross-bearing to shew the mariner his approach to some danger, or to indicate his having passed it, and thus to assure him of his entry on wider sea-room. Similar considerations to those which determine the difference of elevation for double lights regulate the choice of the distance between two leading lights; but the question is less narrow, and may be generally solved graphically by simply drawing the lines on an accurate chart of the locality. In some few situations, the configuration of the coast does not admit of a separation between the lights, sufficient to cause what is called a sharp intersection; but, in most cases, there is room enough to place them so far apart, that but a few yards of deviation in the vessel’s course, from the exact line of the conjunction of the lights in one, produces a distinct opening between them on the opposite side of that line. In order to insure the requisite sharpness of intersection, the distance between the lights, wherever attainable, should be not less than one-sixth of the distance between the more seaward of the two Towers and that point at which the seaman begins to use the line of conjunction as his guide. I have only to add, that in situations where the land prevents a considerable separation between leading lights, they should be placed as nearly on one level as is consistent with their being seen as vertically separated, so as in some measure to compensate for their horizontal nearness, by rendering their intersection more sharp and striking[325] than it can be where the observer must draw from the upper light an imaginary perpendicular in his mind, and then estimate the separation of the lights by the sine of an angle, which decreases as the difference of their apparent elevations increases.
Distribution of Lights on a Coast. The considerations which enter into the choice of the position and character of the Lights on a line of coast, are either, on the one hand, so simple and self-evident as scarcely to admit of being stated in a general form, without becoming mere truisms; or are, on the other hand, so very numerous and often so complicated as scarcely to be susceptible of compression into any general laws. I shall not, therefore, do more than very briefly allude to a few of the chief considerations which should guide us in the selection of the sites and characteristic appearance of the Lighthouses to be placed on a line of coast. Perhaps those views may be most conveniently stated in the form of distinct propositions:—
1. The most prominent points of a line of coast, or those first made on over-sea voyages, should be first lighted; and the most powerful lights should be adapted to them, so that they may be discovered by the mariner as long as possible before his reaching land.
2. So far as is consistent with a due attention to distinction, revolving lights of some description, which are necessarily more powerful than fixed lights, should be employed at the outposts on a line of coast.
3. Lights of precisely identical character and appearance should not, if possible, occur within a less distance than 100 miles of each other on the same line of coast, which is made by over-sea vessels.
4. In all cases, the distinction of colour should never be adopted except from absolute necessity.
5. Fixed lights and others of less power, may be more readily adopted in narrow seas, because the range of the lights in such situations is generally less than that of open sea-lights.
6. In narrow seas also, the distance between lights of the same appearance may often be safely reduced within much lower limits than is desirable for the greater sea-lights; and there are many instances in which the distance separating lights of the same character[326] need not exceed 50 miles, and there are peculiar cases in which even a much less separation between similar lights may be sufficient.
7. Lights intended to guard vessels from reefs, shoals, or other dangers, should in every case be placed, where practicable, to the seaward of the danger itself, as it is desirable that seamen be enabled to make the lights with confidence.
8. Views of economy in the first cost of a Lighthouse should never be permitted to interfere with placing it in the best possible position; and, when funds are deficient, it will generally be found that the wisest course is to delay the work until a sum shall have been obtained sufficient for the erection of the lighthouse on the best site.
9. The elevation of the lantern above the sea should not, if possible, for sea-lights, exceed 200 feet; and about 150 feet is sufficient, under almost any circumstances, to give the range which is required. Lights placed on high headlands are subject to be frequently wrapped in fog, and are often thereby rendered useless, at times when lights on a lower level might be perfectly efficient. But this rule must not, and indeed cannot, be strictly followed, especially on the British coast, where there are so many projecting cliffs, which, while they subject the lights placed on them to occasional obscuration by fog, would also entirely and permanently hide from view lights placed on the lower land adjoining them. In such cases, all that can be done is carefully to weigh all the circumstances of the locality, and choose that site for the lighthouse which seems to afford the greatest balance of advantage to navigation. As might be expected, in questions of this kind, the opinions of the most experienced persons are often very conflicting, according to the value which is set on the various elements which enter into the inquiry.
10. The best position for a sea-light ought rarely to be neglected for the sake of some neighbouring port, however important or influential; and the interests of navigation, as well as the true welfare of the port itself, will generally be much better served by placing the sea-light where it ought to be, and adding, on a smaller[327] scale, such subsidiary lights as the channel leading to the entrance of the port may require.
11. It may be held as a general maxim, that the fewer lights that can be employed in the illumination of a coast the better, not only on the score of economy, but also of real efficiency. Every light needlessly erected may, in certain circumstances, become a source of confusion to the mariner, and, in the event of another light being required in the neighbourhood, it becomes a deduction from the means of distinguishing it from the lights which existed previous to its establishment. By the needless erection of a new Lighthouse, therefore, we not only expend public treasure, but waste the means of distinction among the neighbouring lights.
12. Distinctions of lights, founded upon the minute estimation of intervals of time between flashes, and especially on the measurement of the duration of light and dark periods, are less satisfactory to the great majority of coasting seamen, and are more liable to derangement by atmospheric changes, than those distinctions which are founded on what may more properly be called the characteristic appearance of the lights, in which the times for the recurrence of certain appearances differ so widely from each other as not to require for their detection any very minute observation in a stormy night. Thus, for example, flashing lights of five seconds interval, and revolving lights of half a minute, one minute, and two minutes, are much more characteristic than those which are distinguished from each other by intervals varying according to a slower series of 5″, 10″, 20″, 40″, &c.
13. Harbour and local lights, which have a circumscribed range, should generally be fixed instead of revolving; and may often, for the same reason, be safely distinguished by coloured media. In many cases also, where the purpose of guiding into a narrow channel is to be gained, the leading lights which are used, should, at the same time, be so arranged as to serve for a distinction from any neighbouring lights.
14. Floating lights, which are very expensive and more or less uncertain from their liability to drift from their moorings, as well[328] as defective in power, should never be employed to indicate a turning point in a navigation in any situation where the conjunction of lights on the shore can be applied at any reasonable expense.
Height of Lighthouse Tower, and its relation to range of Light. The spheroïdal form of the Earth requires that the height of a Lighthouse Tower should increase proportionally to the difference between the Earth’s radius and the secant of the angle intercepted between the normal to the spheroïd at the Lighthouse and the normal at the point of the light’s occultation from the view of a distant observer. The effect of atmospheric refraction, however, is too considerable to be neglected in estimating the range of a light, or in computing the height of a Tower which is required to give to any light a given range; and we must, therefore, in accordance with the influence of this element, on the one hand increase the range due to any given height, and vice versa reduce the height required for any given range, which a simple consideration of the form of the globe would assign. In considering this height, we may proceed as follows:—
Fig. 92.
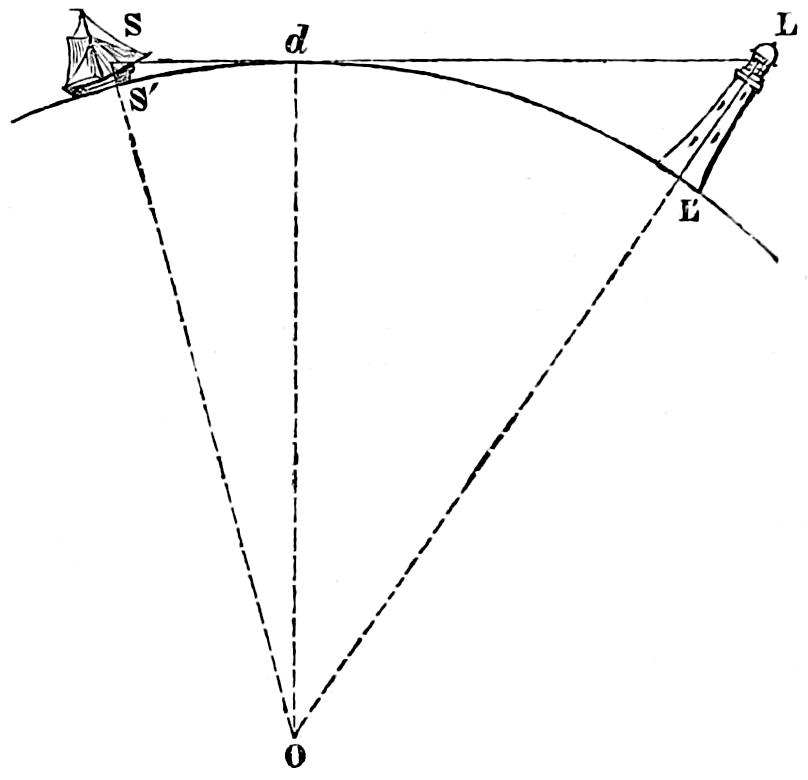
Referring to the accompanying figure (No. 92), in which S′ d L′ is a segment of the ocean’s surface, O the centre of the earth, L′L a Lighthouse, and S the position of the mariner’s eye, we obtain the value of LL′ = H′, the height of the tower in feet by the formula,
H′ = 2 l² 3 (1.)
in which l = the distance in English miles L′d at which the light would strike the ocean’s surface. We then reduce this value of H′ by the correction for mean refraction, which permits the light to be seen at a greater distance, and which =
2 l² 21, (2.)
So as to get, H = 2 l²3 - 2 l²21 = 4 l²7 (3.)
an expression which at once gives the height of the tower required,[329] if the eye of the mariner were just on the surface of the water at d, where the tangent between his eye at S and the light at L would touch the sea. We must, therefore, in the first instance, find the distance d S = l′, which is the radius of the visible horizon due to the height SS′ = h of his eye above the water, and is, of course, at once obtained conversely by the expression:—
l′ = √7 h 2 (4.)
Deducting this distance from SL, the whole effective range of the light, we have L d = l, and operating with this value in the former equation,
H = 4 l²7
we find the height of the tower which answers the conditions of the case.[81] From the above data the following Table has been computed.
[81] In the above expressions l and l′ are given in English miles, which in Scotland may be considered as bearing to nautical miles the ratio of 5280 to 6088. In order to convert a distance given in nautical miles to English miles, all that is needful is to add the log of the number of nautical miles to log 5280, and subtract log 6088.
| H | λ | λ′ | H | λ | λ′ | H | λ | λ′ |
|---|---|---|---|---|---|---|---|---|
| Heights in Feet. |
Lengths in English Miles. |
Lengths in Nautical Miles. |
Heights in Feet. |
Lengths in English Miles. |
Lengths in Nautical Miles. |
Heights in Feet. |
Lengths in English Miles. |
Lengths in Nautical Miles. |
| 5 | 2·958 | 2·565 | 70 | 11·067 | 9·598 | 250 | 20·916 | 18·14 |
| 10 | 4·184 | 3·628 | 75 | 11·456 | 9·935 | 300 | 22·912 | 19·87 |
| 15 | 5·123 | 4·443 | 80 | 11·832 | 10·26 | 350 | 24·748 | 21·46 |
| 20 | 5·916 | 5·130 | 85 | 12·196 | 10·57 | 400 | 26·457 | 22·94 |
| 25 | 6·614 | 5·736 | 90 | 12·549 | 10·88 | 450 | 28·062 | 24·33 |
| 30 | 7·245 | 6·283 | 95 | 12·893 | 11·18 | 500 | 29·580 | 25·65 |
| 35 | 7·826 | 6·787 | 100 | 13·228 | 11·47 | 550 | 31·024 | 26·90 |
| 40 | 8·366 | 7·255 | 110 | 13·874 | 12·03 | 600 | 32·403 | 28·10 |
| 45 | 8·874 | 7·696 | 120 | 14·490 | 12·56 | 650 | 33·726 | 29·25 |
| 50 | 9·354 | 8·112 | 130 | 15·083 | 13·08 | 700 | 35·000 | 30·28 |
| 55 | 9·811 | 8·509 | 140 | 15·652 | 13·57 | 800 | 37·416 | 32·45 |
| 60 | 10·246 | 8·886 | 150 | 17·201 | 14·91 | 900 | 39·836 | 34·54 |
| 65 | 10·665 | 9·249 | 200 | 18·708 | 16·22 | 1000 | 41·833 | 36·28 |
[330]
If the distance at which a light of given height can be seen by a person on a given level be required, it is only needful to add together the two numbers in the column of lengths λ or λ′ (according as Nautical or English miles may be sought) corresponding to those in the column of heights H, which represent respectively the height of the observer’s eye and the height of the lantern above the sea. When the height required to render a light visible at a given distance is required, we must seek first for the number in λ or λ′ corresponding to the height of the observer’s eye, and deduct this from the whole proposed range of the light, and opposite the remainder in λ or λ′ seek for the corresponding number in H.
A considerable practical defect in all the lighthouse lanterns which I have ever seen, with the exception of those recently constructed for the Scotch Lighthouses, consists in the vertical direction of the astragals, which, of course, tend to intercept the whole or a great part of the light in the azimuth which they subtend.[82] The consideration of the improvement which I had effected in giving a Diagonal Lantern. diagonal direction to the joints of the fixed refractors, first led me (as stated at p. 266, ante), to adopt a diagonal arrangement of the framework which carries the cupola of zones and afterwards for the astragals of the lantern. Not only is this direction of the astragals more advantageous for equalising the effect of the light; but the greater stiffness and strength which this arrangement gives to the frame-work of the lantern make it safe to use more slender bars and thus also absolutely less light is intercepted. The panes of glass at the same time become triangular, and are necessarily stronger than rectangular panes of equal surface. This form of lantern is extremely light and elegant, and is shewn, with detailed drawings of some of its principal parts, in Plate XXVI. To avoid the necessity of painting, which, in situations so exposed as those which lighthouses generally occupy, is attended with many inconveniences and no small risk, the framework of the lantern is now formed of gun-metal and the dome is of copper; so that a first[331] order lantern of 12 feet diameter and 10 feet height of glass costs, when glazed, about L.1260. In order to give the lightkeepers free access to cleanse and wash the upper panes of the lantern (an operation which in snowy weather must sometimes be frequently repeated during the night), a narrow gangway, on which they may safely stand, is placed on the level of the top of the lower panes, and at the top of the second panes, rings are provided of which the lightkeepers may lay hold for security in stormy weather. A light trap-ladder is also attached to the outside of the lantern by means of which there is an easy access to the ventilator on the dome.
[82] I must also except the small pier light at Kirkcaldy, erected (I believe in 1836) by my friend Mr Edward Sang.
Glazing of the Lantern. Great care is bestowed on the glazing of the lantern, in order that it may be quite impervious to water, even during the heaviest gales. When iron is used for the frames, they are carefully and frequently painted; but gun-metal, as just noticed, is now generally used in the Scotch Lighthouses. There is great risk of the glass plates being broken by the shaking of the lantern during high winds; and as much as possible to prevent this, various precautions are adopted. The arris of each plate is always carefully rounded by grinding; and grooves about ¹⁄₂ inch wide, capable of holding a good thickness of putty, are provided in the astragals for receiving the glass, which is ¹⁄₄ inch thick. Small pieces of lead or wood are inserted between the frames and the plates of glass against which they may press, and by which they are completely separated from the more unyielding material of which the lantern-frames are composed. Panes glazed in frames padded with cushions, and capable of being temporarily fixed in a few minutes, in the room of a broken plate, are kept ready for use in the Store-room. Those framed plates are called storm-panes, and have been found very useful on several occasions, when the glass has been shattered by large sea-birds coming against it in a stormy night, or by small stones violently driven against the lantern by the force of the wind.
Ventilation of the Lanterns. The ventilation of the lanterns forms a most important element in the preservation of a good and efficient light. An ill-ventilated lantern has its sides continually covered with the water of condensation, which is produced by the contact of the ascending current[332] of heated air; and the glass thus obscured obstructs the passage of the rays, and diminishes the power of the light. In the Northern Lighthouses, ventilators, capable of being opened and shut at pleasure, so as to admit from without a supply of air when required, are provided in the parapet-wall on which the lantern stands; the lantern roof also is surmounted by a cover which, while it closes the top of an open cylindric tube against the entrance of rain, and descends over it only so far as is needful for that purpose, still leaves an open air-space between it and the dome. This arrangement permits the current of heated air, which is continually flowing from the lantern through the cylindric tube, to pass between it and the outer cover, from which it finally escapes to the open air through the space between the cover and the dome. The door which communicates from the lightroom through the parapet to the balcony outside, is also made the means of ventilating the lightroom; and, for that purpose, it is provided with a sliding bolt at the bottom, which, being dropped into one or other of the holes cut in the balcony for its reception, serves to keep the door open at any angle that may be found necessary. A useful precaution was introduced by my predecessor, as Engineer to the Northern Lights Board, in order to prevent the too rapid condensation of heated air on the large internal surface of the lantern roof, which consists in having two domes with an air-space between them, as shewn in the enlarged diagrams in Plate XXVI.
An important improvement in the ventilation of Lighthouses was some years ago introduced by Dr Faraday into several of the Lighthouses belonging to the Trinity House, and has since been adopted in all the dioptric lights belonging to the Commissioners of Northern Lighthouses. After mentioning several proofs of extremely bad ventilation in Lighthouses, Dr Faraday thus describes his apparatus:[83]
[83] Minutes of Institution of Civil Engineers, vol. i., p. 207.
“The ventilating pipe or chimney is a copper tube, 4 inches in diameter, not, however, in one length, but divided into three or four pieces; the lower end of each of these pieces for about 1¹⁄₂ inch[333] is opened out into a conical form, about 5¹⁄₂ inches in diameter at the lowest part. When the chimney is put together, the upper end of the bottom piece is inserted about ¹⁄₂ inch into the cone of the next piece above, and fixed there by three ties or pins, so that the two pieces are firmly held together; but there is still plenty of air-way or entrance into the chimney between them. The same arrangement holds good with each succeeding piece. When the ventilating chimney is fixed in its place, it is adjusted so that the lamp-chimney enters about ¹⁄₂ inch into the lower cone, and the top of the ventilating chimney enters into the cowl or head of the lantern.
“With this arrangement, it is found that the action of the ventilating flue is to carry up every portion of the products of combustion into the cowl; none passes by the cone apertures out of the flue into the air of the lantern, but a portion of the air passes from the lantern by these apertures into the flue, and so the lantern itself is in some degree ventilated.
“The important use of these cone apertures is that when a sudden gust or eddy of wind strikes into the cowl of the lantern, it should not have any effect in disturbing or altering the flame. It is found that the wind may blow suddenly in at the cowl, and the effect never reaches the lamp. The upper, or the second, or the third, or even the fourth portion of the ventilating flue might be entirely closed, yet without altering the flame. The cone junctions in no way interfere with the tube in carrying up all the products of combustion; but if any downward current occurs, they dispose of the whole of it into the room without ever affecting the lamp. The ventilating flue is in fact a tube, which, as regards the lamp, can carry everything up but conveys nothing down.”
The advantages of this arrangement, as applied to the Northern Lighthouses, were much less palpable than those which are described in the beginning of Dr Faraday’s paper, because their ventilation was very good before its introduction; and the flame in particular was perfectly steady, being by no means subject to[334] derangement from sudden gusts of wind from the roof in the manner noticed above.
Arrangements and internal management of a Lighthouse. All the Lighthouses in the district of the Commissioners are under the charge of at least two Lightkeepers, whose duties are to cleanse and prepare the apparatus for the night illumination, to mount guard singly after the light is exhibited, and to relieve each other at stated hours, fixed by the printed regulations and instructions, under which they act. The rule is, that no keeper on watch shall, under any circumstances, leave the Lightroom until relieved by his comrade; and, for the purpose of cutting off all pretext for the neglect of this universal law, the dwelling-houses are built close to the Light Tower, and means are provided for making signals directly from the Lightroom to the sleeping apartments below. These signals are communicated by air-tubes, through which, by means of a small piston, or a puff of wind from the mouth, calls can be exchanged between the keepers, enabling the man on guard in the Lightroom, at the end of the watch, or on any sudden emergence, to summon his comrade from below, who, on being thus called, answers by a counter-blast, to shew that the summons has been heard and will be obeyed. For the purpose of greater security, in such situations as the Bell Rock and the Skerryvore, four keepers are provided for one lightroom; one being always ashore on leave with his family, and the other three being at the Lighthouse, so that, in case of the illness of one lightkeeper, an efficient establishment of two keepers for watching the light may remain. At all the land-lighthouses also, an agreement is made with some steady person residing in the neighbourhood, who is instructed in the management of the light and cleansing of the apparatus, and comes under an obligation to be ready to do duty in the light-room when called upon, in the event of the sickness or absence of one of the lightkeepers. This person is called the occasional keeper, and receives pay only while actually employed at the Lighthouse; but in order to keep him in the practice of the duty, he is required to serve in the lightroom for a fortnight annually in the month of January. The details of the lightkeeper’s duty may be seen by referring to[335] the instructions already alluded to, which will be found in the Appendix.
Each of the two lightkeepers has a house for himself and family, both being under a common roof, but entering by separate doors, as shewn in Plates XXVII. and XXVIII., which exhibit the buildings for the new Lighthouse at Ardnamurchan Point, on the coast of Argyllshire. The principal keeper’s house consists of six rooms, two of which are at the disposal of the visiting officers of the Board, whose duty in inspecting the Lighthouse, or superintending repairs, may call them to the station; and the assistant has four rooms, one of which is used as a barrack-room for the workmen, who, under the direction of the Foreman of the lightroom works, execute the annual repairs of the apparatus.
The early Lighthouses contained accommodation for the lightkeepers in the Tower itself; but the dust caused by the cleaning of those rooms in the Tower was found to be very injurious to the delicate apparatus and machinery in the lightroom. Unless, therefore, in situations such as Skerryvore, where it is unavoidable, the dwellings of the lightkeepers ought not to be placed in the Light Tower, but in an adjoining building.
Great care should be bestowed to produce the utmost cleanliness in everything connected with a Lighthouse, the optical apparatus of which is of such a nature as to suffer materially from the effect of dust in injuring its polish. For this purpose covered ash-pits are provided at all the dwelling-houses, in order that the dust of the fire-places may not be carried by the wind to the lightroom; and for similar reasons, iron floors are used for the lightrooms instead of stone, which is often liable to abrasion, and all the stonework near the lantern is regularly painted in oil.
If, in all that belongs to a lighthouse, the greatest cleanliness be desirable, it is in a still higher degree necessary in every part of the lightroom apparatus, without which the optical instruments and the machinery will neither last long nor work well. Cleansing of Apparatus. Every part of the apparatus, whether lenses or reflectors, should be carefully[336] freed from dust before being either washed or burnished; and without such a precaution, the cleansing process would only serve to scratch them. For burnishing the reflectors, prepared rouge (tritoxide of iron) of the finest description, which should be in the state of an impalpable powder of a deep orange-red colour, is applied, by means of soft chamois skins, as occasion may require; but the great art of keeping reflectors clean consists in the daily, patient, and skilful application of manual labour in rubbing the surface of the instrument with a perfectly dry, soft, and clean skin, without rouge. The form of the hollow paraboloid is such, that some practice is necessary in order to acquire a free movement of the hand in rubbing reflectors; and its attainment forms one of the principal lessons in the course of the preliminary instruction, to which candidates for the situation of a light-keeper are subjected at the Bell Rock Lighthouse. For cleansing the lenses and glass mirrors, spirit of wine is used. Having washed the surface of the instrument with a linen cloth steeped in spirit of wine, it is carefully dried with a soft and dry linen rubber, and finally rubbed with a fine chamois skin, free from any dust which would injure the polish of the glass, as well as from grease. It is sometimes necessary to use a little fine rouge with a chamois skin, for restoring any deficiency of polish which may occur from time to time; but in a well-managed lighthouse this application will seldom, if ever, be required.
The machinery of all kinds, whether that of the mechanical lamp or the revolving apparatus, should also be kept scrupulously clean, and all the journals should be carefully oiled.
Mode of measuring the relative intensity and power of Lights. As I have had frequent occasion to speak of the comparative power of lights, it will not be out of place to present the reader with a few practical observations, chiefly drawn from the excellent work of M. Peclet to which I have so often referred, on the measurement of the intensity of lights by the method of shadows.
Fig. 93.
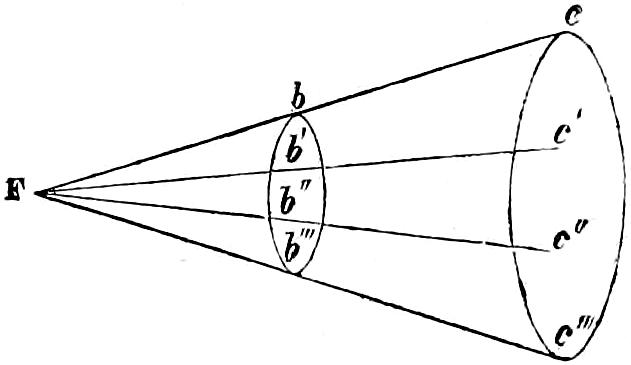
The intensity of light decreases as the observer recedes from the luminous body, in proportion to the square of his distance.[337] Suppose a beam of light to proceed from a radiant at F, and we shall have the rays which, of course, move in straight lines, gradually receding from each other, as b, b′, b″, b‴, and c, c′, c″, c‴, so that the section of the beam will increase with the distances F b, and F c; and the same number of rays, being thus spread over spaces continually increasing, will illuminate the surfaces with a less intensity. This decrease of intensity will, therefore, be in the inverse ratio of the extent of the transverse parallel sections of the luminous cones at b and c, which, we know, increase as the square of their distances from the apex of the cone at F. Hence we conclude, that the intensity of any section of a divergent beam of light decreases as the square of its distance from the radiant. This law furnishes us with a simple measure of the comparative intensity of lights. If we suppose two lights so placed that they may separately illuminate adjacent portions of a vertical screen of paper, we may, by repeatedly comparing the luminousness of those surfaces, and moving one of the lights farther from, or nearer to the screen, at length cause the separate portions of the paper to become equally luminous. This arrangement, however, has many practical difficulties, which I shall not wait to specify; but shall at once indicate a more simple and equally correct mode of obtaining the same result, by means of the shadows cast by the lights from an opaque rod, in a vertical position at O (fig. 94), placed between them, and a screen covered with white paper on which the shadows fall. It is obvious that the light at F would cause the object O to cast a shadow at SS, while the light at F′ would cast a shadow at S′S′. But while the shadow at S would still receive light from F′, S′ would receive light from F, so that those two shadows are, in fact, the only portions of the screen which are each illuminated only by one of the lights, while every other portion[338] of its surface receives light from both the radiants at F and F′. If we suppose F to be the weaker light, we can bring it nearer the screen, until the shadow S′S′, shall become similar in appearance to the shadow SS; and we shall have the ratio of the intensity of the light at F to that of the light at F′, as (FS′)² is to (F′S)², which distances must be measured with the greatest exactness. Such is the mode commonly used in estimating the comparative intensities of two lights; but there are various precautions which are needful in order to prevent errors in comparing the deepness of the shadows, and to insure the greatest attainable accuracy in the estimate of the power of the lights, which I shall endeavour briefly to describe.
Fig. 94.
More accurate comparison of the intensity of Lights. The difficulties of estimating the deepness or sharpness of the shadow is very great, and many persons seem quite incapable of arriving at any right judgment in this matter. The same person also will discover such unaccountable variations in his decision after observations made at short intervals of time, as, one would think, can only arise from a sudden change of the intensity of one or both lights. M. Peclet, in his Traité de l’éclairage, gives, as the result of his experience (and I can fully confirm his result by my own), that those differences depend less frequently on any real difficulty of estimating the deepness of the shadows, than on variations in the position of the observer, or rather in the angle at which he views the shadows, and that, consequently, in proportion to the distance between the two shadows, this source of error is increased. Any thing like a glossy texture of the surface of the screen, which then, of course, becomes a reflector, also tends to aggravate this evil. Thus, if the two lights which are to be compared be placed on a table, in such situations as to spread pretty far apart on the screen the shadows of a vertical rod placed between them; and if the shadow nearer to the observer seem to be a little deeper or sharper than the other, let the observer look at them from the other side of the table, and their difference will be reversed, and that which seemed the paler, will become the deeper. Again, if the difference between the two shadows be very great[339] when seen from the right side of the screen, it may happen that, on viewing them from the left hand, the difference may still be in favour of the same shadow, but in a much less degree.
“When I observed this effect,” says M. Peclet,[84] “I tried to view the shadows through a transparent screen, but I remarked the same variations. They were indeed even more sensible; for a variation in the distance of the eye of a few centimètres, made a prodigious change in the deepness of the shadows. I observed also that the shadow was much deeper when seen in the line of the light, and that in every other direction, it became paler in proportion as the eye receded from that direction.
[84] Traité de l’éclairage, p. 214.
“In all the cases which I have just described, the differences of the tints when the position is changed, increase in proportion as the shadows are farther separate; and they grow very minute when the shadows are almost touching each other.
Fig. 95.
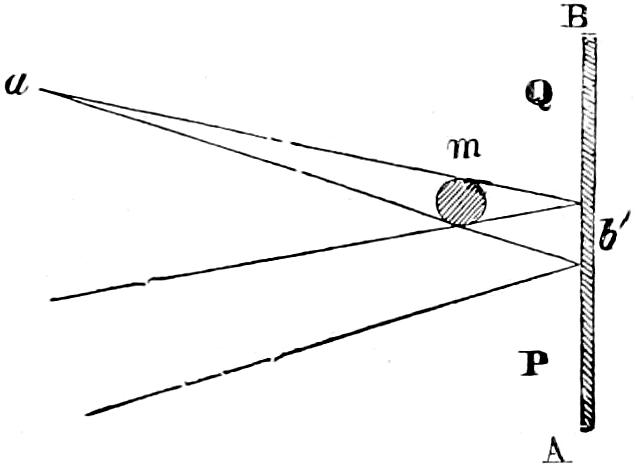
“Let AB (fig. 95) be a white opaque surface, a, a luminous body, and m, a black opaque body, then the shadow b′ cast on AB, will appear deeper when observed from P, than as seen from Q. This is a fact which may be easily verified, and the cause of which is easily conceived. In fact, the surface AB, although it disperses the light, must still reflect more of it, in the directions in which the regular reflection takes place; and hence the rays which are reflected round about the shadow, must have a greater intensity in the direction of P than in that of Q, and, consequently, the shadow b′ must appear deeper from the point P than from Q.
Fig. 96.
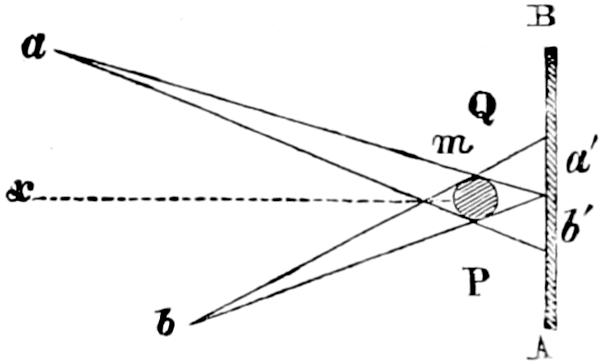
“If we now place (fig. 96) two lights in front of the screen AB, at such distances that the two shadows a′ and b′ should have equal intensities, it is evident that if the eye be placed at P, the shadow b′ must appear[340] more intense than the shadow a′, and that the reverse will take place if the eye be at Q. But the difference which is then observed, arises not only from the difference in the brightness of the parts surrounding the shadows, but also from a difference in the intensity of the shadows themselves; for the shadow b′ is illuminated by b, and radiates much more towards Q than towards P; and, on the contrary, the shadow a′, which is illuminated by a, radiates much more towards P than towards Q. We perceive also why the differences of the tints increase with the separation of the two shadows, and why they become very small when the shadows touch each other; it is because, in proportion as the shadows are farther apart, each of them is illuminated more obliquely, and a greater quantity of light is radiated (by reflection) in the regular direction. When they touch each other, on the contrary, they are illuminated almost perpendicularly, and consequently the shadows radiate light almost equally on either side.
“Those anomalies of a like kind which are observed when the shadows are viewed through a translucent body, such as paper or linen, may be referred to a similar cause. We know, in fact, that, in looking through a translucent medium, we always, more or less, distinctly perceive the luminous body behind it, and, also, that there is a very large proportion of the rays which traverse the body, which stray but a little from the direction which they would follow if the substance were absolutely transparent. Consequently, the space which surrounds the shadow is more luminous in proportion as we come nearer to the direction of the shadow; and as the absolute intensity of the shadows diminishes as we come nearer to the direction of the rays which light them, those two effects concur to increase the intensity of that shadow to which the eye is nearer.
“As the dispersion by reflection is much more complete than by refraction, the variations of which we have just spoken are much greater with a transparent screen, through which the shadows are viewed, than with an opaque screen (from which they are reflected).
[341]
“This, then, is the mode of observing which has appeared to me the best, and by means of which we may obtain very great precision in measuring the intensity of two lights. I view, first, the two shadows in such a manner that both of them may be seen in succession from either side of the body which produces them, and at equal distances. For this purpose I use a good opera-glass. I alter the distance of the flames until in those two positions I perceive the differences (of the intensity in the shadows) to be in opposite directions. The distances of the lamps may then be considered as very nearly in the proper proportion for producing equal shadows, and to make them exactly so, the differences, which are observed on either side (of the centre line between them), should be equal; and, of course, the two shadows themselves, seen at one moment from either side of the opaque body, should be perfectly equal also.[85] These three observations, which mutually serve to verify or correct each other, will lead, with a little practice, to very great precision in the result. We may, also, by using a narrow screen, bring the shadows sufficiently near to touch each other; the variations of the tints then become very small by any change of our position, and we may, in this case, rest content with observing them from one point. To get rid of large penumbrae which are always an obstacle in forming a right estimate of the tints of the shadows, I place the opaque body very near the screen.
[85] I prefer to view the exterior portions of both shadows from the central line itself, in which case the opaque rod stands between them, because, in this manner, I obtain a more correct comparison by the direct contrast of the surfaces than by successive views of them, however quickly taken.
Fig. 97.
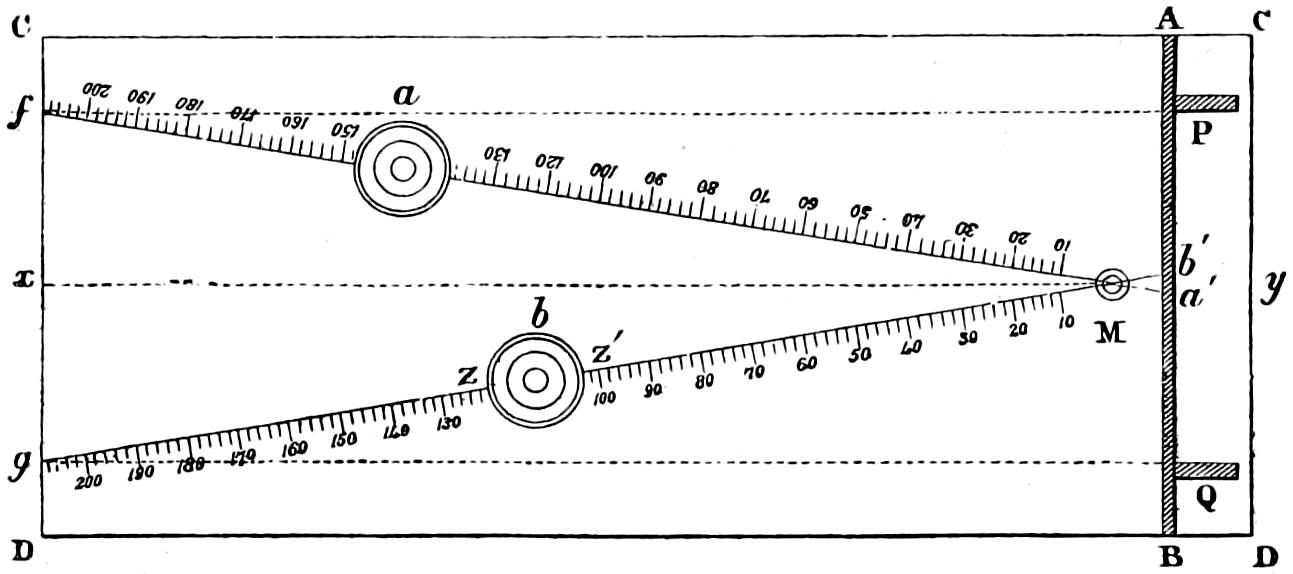
“When we wish to make a great many observations, it is very convenient to mark divisions on the table (which carries the lights), in order to read off, by means of them, the distance of the lamps from the shadows which they illuminate. By this means, each observation need not occupy more than two minutes. I[342] generally use a table CC DD (fig. 97), about two mètres long (6 feet 6 inches), by 80 centimètres wide (2 feet 8 inches). At one end I place the screen AB, covered with white paper, dull (or not glazed), and kept in a vertical plane by two small pieces P and Q. Through the point M, the centre of the opaque body, I draw two lines Mf and Mg, equally inclined to the central line x y, whose extremities b′, a′ are the axes of the two shadows. These lines must be inclined in such a manner that the distance of the shadows may be a little less than the diameter of the opaque body, or so that they may actually touch each other, according to the mode of observing which you wish to follow. These lines M f, M g I divide into decimètres and centimètres, starting from the points a′, b′ and over these lines I place the centres of the flames; the distance between the shadows remains always the same, whatever may be the distance of the lamps: to determine the distance of each lamp from the shadow which it illuminates, we ought, strictly speaking, to take the distance of the centre of the flame b from the point a′; but as the distance from the point b to the point a′ differs little from the distance between the points b and b′, we assume the latter for the former, without causing any sensible error. That distance may be obtained very conveniently by taking the half of the sum of the distances of the two extremities z and z′ of the diameter of the pedestal of the lamp. When the burner is not placed over the centre of the pedestal, we may suspend from it a small plummet,[343] whose point will touch some division and indicate the distance between the centre of the burner and the shadow.
“When the lights are coloured, the shadows are coloured also, and it is then far more difficult to judge accurately of their intensity. They may in that case be much better seen from the point x, as the black opaque body which is interposed between them renders the difference of colour less sensible to the eye.
“The opaque body M is a cylindric rod of iron, whose upper part is blackened in the flame of a lamp, in order to prevent the reflection which might interfere with the sharpness (netteté) of the shadows, and to make them more distinct when they are viewed from the point x.”[86]
[86] Those who feel a curiosity to look farther into this subject may consult Count Rumford’s elaborate paper in the Phil. Trans. for 1794, p. 67.
I shall make a few trifling additions to M. Peclet’s clear description of his excellent mode of measuring the intensity of lights. It is, of course, presumed throughout, that the centres of the flames should be on one level; and I have found it most convenient to place the lamps on small carriages with rollers, which are guided by means of fine strips of wood nailed along the table in the directions gM and fM, and carrying the divided scales of centimètres. This affords the means of making any slight change in the position of the lamps so easily, as entirely to avoid the disturbance of the flame which ensues from lifting the lamp and readjusting it in another position; and will, in practice, be found very convenient when many observations are to be made. I have already said that my own experience has satisfied me that, with the aid of a good opera-glass, the central observation of the two shadows, with the opaque rod between them, is by far the best, and conducts, at once, to a result which is confirmed by the observations of two assistants who watch the shadows at the same time on opposite sides of the table, and at equal distances from them. I have found it convenient in comparing lights, to cover the table with dull black linen cloth, and to surround it with curtains of the same material, hung from slender brackets, in such a manner[344] as to leave space for the observer to move freely round the table within them. The curtains prevent reflection from the walls of the chamber in which the experiments may be conducted, and also lessen the disturbing effects of currents of air. When a comparison of the intensity, and not of the aggregate power of two flames, is to be made, it is necessary to adopt the precaution of inclosing the lights in opaque boxes, with slits of equal area in each, placed on the same level, and so arranged, in reference to the flames, as to be directly opposite the brightest portion of each. After what has been said, it will be almost needless to add that the quotient of the square of the greater observed distance divided by the lesser, is the ratio of the illuminating power of the two flames. The most convenient mode of registering observations, and that which is generally practised, is in the form of a Table like the following:—
| Trials. | Distance. | Squares of Distances. |
Illuminating Power, or Quotient of Squares. |
|||
|---|---|---|---|---|---|---|
| Lamp A. | Lamp B. | Lamp A. | Lamp B. | Lamp A. | Lamp B. | |
| 1 | 143 | 140 | 20,449 | 19,700 | 1·00 | 0·958 |
| 2 | 117 | 114 | 13,689 | 12,996 | 1·00 | 0·949 |
As a standard lamp by which to test others, I believe few will be found superior to the best Carcel lamp, which has a clockwork movement, and whose flame continues to increase in power for about four hours after it is lighted; after which it maintains its state permanently, until the supply of oil fails. This fact was verified by M. Peclet with the greatest care. “I took,” says he, “two similar lamps. They were lighted at the same time, and their relative intensities were measured. One was then extinguished, without touching the wick, and its clockwork movement was stopped. One hour afterwards, I set the clockwork in motion and relighted the lamp, but without touching the wick. It was found in the same state as at the first comparison, and I measured its intensity in reference to the first. Those experiments[345] I repeated every hour, and these are the results which I obtained. The lamp which I call No. 1, is that which remained continually burning; No. 2, is that which was only lighted during the continuance of the (successive) observations.”
| Times of Observation. |
Intensities. | ||
|---|---|---|---|
| Lamp, No. 1. |
Lamp, No. 2. |
||
| H. | M. | ||
| 5 | 30 | 100 | 100 |
| 6 | 30 | 103 | 100 |
| 7 | 30 | 106 | 100 |
| 8 | 30 | 110 | 100 |
| 9 | 30 | 117 | 100 |
| 10 | 30 | 117 | 100 |
| 11 | 30 | 117 | 100 |
| 12 | 30 | 117 | 100 |
This curious scale of increase in power, seems to be solely due to a peculiarity of the manner in which the lamp, that derives its supply of oil by clockwork, becomes heated; and the effect may be described as follows: The heating of the wicks, the chimney, and the oil in this burner, as in that of all other lamps, tends to increase the light; but, in an ordinary lamp, acting by a constant pressure, this maximum of heat is soon attained; whereas in the clockwork-lamp, into the burner of which the oil is thrown up by a pump, the whole of the oil in the cistern must reach its maximum temperature before the best effect of that lamp is produced. After this state has been reached, there is no disturbing influence at work, and the lamp burns steadily as long as the oil lasts.
I have myself tried what may naturally appear to be the most simple mode of obtaining an unvarying standard-light, by employing a gas-burner, supplied from a gasometer under a constant pressure; but I found it very difficult to obtain satisfactory proof of the constancy of the pressure; and in a large town, where there are many burners around one, their lighting or extinction is found to[346] exercise a material influence in changing the condition of the flame. I must confess that I have always been disappointed in attempting to use a gas-flame as a standard of comparison.
There are various dangers on the shores of Britain, more especially at the entrance of the great estuaries of England and also in Ireland, whose position is such as to put them beyond the reach of regular lighthouses. Sand-banks which are too soft to sustain a solid structure, and have too deep water on them to admit of the erection of screw-pile lighthouses, are often the sites for Floating Lights. mooring light-vessels, to guide the mariner into the entrance of some estuary, or enable him to thread his way through the mazes of gats and channels, which, even during the daytime, baffle the mariner, who sees no natural object on the low sandy shores of the neighbouring coast to help him to guess at his true position. The first Light-vessel moored on the coast of Great Britain, was that at the Nore in 1734. There are now no fewer than 26 floating lights on the coast of England.
By the kindness of the Elder Brethren of the Corporation of Trinity House of Deptford Strond, I am enabled to give the following brief sketch of the nature and peculiarities of Floating Lights which was communicated to me by Mr Herbert, the secretary of the Corporation:—
“The annual expense of maintaining a Floating Light, including the wages and victualling of the crew, who are eleven in number, is, on an average, L.1000; and the first cost of such a vessel, fitted complete with lantern and lighting apparatus, anchors, cables, &c., is nearly L.5000. The lanterns are octagonal in form, 5 feet 6 inches in diameter; and, where fixed lights are exhibited, they are fitted with eight Argand lamps, each in the focus of a parabolic reflector of twelve inches diameter; but, in the revolving lights, four lamps and reflectors only are fitted. The greatest depth of water in which any light-vessel belonging to the Corporation of Trinity House of Deptford Strond at present rides, is about 40 fathoms (which is at the station of the Seven Stones between the Scilly Islands and the coast of Cornwall).
[347]
“The Corporation’s light-vessels are moored with chain-cables of 1¹⁄₂ inch diameter, and a single mushroom anchor of 32 cwt., in which cases the chain-cables are 200 fathoms in length; some of the said vessels are moored to span-ground moorings, consisting of 100 fathoms of chain to each arm, and a mushroom anchor of similar weight at the end of each; a riding cable of 150 fathoms being in such cases attached to the centre ring of the ground chain. The tonnage and general dimensions of the light-vessel are given on the drawing of the lines.” (See Plate XXIX.)
Still lower in the scale of “signs and marks of the sea,” are Beacons and Buoys. Beacons and Buoys, which are used to point out those dangers which, either owing to the difficulty and expense that would attend the placing of more efficient marks to serve by night as well as by day, are necessarily left without lights, or which, from the peculiarity of their position, in passages too intricate for navigation by night, are, in practice, considered to be sufficiently indicated by day-marks alone. Beacons, as being more permanent, are preferred to Buoys; but they are generally placed only on rocks or banks which are dry at some period of the tide. On rocks, in exposed situations, the kind of Beacon used is generally that of squared masonry, secured by numerous joggles (as shewn at Plate XXXII.); and in situations difficult of access, and in which works of uncompleted masonry could not be safely left during the winter season, an open framework of cast-iron pipes, firmly trussed and braced, and secured to the rock with strong louis-bats, is preferred. The details of this framework are shewn at Plates XXX. and XXXI. A stone Beacon of the form and dimensions shewn in Plate XXXII., may be erected for about L.700, and the iron Beacon shewn at Plate XXX., for about L.640. In less exposed places, where the bottom is gravel or hard sand, a conical form of Beacon, composed of cast-iron plates, united with flanges and screws, with rust-joints between them, is sometimes used. A Beacon of this kind is shewn at Plate XXXII., which can be erected for about L.400.
Lastly, Buoys, which may be regarded as the least efficient[348] kind of mark, and as bearing the same relation to a Beacon that a Floating-light does to a Lighthouse, are used to mark by day dangers which are always covered even at low water, and also to line out the fair-ways of channels. They are, for the most part, of one of the three forms shewn in Plate XXXIII., viz., the Nun-buoy, in the form of a parabolic spindle, generally truncated at one end, so as to carry a mast or frame of cage-work, and loaded at the other end, so as to float in a vertical position; the Can-buoy, which is a conoid floating on its side; and, lastly, the Cask-buoy, which is a short frustum of a spindle truncated at both ends, but almost exclusively used for carrying the warps of vessels riding at moorings. Those buoys are of various sizes and differ in cost. Mast-buoys, from 10 to 15 feet in length, cost from L.23, 15s. to L.48; and those of the Ribble and the Tay, which are 21 and 24 feet long, cost respectively L.105 and L.79; the Can-buoys are from 5 to 8 feet long, and cost from L.13, 13s. to L.20, 5s. Large buoys are often built on kneed frames resembling the timbers of vessels. The Cask-buoy is generally 6 feet long, and costs L.22, 15s. All these buoys are formed of strong oaken barrel-staves, well hooped with iron rings, and shielded with soft timber; and the nozzle-pieces at the small end of the Nun and Can buoys are generally solid quoins of oak, formed with a raglet or groove to receive the ends of the staves. Much skill, on the part of the cooper, is required in heating and moulding the staves to the required form; and great care must be taken that they be of well-seasoned timber. Buoys are not caulked with oakum, but with dry flags closely compressed between the edges of the staves, which swell on being wet; and they are carefully proved by steaming them like barrels, to see if they be quite tight. Buoys are also formed of sheet-iron, in which case they are sometimes protected with fenders of timber; but they have been found more troublesome for transport, and, for most situations, are considered less convenient than those of timber.
In the beginning of 1845, I suggested the idea of rendering Beacons and Buoys useful during night, by coating them with some[349] phosphorescent substance, or surmounting them with a globe of strong glass filled with such a preparation, whose combustion is very slow, and emits a dull whitish light and little heat. Some experiments were accordingly made by my suggestion; but I cannot add that any practically useful result has been obtained.
In laying down Beacons or Buoys, their position is fixed, as may be seen in the Table in the Appendix, either by the intersection of two lines drawn through two leading objects on the shore (the magnetic bearings of which are given for the sake of easy reference on the spot, in finding out the marks), or by means of the angles contained between lines drawn to various objects on the shore, which meet at the Beacon or Buoy from which they are measured by means of a sextant. In the latter case, the angles are always measured around the whole horizon, thus affording a check by the difference of their sum from 360°. The magnetic bearing of one of those lines is afterwards carefully ascertained, by means of the prismatic compass (if possible from one of the objects on shore, and if not, conversely from the Beacon or Buoy), so as to afford the means of translating the whole into magnetic bearings for the use of seamen. The buoys are moored, as shewn in Plate XXXIII., by means of chains and iron sinkers, with a sufficient allowance in the length of the chain to permit them to ride easily.
The column is generated by the revolution of a rectangular hyperbola about one of its asymptotes. In the annexed figure (No. 98), a f is the height of the column, a c and f h the radii of its base and top; and we have to determine the particular hyperbola which will pass through the points c, h.
Putting b e = x; e g = y, the equation to the curve, referred to its asymptotes, is
x y = a²2,
in which the value of the constant a² 2 is to be found. For this purpose we have the conditions a c = 21; f h = 8; and a f = 120·25. Let the co-ordinates of the point c be x′, y′, and of h, x″, y″, then y′ = 21; y″ = 8; x″ = x′ + 120·25.
Fig. 98.
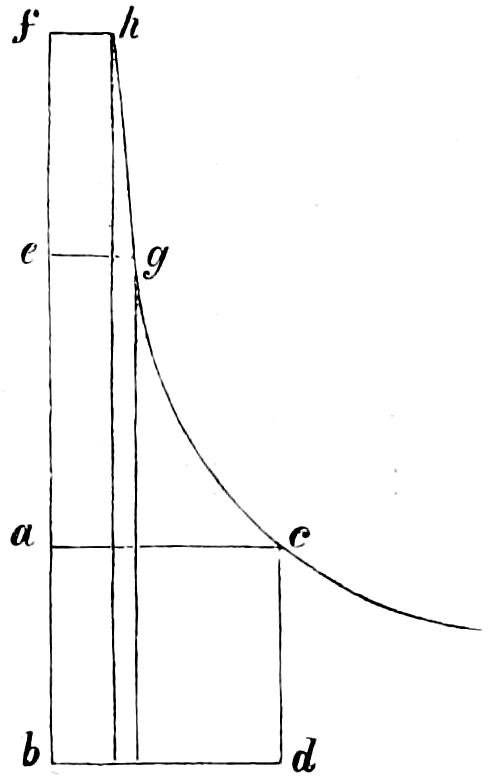
| And since | x′ y′ = a²2 = x″ y″ |
| we have | 21 x′ = 8 (x′ + 120·25) |
| from which | x′ = 74 |
| and | a²2 = x′ y′ = 74 × 21 = 1554. |
| Therefore | x y = 1554. |
Transferring the origin to a, x becomes x - x′ = x - 74, and y (x - 74) = 1554, and the required equation by which the following Table was computed is, y = 1554 x - 74.
[354]
Table of the Radii of the Hyperbolic Column at each foot of its Height.
| Height. | Radius. | Height. | Radius. | Height. | Radius. | Height. | Radius. |
|---|---|---|---|---|---|---|---|
| 0 | 21·000 | 31 | 14·800 | 62 | 11·426 | 93 | 9·305 |
| 1 | 20·720 | 32 | 14·660 | 63 | 11·343 | 94 | 9·250 |
| 2 | 20·447 | 33 | 14·523 | 64 | 11·261 | 95 | 9·195 |
| 3 | 20·182 | 34 | 14·389 | 65 | 11·180 | 96 | 9·141 |
| 4 | 19·923 | 35 | 14·257 | 66 | 11·100 | 97 | 9·088 |
| 5 | 19·671 | 36 | 14·127 | 67 | 11·021 | 98 | 9·035 |
| 6 | 19·425 | 37 | 14·000 | 68 | 10·944 | 99 | 8·983 |
| 7 | 19·185 | 38 | 13·875 | 69 | 10·867 | 100 | 8·931 |
| 8 | 18·951 | 39 | 13·752 | 70 | 10·792 | 101 | 8·880 |
| 9 | 18·723 | 40 | 13·632 | 71 | 10·717 | 102 | 8·830 |
| 10 | 18·500 | 41 | 13·513 | 72 | 10·644 | 103 | 8·780 |
| 11 | 18·282 | 42 | 13·397 | 73 | 10·571 | 104 | 8·730 |
| 12 | 18·070 | 43 | 13·282 | 74 | 10·500 | 105 | 8·681 |
| 13 | 17·862 | 44 | 13·170 | 75 | 10·430 | 106 | 8·633 |
| 14 | 17·659 | 45 | 13·059 | 76 | 10·360 | 107 | 8·586 |
| 15 | 17·461 | 46 | 12·950 | 77 | 10·291 | 108 | 8·539 |
| 16 | 17·267 | 47 | 12·843 | 78 | 10·224 | 109 | 8·492 |
| 17 | 17·077 | 48 | 12·738 | 79 | 10·157 | 110 | 8·446 |
| 18 | 16·891 | 49 | 12·634 | 80 | 10·091 | 111 | 8·400 |
| 19 | 16·710 | 50 | 12·532 | 81 | 10·026 | 112 | 8·355 |
| 20 | 16·532 | 51 | 12·432 | 82 | 9·962 | 113 | 8·310 |
| 21 | 16·358 | 52 | 12·333 | 83 | 9·898 | 114 | 8·266 |
| 22 | 16·188 | 53 | 12·236 | 84 | 9·835 | 115 | 8·222 |
| 23 | 16·021 | 54 | 12·141 | 85 | 9·774 | 116 | 8·179 |
| 24 | 15·857 | 55 | 12·046 | 86 | 9·712 | 117 | 8·136 |
| 25 | 15·697 | 56 | 11·954 | 87 | 9·652 | 118 | 8·094 |
| 26 | 15·540 | 57 | 11·862 | 88 | 9·593 | 119 | 8·052 |
| 27 | 15·386 | 58 | 11·773 | 89 | 9·534 | 120 | 8·010 |
| 28 | 15·235 | 59 | 11·684 | 90 | 9·476 | 120·25 | 8·000 |
| 29 | 15·087 | 60 | 11·597 | 91 | 9·418 | ... | ... |
| 30 | 14·942 | 61 | 11·511 | 92 | 9·361 | ... | ... |
[355]
Fig. 99.
The reflector-plate consists of virgin-silver and the purest copper (from the ingot), in the proportion of 6 oz. of silver to 16 oz. of copper. The two metals are in pieces, forming a flat parallelopepid of about nine inches of surface. Being first thoroughly scraped and cleared from rust with a file, they are tied together with wire and placed in the furnace, where they are united by means of a flux composed of burnt borax and nitre, mixed to the consistence of cream. Their thickness is sufficient to admit of their being repeatedly passed through the rolling-mill, so as at last to come out a plate twenty-eight inches square. Every time it is passed through the rollers, the plate is annealed in the furnace before being again pressed. It is then cut into a circular disc ready for working; and great care should be taken to keep the metal perfectly clean during the whole of the hammering and polishing processes. The first step towards forming the plate to the curve, is to raise the back or copper side to a slight convexity by beating, with the boxwood mallet (fig. 99), rounded at each end, c and d, its inner or silver side upon a large block of beechwood, of a form slightly concave. This beating is begun at the edge of the plate, and gradually reaches the centre. After the disc has been raised to the proper height on the wooden block,[356] the next step is to take it to the horse (fig. 103, opposite page), where it is beaten with the wooden mallet (fig. 100), its concave face being in contact with the bright steel-head a (fig. 103), until it has nearly reached the proper height for the reflector, for which the workman has a gauge or mould to guide him; in this course of raising, as it is called, the peened face b a b (fig. 100) is first used, and then recourse is had to the opposite or flat face for smoothing it after being raised. In this last course of raising, as well as in the process of smoothing the reflector all over, the workman bestrides the horse.
Fig. 100.
Fig. 101.
During the process of raising with the peened side of the mallet, an external mould FGHF (fig. 101), with a needle-point P, at its vertex, is applied, to indicate its proper position with reference to the mould; and allowance is made on the height and diameter of the reflector to meet the expansion of the metal during the hard-hammering which is to follow. After each course of the raising with the wooden mallets, the reflector must be annealed in the following manner:—The reflector is first damped with clean water, and its surface dusted over with a powder, composed of one pint of powdered charcoal to one ounce of saltpetre, which is applied by means of a thin flannel bag. The reflector is then put on a clear charcoal fire, where it is turned round as the powder flies off, which is an indication that the metal is duly heated. Over-heating is very injurious. When removed from the fire, the reflector is plunged into a large tub, containing what is called the pickle, which is a solution of one quart of vitriol in five or six gallons of water. After this it is washed with clean water, and scoured with Calais sand.
The next step is to put the reflector, thus raised nearly to its true form, into an iron stool, where a small hole being drilled in its vertex, a circle is described from this point with a beam-compass, so as to cut the paraboloïd to the proposed size.
[357]
Fig. 102.
Fig. 103.
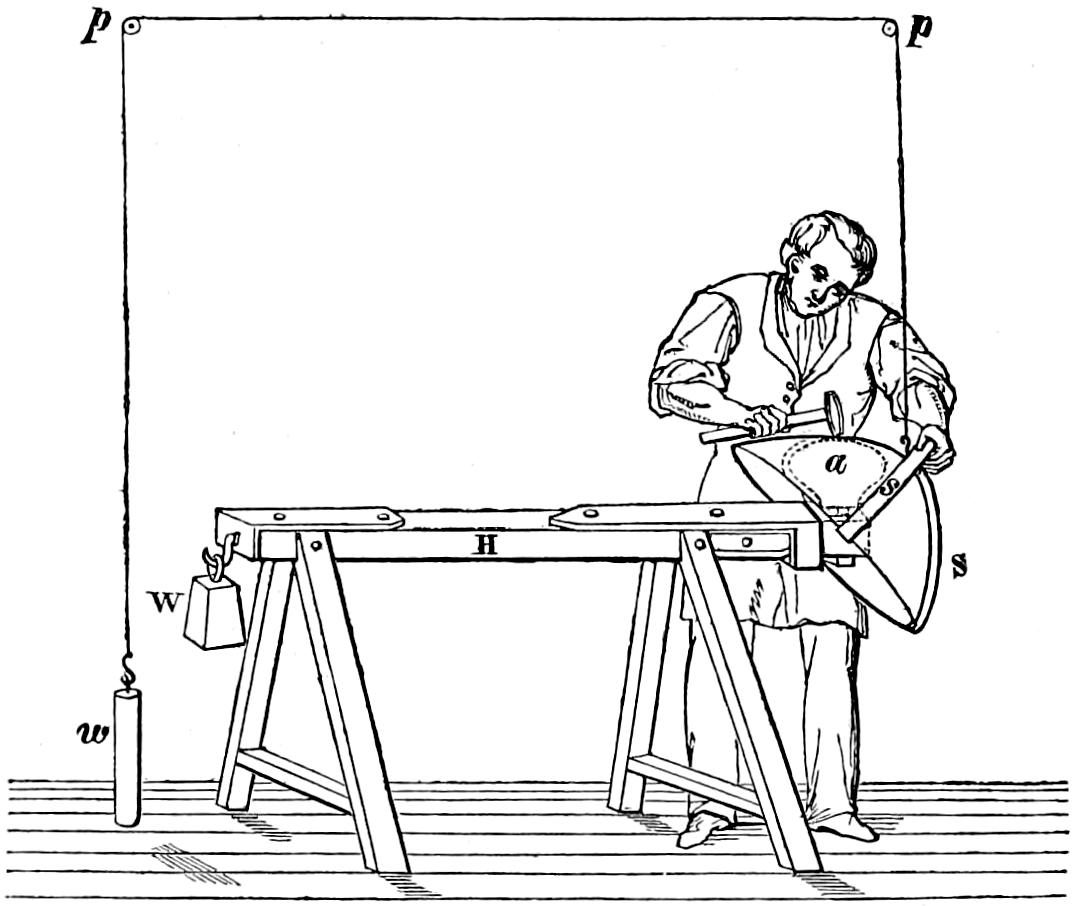
Fig. 104.

Fig. 105.
The reflector is next hard-hammered all over (or planished, as it is technically termed) on the bright steel-head a (fig. 103), with the planishing hammer (fig. 102); and to facilitate working, the reflector is slung in a flexible frame SS, and counterbalanced by a weight w, hanging by a cord over the pulleys p p. When the reflector is all planished over, the next process is the smoothing, which is done on the steel-head a, with a lighter hammer (fig. 104 ), muffled with fine parchment at each end. After it is smoothed comes the finishing, or what is called the filling up to the mould. This is a tedious process, and the workman requires continually to have recourse to the marble table at M, on which he lays the reflector, as shewn in fig. 105, and applies to successive portions of its surface the mould g n, which has a needle-point centred at n, in the small hole drilled in the vertex. During this examination, he marks with a fine slate-pencil those portions of the reflector which do not meet the mould g n. The parts, so marked, are gently gone over with the muffled hammer, until every point touches the mould. This last process requires great caution; for, if any part of the surface be raised above the gauge, it is hardly possible to remedy it. Such a mistake, indeed, can only be corrected by annealing the reflector afresh,[358] and bringing it back to the true form with the mallet; but reflectors so cobbled are never good. The table M (fig. 105) rests on a square box C, in which the tools and moulds are kept.
Fig. 106.
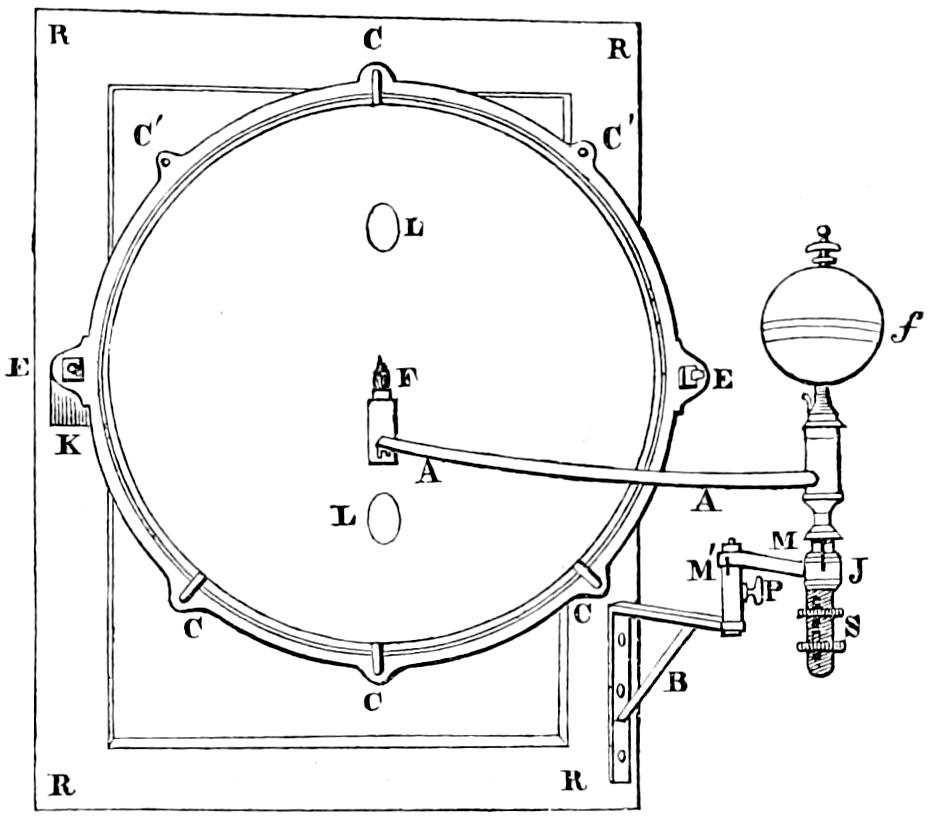
When thus finished from the hammer, the reflector is put into the apparatus shewn in fig. 106, which is placed at the end of a long dark corridor. RR is a wooden frame fixed to the wall with projecting brackets at K, which carry the reflector, fixed at E, E, by means of screws, so as always to have a definite position with reference to the bracket B, which carries the lamp and its fountain f, so arranged that its flame may admit of perfect adjustment to the point which ought to be the focus of the reflector. For the purpose of this adjustment, S shews screws for raising and depressing the level of the burner; and the lines or marks M, M′ shewn at the sockets J being brought into line, regulate the position of the burner in the plane of the focus, after it has been raised to the level of that plane by means of the screws at S. The lamp being lighted and thus properly placed, its effect on the reflector’s surface is observed by some one stationed at a convenient distance; and if the whole surface appear luminous, the instrument is considered fit for polishing; but if any dark spaces be found in it, the whole reflector must be again carefully tested by means of the mould, and the defective parts remedied in the manner above described.
The next step is to turn over the edge of the reflector, so as to stiffen it. For this purpose it is placed in the matrix P′P′ (fig. 107), and the needle-point at V is adjusted by the screw at D, so as just to enter the small hole formerly drilled in the vertex of the reflector. The die-plate PP (which is worked by means of the arms AA, which turn the screw S) then descends and presses the edge over, which is finished with a finely polished tool C, revolving round the axis of the instrument, which coincides with the centre of the matrix and die. In order to ensure a steady vertical movement of the die-plate PP, cross-arms FF, which are provided with sockets HH,[359] which slide over the rods GG, GG, are added to prevent any lateral shake or derangement. The whole frame is stiffened by the cross-head in which the screw S works.
Fig. 107.
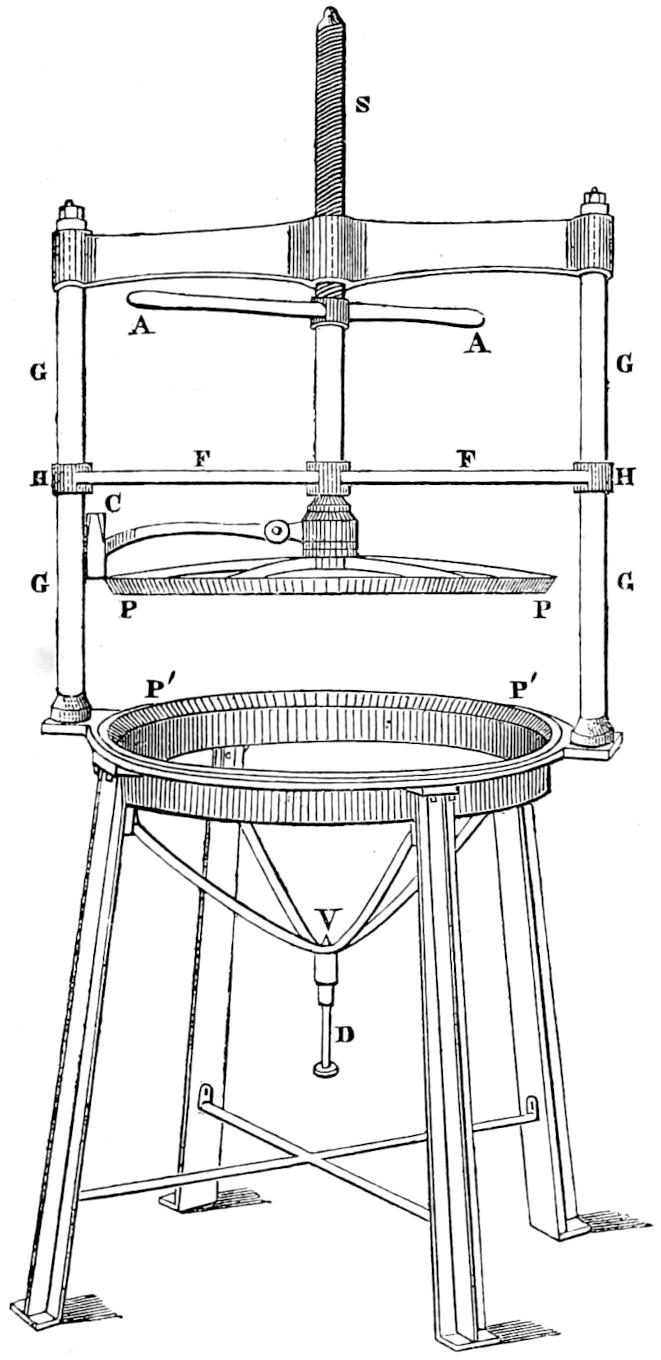
Fig. 108.
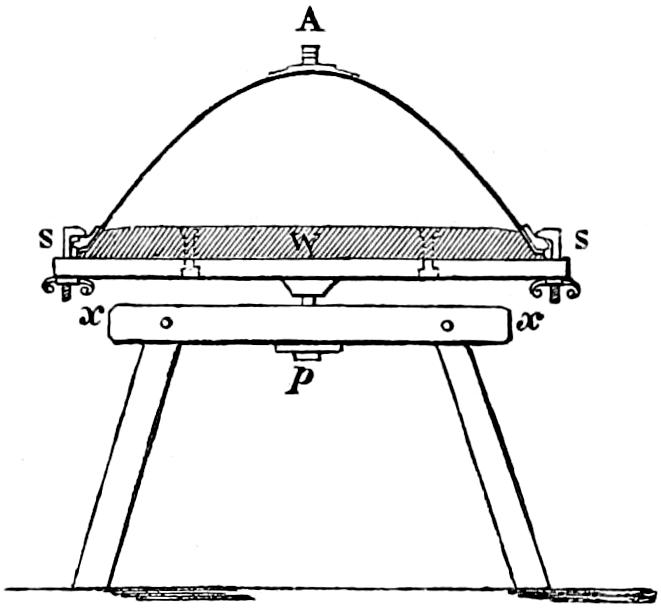
Fig. 109.
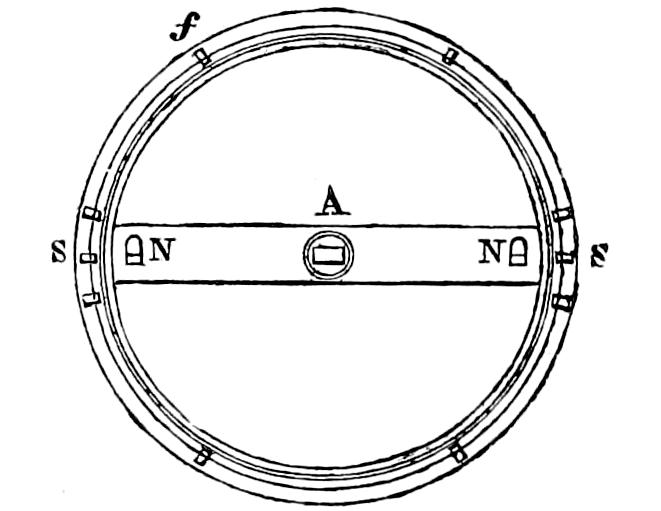
The reflector is then placed on the circular cast-iron table (figs. 108, 109), to which it is attached by the clamp-screws S, S. In this position, the bizzle W (fig. 108) and back-belt NAN (fig. 109), are soldered on. After this the reflector is ready for being finally polished; for which purpose, it is placed in a chaise percée, padded round the edges, and is first scoured all over with a piece of pure charcoal of hard wood, and next with a mixture of Florence oil and finely washed rottenstone, applied by means of a large ball of superfine cloth. It is then carefully cleansed with a piece of fine flannel dipped in Florence oil, and afterwards dusted over with the[360] powder of well washed whiting, and wiped out with a soft cotton cloth. Lastly, it is carefully rubbed by the naked hand, with finely washed rouge and clean water, and wiped with a smooth chamois skin. In all the polishing and cleansing processes, some skill in manipulation is required, as the hand is generally moved in such a manner as to describe successive circles with their planes parallel to the lips of the reflector, and their centres in the axis of the generating curve.
The prices paid to the workmen for the various departments of the reflector-making are generally as follows:—
| Raising the plate to the curve, with the wooden mallet, | L.0 | 10 | 0 |
| Hammering and smoothing to the mould, | 1 | 5 | 0 |
| Finishing in the die, and putting on bizzle and back-belt, | 0 | 6 | 0 |
| Polishing, | 0 | 12 | 0 |
| L.2 | 13 | 0 |
The prices paid to the manufacturer were for the large reflectors of 24 inches aperture, L.43; for the small ones of 21 inches, L.31, 12s. The lamp with the sliding-carriage, required for each, costs L.6.
[361]
The glass used in all the parts of the optical apparatus of the dioptric Lighthouses is that of St Gobain, whose index of refraction is 1·51.
As well on account of the difficulty experienced in producing at all times regular castings of glass from the moulds, as in order to compensate for the frequent accidents, which occur in the first application of the rubbers to the inequalities of the surface of the glass, the castings, whether for rings of lenses or prisms, are made from moulds, exceeding the intended size of the finished pieces by one-eighth part.
We shall take as an example, which is well calculated to illustrate the difficulties of the grinding process, one of the prismatic rings of a Catadioptric Light of the first order. The first operation will be to take off the rough arris at the angles of the pieces as they come from the moulds, and to reduce to equality the length of each of the four quadrantal prisms or segments by removing from each the quantity that may be necessary to make those four pieces, when placed on a circle, exactly equal to that of the finished zones. Each of them must have an excess of material at the various surfaces just sufficient to insure the rubber having scope enough to remove all the flaws or defects of the two surfaces to be first ground, which are the (concave and convex) refracting faces of the zone (the sides AC and BC in the Table in the Appendix, No. IV.)
Fig. 110.
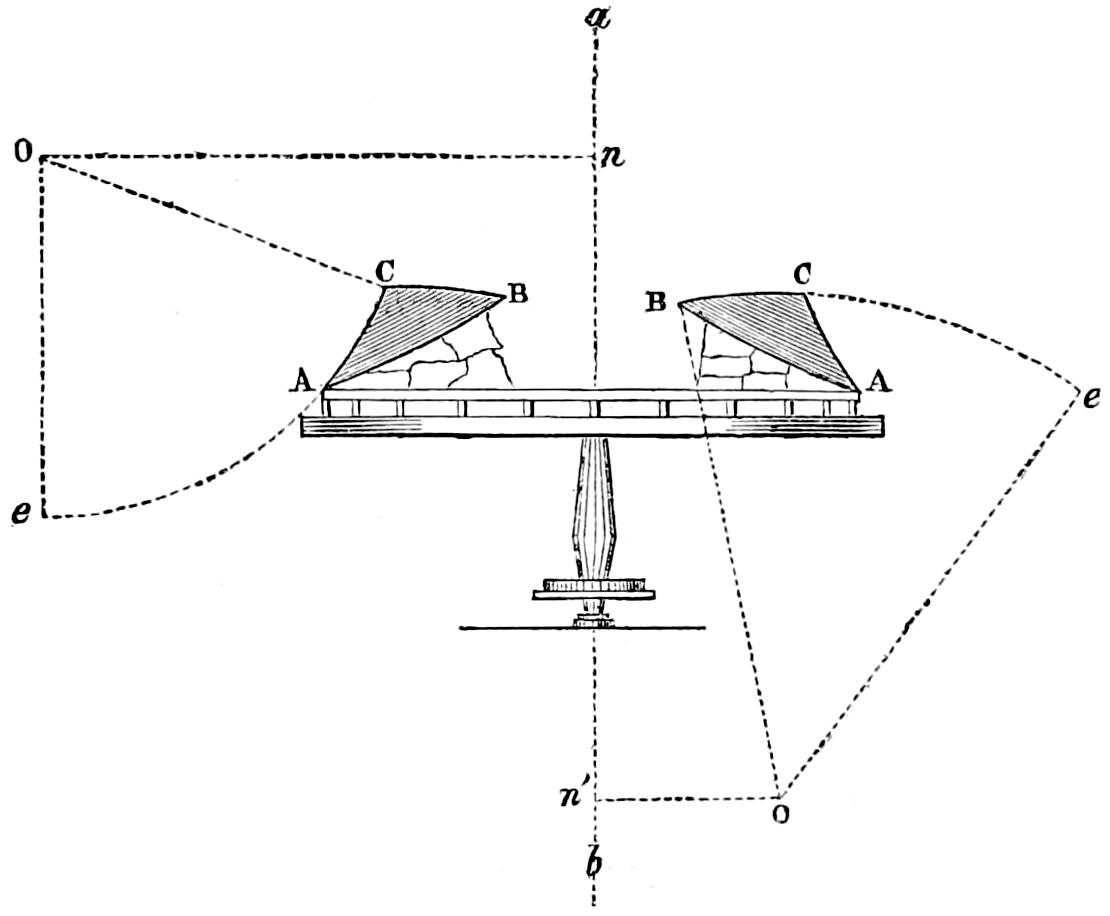
The pieces must be placed end to end on the horizontal plane or table of the lathe at AA (fig. 110), and must rest on the exterior arris A of the reflecting side, on which arris[362] there is ground a narrow plane whose width is proportionate to the projection of the outer edge beyond the inner edge of the zone, foreshortened by the bevel or inclination of the reflecting side, when resting (as in fig. 110) on the circular iron belt, which is screwed to the table of the lathe provided for its reception. This narrow plane at the arris A should be sufficient to give the prism a solid and regular bearing on the circular iron belt. In this figure (fig. 110) a b is the vertical axis of the lathe, n the point from which the co-ordinates for O, the grinding centre for the exterior concave refracting surface AC, are measured, and e AC the arc swept by the grinding surface. Conversely, n′ is the origin of the co-ordinates for the grinding centre O of the interior convex refracting surface BC, and e CB the arc swept by its grinding surface. Some skill is required in fixing the prism on the belt, for, on the one hand, there is an obstacle to correct workmanship from the dragging motion of the platform, and, on the other, by the unequal subdivision of the weight of the glass, which should be nearly balanced. This narrow plane being perfectly adjusted for all the segments so as to bed them quite level, the circular iron belt on which the ring should be ground, is placed on its platform, in the manner represented in the figure. It should be as truly levelled as possible, otherwise all the subsequent operations will be deranged by it. This iron belt is heated by means of heating pans; and the degree of heat may be practically judged of by the ebullition of drops of water let fall on it. The segments of glass are also at the same time placed in a stove heated with steam, and are generally raised to about 120° centigrade. The difference between the time required for the two operations of heating the iron belt and the glass segments is employed in laying or bedding a quantity of cement on the reflecting side of the segment, so as to fill up the angular space between the glass and the iron belt, and also to serve as a seat for the segment in the manner shewn in fig. 110. This operation is performed on a plane surface, in order that the lower part of the mastic may be precisely on a level with the narrow plane already ground on the outer arris of the reflecting side. After being sure that the heat is equally spread over every part of the circular iron belt, the segment is arranged on it; and the workman must, at this juncture, exert all his skill in placing the parts of the segment in a position nearly concentric with the belt, or in a truly circular form, making due allowance, however, for the inequalities existing at various parts of the rough material, and at the same time taking care that there should be an interval of at least two millimètres (or about ¹⁄₁₂th inch) between the ends of each of the two adjacent segments. Without this interval the heat evolved during the polishing would either dilate the glass so[363] much as to cause the ends of the segments to fly into splinters, or make it needful to remove the zone before this should take place, the inevitable consequence of which would be the fracture of the pieces. Those intervals between the segments are filled with statuary’s plaster, which must be carefully washed and brushed at each change of the emery employed in grinding.
The exterior diameter of the circular iron belt must be precisely equal to that of the ring, because, if larger, the free movement of the rubbers to and fro on the concave refracting surface AC (fig. 110) could not take place.
By what is already said, it will be obvious that the grinding process is begun at the refracting sides AC and BC, and a few words will shew that this could hardly be otherwise. If a commencement be made on the reflecting side, which appears at first sight more natural, the consequence is obvious. Having provided for an excess of material in every direction, the segment must consequently be larger than it will be when finished; and the surfaces therefore cannot be true and perfect, except they be ground throughout their entire segmental section, from their centres of curvature, in reference to some given apex of the generating triangle. Now, if the reflecting side were finished first, it might continue to possess this excess of size after being finished, and would, therefore, afford no accurate starting point for the grinding of the other surfaces; it would also present no surface or narrow plane for resting firmly on the iron belt, but would then depend merely on its own finished plane, which, being curved and considerably inclined, would not give a solid bearing for the glass. The other mode of commencing with the two refracting sides, on the contrary, gives a solid bearing on the narrow plane already ground on the reflecting side at A; and after these surfaces have been ground, and the segments inverted (as shewn in fig. 111), the outer edge of this narrow plane at the arris A, which has been fully defined by the intersection of the finished surface AC just ground, and also the apex at C, which has been determined by the intersection of AC and BC, combine to fix an accurate starting point for the rubber, in grinding the reflecting surface AB.
Fig. 111.
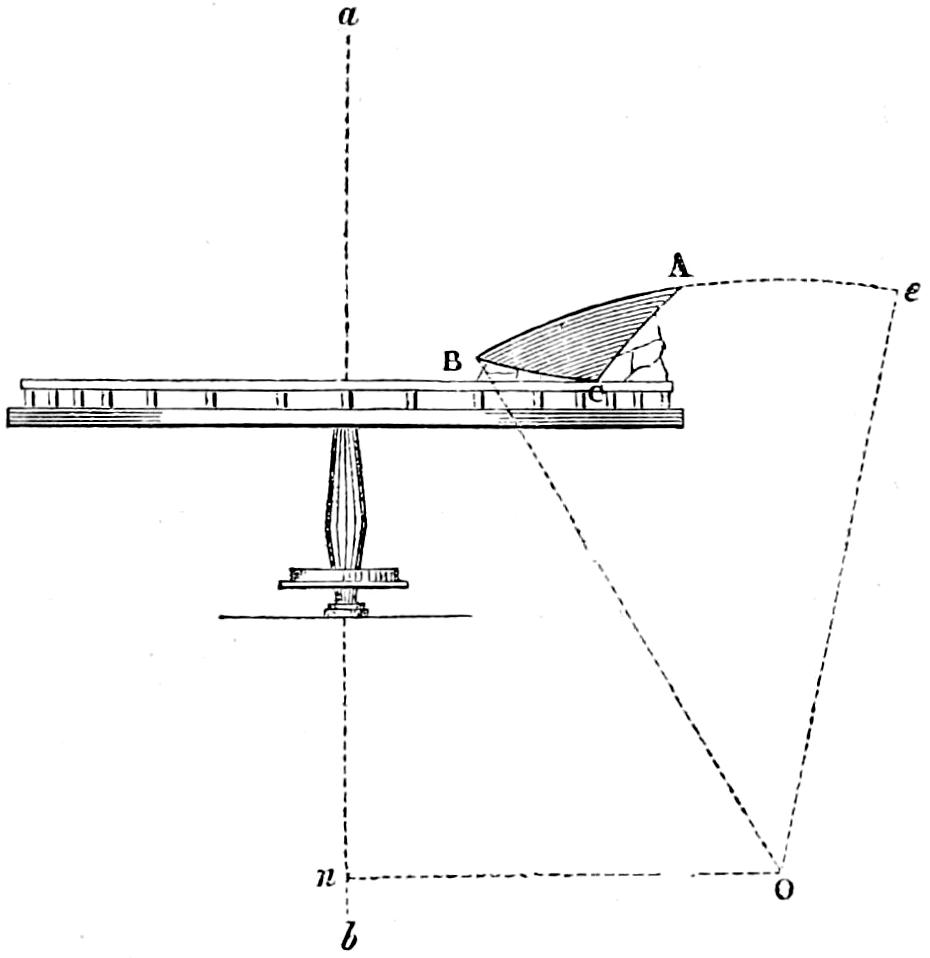
[364]
The ring is generally reduced from the rough state by means of fixed rubbers, the adjustment of which is more easily regulated than that of the moveable beam or radius of the arc, which is used to give the exact curvature of the surface. Those fixed rubbers are 150 millimètres (nearly 6 inches) wide, by 200 millimètres (nearly 8 inches) long, and are of cast-iron. Three such rubbers are placed at equidistant points of the circle. Two cutters of sheet-iron attached to arms placed vertically (as are also those which carry the rubbers), and moving in grooves radiating towards the centre of the lathe, so as to admit of adjustment to suit the varying radii of the zones, serve gradually to abrade the outer and inner arrises of the segments, so as to prevent the splintering to which, from becoming too sharp, those arrises, without this precaution, would be liable. Those rubbers are, besides, fixed by stems to frames, in the form of quadrants of the circle, which allow of a change in the direction of the planes, as occasion may require.
Instead of the siliceous sand formerly used, the powder of pounded freestone is employed, as it is found to wear the tools less, and to form a better preparation for the subsequent grinding operations. It is easy to conceive that the action of the fixed rubbers necessarily produces ruts or inequalities in the circular direction. The operation of rough dressing, therefore, is not finished until, when those first rubbers are removed, the surfaces of the segments have been subject, for the required time, to the action of moveable rubbers, attached to arms working as radii of curvature, in a plane at right angles to the horizontal movement of the lathe, which carries the zones.
The form of the segment should be nearly perfect, after the rough grinding is finished. The lathe and the zone are then subjected to an extremely careful washing. Every place where the stone-powder might adhere is dusted. The radius of curvature is verified afresh, agreeably to the co-ordinates (Appendix, No. IV.); and emery is used instead of powdered stone; beginning with that called No. 1, which is drawn after suspension in water for one minute. Brushes are used for spreading the emery on the surface of the glass. The quantity ought always to be sufficient to prevent the direct contact of the cast-iron rubber with the glass. Splintering or scratching,[365] which cannot be easily effaced, may result from the neglect of this precaution.
Practice alone, and an eye duly trained by continual experience, can determine the point of time at which each kind of emery must be discontinued. The celerity of the work depends on circumstances very difficult to appreciate, such as the amount of the pressure of the rubbers, or the degree of accuracy with which the radius of curvature has been adjusted, during the rough grinding. Each kind of emery in succession thus corrects the form of the zone and refines the grain of the surface of the glass; and each change to a fresh material requires the same attention to cleanliness, so as to remove every trace of the substance last used in grinding, and thus to give each successive process its full and legitimate effect. The douci is the fifth and last kind of emery which precedes the polish. It is drawn off after ten minutes’ suspension in water, and is extremely fine. Before applying it, the greatest care is necessary to insure cleanliness, as a single grain of any of the preceding kinds of emery might cause scratches, which the polish cannot remove.
The same considerations which induce the workman most carefully to cleanse the lathe and everything connected with it, before employing the last emery called the douci, are still more urgent in the case of the final polish. The only change which is made at this last stage of the work is to replace the first rubber by a new one, both longer and wider by about 50 millimètres (nearly 2 inches). On its lower face is attached with cement a piece of soft carpet, whose edges are fixed to the rubber by means of flat bands of iron, attached with screws. This security, added to that given by the cement, is necessary to fit it to resist the great pressure it must sustain. A practical question, which experience alone can resolve, occurs at this stage, as the operation of polishing may, in the hands of unskilful persons, be so inopportunely commenced, as to make that work almost endless. Thus, the mere circumstance of spreading at the beginning too thick layers of rouge, or using unsuitable kinds of carpet, would cut scratches in the glass, and thus perhaps make it necessary to return to the use of the emery called douci. Sometimes, also, if the carpets be not washed at the very time of using them, scratches are formed by the dust which they may contain. This shews, that the use of rouge should be rather sparing than otherwise, at the commencement of the polish; and that the carpet-cloths should be brushed and washed[366] twice rather than once. In all cases, the quality of the carpet forms an important element in the success of the working.
When the polish is finished, the ring is detached from the circular belt, simply by the tap of a hammer, on the inner edge of the circle. The division of the zones (which are quarters of the circle) into eighths, is done by means of a sawing machine consisting of a flat copper-wheel, one-half millimètre (¹⁄₅₀th inch) in thickness, attached to an arm with a counterpoise. This wheel descends and cuts the zone by means of emery, which is continually applied to it; the direction of the cut is radial. The two halves of the zone are detached from each other, as soon as their weight exceeds the resistance of the part which remains to be sawn.
The adjustment of the prisms in the frames, involves an operation which is not without risk. Much care is required in handling the sharp arrises of the glass, which are very acute and delicate and at the same time lie in a curved direction, which makes them liable to be splintered in the hands of unskilful persons.
With the exception of the plane vertical surfaces of the annular lenses, and the central band and rings of the dioptric belts of fixed lights, which are ground by means of vertical rubbers with a reciprocating movement, every other plane surface is executed by hand on a flat table.
| 8 | parts Swedish pitch. |
| 1 | do. of wood ashes. |
The whole is heated in an iron pot until fully liquified and thoroughly mixed. This cement is used almost in a state of ebullition, so that it cannot be handled without the precaution of continually dipping the hands in cold water.
| 12 | parts | white lead. |
| 1 | do. | minium or red lead. |
| 5 | do. | boiled lintseed oil. |
[367]
The whole is pounded on an iron table by means of a flat mullet, like that used by painters (fig. 112), whose grinding surface is a b, and c the knob for the hand. This cement is applied liquid so as to offer no resistance to the close union of the pieces, which it is intended to unite.
Fig. 112.
| 12 | parts | white lead. |
| 3 | do. | whiting. |
| 1 | do. | minium. |
| 4 | do. | boiled lintseed oil. |
This last composition differs from the former only in the introduction of whiting, which, while like minium it has a desiccative property, gives more body to the cement and prevents the formation of cracks. The oil is also decreased in quantity, as the cement must be used in a more compact state. The trituration of this cement is performed by means of a cylindric iron roller a b, with a centre-spoke c d for the hand (fig. 113).
Fig. 113.
It is essential for the production of good cement, that the mixture of the ingredients be complete.
The expense of the various parts of the Dioptric apparatus is as follows: Great lens of first order, L.58 (8 of which are required); pyramidal lens and mirror, L.14, 12s. (8 of which are required); catadioptric cupola, L.480; catadioptric rings below lenses, L.360; pannel of dioptric belt for fixed light of first order, L.56 (of which 8 are required for the whole circle); apparatus of fourth order, for a fixed light, for whole horizon, L.128; apparatus of sixth order, for whole horizon, L.44. The expense of the mechanical lamp of the first order with four wicks, as made for the Scotch Lighthouses by Mr John Milne of Edinburgh, is L.30.
[368]
Fig. 114.
Fig. 115.
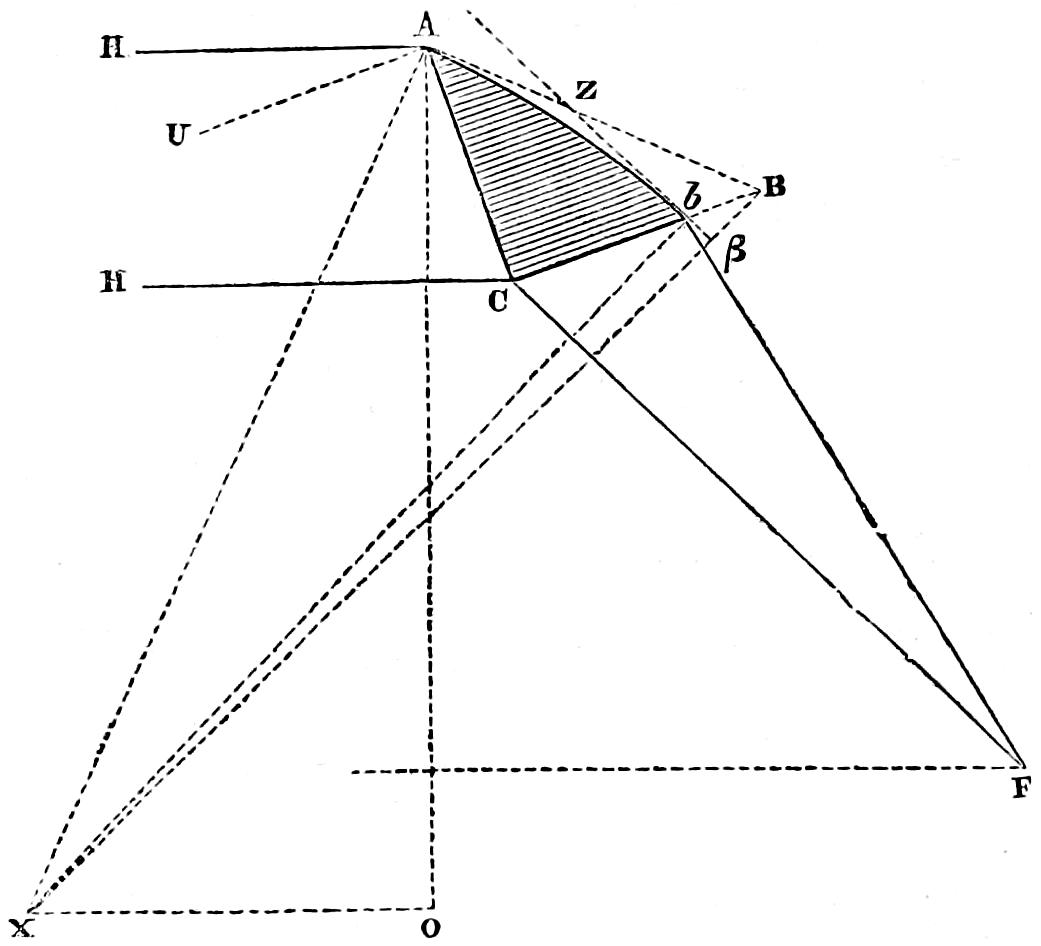
Fig. 116.
Fig. 117.
| Note.—The Six co-ordinates of the Generating Triangle of each Zone in these Tables have the Focus of the Principal Lenses of the System for their origin; it being considered more convenient, in executing the necessary protractions, preparatory to the construction of the grinding apparatus, at once to refer the whole of the grinding machinery to the axis of the apparatus. To prevent the appearance of any inconsistency, however, it is proper to mention, that the radiant points of the series of Zones, do not exactly coincide with the Focus of the Lenses nor with each other; and that to avoid the parallax which the distance of the radiant points from the origin of the co-ordinates would occasion, it is necessary to make some corrections upon the linear dimensions, so as to find the line corresponding to the angles θ, ξ, and the distance Δ. In the Hyperpyral series, which stands above the flame, the Zones have the radiant point 10 millimetres above the Focus of the Lenses, and each y of this series, therefore, requires a reduction of that quantity; while the x remains unchanged. In the Hypopyral series, which stands below the flame, the Focus or radiant points of each Zone, varies its place in the flame, moving upwards as the Zone is lower, so that the line joining the Zones and the Foci, revolves as a radius vector round a point between them. In this way, the x’s remain unaltered; but the y’s will be lengthened successively by the addition of 10, 14, 19, 25, 32, and 40 millimetres. As these Tables contain the dimensions of Zones which are intended as an addition to the apparatus of Fresnel, I have adopted the metric scale, so as to render them at once applicable to the existing protractions of that system. It is only necessary to add, that the conversion of millimetres into imperial inches, is easily effected by adding the log. millimetres to the log. ̅2·59516, the sum being the log. of the equivalent of the first term in imperial inches. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| θ | ξ | BCA, | ABC, | BAC, | BA, | BC, | AC, | Co-ordinates of the Apices of the Generating Triangle, in Millimetres, having the Axis of the System cut by the horizontal plane of the focus of the Annular Lenses, for its origin. (Fig. 116.) | Inclination of the Sides of the Generating Triangle to the Vertical Axis of the System. (Fig. 117.) | AB, Reflecting Surfaces (convex). (Fig. 115.) | AC, Outer Refracting Surfaces (concave). | BC, Inner Refracting Surfaces (convex). | Δ, | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No. of Zone. |
Inclination of Ray FC to the Vertical Axis of the System. |
Incidence of Ray FC on Side BC of Zone. |
Obtuse Angle of the Generating Triangle of the Zone. |
Angle of Generating Triangle of Zone. |
Angle of Generating Triangle of Zone. |
Reflecting Side of Zone in Millimetres being Chord of the Arc b A. |
Inner Refracting Side of Zone in Millimetres. |
Outer Refracting Side of Zone in Millimetres. |
Ay | Ax | By | Bx | Cy | Cx | Inclination of AB. |
Inclination of BC. |
Inclination of AC. |
Radius of Curvature in Millimetres, XA or X b. |
Horizontal distance of centre of curvature X from the axis of the System in Millimetres = OX. |
Vertical distance of centre of curvature X below the outer arris of the Zone at A in Millimetres = OA. |
Inclination of the Two Radii in A and B. |
Inclination of the Outer Radius in A to the Vertex. |
Radius of Curvature in Millimetres. |
Horizontal distance of centre of curvature from the axis of the System in Millimetres. |
Vertical distance of centre of curvature above the outer arris of the Zone at A in Millimetres. |
Inclination of the Radii in A and C. |
Inclination of the Outer Radius at A to the Vertex. |
Radius of Curvature in Millimetres. |
Horizontal distance of centre of curvature from the axis of the System in Millimetres. |
Vertical distance of centre of curvature below the outer arris of the Zone at A in Millimetres. |
Inclination of the Radii in C and B. |
Inclination of the Outer Radius in C to the Vertex. |
Distance of C from the Focus for the Zones, in Millimetres = FC. |
No. of Zone. |
|||||||||||||||||||||||||||||||
| (Fig. 114.) | (Fig. 114.) | (Fig. 114.) | (Fig. 114.) | (Fig. 114.) | (Fig. 115.) | (Fig. 115.) | (Fig. 115.) | (Fig. 114.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ||||||||||||||||||||||||
| HYPER- PYRAL SERIES OF ZONES. |
- | 1 | 60 | 45 | 38 | 44 | 06 | 09 | 117 | 26 | 40 | 31 | 48 | 10 | 30 | 45 | 10 | 160·331 | 92·379 | 95·209 | 593·369 | 986·260 | 551·481 | 831·497 | 525·000 | 920·000 | 74 | 51 | 19 | 73 | 20 | 31 | 44 | 06 | 09 | 8750·19 | 3194·76 | 8466·88 | 1 | 02 | 59 | 14 | 38 | 11 | 4000·00 | 3825·31 | 2817·77 | 1 | 21 | 50 | 45 | 12 | 56 | 4000·00 | 2021·19 | 3777·07 | 1 | 19 | 24 | 15 | 58 | 47 | 1054·34 | 1 | |
| 2 | 56 | 55 | 38 | 41 | 28 | 10 | 116 | 00 | 42 | 32 | 32 | 01 | 31 | 27 | 17 | 155·430 | 90·249 | 93·011 | 663·063 | 957·410 | 617·423 | 808·832 | 593·369 | 895·816 | 72 | 55 | 27 | 74 | 32 | 32 | 41 | 28 | 10 | 8253·90 | 3306·80 | 7909·94 | 1 | 04 | 45 | 16 | 32 | 11 | ... | 3923·65 | 2683·55 | 1 | 19 | 56 | 47 | 51 | 52 | ... | 1918·37 | 3797·40 | 1 | 17 | 34 | 14 | 48 | 41 | 1069·02 | 2 | |||
| 3 | 53 | 05 | 38 | 38 | 48 | 29 | 114 | 31 | 20 | 33 | 17 | 30 | 32 | 11 | 10 | 151·551 | 88·729 | 91·434 | 734·313 | 926·908 | 684·958 | 783·619 | 663·063 | 869·605 | 70 | 59 | 39 | 75 | 42 | 51 | 38 | 48 | 29 | 7850·30 | 3411·75 | 7446·67 | 1 | 06 | 22 | 18 | 27 | 11 | ... | 4015·06 | 2542·31 | 1 | 18 | 34 | 50 | 32 | 14 | ... | 1813·60 | 3815·77 | 1 | 16 | 16 | 13 | 39 | 01 | 1087·52 | 3 | |||
| 4 | 49 | 15 | 38 | 36 | 07 | 09 | 112 | 58 | 40 | 34 | 04 | 36 | 32 | 56 | 44 | 148·580 | 87·768 | 90·424 | 807·357 | 894·222 | 754·267 | 755·451 | 734·313 | 840·920 | 69 | 03 | 53 | 76 | 51 | 31 | 36 | 07 | 09 | 7527·08 | 3514·22 | 7056·39 | 1 | 07 | 51 | 20 | 22 | 11 | ... | 4098·54 | 2394·23 | 1 | 17 | 42 | 53 | 14 | 00 | ... | 1707·55 | 3831·95 | 1 | 15 | 26 | 12 | 30 | 46 | 1109·85 | 4 | |||
| 5 | 45 | 25 | 38 | 33 | 24 | 19 | 111 | 23 | 00 | 34 | 53 | 07 | 33 | 43 | 53 | 146·444 | 87·332 | 89·947 | 882·445 | 858·858 | 825·547 | 723·921 | 807·357 | 809·337 | 67 | 08 | 12 | 77 | 58 | 41 | 33 | 24 | 19 | 7275·23 | 3617·56 | 6730·66 | 1 | 09 | 12 | 22 | 17 | 11 | ... | 4173·08 | 2239·64 | 1 | 17 | 18 | 55 | 57 | 02 | ... | 1599·72 | 3846·04 | 1 | 15 | 04 | 11 | 23 | 47 | 1136·14 | 5 | |||
| 6 | 41 | 35 | 38 | 30 | 40 | 05 | 109 | 44 | 32 | 35 | 42 | 57 | 34 | 32 | 31 | 145·087 | 87·403 | 89·986 | 959·847 | 820·325 | 899·011 | 688·608 | 882·445 | 774·426 | 65 | 12 | 36 | 79 | 04 | 27 | 30 | 40 | 05 | 7082·17 | 3723·81 | 6459·63 | 1 | 10 | 25 | 24 | 12 | 11 | ... | 4237·70 | 2078·82 | 1 | 17 | 20 | 58 | 41 | 15 | ... | 1489·62 | 3858·14 | 1 | 15 | 08 | 10 | 17 | 59 | 1166·57 | 6 | |||
| 7 | 37 | 45 | 38 | 27 | 54 | 34 | 108 | 03 | 30 | 36 | 34 | 01 | 35 | 22 | 29 | 144·481 | 87·977 | 90·536 | 1039·852 | 778·108 | 974·899 | 649·051 | 959·847 | 735·730 | 63 | 17 | 03 | 80 | 08 | 56 | 27 | 54 | 34 | 6944·09 | 3835·23 | 6234·93 | 1 | 11 | 31 | 26 | 07 | 11 | ... | 4291·45 | 1912·18 | 1 | 17 | 48 | 61 | 26 | 32 | ... | 1376·71 | 3868·30 | 1 | 15 | 36 | 9 | 13 | 16 | 1201·46 | 7 | |||
| 8 | 33 | 55 | 38 | 25 | 07 | 52 | 106 | 20 | 06 | 37 | 26 | 11 | 36 | 13 | 43 | 144·609 | 89·060 | 91·604 | 1122·784 | 731·645 | 1053·471 | 604·730 | 1039·852 | 692·742 | 61 | 21 | 35 | 81 | 12 | 14 | 25 | 07 | 52 | 6857·03 | 3954·67 | 6052·36 | 1 | 12 | 30 | 28 | 02 | 11 | ... | 4333·30 | 1740·12 | 1 | 18 | 44 | 64 | 12 | 46 | ... | 1260·38 | 3876·59 | 1 | 16 | 32 | 8 | 09 | 30 | 1241·16 | 8 | |||
| 9 | 30 | 05 | 38 | 22 | 20 | 07 | 104 | 34 | 36 | 38 | 19 | 23 | 37 | 06 | 01 | 145·476 | 90·671 | 93·209 | 1209·000 | 680·322 | 1135·025 | 555·059 | 1122·784 | 644·900 | 59 | 26 | 08 | 82 | 14 | 29 | 22 | 20 | 07 | 6817·87 | 4081·70 | 5902·53 | 1 | 13 | 20 | 29 | 57 | 11 | ... | 4362·26 | 1563·10 | 1 | 20 | 06 | 66 | 59 | 50 | ... | 1139·94 | 3883·03 | 1 | 17 | 56 | 7 | 06 | 33 | 1286·15 | 9 | |||
| 10 | 26 | 15 | 38 | 19 | 31 | 25 | 102 | 47 | 12 | 39 | 13 | 27 | 37 | 59 | 21 | 147·089 | 92·843 | 95·384 | 1298·900 | 623·433 | 1219·892 | 499·354 | 1209·000 | 591·556 | 57 | 30 | 46 | 83 | 15 | 47 | 19 | 31 | 25 | 6824·46 | 4226·67 | 5795·68 | 1 | 14 | 05 | 31 | 52 | 11 | ... | 4377·24 | 1381·63 | 1 | 21 | 58 | 69 | 47 | 36 | ... | 1014·67 | 3887·66 | 1 | 19 | 48 | 6 | 04 | 19 | 1336·99 | 10 | |||
| 11 | 22 | 25 | 38 | 16 | 41 | 54 | 100 | 58 | 10 | 40 | 07 | 14 | 38 | 54 | 36 | 145·361 | 93·000 | 95·413 | 1390·290 | 559·378 | 1308·183 | 439·428 | 1288·900 | 531·963 | 55 | 36 | 30 | 84 | 16 | 16 | 16 | 41 | 54 | 6880·52 | 4385·63 | 5718·52 | 1 | 12 | 37 | 33 | 47 | 11 | ... | 4376·72 | 1194·94 | 1 | 22 | 00 | 72 | 37 | 06 | ... | 884·95 | 3893·00 | 1 | 19 | 56 | 5 | 03 | 46 | 1394·36 | 11 | |||
| 12 | 18 | 42 | 02 | 13 | 56 | 26 | 99 | 10 | 50 | 40 | 59 | 53 | 39 | 49 | 17 | 143·362 | 93·000 | 95·271 | 1482·755 | 490·169 | 1398·007 | 374·538 | 1390·290 | 467·217 | 53 | 45 | 43 | 85 | 14 | 24 | 13 | 56 | 26 | 6980·89 | 4558·83 | 5672·64 | 1 | 10 | 36 | 35 | 38 | 59 | ... | 4360·70 | 1009·41 | 1 | 21 | 12 | 75 | 22 | 58 | ... | 752·78 | 3897·32 | 1 | 19 | 56 | 4 | 05 | 38 | 1457·22 | 12 | |||
| 13 | 15 | 06 | 03 | 11 | 16 | 04 | 97 | 26 | 07 | 41 | 51 | 03 | 40 | 42 | 49 | 141·379 | 93·000 | 95·127 | 1576·048 | 415·991 | 1488·972 | 304·611 | 1482·755 | 397·403 | 51 | 58 | 53 | 86 | 10 | 02 | 11 | 16 | 04 | 7123·05 | 4747·24 | 5654·92 | 1 | 08 | 15 | 37 | 26 | 59 | ... | 4329·31 | 828·19 | 1 | 21 | 46 | 78 | 03 | 02 | ... | 618·37 | 3901·10 | 1 | 19 | 56 | 3 | 10 | 00 | 1525·43 | 13 | |||
| ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ° | ′ | ″ | ||||||||||||||||||||||||
| HYPO- PYRAL SERIES. |
- | 1 | 59 | 49 | 16 | 43 | 27 | 36 | 117 | 05 | 56 | 31 | 58 | 37 | 30 | 55 | 27 | 159·369 | 92·000 | 94·806 | 593·815 | 985·212 | 550·915 | 831·725 | 525·000 | 920·000 | 74 | 23 | 03 | 73 | 38 | 20 | 43 | 27 | 36 | 8674·74 | 3243·48 | 8375·64 | 1 | 03 | 09 | 15 | 05 | 22 | 4000·00 | 3855·83 | 2785·60 | 1 | 21 | 28 | 45 | 51 | 40 | 4000·00 | 2002·52 | 3781·91 | 1 | 19 | 04 | 15 | 42 | 08 | —— | 1 | |
| 2 | 55 | 48 | 55 | 40 | 42 | 01 | 115 | 35 | 07 | 32 | 44 | 43 | 31 | 40 | 09 | 158·051 | 92·000 | 94·783 | 682·731 | 981·810 | 634·862 | 831·183 | 610·872 | 920·000 | 72 | 22 | 10 | 74 | 53 | 06 | 40 | 42 | 01 | 8419·60 | 3456·44 | 8047·72 | 1 | 04 | 31 | 17 | 05 | 32 | ... | 3983·21 | 2644·16 | 1 | 21 | 28 | 48 | 37 | 15 | ... | 1918·55 | 3801·51 | 1 | 19 | 04 | 14 | 27 | 22 | —— | 2 | |||
| 3 | 51 | 48 | 33 | 37 | 54 | 32 | 114 | 00 | 31 | 33 | 28 | 16 | 32 | 27 | 13 | 156·592 | 92·000 | 94·719 | 779·464 | 978·917 | 726·831 | 830·694 | 704·730 | 920·000 | 70 | 21 | 45 | 76 | 05 | 59 | 37 | 54 | 32 | 8278·82 | 3685·41 | 7823·68 | 1 | 05 | 01 | 19 | 05 | 13 | ... | 4104·84 | 2494·82 | 1 | 21 | 24 | 51 | 24 | 46 | ... | 1836·22 | 3818·93 | 1 | 19 | 04 | 13 | 14 | 29 | —— | 3 | |||
| 4 | 47 | 51 | 11 | 35 | 07 | 32 | 112 | 23 | 53 | 34 | 20 | 23 | 33 | 15 | 44 | 155·083 | 92·000 | 94·619 | 885·046 | 974·441 | 827·926 | 830·261 | 807·657 | 920·000 | 68 | 23 | 16 | 77 | 16 | 21 | 35 | 07 | 32 | 8252·95 | 3941·89 | 7701·00 | 1 | 04 | 36 | 21 | 04 | 24 | ... | 4218·56 | 2340·02 | 1 | 21 | 20 | 54 | 11 | 48 | ... | 1756·33 | 3834·20 | 1 | 19 | 04 | 12 | 04 | 07 | —— | 4 | |||
| 5 | 43 | 59 | 40 | 32 | 23 | 06 | 110 | 46 | 32 | 35 | 08 | 23 | 34 | 05 | 05 | 153·489 | 92·000 | 94·488 | 1000·663 | 970·608 | 939·385 | 829·882 | 920·871 | 920·000 | 66 | 28 | 11 | 78 | 23 | 26 | 32 | 23 | 06 | 8335·86 | 4228·06 | 7673·05 | 1 | 03 | 18 | 23 | 00 | 10 | ... | 4322·95 | 2182·17 | 1 | 21 | 12 | 56 | 56 | 18 | ... | 1679·85 | 3847·38 | 1 | 19 | 04 | 10 | 57 | 02 | —— | 5 | |||
| 6 | 40 | 16 | 34 | 29 | 43 | 19 | 109 | 10 | 04 | 35 | 55 | 37 | 34 | 54 | 18 | 151·863 | 92·000 | 94·334 | 1127·665 | 966·771 | 1062·591 | 829·557 | 1045·740 | 920·000 | 64 | 37 | 37 | 79 | 26 | 45 | 29 | 43 | 19 | 8522·64 | 4549·97 | 7732·80 | 1 | 01 | 15 | 24 | 51 | 43 | ... | 4416·91 | 2023·99 | 1 | 21 | 04 | 59 | 36 | 09 | ... | 1607·39 | 3858·56 | 1 | 19 | 04 | 9 | 53 | 43 | —— | 6 | |||
[369]
The Commissioners of the Northern Lighthouses hereby give notice, that a Lighthouse has been erected upon the Skerryvore Rock, which lies off the Island of Tyree, in the county of Argyll, the Light of which will be exhibited on the Night of the 1st February 1844, and every Night thereafter, from sunset to sunrise.
A specification of the bearings of the Lighthouse and character of the Light will be found on the next page.
And the Commissioners hereby further give notice, that by virtue of a Warrant from the Queen in Council, of date the 13th December 1843, the following Tolls will be levied for voyages in respect of which benefit will be derived from this Light, viz., from every British Vessel (the same not belonging to Her Majesty, or being navigated wholly in ballast), and for every Foreign Vessel which, by any Act of Parliament, Order in Council, Convention, or Treaty, shall be privileged to enter the Ports of the United Kingdom of Great Britain and Ireland, upon paying the same duties of tonnage as are paid by British Vessels (the same not being navigated wholly in ballast), the Toll of One Penny per Ton of the Burden of every such Vessel; and for every Foreign Vessel not so privileged, the Toll of Two Pence per Ton.
By Order of the Commissioners,
(Signed)C. Cuningham,
(Signed)Alex. Cuningham,
}Joint Secs.
Edinburgh, 23d December 1843.
[370]
The following is a Specification of the Position of the Lighthouse, and the Appearance of the Light, by Mr Alan Stevenson, Engineer to the Commissioners.
The Skerryvore Rock lies off the Island of Tyree, in Lat. 56° 19′ 22″ N.; Long. 7° 6′ 32″ W.
By Compass, the Lighthouse bears from Barrahead Lighthouse S. ¹⁄₄ E., distant 33 nautic miles; from Hynish Point, in Tyree, WSW. ¹⁄₂ W., distant 10¹⁄₃ miles; from Iona Island, WNW. ³⁄₄ N., distant 20 miles; from Rhinns of Islay Lighthouse, N. ¹⁄₄ E., distant 44 miles; and from Innistrahull Lighthouse in Ireland, NE. by N., distant 53¹⁄₂ miles.
Owing to the distance to which the foul ground extends on every side of the rock on which the Lighthouse is placed, and the weight of sea which breaks on the shallow ground all round it, it is necessary to give the Light a wide berth. The better to enable seamen to judge of this, their attention is called to the prefixed Chart,[87] which exhibits the relative position of the Skerryvore Rock, and the various dangers around it. In particular, it is necessary to notice the position of those rocks which lie seaward of the Lighthouse, viz. Mackenzie’s Rock, about 3 miles W. by S. ¹⁄₄ S. from the Lighthouse; Stevenson’s, 2¹⁄₄ miles W. ¹⁄₂ N.; and Fresnel’s, which lies between these two Rocks. To the left of the prefixed Chart is a small diagram, which exhibits the position of the Skerryvore Rock in reference to the principal landmarks above noticed.
The Skerryvore Light will be known to mariners as a Revolving Light, producing a Bright Flash once every minute. The Lantern, which is open all round, is elevated 150 feet above the level of the sea. In clear weather the flashes of the Light will be seen at the distance of six leagues, and at lesser distances according to the state of the atmosphere; and to a near observer, in favourable circumstances, the Light will not wholly disappear between the flashes.
[371]
[385]
The letters (see Plate IV.) D E F D represent a cast-iron cylinder, which is firmly bolted at the projecting flanges G to the rock where the experiments are wanted. This cylinder has a flange at D D. L L is a door, which is opened when the observation is to be read off. A A is of iron, and forms a circular plate or disc, on which the sea impinges. Fastened to the disc are four guide-rods B B B B. These rods pass through a circular plate C C (which is screwed down to the flange D D), and also through holes in the bottom E F. Within the cylinder there is attached to the plate C C a powerful steel spring, to the other or free end of which is fastened the small circular plate K K, which again is secured to the guide-rods B B B B. There are also rings of leather T T, that slide on the guide-rods, and serve as indices for registering how far the rods are pushed through the holes in the bottom; or, in other words, how much the spring has been drawn out or lengthened by the force of the sea acting upon the plate or disc A A. The object of having four leathern rings, where one might have answered the purpose, was merely that they might serve as a check upon each other; and so perfectly did they answer the purpose intended, that in every instance they were found equidistant from the bottom of the cylinder; proving thereby, that after the recoil of the spring, they had all kept their places. The guide-rods are graduated, so as to enable the observer to note exactly the quantity that the spring has yielded.
This instrument, which may, perhaps, be not improperly termed a Marine Dynamometer, is, therefore, a self-registering apparatus which indicates the maximum force of the waves. In the graduation of the instrument, the power of the spring is ascertained by carefully loading the disc with weights, so that when the quantity that the spring has yielded by the action of the sea is known, the pressure due to the area of the disc exposed is known also. The discs employed were from 3 to 9 inches diameter, but[386] generally 6 inches, and the powers of the springs varied from 10 lb. to about 50 lb. for every ¹⁄₈ inch of elongation. Their respective effects were afterwards reduced to a value per square foot. The instrument was generally placed so as to be immersed at about three-fourths tide, and in such situations as would afford a considerable depth of water. It is not desirable to have the instrument placed at a much lower level, as it has not unfrequently happened during a gale, that for days together no one could approach it to read off the result and readjust the indices to zero. It must, however, at the same time be remarked, that it is in most situations almost impossible to receive the force unimpaired, as the waves are more or less broken by hidden rocks or shoal ground before they reach the instrument.
In connection with the apparatus above described, a graduated pole was erected on an outlying sunken rock, for the purpose of ascertaining the height of the waves; but the observations were not of so satisfactory a nature as could have been desired, and the poles soon worked loose from their attachments, and disappeared.
With the instrument which has been explained, I entered upon the following train of observations:—
In 1842 several observations were made on the waves of the Irish Sea at the island of Little Ross, lying off the Bay of Kirkcudbright. Since April 1843 till now, continued observations have been made on the Atlantic at the Skerryvore and neighbouring rocks lying off the island of Tyree, Argyllshire; and in 1844 a series of observations was begun on the German Ocean at the Bell Rock. It will be seen, that in selecting these localities a varied exposure has been embraced, comprising the comparatively sheltered Irish Sea, the more exposed eastern shore of Scotland, and the wild Rocks of Skerryvore, which are open to the full fury of the Atlantic, the far distant shores of North America being the nearest land on the west.
Referring for more full information to the tables of experiments which are given at the end of this paper, it will be sufficient in this place to state generally the following as the results obtained.
In the Atlantic Ocean, according to the observations made at the Skerryvore rocks, the average of results for five of the summer months during the years 1843 and 1844, is 611 lb. per square foot. The average results for six of the winter months (1843 and 1844), is 2086 lb. per square foot, or thrice as great as in the summer months.
The greatest result yet obtained at Skerryvore was during the heavy[387] westerly gale of 29th March 1845, when a pressure of 6083 lb. per square foot was registered. The next highest is 5323 lb.
In the German Ocean, according to the observations made at the Bell Rock, the greatest result yet obtained is 3013 lb. per square foot.
It thus appears, that the greatest effect of the sea, which has been observed, is that of the Atlantic at Skerryvore, which is nearly equal to three tons per square foot.
These experiments, amounting to 267 in number, and on the Atlantic alone, extending over 23 months continuously, are not intended to prove anything farther than the simple fact, that the sea has been known to exert a force equivalent to a pressure of three tons per square foot, however much more.
It is proper, however, to observe, that there may be some objection to referring the action of the sea to a statical value. Although the instrument might perhaps be made capable of giving a dynamical result, it was considered unnecessary, in these preliminary experiments, to do anything more than represent the maximum pressure registered by the spring, because the effects of the waves may, from supposing them to have continuity of action, be perhaps regarded as similar to a statical pressure, rather than to the impact of a hard body. The near coincidence, or indeed almost perfect agreement of the results of the experiments made with different instruments, goes far to shew that the waves act in very much the same manner as a pressure, although both pressure and impact must obviously enter into their effect. In the experiments, begun February 1844, and given at the end of the paper, the three instruments had not only different areas of discs, but very different powers of springs, and yet the results were almost identical. Now, the same force, supposing the waves to act like the impact of a hard body, would, in the Marine Dynamometer, have assumed very different statical values, according to the spaces in which that force was expended or developed; so that with the same force of impact, the indication of a weak spring would be less than that of a stronger.
In future experiments it may be interesting, however, to test the springs dynamically, by means of the impact of a heavy body dropped from a given height upon the plate or disc of the instrument. In some experiments lately made in this way, by dropping a cannon-ball upon the disc, it appeared, that, within the limits of the experiments, there was for each individual spring a ratio between the value registered by the leathern index and the calculated momentum of the impinging body. These ratios were, of[388] course, found to vary in springs of different power, and to be constant only for springs of the same power. Did the waves, therefore, act by a sudden finite impact, like the cannon-ball employed in this instance, we could scarcely have found such harmony between the results of instruments with different springs, as the experiments alluded to afford. At the same time, the result cannot, perhaps, be in strictness considered correct; but, from the elongation of the spring being very small, the results may be regarded as practically correct,—the more so when we find so remarkable a coincidence of results as that alluded to.
Experiments.—With reference to the following experiments I have only to observe, that those which were made at Little Ross, upon the Irish Sea, cannot, from the unusual fineness of the weather at the time, be regarded as affording a true value of the effects of a hard gale in these seas. Of the others it is to be noticed, that where two or three instruments were for some time employed as a check upon each other, and only one or two readings are given, the want has occurred either from the instruments being under repair, or being difficult of access in stormy weather, or during neap tides. It often happened also, in consequence of the springs proving too weak, when new ones had to be made, or the area of the disc reduced. Registers of the state of the weather, apparent height of spray, &c., were generally kept; but it was not considered necessary to complicate the Tables by inserting these, excepting in one or two instances.
[389]
| Dates. | lbs. to a Square Foot. | ||||
|---|---|---|---|---|---|
| Observations at Little Ross. | |||||
| 1842. | |||||
| April | 25 | 15 | |||
| 28 | 51 | ||||
| June | 1 | 36 | |||
| 4 | 81·5 | ||||
| 20 | 86·5 | ||||
| 24 | 840·0 | ||||
| 25 | 458·0 | ||||
| July | 25 | 380·0 | |||
| Aug. | 2 | 570·0 | |||
| 5 | 665·0 | ||||
| 6 | 380·0 | ||||
| 9 | 380·0 | ||||
| The Observations at the Skerryvore Rock, and the neighbouring Island of Tyree, distant 13 miles from the Skerryvore, are as follows:— | |||||
| 1843. | |||||
| April | 24 | 455 | |||
| 25 | 707 | ||||
| May | 7 | 243 | |||
| 11 | 182 | ||||
| 12 | 243 | ||||
| 16 | 364 | ||||
| 20 | - | 495 | |||
| 476 | |||||
| June | 3 | 182 | |||
| 4 | 519 | ||||
| 7 | 428 | ||||
| 8 | 855 | ||||
| 9 | 173 | ||||
| July | 2 | 476 | |||
| 3 | - | 723 | |||
| 866 | |||||
| 30 | 433 | ||||
| Aug. | 9 | 346 | |||
| 22 | 723 | ||||
| 30 | 389 | ||||
| Sept. | 5 | 866 | |||
| 21 | 952 | ||||
| Oct. | 5 | 1535 | |||
| 6 | 1606 | ||||
| Nov. | 18 | 1711 | |||
| 19 | 1497 | ||||
| 27 | 1497 | ||||
| 29 | 2353 | ||||
| Dec. | 5 | 2674 | |||
| 8 | - | 3421 | |||
| At least | |||||
| 14 | 2460 | ||||
| 26 | 1947 | ||||
| In January, two instruments were placed beside each other, but not set parallel. These instruments had springs of different power, the one being about double that of the other, and one had a disc of 3 inches diameter, the other 6 inches. | |||||
| 1844. | |||||
| Jan. | 6 | 962 | |||
| 928 | |||||
| 7 | 2353 | ||||
| 357 | |||||
| 9 | 1925 | ||||
| 1000 | |||||
| 10 | 826 | ||||
| 1000 | |||||
| Both instruments set parallel. | |||||
| 16 | 424 | ||||
| 427 | |||||
| Another instrument was placed beside them, but the two marked thus* were found to be too weak, as the leathers were found flattened, and one of the instruments was broken, and was not repaired till the 15th February. | |||||
| 28 | 3422 | * | |||
| 2285 | * | ||||
| 3313 | |||||
| Feb. | 2 | 429 | |||
| 457 | |||||
| 3 | 429 | ||||
| 457 | |||||
| 13 | 214 | ||||
| 228 | |||||
| 15 | 321 | ||||
| 280 | |||||
| 321 | |||||
| 16 | 428 | ||||
| 402 | |||||
| 343 | |||||
| 24 | 1284 | ||||
| 1364 | |||||
| 685 | |||||
| 26 | 2032 | ||||
| 2068 | |||||
| 399 | |||||
| 27 | 321 | ||||
| 321 | |||||
| 342 | |||||
| March | 4 | 3316 | |||
| 3369 | |||||
| 3427 | |||||
| 7 | 1069 | ||||
| 963 | |||||
| 913 | |||||
| 10 | 1925 | ||||
| 1925 | |||||
| 1713 | |||||
| 11 | 535 | ||||
| 481 | |||||
| 456 | |||||
| 12 | 3316 | ||||
| 4011 | |||||
| 2970 | |||||
| 13 | 1142 | ||||
| 1283 | |||||
| 1283 | |||||
| April | 10 | 457 | |||
| 428 | |||||
| 481 | |||||
| 11 | 800 | ||||
| 12 | 343 | ||||
| 321 | |||||
| 14 | 571 | ||||
| 535 | |||||
| 16 | 571 | ||||
| 642 | |||||
| 481 | |||||
| 17 | 800 | ||||
| 856 | |||||
| 862 | |||||
| 18 | 571 | ||||
| 481 | |||||
| 19 | 800 | ||||
| 535 | |||||
| 481 | |||||
| 22 | 913 | ||||
| 482 | |||||
| 962 | |||||
| 24 | 1942 | ||||
| 1604 | |||||
| 1370 | |||||
| 25 | 1283 | ||||
| 343 | |||||
| 321 | |||||
| 27 | 457 | ||||
| 481 | |||||
| - | Night | 800 | |||
| tide | |||||
| 642 | |||||
| 30 | 229 | ||||
| 241 | |||||
| May | 15 | 343 | |||
| 14 | 481 | ||||
| June | 6 | 571 | |||
| 15 | 1828 | ||||
| July | 11 | 1028 | |||
| 13 | 457 | ||||
| 18 | 914 | ||||
| 23 | 1532 | ||||
| 25 | 571 | ||||
| 26 | 971 | ||||
| 27 | 457 | ||||
| 28 | 1142 | ||||
| 29 | 286 | ||||
| 30 | 914 | ||||
| 31 | 1028 | ||||
| Aug. | 1 | 571 | |||
| 7 | 914 | ||||
| 13 | 914 | ||||
| 14 | 914 | ||||
| 21 | 800 | ||||
| 30 | 1713 | ||||
| Sept. | 12 | 1028 | |||
| 14 | 914 | ||||
| 20 | 457 | ||||
| 23 | 1142 | ||||
| 25 | 685 | ||||
| 30 | 1599 | ||||
| Oct. | 2 | 2399 | |||
| 3 | 1485 | ||||
| 4 | 1828 | ||||
| 11 | 3427 | [88] | |||
| 14 | 1599 | ||||
| 19 | 1599 | ||||
| 20 | 2513 | ||||
| 22[390] | 800 | ||||
| 24 | 1827 | ||||
| 28 | 1485 | ||||
| 29 | 457 | ||||
| Nov. | 2 | 1942 | |||
| 10 | 1028 | ||||
| 14 | 1257 | ||||
| 15 | 2056 | ||||
| 16 | 2056 | ||||
| 22 | 2627 | ||||
| 23 | 3427 | ||||
| 27 | 3199 | ||||
| 28 | 4112 | ||||
| Dec. | 7 | 1369 | |||
| 9 | 2738 | ||||
| 10 | 1825 | ||||
| 13 | 1925 | ||||
| 14 | 1027 | ||||
| 15 | 1764 | ||||
[88] On this occasion, 14 stones were slightly moved, and 14 scattered, all of which had been built into the round-head or end of Hynish Pier, which was still in an unfinished state, and a Dynamometer which was attached to the Pier, registered on this occasion 2557 lb. These stones weighed from 1 to 1¹⁄₂ tons, and exposed, when built into the wall, about two square feet of surface. The stone to which the instrument was fixed was turned upside down, although it weighed about 1¹⁄₄ ton = 2800 lb.
A more exposed point of the Skerryvore Rock was at this time chosen for experiment; and with the view of ascertaining the effect of the waves at different heights upon the rock, two instruments were fixed, the one (No. I.) several feet lower, and about 40 feet seaward of the other (No. II.). It was observed, that about half-flood the force of the waves was a good deal expended before they reached the place where No. I. was placed, from there being so little water on the rocks outside; whereas when the tide was higher, the waves were, from the greater depth of water, not so much broken when they reached No. II. The results of the Marine Dynamometer shew generally about twice the force at No. II. as at No. I.; a result which shews how important it would be to ascertain the relative forces of the waves at different levels upon our breakwaters and other seaworks.
| Date. | Remarks. | No. of Instru- ment. |
Pressure in lbs. per Square Foot. |
|
|---|---|---|---|---|
| 1845. | ||||
| Jan. | 7 | Heavy sea. | I. | 1714 |
| ... | II. | 4182 | ||
| 12 | Very heavy swell. | I. | 2856 | |
| ... | II. | 5032 | ||
| 16 | Heavy ground swell. | I. | 2856 | |
| ... | II. | 4752 | ||
| 22 | A good deal of sea. | I. | 2856 | |
| ... | II. | 5323 | ||
| 28 | Heavy ground swell. | I. | 2627 | |
| ... | II. | 4562 | ||
| Feb. | 5 | Fresh gales. | I. | 856 |
| ... | II. | 3042 | ||
| 21 | ... | I. | 1827 | |
| ... | II. | 3422 | ||
| 24 | Fresh breezes. | I. | 1256 | |
| ... | II. | 3802 | ||
| March | 9 | Ground swell. | I. | 1256 |
| Waves supposed about 10 feet high. | II. | 3041 | ||
| 11 | Short sea. | I. | 1028 | |
| 24 | Heavy sea. | I. | 2281 | |
| Waves supposed about 20 feet high. | II. | 4562 | ||
| 26 | Swell. | I. | 1256 | |
| Waves about 6 feet high. | II. | 3041 | ||
| 29 | Strong gale, with heavy sea, the highest waves supposed 20 feet high, and the spray rose about 70 feet. | I. | 2856 | |
| ... | II. | 6083 | ||
[391]
Register of Observations on the force of the Sea, made at the Bell Rock, German Ocean.
| Dates. | lbs. to a Square Foot. |
|
|---|---|---|
| 1844. | ||
| Sept. | 15 | 853 |
| 20 | 2260 | |
| Oct. | 9 | 3013 |
| ... | 2562 | |
| 26 | 1142 | |
| 27 | 958 | |
| Nov. | 12 | 1680 |
| 13 | 1920 | |
| Dec. | 13 | 1560 |
| 26 | 1439 | |
| 1845. | ||
| Jan. | 7 | 1559 |
| 10 | 1439 | |
| 11 | 1439 | |
| 15 | 1559 | |
| 25 | 959 | |
| 26 | 719 | |
| 27 | 1199 | |
| 30 | 2879 | |
| 31 | 1559 | |
| Feb. | 6 | 2999 |
| 24 | 1199 | |
| 25 | 959 | |
| 27 | 839 | |
| 28 | 1319 | |
| March | 4 | 959 |
| 7 | 1079 | |
| 11 | 1919 | |
| 20 | 2519 | |
| 21 | 2759 | |
| 24 | 1319 | |
| 25 | 959 | |
| 28 | 599 | |
| 30 | 1079 | |
| Name of Light. | Situation of Light. | Number of Lights. |
Appearance of Light. | Distance visible in Nautic Miles. |
Points of Compass within which Light is Visible. |
Height of Lantern in feet above High-water Spring Tides. |
North Latitude. |
West Longitude. |
Date of first Exhibition. |
||
|---|---|---|---|---|---|---|---|---|---|---|---|
| INCHKEITH | Highest Land on the Island of Inchkeith, in Fifeshire | One | Revolving, and appearing in its brightest state once every minute | 18 | All round the Compass | 220 | 56° | 2′ | 3° | 8′ | 1804 |
| ISLE OF MAY | Highest Land on Isle of May, in Fifeshire | One | Fixed | 21 | All round the Compass | 240 | 56° | 11′ | 2° | 33′ | 1816 |
| DO. LEADING LIGHT | Placed about 130 feet below the High Light, and to the NE. by N. of it | One | Fixed | 15 | When seen in ONE line with the High Light, these two Lights bear NE. by N. ¹⁄₄ N., and SW. by S. ¹⁄₄ S., and in this line lead about half a mile to the Eastward of the North Carr Rock. The Lights must on no account be opened to the Westward | 110 | 1844 | ||||
| BELL ROCK | Bell Rock, a sunk reef, 11³⁄₄ miles S. by E. ¹⁄₃ E. off Arbroath, in Forfarshire | One | Revolving, and shewing alternately a red and white light every 2 minutes | 14 | All round the Compass | 90 | 56° | 26′ | 2° | 23′ | 1811 |
| GIRDLENESS | Girdleness, Kincardineshire | Two | Fixed Lights, one above the other | 19 & 16 | From NNE. to WSW. ¹⁄₂ W. Easterly and Southerly | 185 & 115 | 57° | 8′ | 2° | 3′ | 1833 |
| BUCHANNESS | Buchanness, Aberdeenshire | One | Flashing once every 5 seconds | 16 | From N. by E. to SW. by W. Easterly | 130 | 57° | 28′ | 1° | 46′ | 1827 |
| KINNAIRDHEAD | Kinnairdhead, Aberdeenshire | One | Fixed | 15 | From WNW. to SE. Northerly | 120 | 57° | 42′ | 2° | 0′ | 1787 |
| COVESEA SKERRIES | Craighead, Morayshire | One | Revolving, and appearing in its brightest state once every minute. From W. by N. ¹⁄₄ N. to SE. by E. ¹⁄₄ E. the light is of the natural appearance; but from SE. by E. ¹⁄₄ E. to SE. ¹⁄₄ S. it is coloured RED | 18 | From W. by N. ¹⁄₄ N. to SE. ¹⁄₄ S. Northerly | 160 | 57° | 43′ | 3° | 20′ | 1846 |
| CHANONRY POINT | Chanonry Point, Ross-shire | One | Fixed | 11 | From W. ¹⁄₂ N. to N. by E. Southerly | 40 | 57° | 35′ | 4° | 5′ | 1846 |
| CROMARTY POINT | Cromartyshire | One | Fixed and red | 9 | From WNW. to SE. by E. ¹⁄₄ S. Northerly | 50 | 57° | 41′ | 4° | 2′ | 1846 |
| TARBETNESS | Tarbetness, Cromartyshire | One | Intermittent, suddenly bursting into view, and continuing in sight 2¹⁄₂ min., then suddenly eclipsed for half a minute. But within the Moray Frith, in Southerly and South-westerly directions from Tarbetness, the light does not intermit, but is permanently visible | 18 | From SW. ¹⁄₂ W. to W. ¹⁄₂ N. Easterly | 175 | 57° | 51′ | 8° | 48′ | 1830 |
| NOSSHEAD | Nosshead, Caithness-shire (building) | ||||||||||
| DUNNETHEAD | Dunnethead, most northern point of the Mainland of Scotland, Caithness-shire | One | Fixed | 23 | From SE. ¹⁄₂ E. to W. Northerly | 346 | 58° | 40′ | 3° | 21′ | 1831 |
| PENTLAND SKERRIES | Pentland Skerries Island, Orkney | Two | Fixed, and 100 feet apart | 16 & 18 | All round the Compass | 140 & 170 | 58° | 41′ | 2° | 55′ | 1794 |
| START POINT | Start Point, Sanday Island, the most eastern point of Orkney | One | Revolving, and appearing in its brightest state once every minute | 15 | All round the Compass | 100 | 59° | 17′ | 2° | 23′ | 1806 |
| SUMBURGH-HEAD[396- 397] |
The most southern Headland of Zetland | One | Fixed | 22 | From NE. by E. ¹⁄₄ E. to NW. by N. ¹⁄₄ N. Southerly | 300 | 59° | 51′ | 1° | 16′ | 1821 |
| CAPE WRATH | Cape Wrath, north-western Headland of Sutherlandshire | One | Revolving, and shewing alternately a red and white light every 2 minutes | 25 | From SE. ¹⁄₂ E. to SW. by W. Northerly | 400 | 58° | 37′ | 5° | 0′ | 1828 |
| ISLAND GLASS | Island Glass, one of the Harris Isles, Inverness-shire | One | Fixed | 16 | From W. by S. to ENE. ¹⁄₂ E. Southerly | 130 | 57° | 52′ | 6° | 33′ | 1789 |
| BARRAHEAD | Highest land on Bernera Island, Inverness-shire | One | Intermittent, suddenly bursting into view, and continuing in sight 2¹⁄₂ min., then suddenly eclipsed for half a minute | 32 | From N. by E. to ENE. Westerly and Southerly | 680 | 56° | 48′ | 7° | 38′ | 1833 |
| ARDNAMURCHAN | Ardnamurchan Point, Argyleshire (building) | ||||||||||
| LISMORE | Mousedale, small Island off Lismore, Argyleshire | One | Fixed | 15 | From E. to NE. by E. ¹⁄₄ E. Westerly | 103 | 56° | 30′ | 5° | 38′ | 1833 |
| SKERRYVORE[89] | Skerryvore Reef, 12 miles WSW. ¹⁄₂ W. from Tyree Island, with foul ground all round it | One | Revolving, and appearing at its brightest once every minute | 18 | All round the Compass | 150 | 56° | 19′ | 7° | 7′ | 1844 |
| RHINS OF ISLAY | Oversay, small Island off Islay, Argyleshire | One | Flashing once every 5 seconds | 17 | From NNE. to SE. Southerly | 150 | 55° | 41′ | 6° | 29′ | 1825 |
| MULL OF KINTYRE | South-western Headland of Argyleshire | One | Fixed | 22 | From NNE. ¹⁄₂ E. to S. by W. ¹⁄₄ W. Southerly | 297 | 55° | 1′ | 5° | 49′ | 1787 |
| PLADDA | Pladda Isle, off south-east point of Arran, county of Bute | Two | Fixed, the one above the other | 13 & 16 | From NW. by W. to NE. by E. Southerly | 77 & 130 | 55° | 26′ | 5° | 7′ | 1790 |
| CORSEWALL | Western side of entrance to Loch Ryan, in Wigtonshire | One | Revolving, and shewing alternately a red and white light every 2 minutes | 15 | From NE. by E. to SW. Northerly | 112 | 55° | 1′ | 5° | 9′ | 1817 |
| LOCH RYAN | Cairn Ryan Point, within Loch Ryan, Wigtonshire | One | Fixed | 10 | From S. by W. ¹⁄₈ W. to N. ⁷⁄₈ E. Westerly | 30 | 54° | 58′ | 5° | 2′ | 1847 |
| MULL OF GALLOWAY | Southern extremity of the Mainland of Scotland, Wigtonshire | One | Intermittent, suddenly bursting into view, and continuing in sight 2¹⁄₂ min., then suddenly eclipsed for half a minute | 23 | From NE. to NW. ¹⁄₂ W. Southerly | 325 | 54° | 38′ | 4° | 51′ | 1830 |
| LITTLE ROSS | Little Ross Island, Kirkcudbrightshire | One | Flashing once every 5 seconds | 18 | From N. by E. to NW. by W. Southerly | 175 | 54° | 46′ | 4° | 5′ | 1843 |
| POINT OF AYRE | Northern extremity of Isle of Man | One | Revolving, and shewing alternately a red and white light every 2 minutes | 15 | From S. by W. to W. by N. Northerly | 106 | 54° | 25′ | 4° | 22′ | 1818 |
| CALF OF MAN | West side Calf Island, at the southern extremity of Isle of Man | Two | Revolving, and shewing white lights every 2 minutes | 22 & 24 | From NE. ¹⁄₃ to SW. W. Southerly | 275 & 368 | 54° | 3′ | 4° | 49′ | 1818 |
[89] At Hynish Point in Tyree Island, two fixed Lights are shewn from the Pier, but ONLY when the Vessel which attends the Lighthouse is expected to enter the Dock at Hynish. In the Trinity House Chart, Skerryvore Light is erroneously described as “Intermittent.”
[398]
BEACONS AND BUOYS.
FRITH OF FORTH DISTRICT.
| Name of Station. |
Description of Mark. |
Depth at Low Water of Spring Tides. |
Bearings of Marks and of Lines of Intersection Meeting at the Station. |
|---|---|---|---|
| MIDDLE BANK, WEST END, BUOY. | 6 Feet Buoy, Red. | 3¹⁄₂ Feet. | Alloa Tower in line with the Centre of Clackmannan Pier—Bearing N. by E. |
| Clackmannan Church Spire in line with High Chimney-Stack of Park-Farm House—Bearing NE. ¹⁄₂ E. | |||
| Middle Bank Buoy, East End—Bearing SE. by S. | |||
| MIDDLE BANK, EAST END, BUOY. | 6 Feet Buoy, Red. | 4 Feet. | Tullyallan House in line with Tullyallan Old Church Spire, in ruins—Bearing ESE. ¹⁄₂ S. |
| Remarkable Clump of Trees on distant high land in line with Airth Church Spire—Bearing W. by N. ¹⁄₂ N. | |||
| Buoy off Inch Brake Rock—Bearing S. by E. | |||
| INCH BRAKE BUOY. | 6 Feet Buoy, Black. | 5 Feet. | Flagstaff on the Ferry Pier, Kincardine, clear outside of Kincardine Stone Pier—Bearing N. by E. |
| Alloa Church Spire in line with South Corner of Kennet Pans Distillery Garden Wall—Bearing N. by W. | |||
| Long Annat Buoy—Bearing SSE. ¹⁄₂ E. | |||
| LONG ANNAT | 6 Feet Buoy, | 9 Feet. | Sands House, West Wing, in line with West Face of Annat Quarry—Bearing NNE. ¹⁄₂ E. |
| Binns Monument in line with the Middle of Bo’ness Pier—Bearing SE. by S. | |||
| Hen and Chicken’s Buoy—Bearing SE. by E. ¹⁄₄ S. | |||
| HEN AND CHICKEN’S BUOY. | 6 Feet Buoy, Black. | 12 Feet. | The East Wing of Culross Abbey in line with Eastmost House in Culross Village—Bearing NNE. ¹⁄₂ E. |
| Airth Castle, in line with High-Water Mark on Long Annat Point—Bearing NW. ¹⁄₄ W. | |||
| Buoy on East End of Dods’ Bank—Bearing SSE. ¹⁄₂ E. | |||
| DODS’ BANK BUOY.[399] | 7 Feet Buoy, Red. | 15 Feet. | Berry-Law Trees in line with the Chimney-Stack of Bunyan’s Farm—Bearing E. by N. |
| Chimney Stack of the Snub Coal Pit (the first Stack West of Kinneil New Iron Works), in line with the West Pier Wall of Bo’ness—Bearing WSW. ³⁄₄ W. | |||
| Comary House, East Wing, in line with the West Wing of the Factor’s House—Bearing N. by E. ³⁄₄ E. | |||
| Valleyfield House, a little East of the Eastern House on Preston Island, about half-way between the house and where the Island dries at half-tide—Bearing N. by E. ¹⁄₄ E. | |||
| The Buoy of Hen and Chicken’s Rock—Bearing NNW. ¹⁄₂ W. | |||
| BEAMER BEACON. | Painted Black, with Spherical Ball at top. | Rock Dry at Low Water. | Bo’ness Pier—Bearing NW. by W. |
| Charleston Pier, Outer End—Bearing NW. by N. | |||
| South-West Extremity of the Point at North Queensferry—Bearing ESE. ¹⁄₄ E. | |||
| The Halls, or principal South Queensferry Pier—Bearing SSE. ¹⁄₄ E. | |||
| DRUM SAND EAST BUOY. | 7 Feet Buoy, Red. | 12 Feet. | Newbigging House in line with East Edge of Carcraig Rock—Bearing NE. ¹⁄₂ E. |
| Oxscare Beacon—Bearing E. ³⁄₄ N. | |||
| Inchkeith Lighthouse—Bearing ESE. ¹⁄₂ E. | |||
| Highest Point of Arthur’s Seat in line with Nelson’s Monument—Bearing S. by E. ³⁄₄ E. | |||
| DRUM SAND WEST BUOY. | 8 Feet Buoy, Red, with Fenders. | 3¹⁄₄ Fathoms. | South Point of Inchkeith in line with Centre of Opening of Mickery Stone—Bearing ESE. ¹⁄₄ E. |
| Inchkeith Lighthouse—Bearing ESE. ¹⁄₂ E. | |||
| Fordel House in line with Centre of Donibristle House—Bearing N. ¹⁄₄ E. | |||
| Chimney-Stack of Castle Landhill Farm-House in line with End of Lazarett Pier—Bearing NW. ³⁄₈ N. | |||
| OXSCARE BEACON. | Painted Red, with Flat Cone at top. | Rock Dry at Low Water. | South Point of Carlin’s Nose—Bearing W. ³⁄₄ N. |
| Burntisland Pier—Bearing ENE. | |||
| Extremity of Kinghornness—Bearing E. ¹⁄₂ N. | |||
| Inchkeith Lighthouse—Bearing ESE. ¹⁄₄ E. | |||
| Martello Tower—Bearing SSE. ³⁄₄ E. | |||
| Granton Pier—Bearing S. by E. ¹⁄₄ E. | |||
| WEST GUNNET BUOY.[400] | 8 Feet Buoy, White. | 3³⁄₄ Fathoms. | Nelson’s Monument just clear East of North Leith Church Spire—Bearing SSW. |
| North Berwick Law in line with North End of Long Craig—Bearing ESE. ¹⁄₄ E. | |||
| Clump of Trees East of Grange House in line with Burntisland Church Spire—Bearing N. ¹⁄₂ W. | |||
| Inchkeith Lighthouse—Bearing E. ¹⁄₂ S. | |||
| EAST GUNNET BUOY. | 8 Feet Buoy, White. | 3¹⁄₂ Fathoms. | Notch at the foot of East Brow of the Pentland Hills in line with North Leith Church Spire—Bearing SSW. ³⁄₄ W. |
| Carlin’s Nose clear of the North Side of Mickery Stone—Bearing WNW. ³⁄₄ W. | |||
| Kinghorn New Free Church in line with Kinghornness—Bearing NE. by N. | |||
| Inchkeith Lighthouse—Bearing E. | |||
| PALLAS BUOY. | 7 Feet Buoy, Striped White and Black horizontally. | 3¹⁄₂ Fathoms. | Kinghorn Free Church in line with Swan’s Factory—Bearing N. by E. ³⁄₄ E. |
| North Brow of Inchkeith in line with the Centre of Silly Carr Rock—Bearing ENE. ¹⁄₄ N. | |||
| Assembly Hall Spire, Edinburgh, in line with Martello Tower—Bearing SW. ³⁄₄ S. | |||
| Inchkeith Lighthouse—Bearing ENE. ³⁄₄ E. | |||
| HERWIT BUOY. | 8 Feet Buoy, Black. | 4³⁄₄ Fathoms. | East Brow of Pentland Hills, touching West Brow of Arthur’s Seat (half way up)—Bearing SW. ¹⁄₂ W. |
| East Stables (Red-tiled House) of Pettycur in line with East Brow of Inchkeith—Bearing N. by W. | |||
| Inchkeith Lighthouse—Bearing N. by W. ¹⁄₂ W. | |||
| CRAIG WAUGH | 8 Feet Buoy, | 4 Fathoms. | Pettycur Pier in line with Eastern Brow of Inchkeith—Bearing N. by W. ¹⁄₂ W. |
| Assembly Hall Spire just clear, West of Nelson’s Monument—Bearing W. ³⁄₄ S. | |||
| Inchkeith Lighthouse—Bearing N. by W. ³⁄₄ W. | |||
| NORTH CRAIG MAST BUOY. | 12 Feet Mast Buoy, Chequered Red and White. | 3¹⁄₄ Fathoms. | Nelson’s Monument in line with West Wing of Leith Baths—Bearing WSW. ¹⁄₄ W. |
| Summit of East Lomond Hill in line with Big House Trees—Bearing N. ¹⁄₂ E. | |||
| Carlin’s Nose in line with Centre of Mickery Stone—Bearing WNW. | |||
| WEST ROCK-HEAD, OFF DYSART, BUOY.[401] | 6 Feet Buoy, Red. | 3¹⁄₄ Fathoms. | Dysart Coal-Pit Chimney-Stack in line with Middle of Gable of Pan Hall House—Bearing N. ¹⁄₄ E. |
| North End of Portbrae Church, Kirkcaldy, just clear of the End of Kirkcaldy Pier—Bearing WNW. ³⁄₄ W. | |||
| Inchkeith Lighthouse—Bearing SW. by S. | |||
| N.B.—The highest part of the Rock bearing N. ¹⁄₄ E. distant about one-half cable’s length from Buoy. | |||
| EAST ROCK-HEAD, OFF DYSART, BUOY. | 6 Feet Buoy, Black. | 3¹⁄₂ Fathoms. | Wemyss Old Castle in line with Southern Houses of East Wemyss—Bearing NE. by E. ¹⁄₄ E. |
| East Wing of Dysart Church in line with Town-House Steeple—Bearing NNW. ³⁄₄ W. | |||
| Buoy on West Rock-Head—Bearing W. by N. ¹⁄₄ N. | |||
| Inchkeith Lighthouse—Bearing SW. ¹⁄₂ S. | |||
| N.B.—The highest part of Rock, bearing NW. ¹⁄₄ W., distant about two cables’ lengths. | |||
| EAST VOWS ROCK, BEACON, OFF ELIE. | Pyramid of Iron Pillars, with open Cylindric Cage on top, painted Red. | Rock Dry at Low Water. | Ruins on Chapelness—Bearing N. ³⁄₄ E. |
| North End of Elie Pier—Bearing E. ³⁄₄ N. | |||
| Extremity of Elieness—Bearing E. by S. ¹⁄₂ S. | |||
| Isle of May Lighthouse—Bearing ESE. ¹⁄₄ S. | |||
| West Vows Rock—Bearing WNW. ¹⁄₂ N. distant ¹⁄₂ mile. | |||
| Buoy on Thill Rock—Bearing ESE. ¹⁄₈ S. distant two cables’ lengths. | |||
| THILL ROCK BUOY. | 7 Feet Buoy, Black. | 3³⁄₄ Fathoms. | West End of Millhouse Cottage in line with North End of Elie Pier—Bearing NE. |
| Pettie Law in line with West Chimney-Stack of David Ovenstone’s House—Bearing N. ³⁄₈ W. | |||
| Ruin on Chapelness—Bearing NNW. ¹⁄₂ W. | |||
| Beacon on East Vows Rock—Bearing WNW. ¹⁄₈ N. | |||
| N.B.—The Buoy lies about 35 fathoms to the SSE. of the highest part of the Rock. | |||
| SOUTH CARR BEACON. | Painted Red, with Cross at top. | Rock Dry at Low Water. | Cairn on Bass Rock—Bearing N. by E. |
| Isle of May Lighthouse—Bearing NE. | |||
| Dunbar Church Tower—Bearing SSE. ¹⁄₄ S. | |||
| Oldham Farm-House Chimney-Stack—Bearing W. ¹⁄₄ N. | |||
| NORTH CARR BEACON. | Beacon of Stone, with Iron Frame and Ball. | Rock Dry at Low Water. | 1¹⁄₄ Mile from Fifeness—Bearing from Isle of May Light NNE. distant 6 Nautic Miles. |
[402]
BEACONS AND BUOYS.
DISTRICT OF FRITHS OF MORAY, CROMARTY, INVERNESS,
AND DORNOCH.
| Name of Station. |
Description of Mark. |
Depth at Low Water of Spring Tides. |
Magnetic Bearings of Marks and of Lines of Intersection Meeting at the Station. |
|---|---|---|---|
| COVESEA SKERRIES BEACON. | Pyramid of Iron Pillars, with open cylindric Cage, and a Cross, rising to the height of about 50 feet above High water. | Rock dry at Low water. | Covesea Skerries Lighthouse on the neighbouring land of Craighead—Bears WSW. ¹⁄₄ W. distant one mile. |
| LONGMAN POINT BEACON. | Cone of Iron Plates painted Black. | Beach Dry at Low water of Spring Tides. | End of Kessock South Pier—Bearing W. by N. ¹⁄₄ N. |
| Craigtown Point—Bearing NW. ¹⁄₂ W. | |||
| Meiklemee, East End Buoy—Bearing E. ¹⁄₂ N. | |||
| Bogbain House in line with Rigmore House—Bearing S. ³⁄₄ E. | |||
| End of Longman Point—Bearing N. ¹⁄₄ W. distant 40 Fathoms. | |||
| MEIKLEMEE BANK BUOY. East End. |
6 Feet Buoy. Black. |
12 Feet. | Park’s Farm-House in line with Rigmore House—Bearing SSW. |
| Middle of space between the Houses of Scorguoy Farm-Yard in line with Black Mill Chimney—Bearing W. ¹⁄₄ S. | |||
| Chanonry Point Lighthouse—Bearing ENE. ¹⁄₄ E. | |||
| MIDDLE BANK BUOY. East End. |
6 Feet Buoy. Black. |
12 Feet. | Scorguoy Farm-Yard (South End), in line with Black Mill Chimney—Bearing W. ¹⁄₂ S. |
| Round Clump of Trees, North of Ley’s House, in line with Rigmore House—Bearing SW. ³⁄₄ S. | |||
| Chanonry Point Lighthouse—Bearing ENE. | |||
| Meiklemee Bank Buoy—Bearing W. ⁵⁄₈ S. | |||
| PETTY BANK BUOY. North or Outer Edge. |
6 Feet Buoy. Chequered Black and White. | 12 Feet. | Dalcross Castle in line with Fishtown Farm-House—Bearing SE. ³⁄₄ S. |
| Extremity of East Suter in line with Store-house, Chanonry Point—Bearing ENE. ³⁄₄ N. | |||
| Munlochy Buoy—Bearing N. | |||
| MUNLOCHY BUOY.[403] | 6 Feet Buoy. Black. |
12 Feet. | West Wing of Avoch House, now in ruins, in line with the most Western slated House or Cottage in Avoch—Bearing N. ¹⁄₄ W. |
| North End of Fort-George in line with Chanonry Point—Bearing ENE. ¹⁄₄ E. | |||
| SKATE BANK BUOY. East End. |
6 Feet Buoy. Black. |
12¹⁄₂ Feet. | The East Wing of Kincurdie House in line with Spire of Rosemarkie Kirk—Bearing NNE. ¹⁄₂ E. |
| Flagstaff of Fort-George in line with the Outer End of Chanonry Pier—Bearing ENE. ¹⁄₄ E. | |||
| Dalcross Castle in line with Cottage on Sea-cliff—Bearing S. ³⁄₄ E. | |||
| Munlochy Buoy—Bearing WSW. ¹⁄₈ W. | |||
| CRAIGMEE OR FORT-GEORGE BANK BUOY. | 6 Feet Buoy. Chequered Black and White. |
2¹⁄₄ Fathoms. | High Part, or West Brow of Altarlie Point, in line with Chanonry Point Lighthouse—Bearing SW. ³⁄₄ W. |
| Patch of Trees at West End of Broomhill Wood, called Broomhill Bush, in line with Platcock House—Bearing WNW. ¹⁄₄ W. | |||
| RIFF BANK BUOY. West End. |
6 Feet Buoy. Black. |
3²⁄₃ Fathoms. | Craighead Farm-House in line with the most Western of the Three Burns—Bearing N. by E. ¹⁄₄ E. |
| Broomhill Bush (East End) in line with the Manse of Rosemarkie—Bearing W. ¹⁄₂ N. | |||
| Chanonry Point Lighthouse—Bearing WSW. ³⁄₄ S. | |||
| RIFF BANK BUOY. Middle or North Angle. |
6 Feet Buoy. Black. |
3¹⁄₂ Fathoms. | Three remarkable Trees at North End of Craigie Wood, in line with Rosemarkie Manse—Bearing W. ¹⁄₂ S. |
| Gamekeeper’s House at End of Wood in line with Cave on Sea-shore, a little East of the Three Burns—Bearing NW. ¹⁄₂ W. | |||
| Chanonry Point Lighthouse—Bearing WSW. ¹⁄₂ S. | |||
| RIFF BANK BUOY. East End. |
12 Feet Mast-Buoy. Black. |
4¹⁄₂ Fathoms. | Castle Craig Rock in line with Stack Rock at foot of West Suter—Bearing N. by E. ¹⁄₄ E. |
| Store-House on Chanonry Point, shut in by the North corner of Fort-George, and in line with Lower part of South Brow of Ord Hill—Bearing W. ³⁄₄ S. | |||
| Towrie Lumb Wood in line with Craigie Wood (South End)—Bearing W. | |||
| WHITENNESS BEACON. (In preparation.)[404] |
— | — | — |
| NAVITY BANK BUOY. South Edge. |
6 Feet Buoy. Chequered Black and White. |
2¹⁄₂ Fathoms. | Trees at end of Navity Farm-House in line with East Bank or Cliff of Craighouse Burn—Bearing N. ³⁄₄ E. |
| Extremity of Wood on Brow of East Suter in line with Lower part of Brow of West Suter—Bearing NE. by E. | |||
| Chanonry Point Lighthouse—Bearing SW. by W. | |||
| Riff Bank Mast Buoy—Bearing SE. ⁵⁄₈ E. | |||
| NIGG SANDS BUOY. East End. |
6 Feet Buoy. Black. |
2 Fathoms. | Cromarty Gaelic Kirk Steeple in line with East Wing of Hotel—Bearing S. ³⁄₄ E. |
| Face of East Suter apparently on a line halfway between Ferryhouse and Stable—Bearing SE. by E. | |||
| NIGG SANDS BUOY. West End. |
6 Feet Buoy. Black. |
1²⁄₃ Fathoms. | Farm-House of Dalney in line with the Pigeon-house East of Ballintrade—Bearing NNE. ¹⁄₈ E. |
| Extremity of West Suter in line with Cromarty Lighthouse—Bearing SE. ⁵⁄₈ E. | |||
| NEWHALL BANK BUOY. East End. |
6 Feet Buoy. Chequered Black and White. |
2¹⁄₂ Fathoms. | Priesthill Farm-House in line with Easternmost House in Ballintrade—Bearing NNE. ³⁄₄ E. |
| East Brow of West Suter in line with Cromarty Gaelic Kirk—Bearing ESE. ¹⁄₈ S. | |||
| Nigg Sands West Buoy—Bearing ENE. ³⁄₈ N. | |||
| THREE KINGS ROCKS BUOY. | 8 Feet Buoy. Red. |
7¹⁄₂ Fathoms. | Eastern Trees upon Top of the High Land, being the most projecting and highest part of Sea Cliff, West of Gilliam Burn, in line with the Highest Eastern part of Three Kings Rock—Bearing WNW. ¹⁄₄ N. |
| Duke of Sutherland’s Monument in line with West End of Long Storehouse in Shandwick—Bearing N. by E. ³⁄₈ E. | |||
| CULLODEN ROCK BUOY. | 8 Feet Buoy. Black. |
8³⁄₄ Fathoms. | Brucefield Farm-House in line with Tarbetness Lighthouse Flag-Staff—Bearing WSW. ³⁄₄ W. |
| Duke of Sutherland’s Monument in line with Lower Corner of Wood farthest West from Dunrobin Castle—Bearing NNW. | |||
| FAIRWAY BUOY OFF TAIN BAR.[405] |
12 Feet Mast Buoy. Red. |
5 Fathoms. | West End of Bentavie Hill in line with Trentham Farm-House—Bearing NNW. ⁷⁄₈ W. |
| West Brow of East Suter in line with Meiklerennie Farm-House—Bearing SW. ³⁄₈ W. | |||
| Tarbetness Lighthouse—Bearing SE. ³⁄₄ E. | |||
| TAIN BAR INNER BUOY. North Side. |
6 Feet Buoy. Black. |
2¹⁄₂ Fathoms. | Remarkable Hollow or Notch in High Land East of East Suter, in line with Lochslain Castle—Bearing SSW. ¹⁄₄ W. |
| Lower West Brow of Cambusmore Hill in line with East End of West Embo Wood—Bearing N. by W. ³⁄₄ W. | |||
| Tarbetness Lighthouse—Bearing ESE. ¹⁄₂ S. | |||
| Fairway Buoy off Tain Bar—Bearing E. ³⁄₄ S. | |||
| TAIN BAR INNER BUOY. South Side. |
6 Feet Buoy. Chequered Black and White. |
4²⁄₃ Fathoms. | Remarkable Hollow or Notch in High Land East of East Suter in line with Meiklerennie Farmhouse—Bearing SSW. ³⁄₈ W. |
| West End of East Embo Wood in line with Embo Farmhouse—Bearing N. ¹⁄₂ W. | |||
| Fairway Buoy off Tain Bar—Bearing E. ¹⁄₄ N. | |||
| Tain Bar Inner Buoy (North Side)—Bearing ENE. ³⁄₈ N. | |||
| Dornoch Spire—Bearing NNW. ³⁄₄ W. |
[406]
BEACONS AND BUOYS.
FRITH OF CLYDE DISTRICT.
| Name of Station. |
Description of Mark. |
Depth at Low Water of Spring Tides. |
Bearings of Marks and of Lines of Intersection Meeting at the Station. |
|---|---|---|---|
| FULLARTON ROCK BUOY. | 7 Feet Buoy. Red. |
3¹⁄₂ Fathoms. | Clump of Trees at East side of Clachlan Farm, just opening from the West Brow of Holy Island—Bearing N. by E. |
| Standing Stone upon Kinross Point—Bearing W. | |||
| Buoy moored upon ESE. Tail of Rock. The shallowest part of Rock has 8 Feet at Low water of Spring Tides. | |||
| ARRANMAN’S BARRELS ROCKS BUOY. | 8 Feet Buoy. Red. |
8¹⁄₂ Fathoms. | West End of Arranman’s Barrels Shoal—Bearing W. by N. |
| North-East Extremity of Shoal—Bearing N. ¹⁄₂ E. | |||
| Ballyshare House in line with the Lower East End of Dunacreein Rock—Bearing NW. ¹⁄₂ W. | |||
| The Buoy is moored abreast of the middle of the Shoal, and is distant from the Low water Rocks about half a cable’s length. | |||
| OTTERARD ROCK BUOY. | 8 Feet Buoy. Black. |
3³⁄₄ Fathoms. | Clump of Trees at Ballaminich Farm-House in line with the lower part of the South-eastern Brow of Island Davaar—Bearing SW. ¹⁄₄ W. |
| The remarkable Notch in distant Hill called Balavilan, in line with North End of Green Patch on the rising ground in Field south of Long Dyke near Smerby Farm-House—Bearing WNW. ³⁄₄ N. | |||
| Macrinnan’s Point—Bearing WSW. ¹⁄₂ W. | |||
| The Buoy is moored upon ESE. Tail of Rock. The shallowest part of Rock at Low water of Springs has 12 Feet. | |||
| MILLBEG BANK BUOY. | 6 Feet Buoy. Black. |
2 Fathoms. | Campbelton Town-House Spire in line with House in ruins on Trench Point—Bearing WNW. |
| Crossbeg Farm-House in line with Lower part or Mouth of Porter’s Glen—Bearing N. ¹⁄₄ W. | |||
| CAMPBELTON HARBOUR OUTER BUOY.[407] | 6 Feet Buoy. Red. |
2¹⁄₄ Fathoms. | West Corner of Gaelic Church in line with Trench Point—Bearing W. by N. ¹⁄₄ N. |
| West End of Baraskie Farm-House (dwelling-house) in line with Angle of Plantation, and also with the Corner of the Second Field to the South of the House—Bearing N. ³⁄₈ E. | |||
| CAMPBELTON HARBOUR INNER BUOY. | 6 Feet Buoy. Black. |
1¹⁄₄ Fathoms. | Castle Hill Church in line with high water-mark on Trench Point—Bearing WNW. ¹⁄₄ W. |
| North End of Higher Glenremisdil Farm-House in line with Cottage at East End of Hetly House—Bearing SW. ³⁄₄ S. | |||
| MILLMORE BEACON. | Pyramid of Iron Spars with Wire Ball on top. | Beach dry at Low water. | Campbelton North Pier-head—Bearing NW. by W. |
| Macrinnan’s Point—Bearing ENE. ¹⁄₄ N. | |||
| TRENCH POINT BEACON. | Pyramid of Iron Spars with Wire Ball on top. | Beach dry at Low water. | Campbelton North Pier-head—Bearing NW. by W. |
| Outer or Red Buoy (above described)—Bearing ESE. ¹⁄₄ E. | |||
| LAPPOCK BEACON. | Tower with Stone Ball on top, painted Red. | Rock dry at Low water. | Troon Harbour Light—Bearing S. by W. ¹⁄₄ W. |
| Beacon on Lady Isle—Bearing SW. ¹⁄₂ W. | |||
| Extremity of Ardrossan Pier—Bearing NNW. ¹⁄₄ W. | |||
| BREAST ROCK BEACON. | Pyramid of Iron Pillars, with cylindric open Cage, painted Red. | Rock dry at Low water. | Turnberry Point—Bearing NE. by N. ¹⁄₈ E. |
| Pladda Lighthouse—Bearing NNW. | |||
| Ailsa Craig (Highest Point)—Bearing W. | |||
| LOCH RYAN INNER BUOY. | 7 Feet Buoy. Red. |
3¹⁄₂ Fathoms. | Mr Moore’s Pigeon-House in line with Angle of Plantation lying to the North of Corsewall House—Bearing N. by W. ³⁄₈ W. |
| East End of Cairn Ryan Hill Quarry, and East End of Plantation, at the foot of the same hill, in line with North Chimney of Mrs Begg’s Inn, Cairn Ryan Village—Bearing NE. ³⁄₄ N. | |||
| North End of Stranraer Pier—Bearing SSW. ¹⁄₄ W. | |||
| BEACON ON THE SPIT OF SCAR POINT, OFF KIRKCOLM POINT, IN LOCH RYAN. | Cone of Iron Plates, painted Red. | Dry at Low water. | Loch Ryan Lighthouse—Bearing NNE. ¹⁄₄ E. |
| Lochnoll Houses—Bearing SE. by E. | |||
| Stranraer Pier End—Bearing SSW. ¹⁄₂ W. | |||
| Waukmill Houses—Bearing SW. by W. | |||
| Corsewall House in line with The Scar off Kirkcolm Point—Bearing NNW. ¹⁄₄ N. | |||
| LOCH RYAN OUTER BUOY.[408] | 7 Feet Buoy, Black. |
3¹⁄₂ Fathoms. | Portincally Farm-House in line with the Brow of Clachan Head—Bearing NNW. ¹⁄₄ W. |
| Mr Charles M‘Donald’s House in line with the South End of General Wallace’s Porter’s Lodge—Bearing SE. | |||
| LAGGAN, OR EBBSTONE ROCK BEACON. | Pyramid of Iron Pillars, with cylindric Open Cage on top, painted Red. | Rock dry at Low water. | Corsewall Lighthouse—Bearing NE. by E. |
| Ailsa Craig (Highest Point)—Bearing NE. ³⁄₄ N. | |||
| Laggan Point—Bearing SSE. ¹⁄₂ E. |
BEACONS AND BUOYS.
LOCH FYNE DISTRICT.
| Name of Station. |
Description of Mark. |
Depth at Low Water of Spring Tides. |
Magnetic Bearings of Marks and of Lines of Intersection Meeting at the Station. |
|---|---|---|---|
| OFF ARDLAMONT POINT OR BRADEICH ROCKS, ARGYLESHIRE, BUOY. | 8 Feet Buoy. Red. |
2³⁄₄ Fathoms. | South-West Extremity of West and Eastern Hills upon Ardlamont Point in line with Extremity of Point—Bearing NW. ³⁄₄ W. |
| Highest Part of Bradeich Rocks—Bearing NNW. ¹⁄₂ W. | |||
| South End of Inchmarnock Island—Bearing S. ¹⁄₂ W. | |||
| Extremity of Land South of Ardlamont Point—Bearing N. by W. | |||
| The Buoy lies about 115 fathoms distant from High water-mark upon the Point, and about 45 fathoms from the highest part of Bradeich Rocks. | |||
| N.B.—There is a small Rock which dries at Low Spring Tides, about 10 or 12 fathoms outside of the highest main Rock. | |||
| SKERNA SCALLAIG ROCK, OFF ENTRANCE TO CRINAN CANAL, ARGYLESHIRE, BUOY. | 7 Feet Buoy. Red. |
2¹⁄₂ Fathoms. | South Wing of Sir John Ord’s Stables in line with North Extremity of Dunchoan Island—Bearing NE. by E. |
| Silver Craig’s Point, Island More—Bearing SE. by S. ¹⁄₂ E. | |||
| West Wing of Ardrishaig Hotel in line with Lighthouse upon End of Ardrishaig Pier—Bearing N. ¹⁄₂ E. | |||
| N.B.—The Buoy lies upon the South-West tail of the Shoal or Rock. | |||
| OTTER BANK BEACON, OFF ENTRANCE TO LOCH FYNE,
ARGYLLSHIRE. (Building.)[409] |
Conical Iron Beacon. To be painted Black. |
Gravel Beach. Dry at Low water. |
Auchabolonabaith House (East Wing) in line with Centre of Cottage—Bearing N. by W. ¹⁄₄ W. |
| Strathlachlan Hill in line with Schoolhouse Point—Bearing ENE. | |||
| End of Liath Island—Bearing W. ¹⁄₄ S. | |||
| WEST OTTER BEACON, OFF CASTLE LACHLAN, LOCH FYNE, ARGYLESHIRE. (Building.) |
Conical Iron Beacon. To be painted Black. |
Gravel Beach. Dry at Low water. |
End of Minard Point—Bearing SW. by W. ¹⁄₄ W. |
| End of Chapel Island—Bearing ENE. ³⁄₄ E. | |||
| Barneycarry Farmhouse in line with North-East End of Hugh Island—Bearing SE. ¹⁄₄ E. |
BEACONS AND BUOYS.
OBAN BAY, ARGYLESHIRE.
| Name of Station. |
Description of Mark. |
Depth at Low Water of Spring Tides. |
Magnetic Bearings of Marks and of Lines of Intersection Meeting at the Station. |
|---|---|---|---|
| SKERRAT ROCK. S. W. End. |
10 Feet Buoy, with Fenders. Red. |
Dry at Low-water of Spring Tides. | Centre of Oban Free Church Window in line with North-Eastern Chimney of Freemason’s Hall—Bearing SE. by E. |
| Centre of Skerry Dhu or Black Rock (apparently in middle of Sound of Kerrera) in line with Ardincaple Point—Bearing WSW. | |||
| Buoy on North-Eastern End of Skerrat Shoal—Bearing NE. ¹⁄₂ E. distant 105 fathoms. | |||
| SKERRAT SHOAL, N. E. End. |
6 Feet Buoy. Chequered Black and White. |
12 Feet at Low water of Spring Tides. | Oban Free Church Steeple in line with South Chimney Top of Spring Well Cottage—Bearing SE. |
| Ardincaple Point, a little West of the Western End of Skerry Dhu or Black Rock—Bearing WSW. | |||
| Buoy on Skerrat Rock—Bearing SW. ¹⁄₂ W. distant 105 fathoms. | |||
| N.B.—No Vessel should attempt to pass between those Buoys. | |||
[410]
BEACONS AND BUOYS.
LINNHE LOCH DISTRICT, ARGYLESHIRE.
| Name of Station. |
Description of Mark. |
Depth at Low Water of Spring Tides. |
Magnetic Bearings of Marks and of Lines of Intersection Meeting at the Station. |
|---|---|---|---|
| CULCHENNA SPIT BUOY. | 10 Feet Mast Buoy, with Red Ball. | 4 Fathoms. | West End of Ardgour House in line with East End of Hugh Boyd’s Cottage—Bearing N. ⁷⁄₈ E. |
| John Cameron’s Cottage in line with End of Culchenna Point—Bearing NE. ³⁄₄ E. | |||
| Sallachan Point—Bearing NNW. ¹⁄₄ W. | |||
| Chlavoulin Spit Buoy—Bearing N. ³⁄₄ E. | |||
| CHLAVOULIN SPIT BUOY. | 7 Feet Buoy. Black. |
2 Fathoms. | Centre of Ardgour House in line with Centre of Hugh Boyd’s Cottage—Bearing N. by E. |
| East End of Second Wood from Corran Point in line with Barn at East End of Hugh Campbell’s Cottage (Eastern House in Village of Chlavoulin)—Bearing NE. ³⁄₄ E. | |||
| Corran Flat Buoy—Bearing ENE. ³⁄₄ E. | |||
| End of Sallachan Point—Bearing W. | |||
| CORRAN FLAT BUOY. | 6 Feet Buoy. Black. |
3³⁄₄ Fathoms. | West End of Brow of Sallachan Hill covered with Wood in line with Donald M‘Lean’s House—Bearing NW. by W. ¹⁄₄ W. |
| West Chimney-Stack of South Corran Ferry House in line with White Part of Rock near High Water Mark at the End of a Dyke—Bearing E. ³⁄₄ N. | |||
| South Brow of Stroncrigan Hill in line with End of Corran Cliff—Bearing NE. by E. ¹⁄₈ E. | |||
| CORRAN BANK, NORTH-WEST END, BUOY. | 6 Feet Buoy. Chequered Black and White. |
2³⁄₄ Fathoms. | Bunrie Point in line with High Water Mark on Corran Point—Bearing S. by W. ¹⁄₂ W. |
| Belfry of Corran Church—Bearing W. by N. | |||
| CORRAN BANK, SOUTH-EAST END, BUOY.[411] | 6 Feet Buoy. Black. |
3¹⁄₂ Fathoms. | Culchenna Point and Kintallon Point, in line with End of Cliff of Corran Point—Bearing SW. by S. ¹⁄₈ W. |
| Belfry of Corran Church—Bearing NW. by W. ⁵⁄₈ W. | |||
| South Keil Farmhouse, in line with Arch of Bridge on Road—Bearing NNW. | |||
| Corran Bank North Buoy—Bearing NNW. | |||
| LOCHYFLAT EAST BUOY. | 6 Feet Buoy. Red. |
2³⁄₄ Fathoms. | South End of Wood at Stroncrigan Point, just clear of Cambusnagaul Point—Bearing SW. by W. ³⁄₄ W. |
| East End of Donald Cameron’s House in Corpach, in line with North End of Old Engine House—Bearing N. by W. ¹⁄₄ W. | |||
| South End of Free Church in line with North End of Greyhouse, or Old Corpach House—Bearing N. ⁷⁄₈ E. | |||
| Entrance of Caledonian Canal—Bearing N. by W. ¹⁄₂ W. | |||
| LOCHYFLAT MIDDLE BUOY. | 6 Feet Buoy. Red. |
3¹⁄₂ Fathoms. | East End of Henderson’s House or Croft in line with East End of Schoolhouse near Cambusnagaul Point—Bearing W. ¹⁄₂ S. |
| Fish-house in line with End of Dearg Point—Bearing N. by W. ³⁄₄ W. | |||
| Entrance of Caledonian Canal—Bearing N. | |||
| North End of Wood at Banavie at South Side of Canal in line with Clump of Trees at East End of John Cameron’s Cottage in Kilcorpach—Bearing NE. by E. ¹⁄₄ E. | |||
| Buoy on East End of Lochyflat—Bearing NE. ³⁄₄ N. | |||
| M‘Lean’s Rock Buoy—Bearing NW. by N. | |||
| LOCHYFLAT WEST BUOY. | 6 Feet Buoy. Red. |
3 Fathoms. | Cameron’s Monument in line with End of Dearg Point—Bearing N. ¹⁄₄ E. |
| North or Steep Face of Donnay Hill in line with South Wing of Old Castle of Inverlochy—Bearing E. ³⁄₈ S. | |||
| Lochyflat Middle Buoy—Bearing NE. | |||
| M‘Lean’s Rock Buoy—Bearing N. by E. ¹⁄₄ E. | |||
| Fort-William Pier—Bearing SSW. ¹⁄₈ W. | |||
| MACLEAN’S ROCK, LOCHEILHEAD, BUOY.[412] | 6 Feet Buoy. Black. |
3³⁄₄ Fathoms. | Old Engine-House in line with High Water Mark on South End of Island Creiah—Bearing N. by E. ¹⁄₈ E. |
| North Brow of Donnay Hill in line with Alan Kennedy’s Barn, Southmost House in Kilcorpach—Bearing E. ³⁄₄ S. | |||
| Lochyflat West Buoy—Bearing S. by W. ¹⁄₄ W. | |||
| Fort-William Pier—Bearing S. by W. ³⁄₄ W. | |||
| NEW ROCK, LOCHEILHEAD, BUOY. | 6 Feet Buoy. Chequered Black and White. |
3 Fathoms. | Cameron’s Monument in line with End of Dearg Point—Bearing N. ¹⁄₄ E. |
| North End of Free Church in line with High Water Mark on East End of Island Creiah—Bearing NE. ³⁄₄ N. | |||
| Centre of Donnay Hill in line with Alan Kennedy’s Barn—Bearing E. ⁷⁄₈ S. | |||
| N.B.—Depth at Low Water of Spring Tides on Rock is 8 feet. The Buoy, moored in 3 fathoms, swings clear of the Rock on west side of it. |
By order of the Board,
ALAN STEVENSON, Engineer.
Edinburgh, 1st January 1848.
NOTICE TO MARINERS.
The Commissioners of Northern Lighthouses have resolved to publish, on 1st January annually, for the use of Mariners, a Descriptive List of all the Lighthouses, Beacons, and Buoys under their charge, giving the characteristic appearance and correct bearings of each.
Mariners are particularly requested to notice, that they should NEVER PURCHASE any List EXCEPT THAT FOR THE YEAR CURRENT at the time of purchase. As changes may have taken place, no reliance can be placed on any List which has been published for a preceding year.
Publishers are particularly cautioned not to sell any List which has been published on a preceding year. Arrangements have been made with the Publishers of the Board, that all copies remaining on hand with any Publisher, at the close of any year, will be exchanged for the New Issue; and all Publishers are MOST PARTICULARLY REQUESTED not to retain on hand any copies of a past issue.
By Order of the Board,
ALEX. CUNINGHAM, Secretary.
Northern Lights Office,
Edinburgh, 1st January 1848.
}
[413]
The gross amount of Duties received from Shipping in the year to 31st December 1846, as per detailed State appended hereto (No. I., p. 429), is £46,001 : 11 : 2⁶⁄₈.
The Commission paid to Collectors in the same period is £2401 : 7 : 3⁴⁄₈, and Repayments of Duties erroneously charged, &c., £218 : 16 : 10²⁄₈, making the nett amount of Duties for the year £43,381 : 7 : 1, as also appears from State, No. I., p. 429.
| The nett amount of Duties in the year 1845 was | £52,391 | 8 | 4 | |||||
| While that received in 1846 is | 43,381 | 7 | 1 | |||||
| Making a Deficiency in the year of | £9,010 | 1 | 3 | |||||
| Whereof— | ||||||||
| Half-year to 30th June, | £2350 | 9 | 1 | |||||
| Ditto to 31st December, | 6659 | 12 | 2 | |||||
| £9,010 | 1 | 3 | ||||||
It is to be observed, however, that during the currency of this year, two reductions in the amount of Light-duties, resolved upon by the Board, have come into operation.
1. The first of these reductions was one halfpenny per ton (or one-half of the amount leviable by Statute) for the Bell Rock Light; one farthing per ton (or one-half of the amount leviable) for each of the Lights of Corsewell and Mull of Galloway; and one-eighth of a penny per ton (or one-fourth of the amount leviable) for Pladda Light. These reductions[414] were in operation during the first half of the year 1846. They were estimated to produce a deficiency in the annual Revenue of £5160, which, for the half-year, gives £2580. The actual deficiency in the amount levied for the first half of 1846, over that levied in the corresponding period of the preceding year, was £2350 : 9 : 1, being still £230 under the estimated amount.
2. The Board came to the resolution of making such a further reduction as should, including the previous one, give an aggregate abatement to the Coasting Trade, for each of the Lighthouses, of 50 per cent., that is, the amount leviable for each of the Lights being, previous to the first reduction, one halfpenny per ton, was reduced for the Coasting Trade to one farthing per ton; the amount for the Bell Rock and Skerryvore Lights, being one penny, was reduced to one halfpenny per ton. This reduction commenced on the 1st day of July 1846, and has consequently been in operation during the last half of that year. It was estimated to produce a deficiency in the annual revenue of the Board of £14,394 : 14 : 5, which, for the half-year, gives £7197 : 9 : 2. The actual deficiency in the amount levied for the last half of 1846, over that levied in the corresponding period of the preceding year, was £6659 : 12 : 2, being £540 under the estimated amount.
| It is also proper to observe, that while there is the above deficiency in Receipts of the year 1846, as contrasted with 1845, of | £9010 | 1 | 3 | |
| There was a surplus Receipt of the year 1845, as contrasted with 1844, amounting to | 6612 | 17 | 8 | |
| Making the Deficiency in 1846, as contrasted with the Receipts of 1844, upon which the calculations of the Board were founded, only | £2397 | 3 | 7 | |
On the other hand, the greater reduction having been in operation only during half the year, a greater deficiency in the Revenue must be looked for in future years.
The Light-Duties in 1845 were contributed by 163,174 vessels in the Coasting Trade, giving an aggregate tonnage of 15,566,461, and by 45,612 vessels in Oversea Trade, giving an aggregate tonnage of 9,300,983.
[415]
The Light-Duties in 1846 have been contributed by 163,166 vessels in the Coasting Trade, giving an aggregate tonnage of 15,926,634, and by 50,324 vessels in the Oversea Trade, giving an aggregate tonnage of 9,577,478.
A contrast of these statements shews an increase in the Coasting Trade of 1846 in tonnage of 360,173, with eight fewer vessels; and in the Oversea Trade an increase of 4712 vessels, with a tonnage of 276,495.
These results (somewhat singular in their relative amounts) establish the important fact, that, though there is a deficiency in the revenue of the Board, it truly arises from the reductions in the Duties, and not from any reduction in the Shipping.
For the information of the Board, there will be found appended (p. 433) a statement shewing the progressive increase of tonnage during the last four years.
| The amount of Duties received in the year 1846, as above, is | £46,001 | 11 | 2 | ⁶⁄₈ | ||||
| While the Ordinary Expenditure of the Board has been | 32,063 | 6 | 3 | |||||
| Giving a Surplus Receipt for the year to meet Extraordinary Expenditure of (see State, No. II., p. 432) | £13,938 | 4 | 11 | ⁶⁄₈ | ||||
| But the total Expenditure of the Board in the Year has been | £60,374 | 15 | 9 | ²⁄₈ | ||||
| From which if there be deducted the Gross Receipts, per page 425, | 47,895 | 8 | 8 | ⁶⁄₈ | ||||
| It gives a Balance superexpended beyond the surplus of the year of | £12,479 | 7 | 0 | ⁴⁄₈ | ||||
| The Balance on hand at 31st March 1846 was | £42,069 | 6 | 10 | |||||
| While that on hand at 31st March 1847 is | 29,589 | 19 | 9 | ⁴⁄₈ | ||||
| Difference equal to superexpenditure, | £12,479 | 7 | 0 | ⁴⁄₈ | ||||
[416]
There has been expended on the various Works in progress, prior to the year 1846 and in that year, as follows:—
| Prior to 1846. |
In 1846. | Total. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Skerryvore Lighthouse Works | £93,576 | 10 | 0 | £227 | 8 | 2 | £93,803 | 18 | 2 | |||
| Add Bo-Pheg Beacon | 416 | 10 | 7 | 25 | 10 | 1 | 442 | 0 | 8 | |||
| £93,993 | 0 | 7 | £252 | 18 | 3 | £94,245 | 18 | 10 | ||||
| Covesea Lighthouse Works | 9,523 | 17 | 6 | 1,109 | 5 | 4 | 10,633 | 2 | 10 | |||
| Cromarty Ditto | 2,895 | 18 | 8 | 342 | 9 | 3 | 3,238 | 7 | 11 | |||
| Chanonry Ditto | 2,832 | 16 | 1 | 405 | 7 | 8 | 3,238 | 3 | 9 | |||
| Ardnamurchan Ditto | 296 | 2 | 2 | 2,343 | 17 | 6 | 2,639 | 19 | 8 | |||
| Laggan Spur Beacon | ... | ... | 748 | 10 | 6 | 748 | 10 | 6 | ||||
| Island Glass New Buildings and Inclosures | 3,064 | 15 | 3 | 1,797 | 3 | 5 | ¹⁄₂ | 4,861 | 18 | 8 | ¹⁄₂ | |
| Nosshead Lighthouse Works | ... | ... | 1,467 | 6 | 1 | 1,467 | 6 | 1 | ||||
| Loch Ryan Ditto | ... | ... | 829 | 12 | 9 | ¹⁄₂ | 829 | 12 | 9 | ¹⁄₂ | ||
| Pentland Skerries New Works | ... | ... | 3,135 | 17 | 5 | ¹⁄₂ | 3,135 | 17 | 5 | ¹⁄₂ | ||
| Ditto Dioptric Light | ... | ... | 2,037 | 11 | 4 | 2,037 | 11 | 4 | ||||
| Renewal of Fixed Lights | ... | ... | 3,035 | 14 | 4 | 3,035 | 14 | 4 | ||||
| Buoys, &c. | ... | ... | 1,549 | 14 | 11 | ¹⁄₂ | 1,549 | 14 | 11 | ¹⁄₂ | ||
| Campbeltown Beacons | ... | ... | 17 | 4 | 10 | 17 | 4 | 10 | ||||
| Lappock Beacon | ... | ... | 8 | 12 | 5 | 8 | 12 | 5 | ||||
| Startpoint New Works | ... | ... | 5 | 19 | 4 | 5 | 19 | 4 | ||||
| Elie or Vows Beacon | ... | ... | 205 | 5 | 8 | 205 | 5 | 8 | ||||
| Whiteness Beacon | ... | ... | 152 | 5 | 8 | 152 | 5 | 8 | ||||
| Longman’s Point Ditto | ... | ... | 164 | 15 | 6 | 164 | 15 | 6 | ||||
| Loch Ryan Ditto | ... | ... | 152 | 5 | 9 | 152 | 5 | 9 | ||||
| Brist Beacon | 734 | 2 | 9 | 8 | 12 | 5 | 742 | 15 | 2 | |||
| Mull of Kintyre Dykes and Road | 586 | 14 | 4 | 647 | 17 | 9 | 1,234 | 12 | 1 | |||
There has been expended on the new Steamer “Pharos,” £18,977 : 6 : 7.
The Commissioners have purchased a House at Crail for £105 : 19 : 4 for the use of the Boatmen attending at the Isle of May.
The attention of the Commissioners is called to the circumstance that a complete change has been made this year in the mode of stating the Accounts. The Accounts are now, for the first time, concentrated in the Secretary’s department, and for every item entered in the subjoined abstract, reference is now, and will hereafter, be made to a page of the Ledger containing a detailed account vouching the charge. Following out this arrangement, the account has been branched into three heads or divisions.[417] The first head comprises the ordinary expenses of the Lighthouses. In this branch it has been thought right to state separately, under the head of the Isle of May, the interest on the debt to Government, being the balance of the price of the Island. The second head comprises the ordinary expenses of the Board, not in the first instance chargeable against any particular Lighthouse, but falling to be afterwards allocated in the final view of the Receipt and Expenditure of each Lighthouse. This branch is again subdivided so as to shew—
| 1. | The Expense of Collection. |
| 2. | Repayments, &c. of Light-Duties overcharged. |
| 3. | The Expense of the Establishment, including Salaries, Stationery, &c. |
| 4. | The Shipping Establishment. |
| 5. | Beacons and Buoys—ordinary maintenance. |
| 6. | The Storehouse, Leith. |
| 7. | Charities and Superannuations. |
| 8. | Miscellaneous Payments. |
The last division of the abstract comprises what is termed the extraordinary expenditure, that is, the expense of New Works and others not falling to be allocated upon the Lighthouses.
In effecting this change, various payments which appeared in the former abstracts will not now be found in the present, such as Rents and Feu-duties, which are now charged to the respective Lighthouses for which they are paid; the Storekeeper’s Salary, which is stated in the Storehouse Account; the Office-Keeper’s, in the Office Account, &c., and the Salaries of the Officers of the Board will be found under the head of Edinburgh Establishment.
[418]
ABSTRACT of the Receipts and Payments on Account of the Duties levied for the Northern Lighthouses for the year 1846.
| RECEIPTS. | |||||||||||||||
| I. | Gross Amount of the Duties received for 1846, per State, No. I. p. 429, | £46,001 | 11 | 2 | ⁶⁄₈ | ||||||||||
| Which has been received in the following proportions for each Lighthouse, as appears from State, No. II., pp. 430-3, viz.:— | |||||||||||||||
| 1. | Inchkeith, | £2524 | 9 | 2 | ²⁄₈ | ||||||||||
| 2. | Isle of May, | 3825 | 8 | 5 | ⁴⁄₈ | ||||||||||
| 3. | Bell Rock, | 5342 | 15 | 5 | ⁴⁄₈ | ||||||||||
| 4. | Girdleness, | 2458 | 4 | 5 | ⁴⁄₈ | ||||||||||
| 5. | Buchanness, | 1880 | 1 | 3 | ⁴⁄₈ | ||||||||||
| 6. | Kinnairdshead, | 1744 | 11 | 3 | ⁴⁄₈ | ||||||||||
| 7. | Tarbetness, | 329 | 17 | 4 | ⁶⁄₈ | ||||||||||
| 8. | Sumburghhead, | 286 | 18 | 2 | ⁶⁄₈ | ||||||||||
| 9. | Startpoint, | 1154 | 5 | 4 | ²⁄₈ | ||||||||||
| 10. | Pentland Skerries, | 1370 | 10 | 5 | ⁶⁄₈ | ||||||||||
| 11. | Dunnethead, | 1311 | 1 | 10 | ²⁄₈ | ||||||||||
| 12. | Capewrath, | 1278 | 9 | 9 | |||||||||||
| 13. | Island Glass, | 679 | 1 | 10 | ⁶⁄₈ | ||||||||||
| 14. | Barrahead, | 1063 | 3 | 2 | ⁶⁄₈ | ||||||||||
| 15. | Skerryvore, | 2090 | 11 | 3 | ⁴⁄₈ | ||||||||||
| 16. | Lismore, | 239 | 11 | 4 | |||||||||||
| 17. | Rhinns of Islay, | 1414 | 5 | 8 | ⁶⁄₈ | ||||||||||
| 18. | Mull of Kintyre, | 1549 | 0 | 1 | |||||||||||
| 19. | Pladda, | 2762 | 14 | 3 | ⁷⁄₈ | ||||||||||
| 20. | Corsewall, | 2811 | 5 | 3 | ⁶⁄₈ | ||||||||||
| 21. | Mull of Galloway, | 2823 | 19 | 8 | ⁶⁄₈ | ||||||||||
| 22. | Little Ross, | 1187 | 7 | 9 | ⁴⁄₈ | ||||||||||
| 23. | Point of Ayre, | 1755 | 17 | 5 | ⁴⁄₈ | ||||||||||
| 24. | Calf of Man (two Lights), | 3839 | 2 | 11 | ²⁄₈ | ||||||||||
| 25. | Covesea Skerries, | 193 | 7 | 0 | |||||||||||
| 26. | Cromarty, | 27 | 14 | 11 | |||||||||||
| 27. | Chanonry, | 57 | 15 | 1 | |||||||||||
| £46,001 | 11 | 3 | ⁷⁄₈ | ||||||||||||
| Deduct fractions short credited by Bankers, | 0 | 0 | 1 | ¹⁄₈ | |||||||||||
| As above, | £46,001 | 11 | 2 | ⁶⁄₈ | |||||||||||
| II. | Miscellaneous Receipts— | ||||||||||||||
| Folio in Ledger. |
|||||||||||||||
| 32 & 73 | Rent of Stable behind the Office, | £18 | 0 | 0 | |||||||||||
| 73 | Do. of Small Houses at Arbroath, | 5 | 5 | 0 | |||||||||||
| 33 | Proceeds sale of Regent Tender, | 485 | 14 | 3 | |||||||||||
| 32 | Composition of 1s. 6d. per pound from the Trustee on Andrew Greig’s Bankrupt Estate, on a claim of £340, 11s. 8d. and Expenses arising from an evasion of Light-dues, | 27 | 0 | 9 | |||||||||||
| 30 | Price of Lighter sold to Kirkcaldy Harbour Commissioners, [419] | 60 | 0 | 0 | |||||||||||
| 74 | Do. do. to Leith Shipping Company, | 45 | 0 | 0 | |||||||||||
| 40 | Do. of Horse sold at Barrahead, | 10 | 0 | 0 | |||||||||||
| ... | Do. of an Ass sold at Inchkeith, | 0 | 9 | 6 | |||||||||||
| 149 | Do. of Articles sold at Skerryvore, | 126 | 5 | 10 | |||||||||||
| 73,75, & 315 | Fines imposed on Light-keepers, received, | 13 | 1 | 8 | |||||||||||
| 74 | Sum received from the General Post-Office, for the maintenance of the Harbour Light at Portpatrick for the year 1845, | 136 | 10 | 9 | |||||||||||
| 40 & 75 | Interest received from the Royal Bank on money deposited, | 966 | 9 | 9 | |||||||||||
| Sum, | 1893 | 17 | 6 | ||||||||||||
| Sums of Receipts carried to Abstract, page 425, | £47,895 | 8 | 8 | ⁶⁄₈ | |||||||||||
| PAYMENTS. | |||||||||||||||
| Folio in Ledger. |
BRANCH I.—Ordinary Expenses of the Board, being the Maintenance of the Lights for the year, viz:— | ||||||||||||||
| 1. Lighthouses— | |||||||||||||||
| 326 | 1. | Inchkeith, | £583 | 5 | 10 | ¹⁄₂ | |||||||||
| 327 | 2. | Isle of May, | £702 | 3 | 9 | ||||||||||
| Isle of May, Year’s Interest to Government, | 250 | 0 | 0 | ||||||||||||
| 952 | 3 | 9 | |||||||||||||
| 355 | 3. | Bell Rock, | 989 | 1 | 3 | ¹⁄₄ | |||||||||
| 329 | 4. | Girdleness, | 548 | 18 | 1 | ||||||||||
| 330 | 5. | Buchanness, | 623 | 5 | 3 | ||||||||||
| 331 | 6. | Kinnairdshead, | 578 | 10 | 0 | ¹⁄₂ | |||||||||
| 332 | 7. | Tarbetness, | 574 | 11 | 11 | ||||||||||
| 333 | 8. | Sumburghhead, | 597 | 5 | 3 | ³⁄₄ | |||||||||
| 334 | 9. | Startpoint, | 347 | 0 | 8 | ||||||||||
| 335 | 10. | Pentland Skerries (two Lights), | 851 | 8 | 11 | ||||||||||
| 336 | 11. | Dunnethead, | 470 | 19 | 7 | ¹⁄₂ | |||||||||
| 337 | 12. | Capewrath, | 587 | 6 | 11 | ¹⁄₄ | |||||||||
| 338 | 13. | Island Glass, | 515 | 2 | 10 | ¹⁄₄ | |||||||||
| 339 | 14. | Barrahead, | 594 | 3 | 10 | ¹⁄₂ | |||||||||
| 357 | 15. | Skerryvore, | 1122 | 0 | 7 | ||||||||||
| 340 | 16.[420] | Lismore, | 515 | 14 | 2 | ¹⁄₄ | |||||||||
| 341 | 17. | Rhinns of Islay, | 569 | 12 | 7 | ³⁄₄ | |||||||||
| 342 | 18. | Mull of Kintyre, | 554 | 17 | 10 | ¹⁄₂ | |||||||||
| 343 | 19. | Pladda, | 584 | 10 | 10 | ||||||||||
| 344 | 20. | Corsewall, | 465 | 13 | 4 | ||||||||||
| 345 | 21. | Mull of Galloway, | 517 | 0 | 5 | ¹⁄₂ | |||||||||
| 346 | 22. | Little Ross, | 516 | 18 | 6 | ¹⁄₄ | |||||||||
| 347 | 23. | Point of Ayre, | 409 | 1 | 4 | ¹⁄₂ | |||||||||
| 348 | 24. | Calf of Man (High Tower), | £394 | 4 | 7 | ||||||||||
| 354 | 25. | Calf of Man (Low Tower), | 419 | 14 | 10 | ||||||||||
| 813 | 19 | 5 | |||||||||||||
| 351 | 26. | Covesea Skerries, | 419 | 16 | 8 | ¹⁄₂ | |||||||||
| 358 | 27. | Cromarty, | 339 | 17 | 3 | ||||||||||
| 353 | 28. | Chanonry, | 284 | 7 | 1 | ||||||||||
| 350 | 29. | Loch Ryan, | 176 | 5 | 7 | ||||||||||
| Sum,—Carried to Abstract, p. 425, | £16,103 | 0 | 2 | ³⁄₄ | |||||||||||
| BRANCH II.—Ordinary Expenses falling to be allocated upon each Lighthouse— | |||||||||||||||
| 1. Expense of Collection— | |||||||||||||||
| To paid Commission to Collectors, per State, No. I. p. 429, | £2401 | 7 | 3 | ⁴⁄₈ | |||||||||||
| To paid Commission to Bankers, | 115 | 3 | 7 | ||||||||||||
| £2516 | 10 | 10 | ⁴⁄₈ | ||||||||||||
| 2. Repayments, &c., of Light-Duties overcharged, | 218 | 16 | 10 | ²⁄₈ | |||||||||||
| 3. Establishment in Edinburgh— | |||||||||||||||
| Engineer, ³⁄₄ Salary at £900, | £675 | 0 | 0 | ||||||||||||
| Engineer, ¹⁄₄ Salary at £1200, | 300 | 0 | 0 | ||||||||||||
| £975 | 0 | 0 | |||||||||||||
| Secretary, | 500 | 0 | 0 | ||||||||||||
| Accountant, Salary to 8th July, when he died, | 84 | 12 | 0 | ||||||||||||
| Superintendent of Light-keepers, ³⁄₄ Salary at £145, | £108 | 15 | 0 | ||||||||||||
| Superintendent of Light-keepers, ¹⁄₄ Salary at £210, | 52 | 10 | 0 | ||||||||||||
| 161 | 5 | 0 | |||||||||||||
| Foreman of Lightroom repairs, ³⁄₄ Salary at £110, | £82 | 10 | 0 | ||||||||||||
| Foreman of Lightroom repairs, ¹⁄₄ Salary at £140, | 35 | 0 | 0 | ||||||||||||
| 117 | 10 | 0 | |||||||||||||
| Engineer’s Clerk, ¹⁄₄ Salary (formerly paid by Engineer), | 32 | 10 | 0 | ||||||||||||
| Examiner of Accounts, from 8th January to Candlemas, | 17 | 2 | 6 | ||||||||||||
| First Clerk in Secretary’s Department, ¹⁄₄ Salary, | 25 | 0 | 0 | ||||||||||||
| Second Clerk in Secretary’s Department, ¹⁄₄ Salary, | 25 | 0 | 0 | ||||||||||||
| Officer (now conjoined with Housekeeper), ¹⁄₄ Salary,[421] | 5 | 0 | 0 | ||||||||||||
| Payments to two Clerks in Accountant’s Department, to cease at Whitsunday in consequence of the appointments in Secretary’s Department, | 174 | 6 | 0 | ||||||||||||
| Interim Accountant, per minute of the Board, until Examiner of Accounts was appointed, | 105 | 0 | 0 | ||||||||||||
| Office, including Porter and House-Servants’ Wages, House Expenses, Taxes, Books for Library, &c., | 910 | 10 | 3 | ¹⁄₂ | |||||||||||
| 279 | 3132 | 15 | 9 | ¹⁄₂ | |||||||||||
| 4. Shipping Establishment— | |||||||||||||||
| 132 | Pharos Steam-Vessel, | £3790 | 1 | 11 | ³⁄₄ | ||||||||||
| 133 | Prince of Wales, Bell Rock Tender, | 954 | 10 | 2 | |||||||||||
| 135 | Francis, Skerryvore Tender, | 920 | 17 | 6 | ¹⁄₂ | ||||||||||
| 137 | Regent Tender (now sold), | 259 | 3 | 7 | |||||||||||
| 5924 | 13 | 3 | ³⁄₄ | ||||||||||||
| 5. Beacons and Buoys—Expense of Ordinary Maintenance, | 91 | 7 | 0 | ||||||||||||
| 6. Storehouse, Leith, including Storekeeper’s Salary, Taxes, Freight of Stores, &c., viz:— | |||||||||||||||
| Salary, ³⁄₄, | £40 | 13 | 0 | ||||||||||||
| Salary, ¹⁄₄, at £100 per annum, | 25 | 0 | 0 | ||||||||||||
| £65 | 13 | 0 | |||||||||||||
| Expenses of House, Packing Stores, &c., | 145 | 9 | 7 | ¹⁄₄ | |||||||||||
| 184 | Freight of Stores, | 133 | 4 | 3 | ¹⁄₂ | ||||||||||
| 344 | 6 | 10 | ³⁄₄ | ||||||||||||
| 7. Charities and Superannuations to Retired Servants of the Board, viz.:— | |||||||||||||||
| 1. | Prior to the last Act of Parliament— | ||||||||||||||
| William Tweedy, one year’s Annuity, | £20 | 0 | 0 | ||||||||||||
| Mrs Leask, one year’s Annuity | 10 | 0 | 0 | ||||||||||||
| Hugh Rose, one year’s Annuity | 20 | 0 | 0 | ||||||||||||
| Jane Walker, one year’s Annuity (died March 13, 1847), | 6 | 6 | 0 | ||||||||||||
| Euphemia Poole, one year’s Annuity, | 5 | 0 | 0 | ||||||||||||
| 61 | 6 | 0 | |||||||||||||
| 2. | Since last Act, viz.: | ||||||||||||||
| Robert Stevenson, Esq., late Engineer, | £580 | 0 | 0 | ||||||||||||
| Matthew Harvie, Light-keeper, | 69 | 7 | 6 | ||||||||||||
| John Bruce, late Officer, | 13 | 0 | 0 | ||||||||||||
| George Kirk, Light-keeper, | 40 | 0 | 0 | ||||||||||||
| John Watt, Light-keeper, (died Dec. 1846), | 41 | 12 | 6 | ||||||||||||
| William Heddle, Light-keeper,[422] | 17 | 15 | 0 | ||||||||||||
| Robert Selkirk, Light-keeper, (died Jan. 1847), | 20 | 16 | 4 | ||||||||||||
| Andrew Adamson, Light-keeper, | 47 | 0 | 0 | ||||||||||||
| James Brown jun., Light-keeper, | 29 | 11 | 8 | ||||||||||||
| William Soutar, Light-keeper, | 48 | 10 | 0 | ||||||||||||
| John Murray, late Boatman, Isle of May, | 18 | 6 | 8 | ||||||||||||
| David Lyall, Light-keeper, | 43 | 0 | 0 | ||||||||||||
| Thomson Milne, Light-keeper, | 64 | 1 | 0 | ||||||||||||
| David Laughton, Light-keeper, | 47 | 10 | 0 | ||||||||||||
| Alexander Burnett, Light-keeper, | 45 | 0 | 0 | ||||||||||||
| James Wallace, | 34 | 0 | 0 | ||||||||||||
| John Miller (proportion till date of death), | 11 | 12 | 0 | ||||||||||||
| Mrs Duncan, late Housekeeper, three-quarters, | 10 | 10 | 0 | ||||||||||||
| John Scott, late Mate, Prince of Wales, quarter to Martinmas last, | 22 | 10 | 8 | ||||||||||||
| C. Cunningham, Esq., late Secretary, from 21st December to Candlemas, | 45 | 7 | 3 | ||||||||||||
| 1249 | 9 | 11 | |||||||||||||
| 8. Miscellaneous Expenses not appropriated to any Particular Head, | 2420 | 19 | 5 | ||||||||||||
| Being— | |||||||||||||||
| 1. | For Educating Expectant Light-keepers, being their Travelling Charges and Subsistence, | £84 | 16 | 0 | |||||||||||
| 2. | Travelling Expenses of the Board, | 128 | 18 | 11 | |||||||||||
| 3. | Travelling Expenses of Officers on the Business of the Board, | 513 | 3 | 9 | |||||||||||
| 4. | Half-yearly Dinner Bills, £69, 5s., and £86 : 2 : 6, | 155 | 7 | 6 | |||||||||||
| 5. | Advertising Reduction of Duties, | 90 | 10 | 10 | |||||||||||
| 6. | Printing Expenses, viz., New Tables, Notices, Circulars, &c., | £173 | 5 | 7 | |||||||||||
| Printing Expenses, 500 vols. Collector’s Receipt Books, &c., | 146 | 19 | 6 | ||||||||||||
| Printing Expenses, Annual List of Lighthouses, &c., | 207 | 10 | 10 | ||||||||||||
| Printing Expenses, “Stevenson on Lenses,” and Expenses connected with Lenses, | 31 | 1 | 5 | ||||||||||||
| 558 | 17 | 4 | |||||||||||||
| 7. | Making Oil Casks, and Cooperage of old do. | 145 | 11 | 2 | |||||||||||
| 8. | Postages and Carriage of Parcels,[423] | 120 | 18 | 10 | |||||||||||
| 9. | Messrs Cuningham and Bell, W.S., Law-Agents, Account for Commissions to and Bonds by Collectors, &c., | 136 | 4 | 0 | |||||||||||
| 10. | Messrs Spottiswoode and Robertson, Solicitors, London, | 57 | 11 | 8 | |||||||||||
| 11. | Gratuity to Lewis Proctor, an occasional Light-keeper, who met with a severe Accident by a fall from the Lighthouse at Kinnairdshead, | 30 | 0 | 0 | |||||||||||
| 12. | Medical Attendance on Keepers’ Families at Insulated Stations, | 26 | 17 | 0 | |||||||||||
| 13. | Paid for Nomination to Edinburgh Royal Lunatic Asylum for Keeper’s Wife at Chanonry Lighthouse, | 12 | 10 | 0 | |||||||||||
| 14. | Gratuities voted to aged Light-keepers to meet Insurances on their Lives, | 38 | 7 | 1 | |||||||||||
| 15. | Sundry small Sums due by Light-keepers, connected with Insurances on their Lives, and Stamps for Premiums, | 37 | 2 | 8 | |||||||||||
| 16. | R. W. Swinburne and Co., Newcastle, Plate-Glass, | 32 | 1 | 6 | |||||||||||
| 17. | Paid for Temporary Lanterns during Repairs of Lighthouses, | 64 | 17 | 7 | |||||||||||
| 18. | One Dozen Stamped Receipt-Books for Keepers’ Salaries, and Fees getting same Stamped in London, | 7 | 1 | 0 | |||||||||||
| 19. | Expenses incurred by Henry Banks, tailor, in visiting the different Lighthouses, and taking “measures” for Clothing the Keepers, | 38 | 0 | 2 | |||||||||||
| 20. | Periodicals furnished to the Keepers, | 4 | 14 | 7 | |||||||||||
| 21. | A Copper Buoy, | 3 | 16 | 11 | |||||||||||
| 22. | Repairs on Rankin Lighter, | 5 | 2 | 4 | |||||||||||
| 23. | Account connected with Skerryvore Lighters, | 6 | 7 | 0 | |||||||||||
| 24. | Models of Dioptric Light, | 83 | 13 | 1 | |||||||||||
| 25. | Freight to London, Leith, Edinburgh, and Glasgow Shipping Company, | 3 | 1 | 5 | |||||||||||
| 26. | Various small items for Lithographing, &c. &c., | 35 | 7 | 1 | |||||||||||
| Sum as on preceding page, | £2420 | 19 | 5 | ||||||||||||
| Carry forward, | £15,960 | 6 | 0 | ²⁄₈ | |||||||||||
| Ordinary Expenses brought forward,[424] | £15,960 | 6 | 0 | ²⁄₈ | |||||||||||
| Which have been Allocated to each Lighthouse in the proportions following, as appears from State, No. II., pp. 430-3, viz.— | |||||||||||||||
| 1. | Inchkeith, | £577 | 15 | 9 | ²⁄₈ | ||||||||||
| 2. | Isle of May, | 941 | 8 | 6 | |||||||||||
| 3. | Bell Rock, | 977 | 17 | 9 | |||||||||||
| 4. | Girdleness, | 544 | 5 | 8 | |||||||||||
| 5. | Buchanness, | 617 | 4 | 1 | ⁶⁄₈ | ||||||||||
| 6. | Kinnairdshead, | 573 | 16 | 11 | ²⁄₈ | ||||||||||
| 7. | Tarbetness, | 569 | 18 | 1 | ²⁄₈ | ||||||||||
| 8. | Sumburghhead, | 591 | 11 | 8 | ⁴⁄₈ | ||||||||||
| 9. | Startpoint, | 345 | 4 | 4 | ⁴⁄₈ | ||||||||||
| 10. | Pentland Skerries, | 841 | 17 | 10 | ⁴⁄₈ | ||||||||||
| 11. | Dunnethead, | 467 | 8 | 4 | |||||||||||
| 12. | Capewrath, | 581 | 14 | 7 | ²⁄₈ | ||||||||||
| 13. | Island Glass, | 510 | 15 | 6 | ⁴⁄₈ | ||||||||||
| 14. | Barrahead, | 588 | 12 | 7 | |||||||||||
| 15. | Skerryvore, | 1108 | 19 | 1 | |||||||||||
| 16. | Lismore, | 511 | 15 | 4 | ⁴⁄₈ | ||||||||||
| 17. | Rhinns of Islay, | 564 | 19 | 6 | ⁶⁄₈ | ||||||||||
| 18. | Mull of Kintyre, | 550 | 3 | 10 | ⁶⁄₈ | ||||||||||
| 19. | Pladda, | 579 | 15 | 2 | ²⁄₈ | ||||||||||
| 20. | Corsewall, | 462 | 9 | 9 | ⁴⁄₈ | ||||||||||
| 21. | Mull of Galloway, | 512 | 14 | 11 | ⁴⁄₈ | ||||||||||
| 22. | Little Ross, | 512 | 14 | 11 | ²⁄₈ | ||||||||||
| 23. | Point of Ayre, | 406 | 6 | 4 | ⁴⁄₈ | ||||||||||
| 24. | Calf of Man (two Lights), | 805 | 8 | 7 | ⁴⁄₈ | ||||||||||
| 25. | Covesea Skerries, | 417 | 3 | 1 | ⁶⁄₈ | ||||||||||
| 26. | Cromarty, | 338 | 6 | 4 | ⁶⁄₈ | ||||||||||
| 27. | Chanonry, | 283 | 2 | 8 | ⁴⁄₈ | ||||||||||
| 28. | Loch Ryan, | 176 | 14 | 1 | |||||||||||
| As above, | 15,960 | 6 | 0 | ²⁄₈ | |||||||||||
| BRANCH III.—Extraordinary Expenses not Allocated to each Lighthouse:— | |||||||||||||||
| 189 | To paid for new Steamer Pharos, | £7548 | 13 | 7 | |||||||||||
| 310 | Expense of Harbour Light at Portpatrick, | 129 | 17 | 4 | ¹⁄₄ | ||||||||||
| 182 | Expense connected with Skerryvore Book, | 199 | 18 | 0 | |||||||||||
| 33 | To paid for House in Crail for use of Isle of May Boatmen, and Fees connected with Purchase, | 105 | 19 | 4 | |||||||||||
| £7984 | 8 | 3 | ¹⁄₄ | ||||||||||||
| Expense of New Works, viz.:— | |||||||||||||||
| 150 | Skerryvore, | £227 | 8 | 2 | |||||||||||
| 287 | Bo Pheg Beacon, | 25 | 10 | 1 | |||||||||||
| 284 | Covesea,[425] | 1109 | 5 | 4 | |||||||||||
| 296 | Cromarty, | 342 | 9 | 3 | |||||||||||
| 298 | Chanonry, | 405 | 7 | 8 | |||||||||||
| 300 | Ardnamurchan, | 2343 | 17 | 6 | |||||||||||
| 314 | Laggan Spur Beacon, | 748 | 10 | 6 | |||||||||||
| 316 | Island Glass, | 1797 | 3 | 5 | ¹⁄₂ | ||||||||||
| 319 | Nosshead, | 1467 | 6 | 1 | |||||||||||
| 322 | Loch Ryan, | 829 | 12 | 9 | ¹⁄₂ | ||||||||||
| 121 | Loch Ryan, Beacon, | 152 | 5 | 9 | |||||||||||
| 324 | Pentland Skerries new Works, | 3135 | 17 | 5 | ¹⁄₂ | ||||||||||
| 145 | Pentland Skerries Dioptric Light, | 2037 | 11 | 4 | |||||||||||
| 308 | Renewal of Fixed Lights, | 3035 | 14 | 4 | |||||||||||
| 106 | Campbeltown Beacons, | 17 | 4 | 10 | |||||||||||
| ... | Lapock Beacon, | 8 | 12 | 5 | |||||||||||
| 117 | Startpoint New Works, | 5 | 19 | 4 | |||||||||||
| 118 | Elie or Vow’s Beacon, | 205 | 5 | 8 | |||||||||||
| 119 | Whiteness Beacon, | 152 | 5 | 8 | |||||||||||
| 120 | Longman’s Point Beacon,, | 164 | 15 | 6 | |||||||||||
| 184 | Brist Beacon, | 8 | 12 | 5 | |||||||||||
| 306 | Mull of Kintyre Dykes and Road, | 647 | 17 | 9 | |||||||||||
| 286 | Buoys, | 1458 | 7 | 11 | ¹⁄₂ | ||||||||||
| Sum, | 20,327 | 1 | 3 | ||||||||||||
| Carried to Abstract below, | £28,311 | 9 | 6 | ¹⁄₄ | |||||||||||
| ABSTRACT OF THE PRECEDING ACCOUNT. | |||||||||||||||
| RECEIPTS:— | |||||||||||||||
| Branch III.—Gross Amount of the Duties received for 1846, p. 418, | £46,001 | 11 | 2 | ⁶⁄₈ | |||||||||||
| Branch III.—Miscellaneous Receipts, p. 419, | 1,893 | 17 | 6 | ||||||||||||
| £47,895 | 8 | 8 | ⁶⁄₈ | ||||||||||||
| PAYMENTS:— | |||||||||||||||
| Branch III.—Ordinary Expenses, being the Maintenance of Lights, &c. p. 420, | £16,103 | 0 | 2 | ³⁄₄ | |||||||||||
| Branch III.—Ordinary Expenses, falling to be allocated upon each Lighthouse, p. 424, | 15,960 | 6 | 0 | ¹⁄₄ | |||||||||||
| Branch III.—Extraordinary Expenses not allocated to each Lighthouse, as above, | 28,311 | 9 | 6 | ¹⁄₄ | |||||||||||
| 60,374 | 15 | 9 | ²⁄₈ | ||||||||||||
| Balance superexpended in 1846, | £12,479 | 7 | 0 | ⁴⁄₈ | |||||||||||
| Balance on hand at 31st March 1846, | 42,069 | 6 | 10 | ||||||||||||
| Balance on hand at 31st March 1847, | £29,589 | 19 | 9 | ¹⁄₂ | |||||||||||
| Whereof— | |||||||||||||||
| In the Royal Bank, | £28,944 | 16 | 8 | ||||||||||||
| In Secretary’s Account, | 40 | 16 | 11 | ||||||||||||
| £28,985 | 13 | 7 | |||||||||||||
| 89 | Balance due by Peter Grant, Superintendent, Nosshead, | 203 | 10 | 2 | |||||||||||
| 157 | Balance due by Master of Prince of Wales Tender, | 35 | 3 | 4 | |||||||||||
| 161 | Balance due by Steward of Pharos Steamer, | 30 | 19 | 2 | |||||||||||
| 164 | Balance due by Master of Francis, Skerryvore Tender, | 2 | 12 | 5 | |||||||||||
| 166 | Balance due by Superintendent of Light-keepers, | 11 | 11 | 2 | |||||||||||
| 168 | Balance due by Foreman of Light-room Repairs, | 5 | 3 | 5 | |||||||||||
| 172 | Balance due by Buoymaster, | 5 | 1 | 6 | |||||||||||
| 176 | Balance due by Store-keeper, | 7 | 17 | 0 | |||||||||||
| 180 | Balance due by Thomas Hope, Superintendent, Island Glass, | 87 | 17 | 7 | ¹⁄₂ | ||||||||||
| 307 | Balance due by Master of Pharos, | 5 | 10 | 8 | |||||||||||
| 318 | Balance due by James Scott, Superintendent, Pentland Skerries, | 188 | 12 | 3 | |||||||||||
| Folio in Small Ledger. | |||||||||||||||
| 6 | Sum due by Robert Selkirk’s Representatives, to be paid when Insurance money is received, | 10 | 0 | 0 | |||||||||||
| 8 | Balance due by Richard Cumming, Light-keeper, | 2 | 13 | 0 | |||||||||||
| 9 | Balance due by James Laughton, do., | 3 | 0 | 0 | |||||||||||
| 10 | Balance due by William Kirk, do., | 4 | 14 | 6 | |||||||||||
| Equal to Balance, | 29,589 | 19 | 9 | ¹⁄₂ | |||||||||||
Edinburgh, 5th May 1847.—Prepared and Reported by
(Signed) ALEX. CUNINGHAM, Secretary.
84 George Street,
Edinburgh, 25th May 1847.
In obedience to the Remit by the Honourable Board of Commissioners of Northern Lighthouses, I have carefully audited the Accounts of the Board for the year ending 31st March 1847; and I have to report, that the Accounts are clearly and accurately stated—that they are fully vouched—and that, in my humble opinion, the Report of the Secretary contains a very distinct statement of the Intromissions of the Board during the above period.
(Signed) KENNETH MACKENZIE, Accountant.
[427]
STATEMENTS ANNEXED TO THE SECRETARY’S REPORT FOR 1846.
No. I.—Account of Northern Light-Duties received in the Year 1846.
| Gross Receipts. |
Commission to Collectors. |
Repayments, &c. |
Nett Duties Received. |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Aberdeen, | £2243 | 3 | 9 | ⁴⁄₈ | £121 | 11 | 8 | ⁴⁄₈ | £5 | 14 | 5 | £2115 | 17 | 8 | ||
| 2. | Alloa, | 402 | 6 | 1 | ⁴⁄₈ | 23 | 6 | 8 | 6 | 17 | 9 | 372 | 1 | 8 | ⁴⁄₈ | ||
| 3. | Arbroath, | 254 | 2 | 11 | ⁶⁄₈ | 12 | 17 | 2 | ⁶⁄₈ | 3 | 17 | 7 | ²⁄₈ | 237 | 8 | 1 | ⁶⁄₈ |
| 4. | Ayr, | 158 | 12 | 11 | 8 | 1 | 10 | 1 | 15 | 10 | 148 | 15 | 3 | ||||
| 5. | Aberystwith, | 6 | 17 | 6 | ⁴⁄₈ | 0 | 6 | 9 | ⁴⁄₈ | 0 | 1 | 0 | 6 | 9 | 9 | ||
| 6. | Arundel, | ... | ... | ... | ... | ||||||||||||
| 7. | Banff, | 467 | 7 | 5 | 28 | 17 | 6 | 2 | 19 | 3 | 435 | 10 | 8 | ||||
| 8. | Borrowstounness, | 675 | 6 | 1 | ⁴⁄₈ | 48 | 11 | 9 | ⁴⁄₈ | 9 | 4 | 1 | 617 | 10 | 3 | ||
| 9. | Barnstaple, | 1 | 7 | 2 | ⁴⁄₈ | 0 | 1 | 4 | ⁴⁄₈ | ... | 1 | 5 | 10 | ||||
| 10. | Beaumaris, | 123 | 17 | 1 | ⁴⁄₈ | 6 | 12 | 7 | ⁴⁄₈ | 0 | 15 | 1 | 116 | 9 | 5 | ||
| 11. | Berwick, | 121 | 0 | 8 | ⁴⁄₈ | 6 | 11 | 9 | ⁴⁄₈ | 0 | 1 | 8 | 114 | 7 | 3 | ||
| 12. | Bideford, | 8 | 14 | 11 | 0 | 8 | 9 | ... | 8 | 6 | 2 | ||||||
| 13. | Boston, | 9 | 15 | 0 | ⁴⁄₈ | 0 | 10 | 7 | ⁴⁄₈ | 0 | 5 | 6 | 8 | 18 | 11 | ||
| 14. | Bridgewater, | 12 | 0 | 7 | ⁷⁄₈ | 0 | 11 | 11 | ⁷⁄₈ | 0 | 2 | 10 | 11 | 5 | 10 | ||
| 15. | Bridlington, | 26 | 1 | 3 | ⁴⁄₈ | 1 | 6 | 1 | ... | 24 | 15 | 2 | ⁴⁄₈ | ||||
| 16. | Bridport, | 2 | 18 | 0 | ⁴⁄₈ | 0 | 2 | 10 | ⁴⁄₈ | ... | 2 | 15 | 2 | ||||
| 17. | Bristol, | 124 | 12 | 7 | ²⁄₈ | 6 | 4 | 6 | ⁶⁄₈ | 0 | 14 | 0 | 117 | 14 | 0 | ⁴⁄₈ | |
| 18. | Baltimore, | ... | ... | ... | ... | ||||||||||||
| 19. | Belfast, | 2446 | 1 | 4 | ²⁄₈ | 125 | 6 | 4 | ²⁄₈ | 56 | 12 | 10 | 2264 | 2 | 2 | ||
| 20. | Campbeltown, | 82 | 14 | 9 | ⁴⁄₈ | 5 | 2 | 1 | ⁴⁄₈ | 1 | 12 | 8 | 76 | 0 | 0 | ||
| 21. | Caernarvon, | 25 | 13 | 10 | 1 | 7 | 7 | 0 | 8 | 0 | 23 | 18 | 3 | ||||
| 22. | Cardiff, | 110 | 19 | 7 | 5 | 11 | 0 | ... | 105 | 8 | 7 | ||||||
| 23. | Cardigan, | 1 | 7 | 11 | ⁴⁄₈ | 0 | 1 | 7 | ⁴⁄₈ | ... | 1 | 6 | 4 | ||||
| 24. | Carlisle, | 84 | 0 | 3 | ²⁄₈ | 4 | 7 | 9 | ²⁄₈ | 0 | 10 | 5 | 79 | 2 | 1 | ||
| 25. | Chepstow, | 0 | 14 | 11 | 0 | 0 | 9 | ... | 0 | 14 | 2 | ||||||
| 26. | Chester, | 158 | 4 | 5 | ¹⁄₈ | 8 | 1 | 5 | ³⁄₈ | 1 | 0 | 0 | 149 | 2 | 11 | ⁶⁄₈ | |
| 27. | Chichester, | 2 | 15 | 6 | ²⁄₈ | 0 | 3 | 9 | ²⁄₈ | ... | 2 | 11 | 9 | ||||
| 28. | Clay, | 1 | 2 | 6 | 0 | 1 | 8 | ⁴⁄₈ | ... | 1 | 0 | 9 | ⁴⁄₈ | ||||
| 29. | Colchester, | ... | ... | ... | ... | ||||||||||||
| 30. | Cowes, | ... | ... | ... | ... | ||||||||||||
| 31. | Coleraine, | 101 | 5 | 8 | ⁴⁄₈ | 5 | 1 | 7 | ... | 96 | 4 | 1 | ⁴⁄₈ | ||||
| 32. | Cork, | 70 | 13 | 1 | 3 | 10 | 6 | 2 | 0 | 9 | 65 | 1 | 10 | ||||
| 33. | Dunbar, | 115 | 11 | 11 | 7 | 1 | 2 | 0 | 11 | 4 | 107 | 19 | 5 | ||||
| 34. | Dundee, | 2062 | 9 | 10 | 105 | 7 | 2 | 7 | 15 | 10 | 1949 | 6 | 10 | ||||
| 35. | Dumfries, | 351 | 10 | 6 | ⁴⁄₈ | 24 | 13 | 0 | ⁴⁄₈ | 2 | 10 | 8 | 324 | 6 | 10 | ||
| 36. | Dartmouth, | ... | ... | ... | ... | ||||||||||||
| 37. | Deal, | ... | ... | ... | ... | ||||||||||||
| 38. | Dover,[428] | 0 | 8 | 0 | ⁴⁄₈ | 0 | 0 | 5 | ... | 0 | 7 | 7 | ⁴⁄₈ | ||||
| 39. | Dublin, | 2256 | 17 | 10 | 114 | 0 | 9 | 9 | 16 | 9 | 2133 | 0 | 4 | ||||
| 40. | Drogheda, | 149 | 8 | 2 | ⁴⁄₈ | 7 | 9 | 5 | ... | 141 | 18 | 9 | ⁴⁄₈ | ||||
| 41. | Dundalk, | 120 | 6 | 6 | ⁴⁄₈ | 6 | 0 | 3 | ⁴⁄₈ | 0 | 6 | 8 | 113 | 19 | 7 | ||
| 42. | Exeter, | 2 | 17 | 5 | ⁴⁄₈ | 0 | 3 | 0 | ⁴⁄₈ | ... | 2 | 14 | 5 | ||||
| 43. | Fisherrow, | 219 | 0 | 8 | ⁶⁄₈ | 13 | 12 | 4 | ⁴⁄₈ | 0 | 15 | 3 | 204 | 13 | 1 | ²⁄₈ | |
| 44. | Falmouth, | ... | ... | ... | ... | ||||||||||||
| 45. | Faversham, | ... | ... | ... | ... | ||||||||||||
| 46. | Fowey, | 2 | 4 | 11 | 0 | 3 | 0 | ⁴⁄₈ | ... | 2 | 1 | 10 | ⁴⁄₈ | ||||
| 47. | Glasgow, | 3599 | 16 | 10 | 182 | 14 | 4 | ⁴⁄₈ | 11 | 15 | 11 | ⁴⁄₈ | 3405 | 6 | 6 | ||
| 48. | Greenock, | 2671 | 0 | 9 | 137 | 13 | 8 | 7 | 10 | 6 | 2525 | 16 | 7 | ||||
| 49. | Grangemouth, | 1251 | 12 | 5 | 62 | 11 | 6 | 2 | 16 | 10 | 1186 | 4 | 1 | ||||
| 50. | Gainsborough, | 5 | 19 | 8 | 0 | 6 | 9 | ... | 5 | 12 | 11 | ||||||
| 51. | Gloucester, | 61 | 12 | 11 | ²⁄₈ | 3 | 1 | 8 | ²⁄₈ | 0 | 2 | 0 | 58 | 9 | 3 | ||
| 52. | Goole, | 31 | 2 | 4 | 1 | 12 | 2 | ... | 29 | 10 | 2 | ||||||
| 53. | Grimsby, | 64 | 11 | 3 | ⁴⁄₈ | 3 | 4 | 7 | ... | 61 | 6 | 8 | ⁴⁄₈ | ||||
| 54. | Gweek, | ... | ... | ... | ... | ||||||||||||
| 55. | Galway, | 38 | 6 | 0 | 1 | 18 | 3 | ⁴⁄₈ | 0 | 6 | 0 | 36 | 1 | 8 | ⁴⁄₈ | ||
| 56. | Hartlepool, | 153 | 4 | 0 | 7 | 13 | 2 | ... | 145 | 10 | 10 | ||||||
| 57. | Harwich, | ... | ... | ... | ... | ||||||||||||
| 58. | Hull, | 1532 | 8 | 2 | ⁴⁄₈ | 76 | 12 | 5 | ⁴⁄₈ | 0 | 10 | 0 | 1455 | 5 | 9 | ||
| 59. | Inverness, | 920 | 17 | 1 | ²⁄₈ | 56 | 12 | 11 | ⁴⁄₈ | 7 | 1 | 11 | 857 | 2 | 2 | ⁶⁄₈ | |
| 60. | Irvine, | 915 | 10 | 10 | 63 | 8 | 11 | 3 | 8 | 8 | 848 | 13 | 3 | ||||
| 61. | Ipswich, | 17 | 5 | 0 | 0 | 17 | 3 | 0 | 2 | 0 | 16 | 5 | 9 | ||||
| 62. | Isle of Man, | 373 | 18 | 9 | ¹⁄₈ | 22 | 15 | 5 | ⁶⁄₈ | 1 | 13 | 9 | 349 | 9 | 6 | ³⁄₄ | |
| 63. | Kirkcaldy, | 745 | 5 | 5 | 42 | 16 | 2 | 1 | 16 | 2 | 700 | 13 | 1 | ||||
| 64. | Kirkwall, | 131 | 15 | 6 | ⁴⁄₈ | 7 | 9 | 0 | ⁴⁄₈ | 0 | 9 | 9 | 123 | 16 | 9 | ||
| 65. | Leith, | 3224 | 7 | 3 | 161 | 4 | 4 | 17 | 14 | 2 | 3045 | 8 | 9 | ||||
| 66. | Lerwick, | 173 | 1 | 1 | 8 | 13 | 0 | 0 | 11 | 1 | 163 | 17 | 0 | ||||
| 67. | Lancaster, | 107 | 0 | 5 | ¹⁄₈ | 6 | 3 | 6 | ⁵⁄₈ | 0 | 18 | 8 | 99 | 18 | 2 | ⁴⁄₈ | |
| 68. | Leigh, | ... | ... | ... | ... | ||||||||||||
| 69. | Liverpool, | 6780 | 19 | 5 | 342 | 8 | 9 | 9 | 13 | 11 | 6428 | 16 | 9 | ||||
| 70. | Llanelly, | 8 | 12 | 3 | 0 | 11 | 9 | ... | 8 | 0 | 6 | ||||||
| 71. | London, | 1943 | 8 | 9 | ⁶⁄₈ | 97 | 3 | 4 | ⁶⁄₈ | ... | 1846 | 5 | 5 | ||||
| 72. | Lyme, | ... | ... | ... | ... | ||||||||||||
| 73. | Lynn, | 79 | 7 | 7 | 4 | 15 | 2 | ⁴⁄₈ | 0 | 7 | 2 | 74 | 5 | 2 | ⁴⁄₈ | ||
| 74. | Limerick, | 160 | 2 | 4 | ⁴⁄₈ | 8 | 3 | 2 | ⁴⁄₈ | 0 | 5 | 0 | 151 | 14 | 2 | ||
| 75. | Londonderry, | 1058 | 2 | 4 | 53 | 6 | 6 | ... | 1004 | 15 | 10 | ||||||
| 76. | Montrose, | 357 | 13 | 2 | ²⁄₈ | 18 | 6 | 0 | ²⁄₈ | 0 | 10 | 3 | 338 | 16 | 11 | ||
| 77. | Maldon, | ... | ... | ... | ... | ||||||||||||
| 78. | Milford, | 14 | 4 | 6 | ⁴⁄₈ | 0 | 19 | 7 | ... | 13 | 4 | 11 | ⁴⁄₈ | ||||
| 79. | Maryport, | 87 | 17 | 1 | ⁴⁄₈ | 4 | 5 | 7 | 2 | 6 | 11 | ⁴⁄₈ | 81 | 4 | 7 | ||
| 80. | Newcastle-on-Tyne, | 2118 | 16 | 8 | ⁴⁄₈ | 75 | 2 | 9 | 0 | 14 | 8 | 2042 | 19 | 3 | ⁴⁄₈ | ||
| 81. | Newhaven, | 1 | 14 | 10 | 0 | 1 | 9 | ... | 1 | 13 | 1 | ||||||
| 82. | Newport, | 41 | 2 | 8 | 2 | 1 | 1 | ⁴⁄₈ | ... | 39 | 1 | 6 | ⁴⁄₈ | ||||
| 83. | Newry, | 230 | 16 | 2 | 13 | 3 | 9 | 14 | 6 | 11 | 203 | 5 | 6 | ||||
| 84. | Perth, | 275 | 14 | 3 | 14 | 13 | 6 | ⁴⁄₈ | 0 | 19 | 10 | 260 | 0 | 10 | ⁴⁄₈ | ||
| 85. | Port-Glasgow, | 496 | 8 | 6 | 24 | 16 | 3 | 0 | 15 | 7 | 470 | 16 | 8 | ||||
| 86. | Padstow, | 2 | 15 | 1 | ³⁄₈ | 0 | 2 | 8 | ³⁄₈ | 0 | 5 | 0 | 2 | 7 | 5 | ||
| 87. | Penzance, | 1 | 6 | 10 | 0 | 1 | 4 | ... | 1 | 5 | 6 | ||||||
| 88. | Plymouth, | 25 | 4 | 9 | 1 | 6 | 2 | 0 | 1 | 0 | 23 | 17 | 7 | ||||
| 89. | Poole, | 0 | 11 | 6 | 0 | 0 | 7 | ... | 0 | 10 | 11 | ||||||
| 90. | Portsmouth, | 10 | 12 | 4 | ⁴⁄₈ | 0 | 10 | 6 | ⁴⁄₈ | 0 | 4 | 9 | 9 | 17 | 1 | ||
| 91. | Preston,[429] | 562 | 1 | 11 | 41 | 14 | 10 | ... | 520 | 7 | 1 | ||||||
| 92. | Ramsgate, | ... | ... | ... | ... | ||||||||||||
| 93. | Rochester, | 1 | 15 | 1 | 0 | 1 | 10 | ... | 1 | 13 | 3 | ||||||
| 94. | Rye, | 0 | 18 | 3 | ⁴⁄₈ | 0 | 0 | 10 | ⁴⁄₈ | ... | 0 | 17 | 5 | ||||
| 95. | Ross, | 12 | 17 | 10 | 0 | 12 | 11 | 0 | 4 | 7 | 12 | 0 | 4 | ||||
| 96. | Stranraer, | 90 | 17 | 9 | 4 | 16 | 6 | 1 | 9 | 3 | 84 | 12 | 0 | ||||
| 97. | Stornoway, | 56 | 6 | 11 | ⁴⁄₈ | 2 | 16 | 2 | ⁴⁄₈ | 0 | 3 | 6 | 53 | 7 | 3 | ||
| 98. | Scarborough, | 8 | 14 | 10 | ⁴⁄₈ | 0 | 8 | 8 | ⁴⁄₈ | ... | 8 | 6 | 2 | ||||
| 99. | Seilly, | ... | ... | ... | ... | ||||||||||||
| 100. | Shoreham, | 0 | 19 | 6 | ⁷⁄₈ | 0 | 0 | 11 | ⁷⁄₈ | ... | 0 | 18 | 7 | ||||
| 101. | Southampton, | 30 | 0 | 9 | 1 | 10 | 1 | ... | 28 | 10 | 8 | ||||||
| 102. | St Ives, | 3 | 9 | 9 | ¹⁄₈ | 0 | 5 | 2 | ¹⁄₈ | 0 | 0 | 1 | 3 | 4 | 6 | ||
| 103. | Stockton, | 226 | 19 | 2 | 12 | 0 | 2 | ⁴⁄₈ | 5 | 11 | 0 | 209 | 7 | 11 | ⁴⁄₈ | ||
| 104. | Sunderland, | 908 | 14 | 9 | ⁶⁄₈ | 47 | 1 | 4 | ⁶⁄₈ | 0 | 14 | 9 | 860 | 18 | 8 | ||
| 105. | Swansea, | 28 | 4 | 9 | ⁶⁄₈ | 1 | 12 | 3 | ... | 26 | 12 | 6 | |||||
| 106. | Sligo, | 355 | 0 | 4 | 19 | 15 | 10 | ⁶⁄₈ | 0 | 10 | 4 | 334 | 14 | 1 | ⁶⁄₈ | ||
| 107. | Truro, | 0 | 11 | 0 | 0 | 0 | 9 | ... | 0 | 10 | 3 | ||||||
| 108. | Tralee, | 9 | 7 | 10 | ⁴⁄₈ | 0 | 9 | 4 | ²⁄₈ | 0 | 2 | 8 | 8 | 15 | 10 | ²⁄₈ | |
| 109. | Wick, | 356 | 17 | 9 | ⁴⁄₈ | 20 | 10 | 2 | ⁴⁄₈ | 4 | 9 | 1 | 331 | 18 | 6 | ||
| 110. | Wigton, | 83 | 9 | 5 | 5 | 5 | 5 | 1 | 12 | 11 | 76 | 11 | 1 | ||||
| 111. | Weymouth, | 0 | 15 | 10 | ²⁄₈ | 0 | 0 | 9 | ²⁄₈ | ... | 0 | 15 | 1 | ||||
| 112. | Whitby, | 31 | 5 | 10 | 1 | 11 | 4 | ... | 29 | 14 | 6 | ||||||
| 113. | Whitehaven, | 328 | 1 | 9 | 18 | 5 | 5 | ... | 309 | 16 | 4 | ||||||
| 114. | Woodbridge, | 3 | 18 | 9 | 0 | 3 | 11 | ... | 3 | 14 | 10 | ||||||
| 115. | Waterford, | 57 | 14 | 3 | ⁴⁄₈ | 2 | 17 | 10 | ⁴⁄₈ | ... | 54 | 16 | 5 | ||||
| 116. | Westport, | 41 | 0 | 6 | ⁴⁄₈ | 2 | 1 | 0 | ... | 38 | 19 | 6 | ⁴⁄₈ | ||||
| 117. | Wexford, | 32 | 19 | 2 | 1 | 12 | 11 | ⁶⁄₈ | ... | 31 | 6 | 2 | ²⁄₈ | ||||
| 118. | Yarmouth, | 49 | 5 | 6 | 2 | 9 | 5 | ... | 46 | 16 | 1 | ||||||
| £46,001 | 11 | 3 | ⁷⁄₈ | £2401 | 7 | 3 | ⁴⁄₈ | £218 | 16 | 10 | ²⁄₈ | £43,381 | 7 | 2 | ¹⁄₈ | ||
| Deduct—Amount of fractions short credited by Bank, | 0 | 0 | 1 | ¹⁄₈ | ... | ... | 0 | 0 | 1 | ¹⁄₈ | |||||||
| £46,001 | 11 | 2 | ⁶⁄₈ | £2401 | 7 | 3 | ⁴⁄₈ | £218 | 16 | 10 | ²⁄₈ | £43,381 | 7 | 1 | |||
| Gross Receipts, | £46,001 | 11 | 2 | ⁶⁄₈ | |||||||||||||
| Deduct—Commission, | £2401 | 7 | 3 | ⁴⁄₈ | |||||||||||||
| Deduct—Repayments, &c., | 218 | 16 | 10 | ²⁄₈ | |||||||||||||
| 2620 | 4 | 1 | ⁶⁄₈ | ||||||||||||||
| Nett Duties received in year to 31st December 1846, | 43,381 | 7 | 1 | ||||||||||||||
[430]
No. II.—State shewing the Gross Receipts on account of each of the Northern Lighthouses, the Number of Vessels, and amount of Tonnage passing them;—the Particular Expenses of the Lighthouses, and their Proportions of the General Expenses, embracing Commissions to, and Repayments by, the Collectors; Expenses of the Shipping Establishment, Salaries to Officers, Experiments, and other General Expenses; also the Ordinary Expenses of Beacons and Buoys, for the Year 1846.
| No. of Vessels. |
Tonnage. | LIGHTHOUSES. | Gross Receipts. |
Surplus. | Deficiency. | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coasting. | Oversea. | Coasting. | Oversea. | ||||||||||||||||||
| 15,872 | 2,664 | 1,238,057 | 294,546 | 1. | INCHKEITH, | ... | £2524 | 9 | 2 | ²⁄₈ | |||||||||||
| Particular Expense, | £583 | 5 | 10 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 577 | 15 | 9 | ²⁄₈ | |||||||||||||||||
| Total Expenditure, | 1161 | 1 | 7 | ⁶⁄₈ | |||||||||||||||||
| Balance, | £1363 | 7 | 6 | ⁴⁄₈ | |||||||||||||||||
| 20,101 | 3,349 | 1,843,210 | 383,516 | 2. | ISLE OF MAY, | £3676 | 18 | 11 | |||||||||||||
| Add for Leading Light, | 148 | 9 | 6 | ⁴⁄₈ | |||||||||||||||||
| £3825 | 8 | 5 | ⁴⁄₈ | ||||||||||||||||||
| Particular Expense, | £952 | 3 | 9 | ||||||||||||||||||
| Share of General Expense, | 941 | 8 | 6 | ||||||||||||||||||
| Total Expenditure, | 1893 | 12 | 3 | ||||||||||||||||||
| Balance, | 1931 | 16 | 2 | ⁴⁄₈ | |||||||||||||||||
| 14,610 | 4,485 | 1,299,875 | 632,328 | 3. | BELL ROCK, | ... | £5342 | 15 | 5 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £989 | 1 | 3 | ²⁄₈ | |||||||||||||||||
| Share of General Expense, | 977 | 17 | 9 | ||||||||||||||||||
| Total Expenditure, | 1966 | 19 | 0 | ²⁄₈ | |||||||||||||||||
| Balance, | 3375 | 16 | 5 | ²⁄₈ | |||||||||||||||||
| 7,915 | 3,978 | 788,947 | 587,977 | 4. | GIRDLENESS, | ... | £2458 | 4 | 5 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £548 | 18 | 1 | ||||||||||||||||||
| Share of General Expense, | 544 | 5 | 8 | ||||||||||||||||||
| Total Expenditure, | 1093 | 3 | 9 | ||||||||||||||||||
| Balance, | 1365 | 0 | 8 | ⁴⁄₈ | |||||||||||||||||
| 5,293 | 4,012 | 419,988 | 590,453 | 5. | BUCHANNESS, | ... | £1880 | 1 | 3 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £623 | 5 | 3 | ||||||||||||||||||
| Share of General Expense, | 617 | 4 | 1 | ⁶⁄₈ | |||||||||||||||||
| Total Expenditure, | 1240 | 9 | 4 | ⁶⁄₈ | |||||||||||||||||
| Balance, | 639 | 11 | 10 | ⁶⁄₈ | |||||||||||||||||
| 4,829 | 2,819 | 390,166 | 546,856 | 6. | KINNAIRDSHEAD, | ... | £1744 | 11 | 3 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £578 | 10 | 0 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 573 | 16 | 11 | ²⁄₈ | |||||||||||||||||
| Total Expenditure, | 1152 | 6 | 11 | ⁶⁄₈ | |||||||||||||||||
| Balance, | 592 | 4 | 6 | ⁶⁄₈ | |||||||||||||||||
| 2,256 | 273 | 191,345 | 18,282 | 7. | TARBETNESS, | ... | £329 | 17 | 4 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £574 | 11 | 11 | ||||||||||||||||||
| Share of General Expense, | 569 | 18 | 1 | ²⁄₈ | |||||||||||||||||
| Total Expenditure, | 1144 | 10 | 0 | ²⁄₈ | |||||||||||||||||
| Balance, | ... | £814 | 12 | 7 | ⁴⁄₈ | ||||||||||||||||
| 279 | 644 | 32,149 | 113,598 | 8. | SUMBURGHHEAD, | ... | £286 | 18 | 2 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £597 | 5 | 3 | ⁶⁄₈ | |||||||||||||||||
| Share of General Expense, | 591 | 11 | 8 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 1188 | 17 | 0 | ²⁄₈ | |||||||||||||||||
| Balance, | ... | £901 | 18 | 9 | ⁴⁄₈ | ||||||||||||||||
| 307 | 2,326 | 33,710 | 528,647 | 9. | STARTPOINT, | ... | £1154 | 5 | 4 | ²⁄₈ | |||||||||||
| Particular Expense, | £347 | 0 | 8 | ||||||||||||||||||
| Share of General Expense, | 345 | 4 | 4 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 692 | 5 | 0 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 462 | 0 | 3 | ⁶⁄₈ | |||||||||||||||||
| 2,434 | 2,430 | 181,284 | 525,582 | 10. | PENTLAND SKERRIES, | ... | £1370 | 10 | 5 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £851 | 8 | 11 | ||||||||||||||||||
| Share of General Expense, | 841 | 17 | 10 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 1693 | 6 | 9 | ⁴⁄₈ | |||||||||||||||||
| Balance, | ... | 322 | 16 | 3 | ⁶⁄₈ | ||||||||||||||||
| 1,911 | 2,267 | 139,379 | 524,685 | 11. | DUNNETHEAD,[431] | ... | £1311 | 1 | 10 | ²⁄₈ | |||||||||||
| Particular Expense, | £470 | 19 | 7 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 467 | 8 | 4 | ||||||||||||||||||
| Total Expenditure, | 938 | 7 | 11 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 372 | 13 | 10 | ⁶⁄₈ | |||||||||||||||||
| 1,700 | 2,231 | 131,138 | 517,333 | 12. | CAPEWRATH, | ... | £1278 | 9 | 9 | ||||||||||||
| Particular Expense, | £587 | 6 | 11 | ²⁄₈ | |||||||||||||||||
| Share of General Expense, | 581 | 14 | 7 | ²⁄₈ | |||||||||||||||||
| Total Expenditure, | 1169 | 1 | 6 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 109 | 8 | 2 | ⁴⁄₈ | |||||||||||||||||
| 1,734 | 1,153 | 137,060 | 226,941 | 13. | ISLAND GLASS, | ... | £679 | 1 | 10 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £515 | 2 | 10 | ²⁄₈ | |||||||||||||||||
| Share of General Expense, | 510 | 15 | 6 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 1025 | 18 | 4 | ⁶⁄₈ | |||||||||||||||||
| Balance, | ... | 346 | 16 | 6 | |||||||||||||||||
| 669 | 1,821 | 9,517 | 466,010 | 14. | BARRAHEAD, | ... | £1063 | 3 | 2 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £594 | 3 | 10 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 588 | 12 | 7 | ||||||||||||||||||
| Total Expenditure, | 1182 | 16 | 5 | ⁴⁄₈ | |||||||||||||||||
| Balance, | ... | 119 | 13 | 2 | ⁶⁄₈ | ||||||||||||||||
| 555 | 1,788 | 52,541 | 461,313 | 15. | SKERRYVORE, | ... | £2090 | 11 | 3 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £1122 | 0 | 7 | ||||||||||||||||||
| Share of General Expense, | 1108 | 19 | 1 | ||||||||||||||||||
| Total Expenditure, | 2239 | 19 | 8 | ||||||||||||||||||
| Balance, | ... | 140 | 8 | 4 | ⁴⁄₈ | ||||||||||||||||
| 2,430 | 34 | 159,719 | 4,436 | 16. | LISMORE, | ... | £239 | 11 | 4 | ||||||||||||
| Particular Expense, | £515 | 14 | 2 | ²⁄₈ | |||||||||||||||||
| Share of General Expense, | 511 | 15 | 4 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 1027 | 9 | 6 | ⁶⁄₈ | |||||||||||||||||
| Balance, | ... | 787 | 18 | 2 | ⁶⁄₈ | ||||||||||||||||
| 3,152 | 1,550 | 385,786 | 382,841 | 17. | RHINNS OF ISLAY, | ... | £1414 | 5 | 8 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £569 | 12 | 7 | ⁶⁄₈ | |||||||||||||||||
| Share of General Expense, | 564 | 19 | 6 | ⁶⁄₈ | |||||||||||||||||
| Total Expenditure, | 1134 | 12 | 2 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 279 | 13 | 6 | ²⁄₈ | |||||||||||||||||
| 5,023 | 1,440 | 509,914 | 357,682 | 18. | MULL OF KINTYRE, | ... | £1549 | 0 | 1 | ||||||||||||
| Particular Expense, | £554 | 17 | 10 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 550 | 3 | 10 | ⁶⁄₈ | |||||||||||||||||
| Total Expenditure, | 1105 | 1 | 9 | ²⁄₈ | |||||||||||||||||
| Balance, | 443 | 18 | 3 | ⁶⁄₈ | |||||||||||||||||
| 12,372 | 1,937 | 1,403,359 | 450,849 | 19. | PLADDA, | ... | £2762 | 14 | 3 | ⁷⁄₈ | |||||||||||
| Particular Expense, | £584 | 10 | 10 | ||||||||||||||||||
| Share of General Expense, | 579 | 15 | 2 | ²⁄₈ | |||||||||||||||||
| Total Expenditure, | 1164 | 6 | 0 | ²⁄₈ | |||||||||||||||||
| Balance, | 1598 | 8 | 3 | ⁵⁄₈ | |||||||||||||||||
| 12,453 | 2,776 | 1,407,921 | 645,447 | 20. | CORSEWALL, | ... | £2811 | 5 | 3 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £465 | 13 | 4 | ||||||||||||||||||
| Share of General Expense, | 462 | 9 | 9 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 928 | 3 | 1 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 1883 | 2 | 2 | ²⁄₈ | |||||||||||||||||
| 12,884 | 2,458 | 1,648,915 | 531,056 | 21. | MULL OF GALLOWAY, | ... | £2823 | 19 | 8 | ⁶⁄₈ | |||||||||||
| Particular Expense, | £517 | 0 | 5 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 512 | 14 | 11 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 1029 | 15 | 5 | ||||||||||||||||||
| Balance, | 1794 | 4 | 3 | ⁶⁄₈ | |||||||||||||||||
| 9,195 | 98 | 729,918 | 17,431 | 22. | LITTLE ROSS, | ... | £1187 | 7 | 9 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £516 | 18 | 6 | ²⁄₈ | |||||||||||||||||
| Share of General Expense, | 512 | 14 | 11 | ²⁄₈ | |||||||||||||||||
| Total Expenditure, | 1029 | 13 | 5 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 157 | 14 | 4 | ||||||||||||||||||
| 9,733 | 1,034 | 843,235 | 209,237 | 23. | POINT OF AYRE, | ... | £1755 | 17 | 5 | ⁴⁄₈ | |||||||||||
| Particular Expense, | £409 | 1 | 4 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 406 | 6 | 4 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 815 | 7 | 9 | ||||||||||||||||||
| Balance, | 940 | 9 | 8 | ⁴⁄₈ | |||||||||||||||||
| 13,867 | 2,559 | 1,769,475 | 546,244 | 24. | CALF OF MAN (2 Lights), | ... | £3839 | 2 | 11 | ²⁄₈ | |||||||||||
| Particular Expense, | £813 | 19 | 5 | ||||||||||||||||||
| Share of General Expense, | 805 | 8 | 7 | ⁴⁄₈ | |||||||||||||||||
| Total Expenditure, | 1619 | 8 | 0 | ⁴⁄₈ | |||||||||||||||||
| Balance, | 2219 | 14 | 10 | ⁶⁄₈ | |||||||||||||||||
| 1,592 | 198 | 130,026 | 14,288 | 25. | COVESEA SKERRIES,*[432] | ... | £193 | 7 | 0 | ||||||||||||
| Particular Expense, | £419 | 16 | 8 | ⁴⁄₈ | |||||||||||||||||
| Share of General Expense, | 417 | 3 | 1 | ⁶⁄₈ | |||||||||||||||||
| Total Expenditure, | 836 | 19 | 10 | ²⁄₈ | |||||||||||||||||
| Balance, | ... | 643 | 12 | 10 | ²⁄₈ | ||||||||||||||||
| 26. | CROMARTY,* | ... | £27 | 14 | 11 | ||||||||||||||||
| Particular Expense, | £339 | 17 | 3 | ||||||||||||||||||
| Share of General Expense, | 338 | 6 | 4 | ⁶⁄₈ | |||||||||||||||||
| Total Expenditure, | 678 | 3 | 7 | ⁶⁄₈ | |||||||||||||||||
| Balance, | ... | 650 | 8 | 8 | ⁶⁄₈ | ||||||||||||||||
| 27. | CHANONRY,* | ... | £57 | 15 | 1 | ||||||||||||||||
| Particular Expense, | £284 | 7 | 1 | ||||||||||||||||||
| Share of General Expense, | 283 | 2 | 8 | ⁶⁄₈ | |||||||||||||||||
| Total Expenditure, | 567 | 9 | 9 | ⁴⁄₈ | |||||||||||||||||
| Balance, | ... | 509 | 14 | 8 | ⁴⁄₈ | ||||||||||||||||
| 28. | LOCH RYAN,* | ... | |||||||||||||||||||
| Particular Expense, | £176 | 5 | 7 | ||||||||||||||||||
| Share of General Expense, | 176 | 14 | 1 | ||||||||||||||||||
| Total Expenditure, | ... | ... | 352 | 19 | 8 | ||||||||||||||||
| * | Note.—Covesea Skerries, Cromarty, and Chanonry, were not lighted till the 15th May, to which is owing the small amount of their Revenue; and Loch Ryan was not lighted till the 3d of March subsequent to the period embraced in this State. | ||||||||||||||||||||
| 163,166 | 50,324 | 15,926,634 | 9,577,478 | Total, | ... | ... | £19,529 | 5 | 1 | ¹⁄₈ | £5591 | 0 | 0 | ²⁄₈ | |||||||
| RECONCILEMENT. | |||||||||||||||||||||
| The Surplus amounts as above to | £19,529 | 5 | 1 | ¹⁄₈ | |||||||||||||||||
| And the Deficiency to | 5,591 | 0 | 0 | ²⁄₈ | |||||||||||||||||
| Actual Surplus, | £13,938 | 5 | 0 | ⁷⁄₈ | |||||||||||||||||
| Deduct—Fractions short—credited by Bank, &c., | 0 | 0 | 1 | ¹⁄₈ | |||||||||||||||||
| Surplus, as per p. 415, | £13,938 | 4 | 11 | ⁶⁄₈ | |||||||||||||||||
| Add—The Receipts derived from other sources besides Light-duties, per p. 419, | 1,893 | 17 | 6 | ||||||||||||||||||
| £15,832 | 2 | 5 | ⁶⁄₈ | ||||||||||||||||||
| But there has been expended, besides the amount allocated to the different Lighthouses above, as per p. 425, | 28,311 | 9 | 6 | ²⁄₈ | |||||||||||||||||
| Amount superexpended, per p. 425, | £12,479 | 7 | 0 | ⁴⁄₈ | |||||||||||||||||
Note.—The General Expenses in the above State are allocated to each Lighthouse in the same proportions as the Particular Expenses. The expense of Beacons and Buoys is equally divided by the number of Lighthouses, and the same amount allocated to each Lighthouse.
[433]
No. III.—Statement shewing the Increase in Tonnage during the Years 1843-44-45-46, over 1842.
| Coasting. | Oversea. | Total. | ||||
|---|---|---|---|---|---|---|
| The amount of the Tonnage in 1842 was | 11,620,172 | 6,738,433 | 18,358,605 | |||
| The amount of the Tonnage in 1843 was | 12,190,745 | 7,194,932 | 19,385,677 | |||
| Increase in 1843 over 1842 | 570,573 | 456,499 | 1,027,072 | |||
| Coasting. | Oversea. | Total. | ||||
| The amount of Tonnage in 1843 was | 12,190,745 | 7,194,932 | 19,385,677 | |||
| The amount of Tonnage in 1844 was | 13,425,614 | 7,737,617 | 21,163,231 | |||
| Increase in 1844 over 1843 | 1,234,869 | 542,685 | 1,777,554 | |||
| Increase in 1844 over 1842 | 1,805,442 | 999,184 | 2,804,626 | |||
| Coasting. | Oversea. | Total. | ||||
| The amount of Tonnage in 1844 was | 13,425,614 | 7,737,617 | 21,163,231 | |||
| The amount of Tonnage in 1845 was | 15,566,461 | 9,300,983 | 24,867,444 | |||
| Increase in 1845 over 1844 | 2,140,847 | 1,563,366 | 3,704,213 | |||
| Increase in 1845 over 1842 | 3,946,289 | 2,562,550 | 6,508,839 | |||
| Coasting. | Oversea. | Total. | ||||
| The amount of Tonnage in 1845 was | 15,566,461 | 9,300,983 | 24,867,444 | |||
| The amount of Tonnage in 1846 was | 15,926,634 | 9,577,478 | 25,504,112 | |||
| Increase in 1846 over 1845 | 360,173 | 276,495 | 636,668 | |||
| Increase in 1846 over 1842 | 4,306,462 | 2,839,045 | 7,145,507 | |||
[434]
1. The Lamps shall be kept burning bright and clear every night from sunset to sunrise; and in order that the greatest degree of light may be maintained throughout the night, the Wicks must be trimmed every four hours, or oftener if necessary; and the Keeper who has the first watch shall take care to turn the oil-valves so as to let the oil flow into the Burner a sufficient time before lighting.
2. The Light-keepers shall keep a regular and constant Watch in the Light-room throughout the night. The First Watch shall begin at sunset. The Light-keepers are to take the watches alternately, in such manner that he who has the first watch one night, shall have the second watch next night. The length or duration of the watch shall not, in ordinary cases, exceed four hours; but during the period between the months of October and March, both inclusive, the first watch shall change at eight o’clock. The watches shall at all times be so arranged as to have a shift at midnight.
3. At stations where there is only one Light-room, the daily duty shall be laid out in two departments, and the Light-keepers shall change from one department to the other every Saturday night.
4. First Department.—The Light-keeper who has this department, shall immediately after the morning Watch, polish or otherwise cleanse the Reflectors or Refractors till they are brought into a proper state of brilliancy; he shall also thoroughly cleanse the lamps, and carefully dust the Chandelier. He shall supply the Burners with cotton, the Lamps with oil, and shall have every thing connected with the Apparatus in a state of readiness for lighting in the evening.
5. Second Department.—The Light-keeper who has this department shall cleanse the glass of the Lantern, lamp-glasses, copper and brass work and utensils, the walls, floors, and balcony of the Light-room, and the apparatus and machinery therewith connected; together with the Tower stair, passage, doors, and windows, from the Light-room to the Oil cellar.
[435]
6. For the more effectual cleansing of the glass of the Lantern, and management of the Lamps at the time of lighting, both Light-keepers shall be upon watch throughout the first hour of the first watch every night, during the winter period, between the first day of October and last day of March, when they shall jointly do the duty of the Light-room during that hour. These changes to and from the double watch shall be intimated by the Keepers in the Monthly Returns for October and April.
7. At those stations where there are two Light-rooms, each Light-keeper shall perform the entire duty of both departments in that Light-room to which he may be especially appointed. But after the first hour of the first Watch, the Light-keeper who has charge of this watch shall perform the whole duty of trimming and attending the Lights of both Light-rooms till the expiry of his watch; and in like manner, his successor on the watch shall perform the whole duty of both Light-rooms during his watch.
8. The Light-keeper on duty shall on no pretence whatever, during his watch, leave the Light-room and balcony, or the passage leading from one Light-room to another, at stations where there are two Lights. Bells are provided at each Light-room to enable the Light-keeper on duty to summon the absent Light-keeper; and if at any time the Light-keeper on duty shall think the presence or assistance of the Light-keeper not on duty is necessary, he shall call him by ringing his bell, which should be immediately answered by the return signal, and the Keeper so called, should repair to the Light-room without delay. In like manner, when the watches come to be changed, the bell shall be rung to call the Light-keeper next in turn. After which the Light-keeper on duty shall, at his peril, remain on guard till he is relieved by the Light-keeper in person who has the next watch.
9. Should the bell of the Light-keeper whose turn it is to mount guard, happen to be in an unserviceable state, the other house-bell shall be used, and some of the inmates of that house shall call the Light-keeper not on duty, so as by all means to avoid leaving the Light-room without a constant watch during the night.
10. The Principal Light-keeper is held responsible for the safety and good order of the Stores, Utensils, and apparatus of what kind soever, and for every thing being put to its proper use, and kept in its proper place. He shall take care that none of the stores or materials are wasted, and shall observe the strictest economy, and the most careful management, yet so as to maintain in every respect the best possible light.
11. The Principal Light-keeper shall daily serve out the allowance of[436] Oil and other Stores for the use of the Light-room. The oil is to be measured by the Assistant, at the sight of the Principal Light-keeper.
12. The Light-keepers shall keep a daily Journal of the quantity of Oil expended, the routine of their duty, and the state of the Weather, embodying any other remarks that may occur. These shall be written in the Journal-Books to be kept at each station for the purpose, at the periods of the day when they occur, as they must on no account be trusted to memory. On the first day of each month they shall make up and transmit to the Engineer a return, which shall be an accurate copy of the Journal for the preceding month.
13. The Light-keepers are also required to take notice of any Shipwreck which shall happen within the district of the Lighthouse, and to enter an account thereof, according to the prescribed form, in a Book furnished to each Station for this purpose; and in such account he shall state whether the Light was seen by any one on board the shipwrecked Vessel and recognised by them, and how long it was seen before the vessel struck. A copy of this entry shall form the Shipwreck Return, to be forthwith forwarded to the Engineer.
14. A book containing a Note of the Vessels passing each Lighthouse daily shall be kept; and an annual Schedule, shewing the number of vessels in each month, shall be sent to the Engineer in the month of January.
15. The Monthly and Shipwreck Returns are to be written by the Assistant, and the accompanying letters by the Principal Light-keeper. The whole shall be carefully compared and signed by both Light-keepers, as directed by the printed form, and despatched by post to the Engineer as soon as possible.
16. For the purpose of keeping up the practical knowledge of the “Occasional Keeper,” he shall be annually called in by the Principal Light-keeper to do duty for a fortnight in the month of January; and the same shall be stated in the Monthly Letter.
17. The Principal Light-keeper is held responsible for the regularity of the Watches throughout the night, for the cleanliness and good order of the Reflecting or Refracting Apparatus, Machinery, and Utensils, and for the due performance of the whole duty of the Light-room or Light-rooms, as the case may be, whether performed by him personally, or by the Assistant.
18. The Principal Light-keeper is also held responsible for the good order and condition of the Household Furniture belonging to the Lighthouse Board, as well in his own as in the Assistant’s house. This duty extends[437] also to the cleanliness of the several apartments, passages, stairs, roofs, water-cisterns, store-rooms, work-shops, privies, ash-pits of the dwelling-houses, offices, court, and immediate access to the Lighthouse.
19. The Light-keepers shall endeavour to keep in good order and repair the Dykes enclosing the Lighthouse grounds, the Landing-places, and Roads leading from thence to the Lighthouse and the Drains therewith connected, together with all other things placed under their charge.
20. When stores of any kind are to be landed for the use of the Lighthouse, the Light-keepers shall attend and give their assistance. The Principal Light-keeper must, upon these occasions, satisfy himself, as far as possible, of the quantity and condition of the stores received, which must be duly entered in the Store-book and Monthly Return-book.
21. The Light-keepers are to make a Report of the quality of the Stores, in the Monthly Return for March annually, or earlier should circumstances render this necessary; and this Report must proceed upon special trial of the several Cisterns of Oil and of the other Stores in detail, both at the time of receiving them and after the experience of the winter months.
22. At all stations where Peat Fuel is in use, there must be such a quantity of Peats provided, that the Stock of the former year shall be a sufficient supply to the end of the current year.
23. Should the supply of any of the Lighthouse Stores at any time appear to the Principal Light-keeper to be getting short, so as thereby to endanger the regular appearance of the Light, he shall immediately intimate the same to the Engineer, and he must be guided by prudence in reducing the stated number of Burners until a supply be received.
24. The Light-keepers are prohibited from carrying on any trade or business whatever. They are also prohibited from having any boarders or lodgers in their dwelling-houses, and from keeping dogs at the Lighthouse establishments.
25. The Light-keepers are also directed to take care that no smuggled goods are harboured or concealed in any way in or about the Lighthouse premises or grounds.
26. The Light-keepers have permission to go from home to draw their salaries, and also to attend church. The Assistant Light-keeper, on all occasions of leave of absence, must consult the Principal Light-keeper as to the proper time for such leave, and obtain his consent; in like manner, the Principal Light-keeper shall duly intimate his intention of going from home[438] to the Assistant Light-keeper;—it being expressly ordered that only one Light-keeper shall be absent from the Lighthouse at one and the same time.
27. While the Principal Light-keeper is absent, or is incapacitated for duty by sickness, the full charge of the Light-room duty and of the premises shall devolve upon the Assistant, who shall in that case have access to the keys of the Light-room stores, and be held responsible in all respects as the Principal Light-keeper; and in the case of the incapacity of either Light-keeper, the assistance of the Occasional Light-keeper shall be immediately called in, and notice of the same given to the Engineer. Notice of any such occurrences to be taken in the Monthly Return, or by special letter to the Engineer, should circumstances render this necessary.
28. The Light-keepers are required to be sober and industrious, cleanly in their persons and linens, and orderly in their families. They must conduct themselves with civility to strangers, by shewing the premises, at such hours as do not interfere with the proper duties of their office; it being expressly understood, that strangers shall not be admitted into the Light-room after sunset. But no money or other gratuity shall be taken from strangers on any pretence whatever.
29. The Light-keepers are to appear in their Uniform-dress when any of the Commissioners or Principal Officers visit a station, and also on Sunday;—on which day, at noon, the weather permitting, the Lighthouse flag shall be hoisted by the Assistant Light-keeper, or in his absence by the Principal Light-keeper, when it shall remain displayed until sunset.
30. These Instructions are to be read in the Light-room by the Principal Light-keeper, in the hearing of his Assistant, on the term days, before drawing his salary; and notice thereof taken in the Monthly Returns.
31. In the event of any neglect occurring in the performance of any part of the duties required from a Light-keeper, the offending party shall, jointly with the other Light-keeper or Light-keepers at the station, send immediate notice of the circumstance to the Engineer; and in the event of one party refusing or neglecting to concur in giving this intimation, the others (whether Principals or Assistants) shall proceed to give the notice in their own names.
32. The breach of any of the foregoing Rules and Instructions shall subject the Light-keepers to dismissal, or to such other punishment as the nature of the offence may require.
33. It is recommended that the Principal Light-keeper, or other Principal[439] Officer at the respective Lighthouses for the time being, shall, every Sunday, perform the service pointed out for the inmates, by reading a portion of the Scriptures, and any other religious book furnished by the Board, and the Prayer composed for their use by the Rev. Dr Brunton, one of the Ministers of Edinburgh, or other Prayers in any work furnished by the Board. For this purpose, the Principal Light-keeper shall invite the families to assemble at noon in the Visiting Officer’s room.
34. The Light-keepers are to observe that the above general Regulations are without prejudice to any more special Instructions which may be made applicable to any particular Lighthouse, or to such orders as may from time to time be issued by the Engineer.
Alan Stevenson, Engineer
for Northern Lighthouses.
Northern Lights Office, Edinburgh,
16th June 1847.
Edinburgh, 16th June 1847.
The Commissioners having considered the preceding Rules and Instructions, approve of the same, direct them to be substituted for those now in use, appoint them to be signed by the Engineer, and copies of them and of this Minute to be issued to the present Light-keepers; direct a copy to be delivered in future to each Light-keeper at the time of his appointment, that they may understand that they are placed under the department and superintendence of the Engineer, who is held responsible for the strict observance of the Rules and Instructions, and for their general good conduct; that the Engineer has power, in case of neglect or disobedience, instantly to suspend and remove any of the Light-keepers, and to report the case to the Commissioners, by whom it will be considered, and the offending party subjected to dismissal, or such other punishment as the offence may merit. In case of a punishment less than dismissal, that circumstance, as well as the general conduct of the Light-keeper, will always be taken into consideration when any application may be made for superannuated allowance.
Extracted from the Minutes by
Alex. Cuningham, Sec.
[440]
EDINBURGH:
PRINTED BY NEILL AND COMPANY, OLD FISHMARKET.
PLATE I
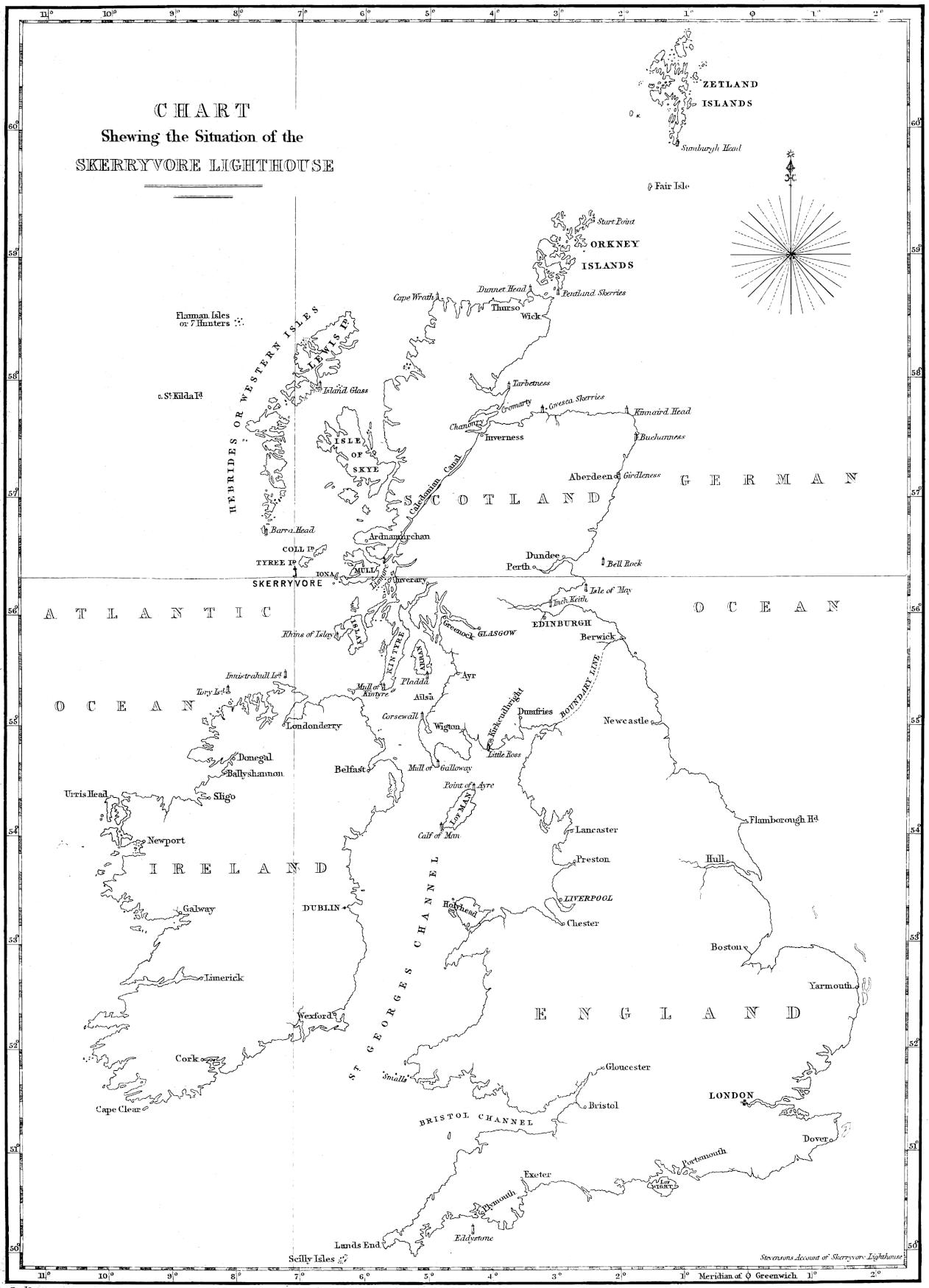
Engd. by W. & A. K. Johnston Edinr.
CHART
Shewing the Situation of the
SKERRYVORE LIGHTHOUSE
Stevensons Account of Skerryvore Lighthouse
PLATE II.
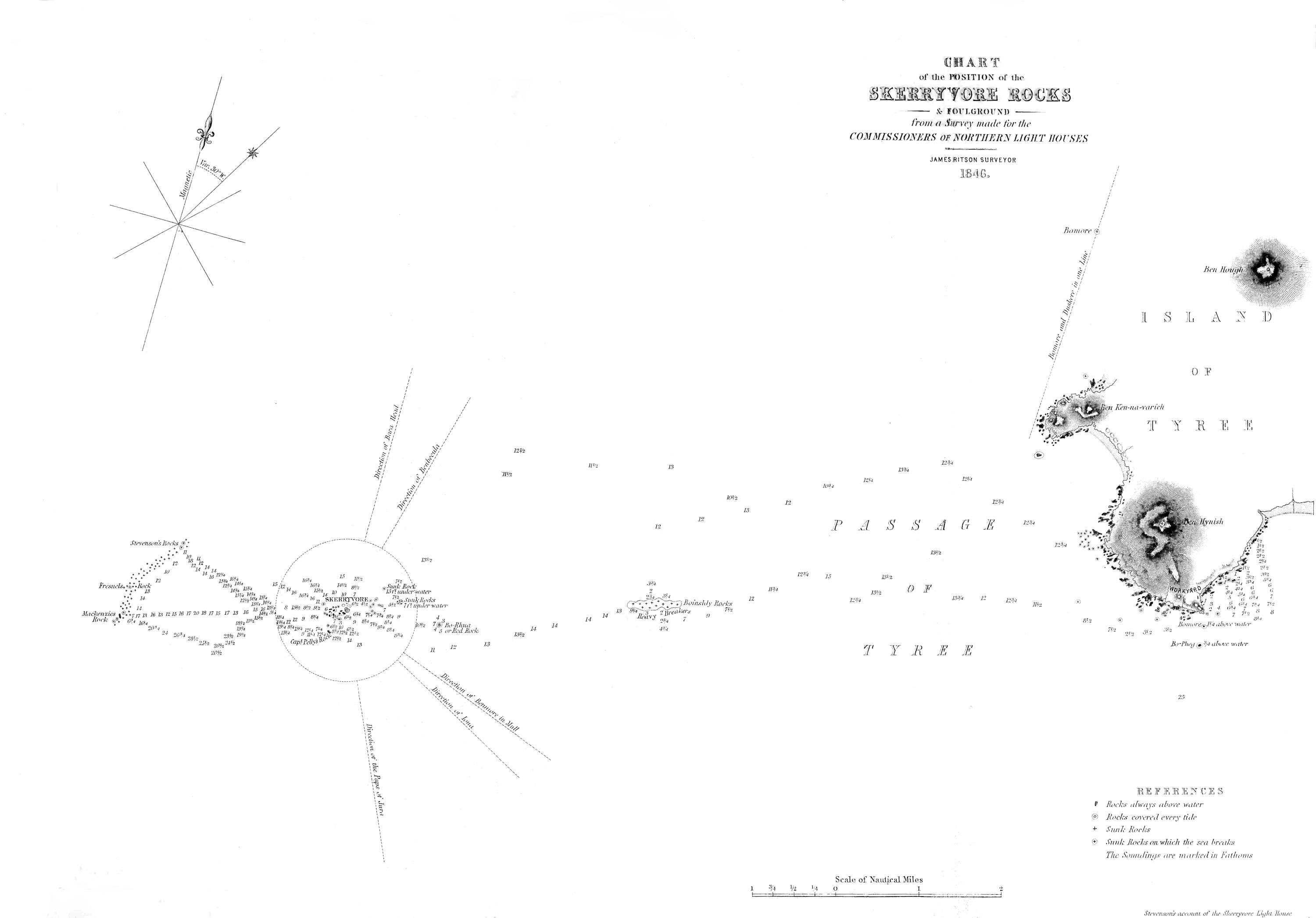
Engraved by W. & A. K. Johnston Edinburgh.
CHART
of the POSITION of the
SKERRYVORE ROCKS
& FOULGROUND
from a Survey made for the
COMMISSIONERS OF NORTHERN LIGHT HOUSES
JAMES RITSON SURVEYOR
1846.
Stevenson’s Account of the Skerryvore Lighthouse.
PLATE
Stevenson’s Account of Skerryvore Lighthouse.
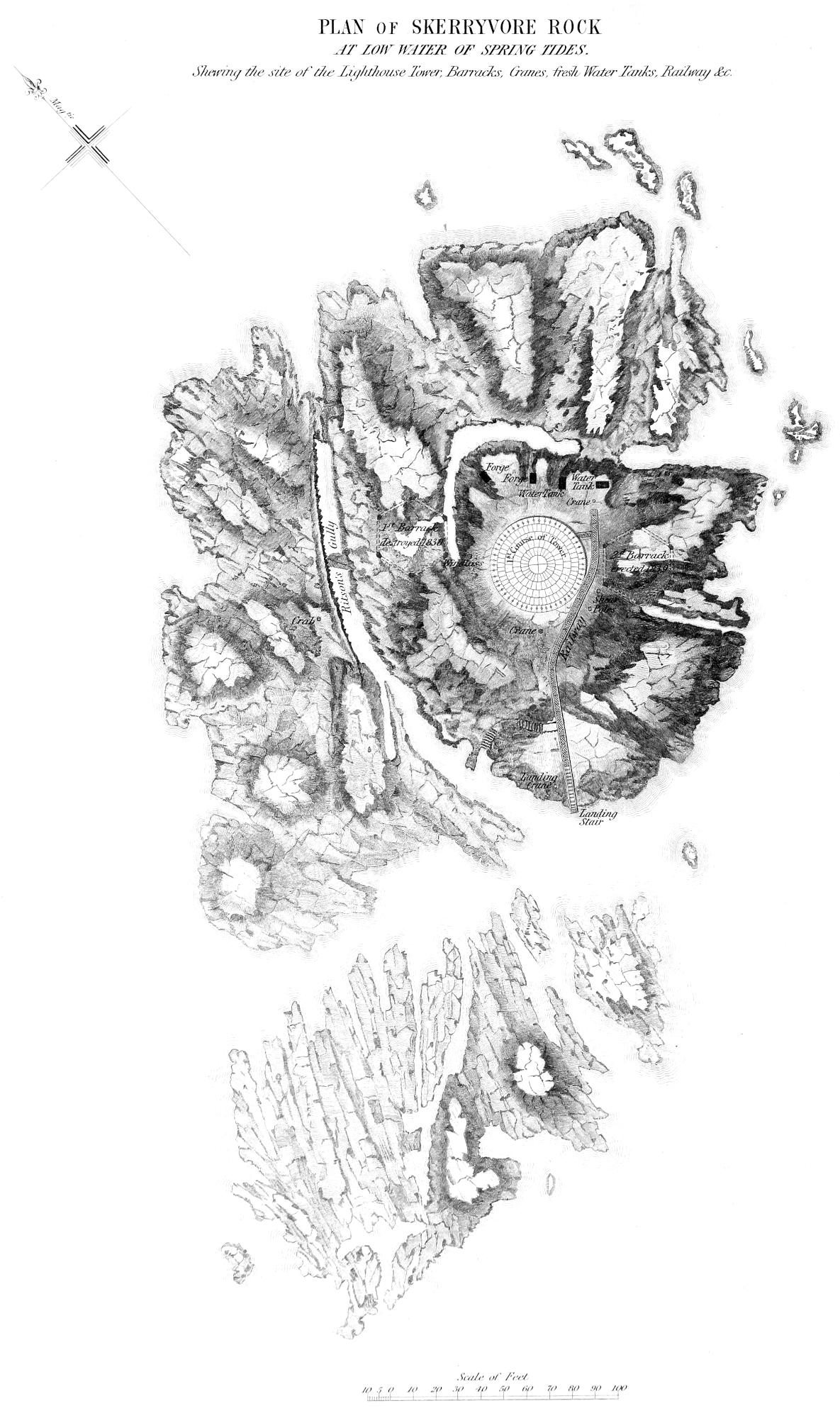
James Andrews, Delt. William Miller, Sculpt.
PLAN of SKERRYVORE ROCK
AT LOW WATER OF SPRING TIDES.
Shewing the site of the Lighthouse Tower, Barracks, Cranes, fresh Water Tanks, Railway &c.
No. III.
Stevenson’s Account of Skerryvore Lighthouse.
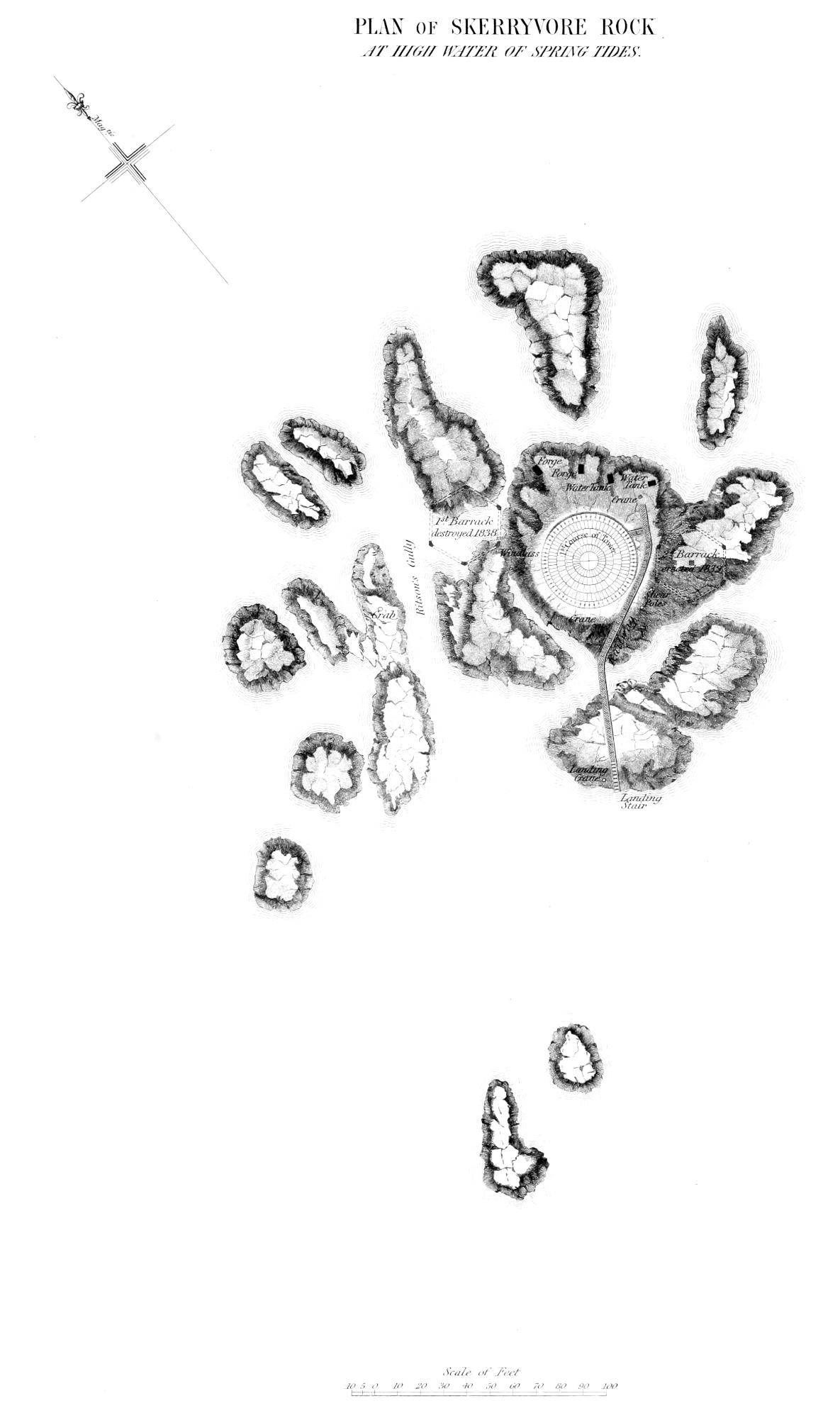
James Andrews, Delt. William Miller, Sculpt.
PLAN of SKERRYVORE ROCK
AT HIGH WATER OF SPRING TIDES.
PLATE IV.
Stevenson’s Account of Skerryvore Lighthouse.
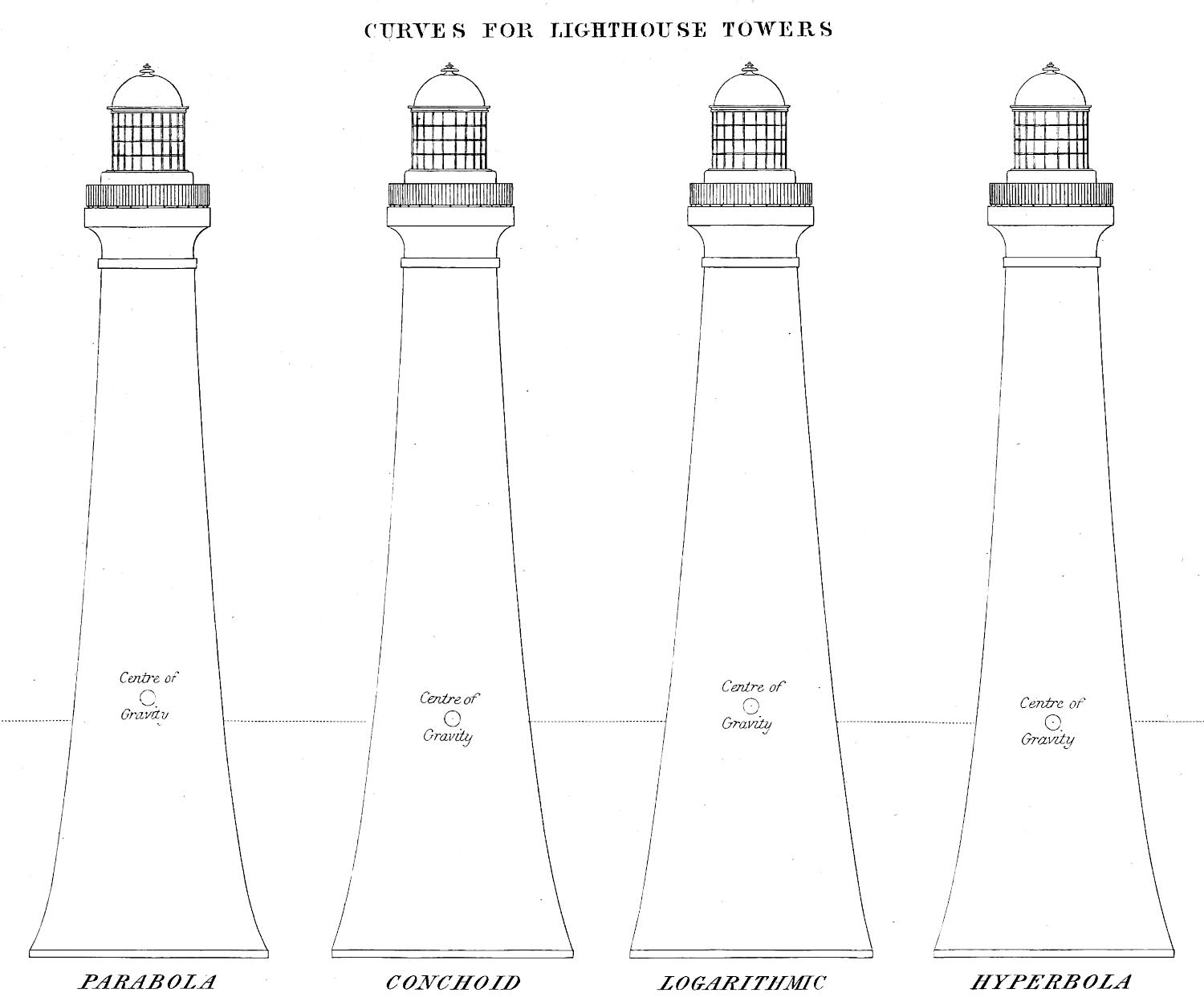
James Andrews, Delt. G. Aikman Sc
CURVES FOR LIGHTHOUSE TOWERS
PARABOLA CONCHOID LOGARITHMIC HYPERBOLA

W. & A. K. Johnston Sculpt.
MARINE DYNAMOMETER, SMALL SIZE, LENGTH 18 INCHES.
PLATE V.
Stevenson’s Account of Skerryvore Lighthouse.
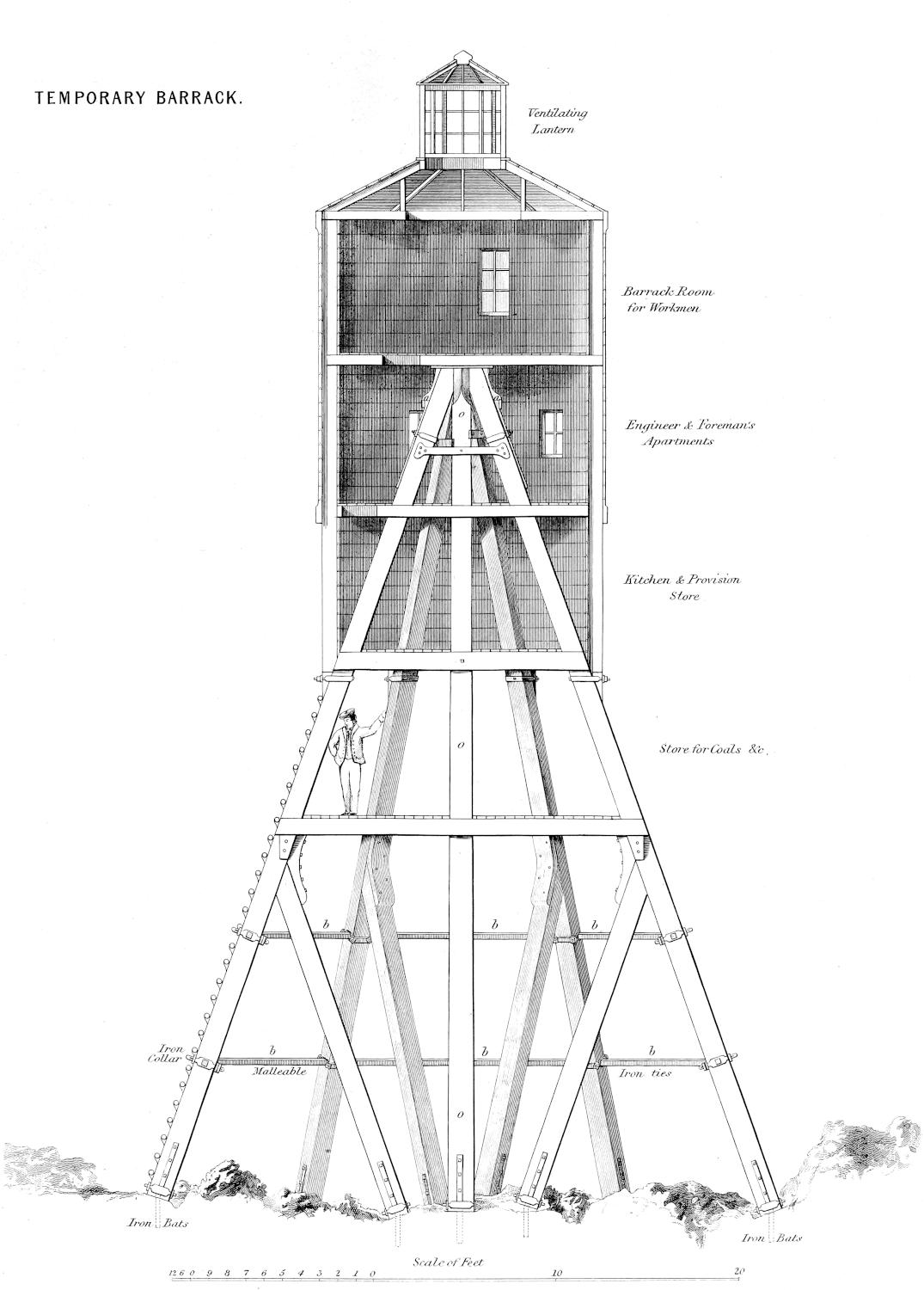
Walter Ferrier Delt. G. Aikman Sculpt.
TEMPORARY BARRACK.
Barrack Room for Workmen
Engineer & Foreman’s Apartments
Kitchen & Provision Store
Store for Coals &c.
PLATE VI.
Stevenson’s Account of Skerryvore Lighthouse.
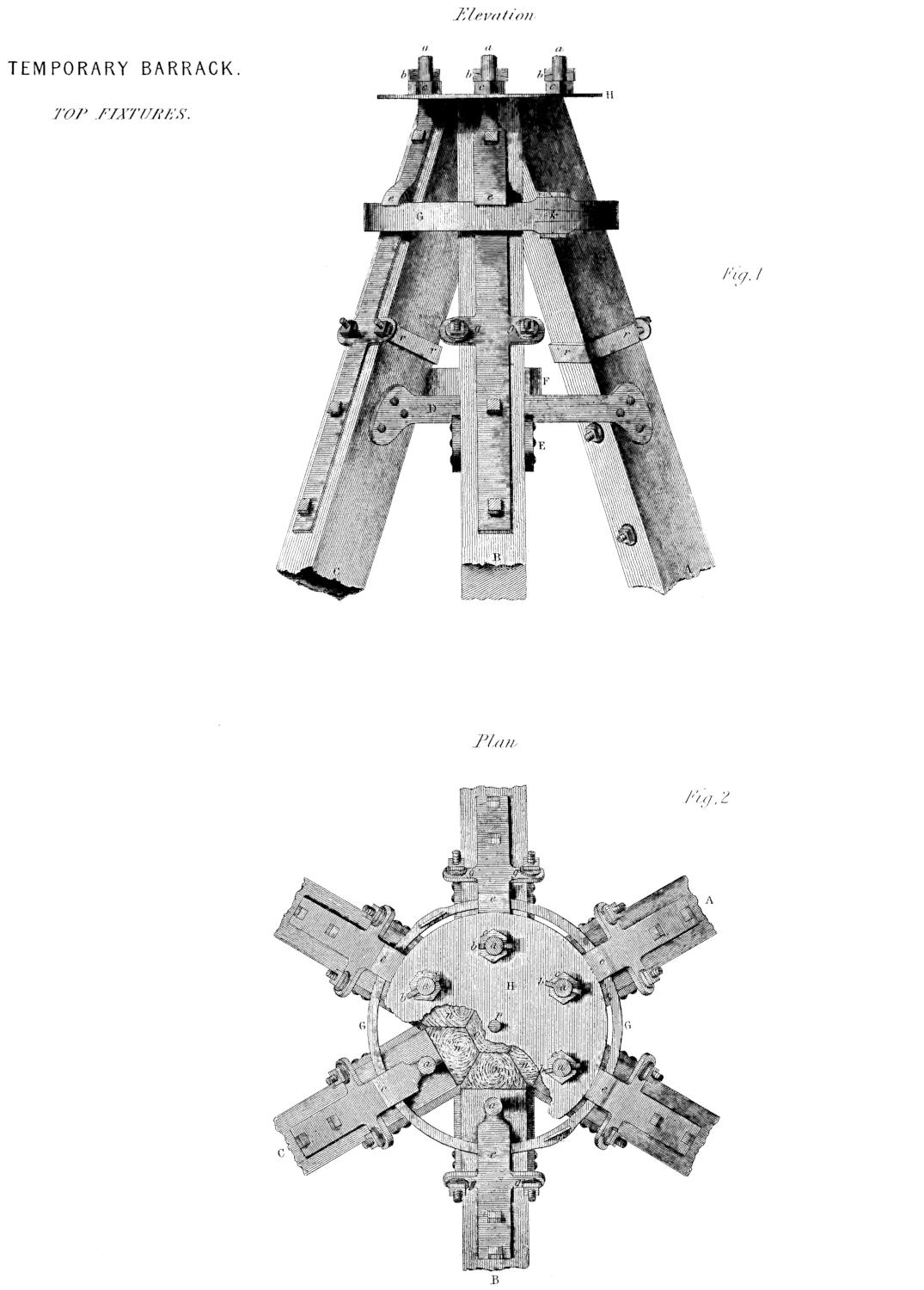
Walter Ferrier Delt. G. Aikman Scuplt.
Elevation
Fig. 1
TEMPORARY BARRACK.
TOP FIXTURES.
Plan
Fig. 2
PLATE VII.
Stevenson’s Account of Skerryvore Lighthouse.

James Andrews, Delt. William Miller, Sculpt.
ELEVATION.
PLATE VIII.
Stevenson’s Account of Skerryvore Lighthouse.
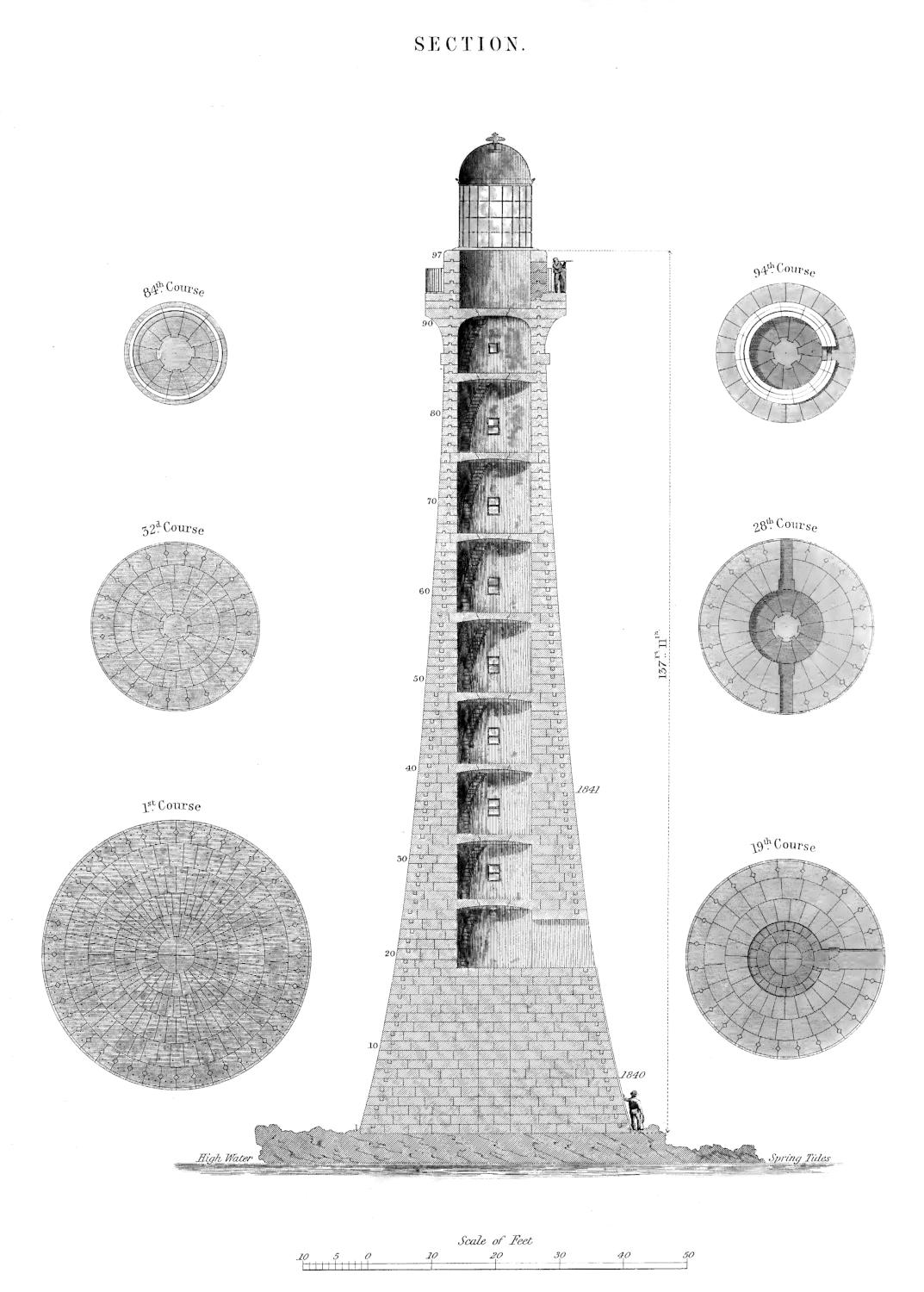
James Andrews, Delt. William Miller, Sculpt.
SECTION.
84th. Course 94th. Course
32d. Course 28th. Course
1st. Course 19th. Course
PLATE IX.
Stevenson’s Account of Skerryvore Lighthouse.
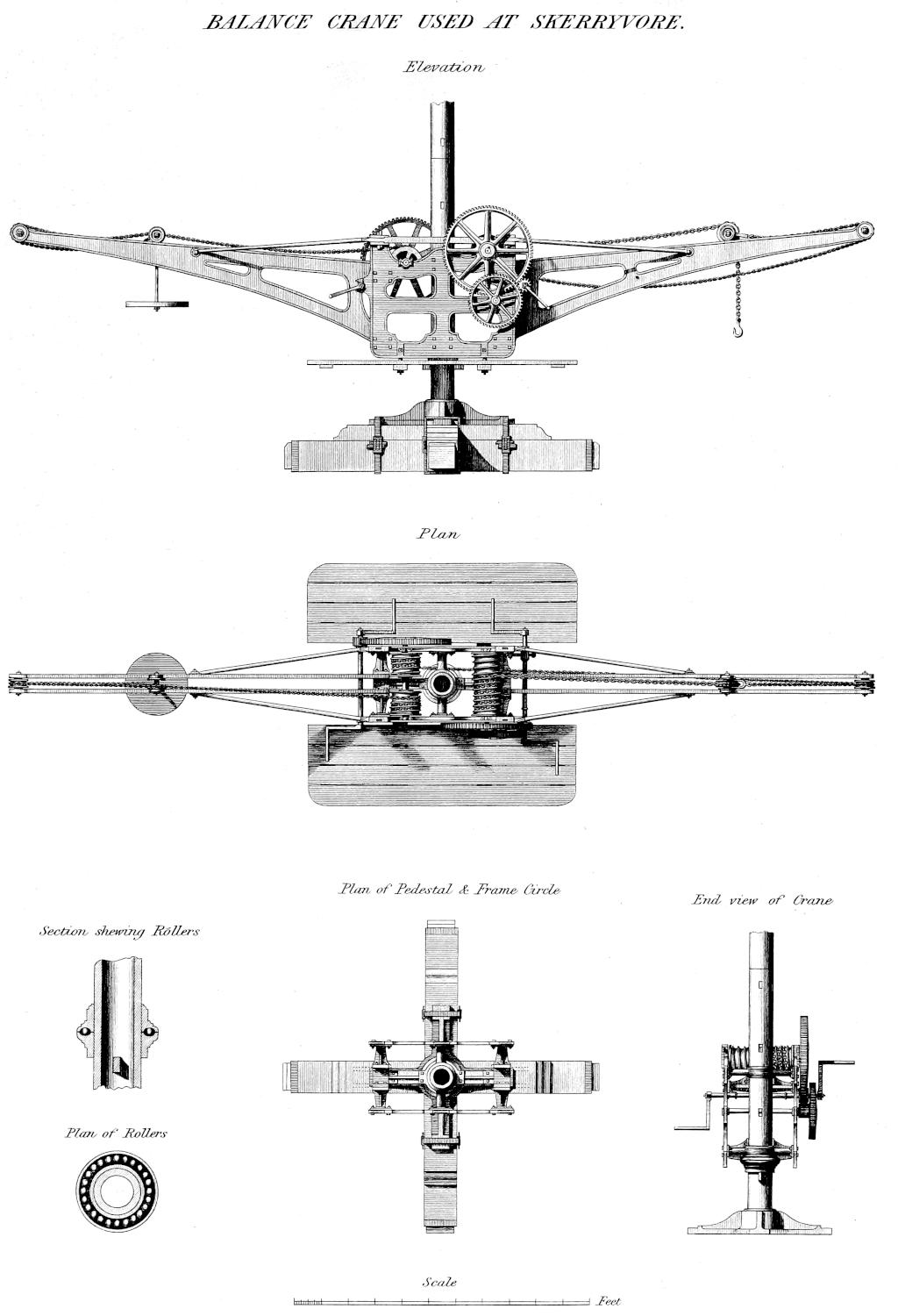
G. H. Slight Delt. W. H. Lizars Sculpt.
BALANCE CRANE USED AT SKERRYVORE.
Elevation
Plan
Section shewing Rollers
Plan of Rollers
Plan of Pedestal & Frame Circle
End view of Crane
PLATE X.
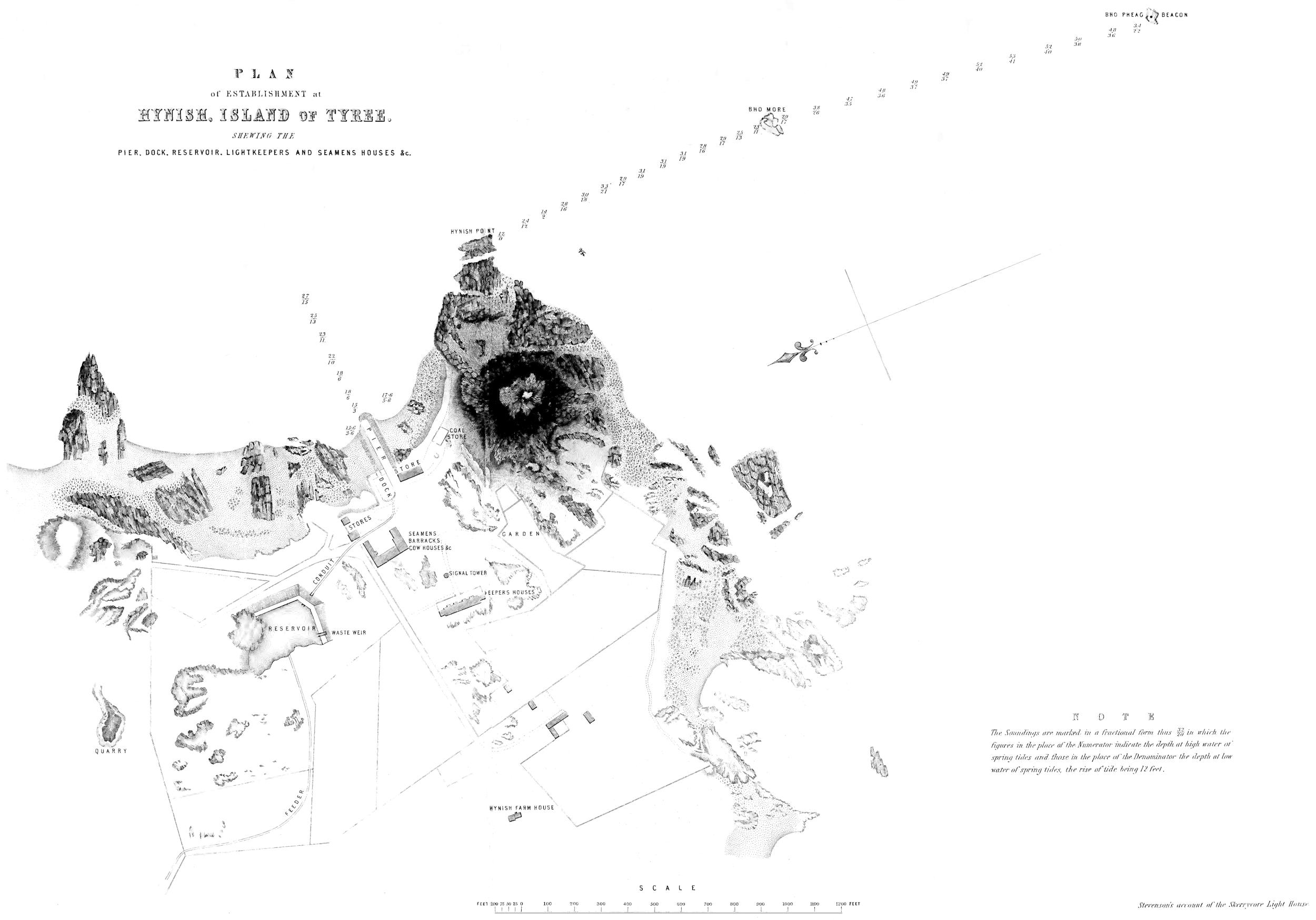
Engraved by W. & A. K. Johnston, Edinburgh.
PLAN
of ESTABLISHMENT at
HYNISH, ISLAND OF TYREE.
SHEWING THE
PIER, DOCK, RESERVOIR, LIGHTKEEPERS AND SEAMENS HOUSES &c.
NOTE
The Soundings are marked in a fractional form thus ³²⁄₂₀ in which the figures in the place of the Numerator indicate the depth at high water of spring tides and those in the place of the Denominator the depth at low water of spring tides, the rise of tide being 12 feet.
Stevensons account of the Skerryvore Light House
PLATE XI.
Stevenson’s Account of Skerryvore Lighthouse.
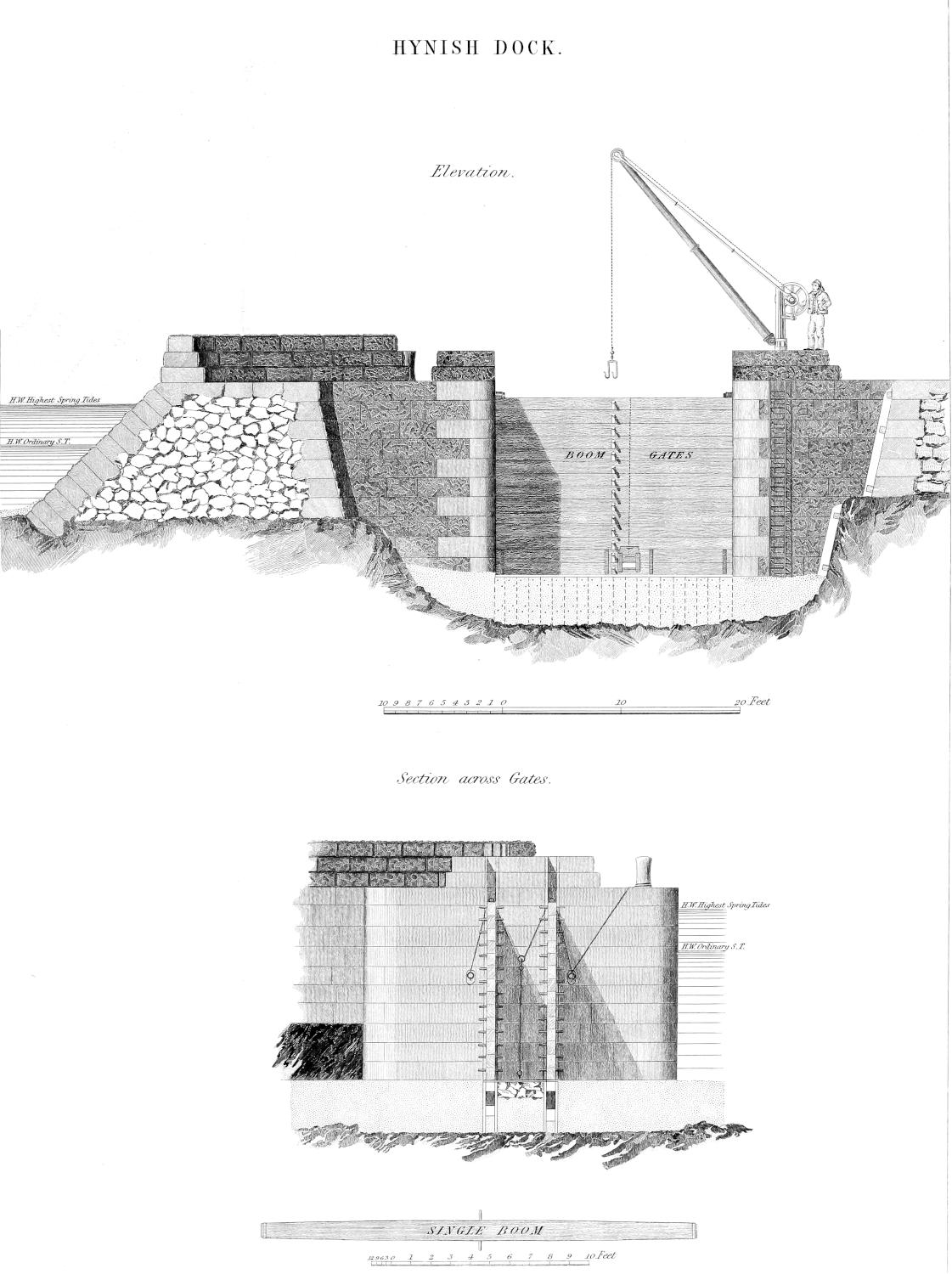
Walter Ferrier, Delt. William Miller, Sculpt.
HYNISH DOCK.
Elevation.
Section across Gates.
SINGLE BOOM
PLATE XII
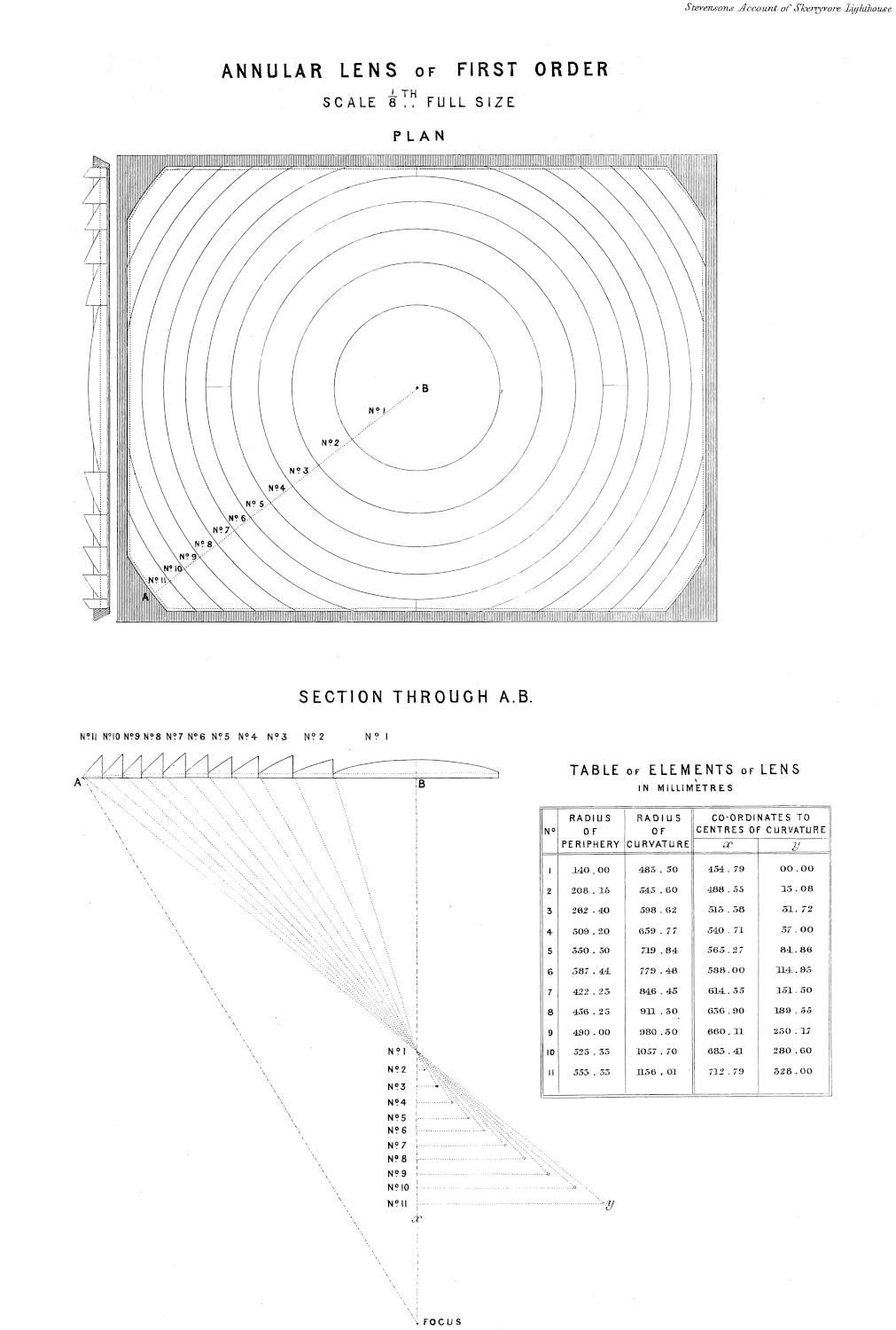
J. L. Kerr, delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
ANNULAR LENS OF FIRST ORDER
SCALE 1¹⁄₈th.. FULL SIZE
PLAN
SECTION THROUGH A.B.
TABLE OF ELEMENTS OF LENS
IN MILLIMÈTRES
| No | RADIUS OF PERIPHERY |
RADIUS OF CURVATURE |
CO-ORDINATES TO CENTRES OF CURVATURE |
|
|---|---|---|---|---|
| x | y | |||
| 1 | 140.00 | 483.50 | 454.79 | 00.00 |
| 2 | 208.15 | 543.60 | 488.55 | 13.08 |
| 3 | 262.40 | 598.62 | 513.38 | 31.72 |
| 4 | 309.20 | 659.77 | 540.71 | 57.00 |
| 5 | 350.50 | 719.84 | 565.27 | 84.86 |
| 6 | 387.44 | 779.48 | 588.00 | 114.93 |
| 7 | 422.23 | 846.45 | 614.35 | 151.50 |
| 8 | 456.23 | 911.30 | 636.90 | 189.55 |
| 9 | 490.00 | 980.30 | 660.11 | 250.17 |
| 10 | 523.33 | 1057.70 | 683.41 | 280.60 |
| 11 | 553.33 | 1136.01 | 712.79 | 328.00 |
PLATE XIII

G. H. Slight Delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
REVOLVING
DIOPTRIC APPARATUS
FIRST ORDER.
ONE TWENTIETH OF FULL SIZE.
PLATE XIV.
Stevenson’s Account of Skerryvore Lighthouse.
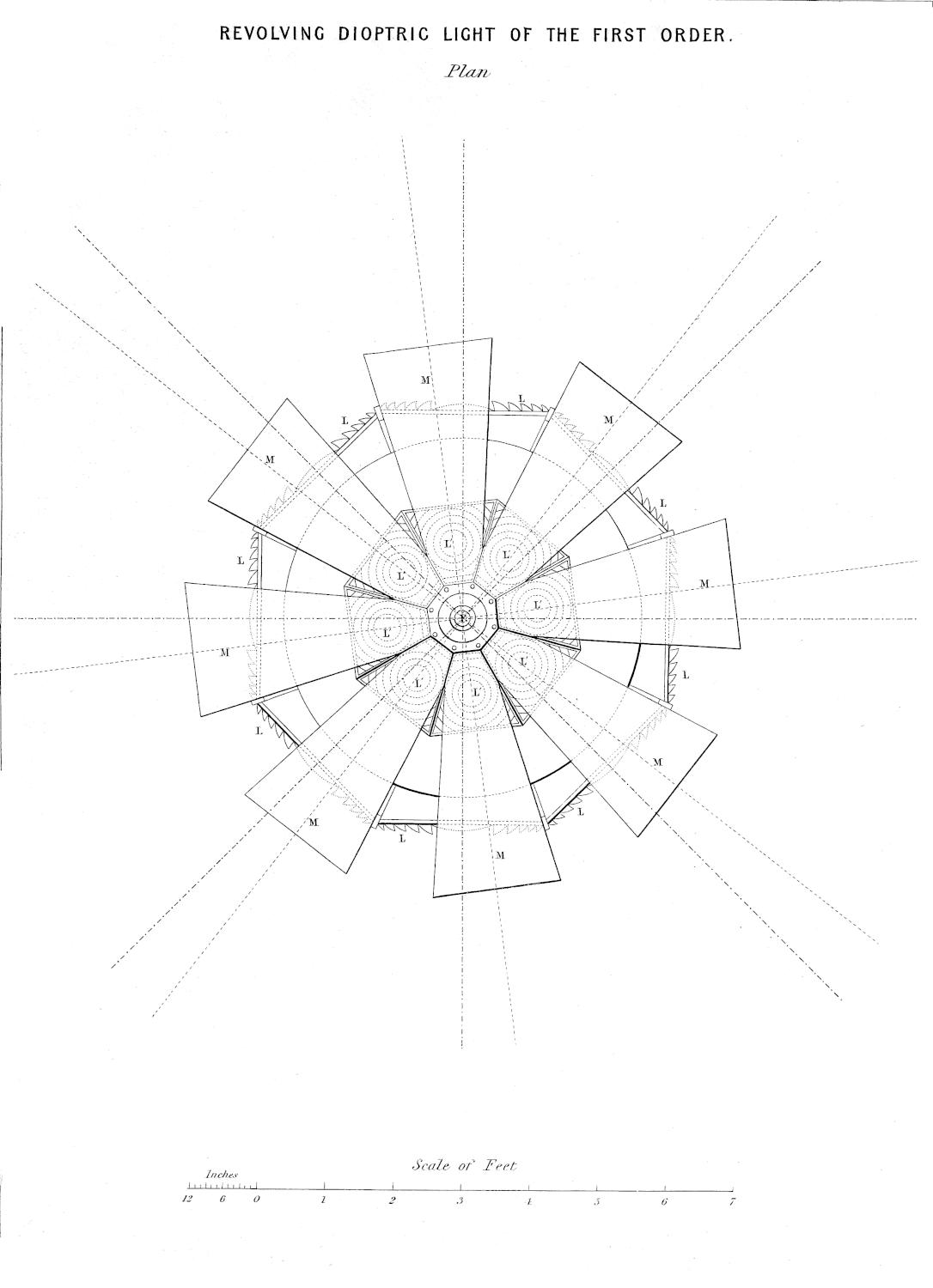
G. Aikman, Sculpt.
REVOLVING DIOPTRIC LIGHT OF THE FIRST ORDER.
Plan
PLATE XV.
Stevenson’s Account of Skerryvore Lighthouse.
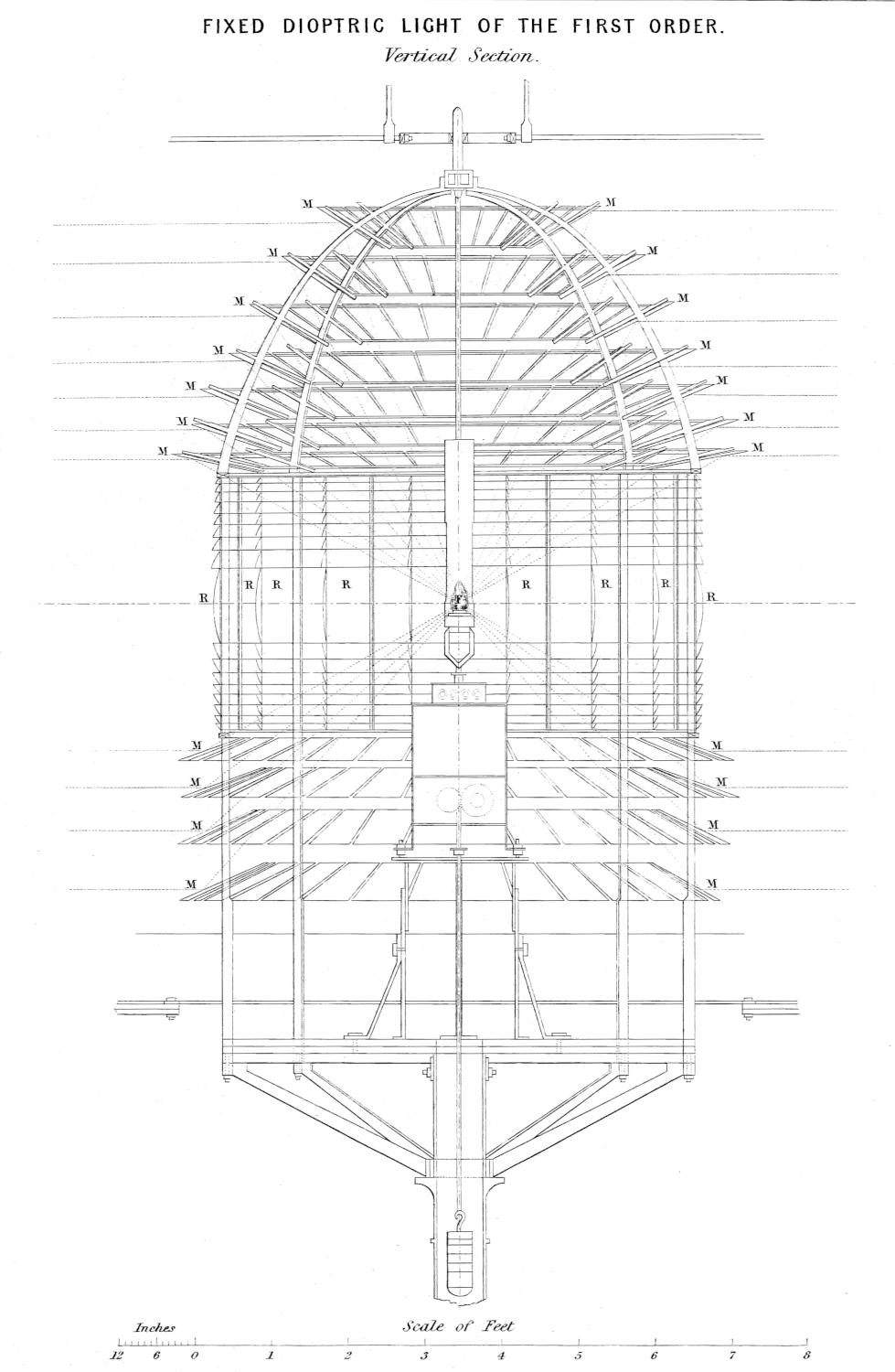
G. Aikman, Sculpt.
FIXED DIOPTRIC LIGHT OF THE FIRST ORDER.
Vertical Section.
PLATE. XVI.
Stevenson’s Account of Skerryvore Lighthouse.
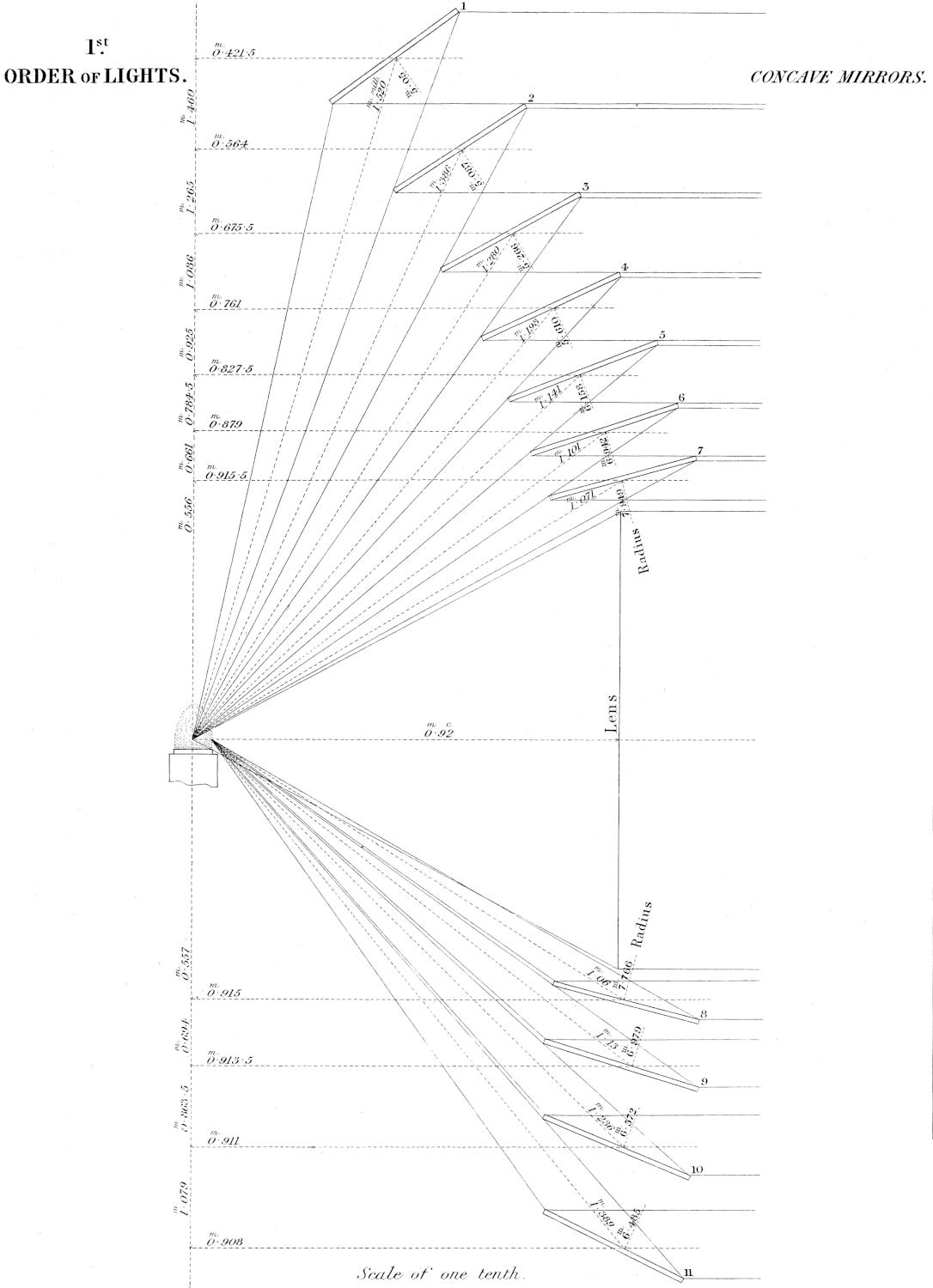
J. Andrews Delt. W. H. Lizars Sculpt.
1st.
ORDER of LIGHTS.
CONCAVE MIRRORS.
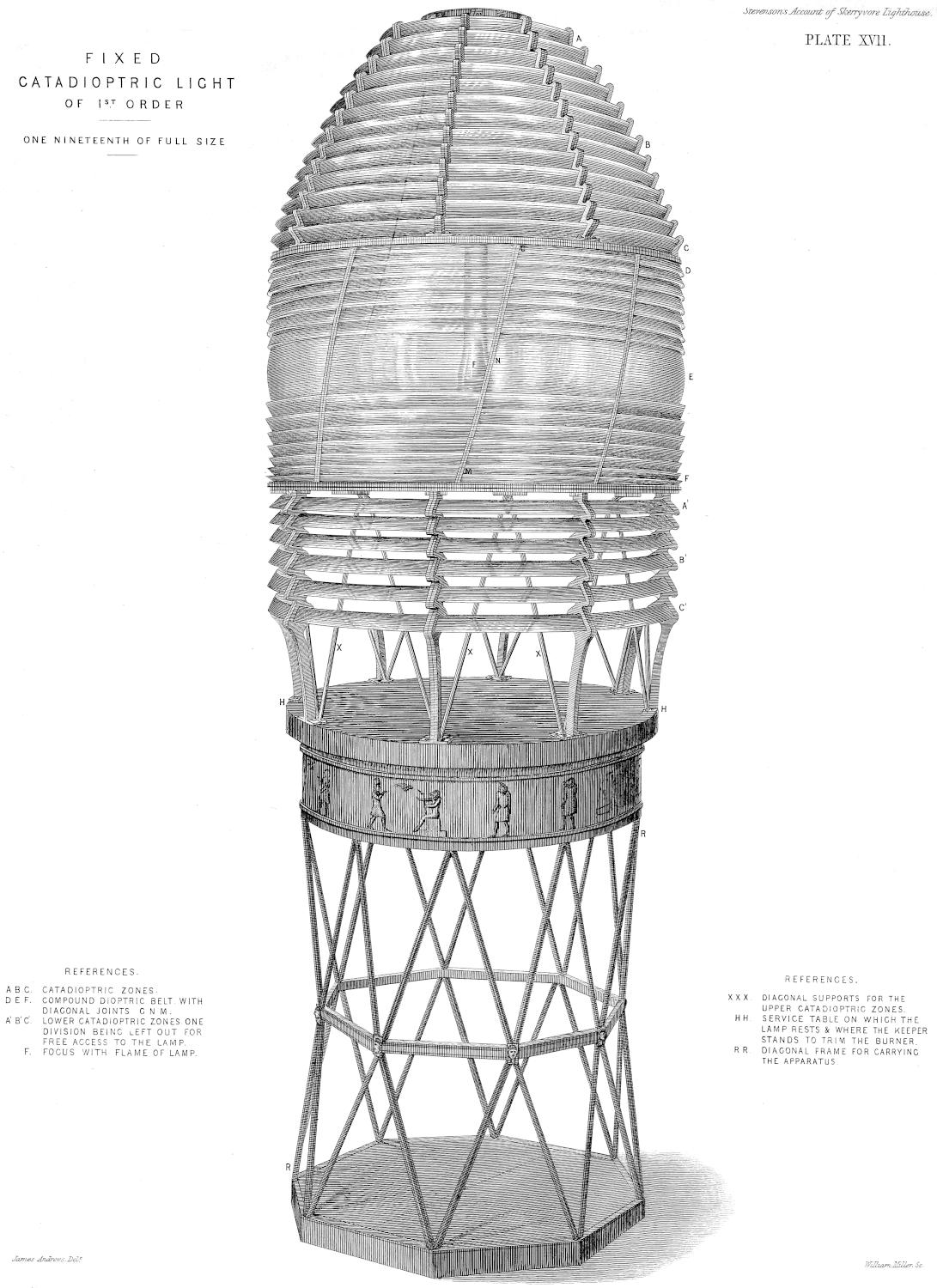
Stevenson’s Account of Skerryvore Lighthouse.
FIXED
CATADIOPTRIC LIGHT
OF 1st. ORDER
ONE NINETEENTH OF FULL SIZE
PLATE XVII.
REFERENCES.
A B C. CATADIOPTRIC ZONES.
D E F. COMPOUND DIOPTRIC BELT WITH
DIAGONAL JOINTS C N M.
A′ B′ C′. LOWER CATADIOPTRIC ZONES ONE
DIVISION BEING LEFT OUT FOR
FREE ACCESS TO THE LAMP.
F. FOCUS WITH FLAME OF LAMP.
REFERENCES.
X X X. DIAGONAL SUPPORTS FOR THE
UPPER CATADIOPTRIC ZONES.
H H. SERVICE TABLE ON WHICH THE
LAMP RESTS & WHERE THE KEEPER
STANDS TO TRIM THE BURNER.
R R. DIAGONAL FRAME FOR CARRYING
THE APPARATUS.
James Andrews, Delt. William Miller, Sc.
PLATE XVIII.
Stevenson’s Account of Skerryvore Lighthouse.
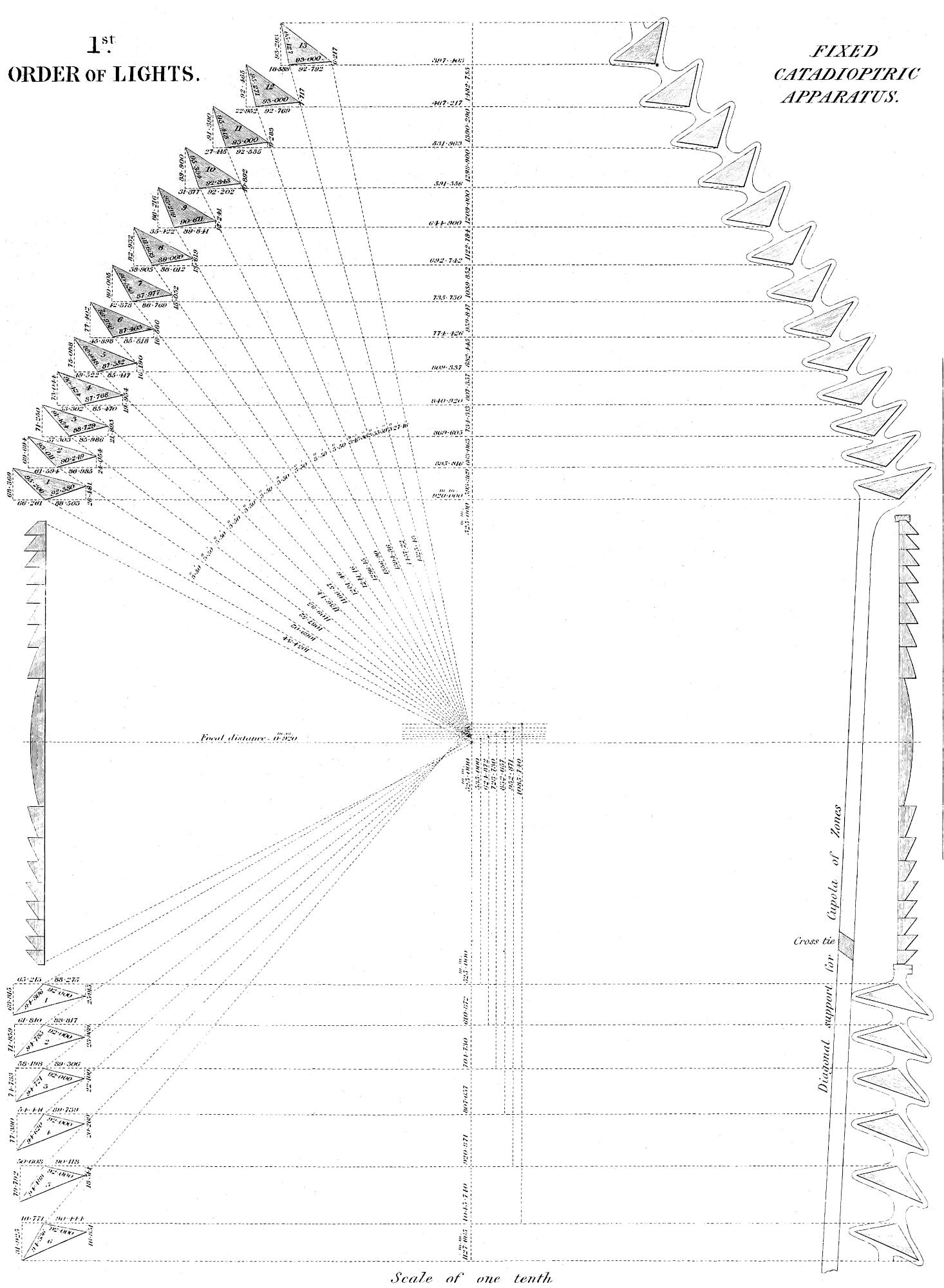
G. H. Slight Delt. W. H. Lizars Sculpt.
1st.
ORDER of LIGHTS.
FIXED
CATADIOPTRIC
APPARATUS.
PLATE XIX.
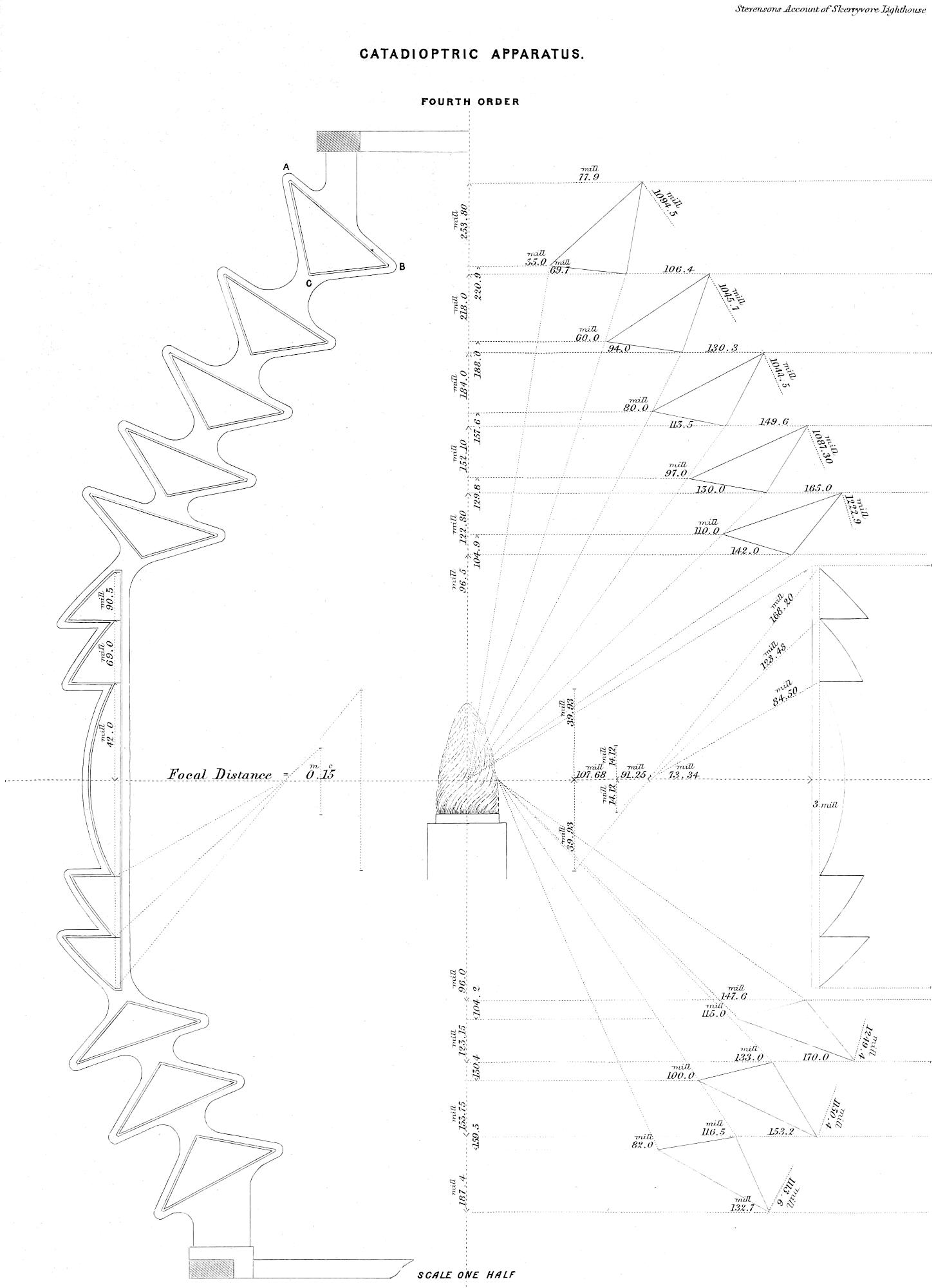
Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
CATADIOPTRIC APPARATUS.
FOURTH ORDER
PLATE XX

Walter H. Ferrier, delt. Engraved by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
MECHANICAL LAMP
for
DIOPTRIC LIGHTS
of
FIRST ORDER.
A WICK HOLDERS
B GLASS HOLDER
C SCREW TO RACK D FOR RAISING WICK
D RACK FOR Do.
E PIPE SUPPLYING OIL TO WICKS
F COLLAR SUPPORTING BURNERS
G DRIP CUP
H RETURN PIPE FOR OIL OVERFLOWING BURNER
I VALVE BOX
J CRANK RODS FOR WORKING LEATHER VALVES
K HINGE OF LID
L LID OF CISTERN
M OIL CISTERN
N SUCTION PIPE
O WINDING ARBOUR FOR MACHINE
P BOX FOR MACHINERY
Q SCREW FOR ADJUSTING LEVEL OF BURNER
R SERVICE TABLE
S COUPLING SCREW FOR OIL TUBE
T UNIVERSAL JOINTS FOR CONNECTING ROD
U CRANE FOR EMPTYING CISTERN
V CONNECTING ROD FOR CRANKS
PLATE XXI

Walter H. Ferrier, delt. Engraved by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
MECHANICAL LAMP.
ENLARGED VIEWS
OF OIL PUMPS.
ELEVATION
J SUPPORTS OF BURNER
P CRANK RODS FOR LEATHER VALVES
M N SUPPORTS FOR CRANK RODS
L COUPLING
T UNIVERSAL JOINT
P CONNECTING ROD FOR CRANKS
S SUCTION PIPE
O SQUARE TRAY FOR OVERFLOWING OIL
Q LID OF OIL CISTERN
I OIL TUBE
PLANS AND SECTIONS IN REFERENCE TO OPPOSITE PLATE.
SECTION ON LINE A. B.
SECTION OF DISCHARGING CHEST E.
PLAN OF VALVES AT F. F. AND H. H.
PLAN AND SECTION OF PLATE K.
PLAN OF UPPER SIDE OF PUMP CHAMBER AT F. F.
SECTION ON LINE C. D.
PLAN OF LOWER SIDE OF PUMP CHAMBER AT H. H.
PLATE XXII
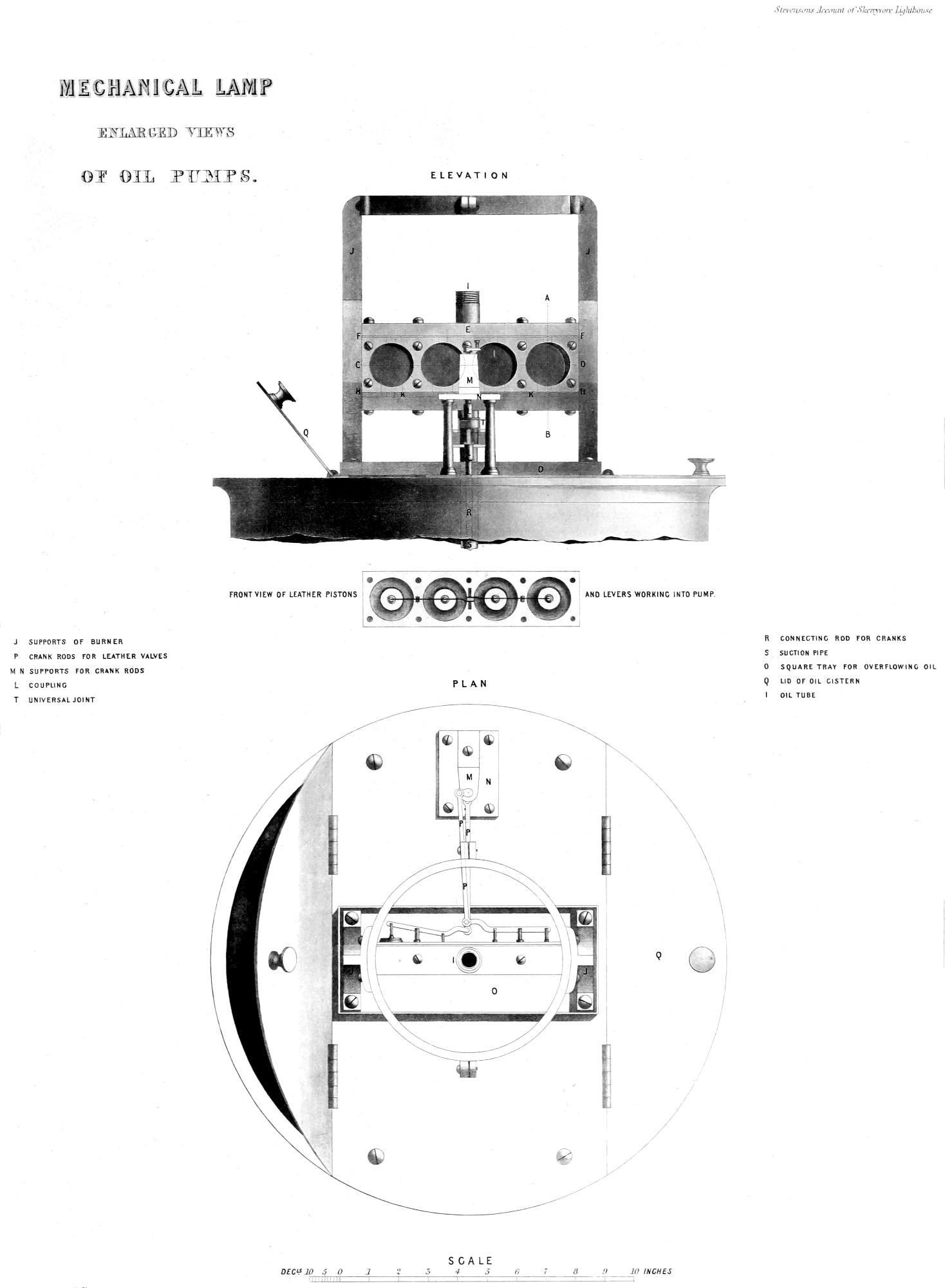
Walter H. Ferrier, delt. Engraved by W. & A. K. Johnston, Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
MECHANICAL LAMP
ENLARGED VIEWS
OF OIL PUMPS.
ELEVATION
FRONT VIEW OF LEATHER PISTONS AND LEVERS WORKING INTO PUMP
J SUPPORTS OF BURNER
P CRANK RODS FOR LEATHER VALVES
M N SUPPORTS FOR CRANK RODS
L COUPLING
T UNIVERSAL JOINT
R CONNECTING ROD FOR CRANKS
S SUCTION PIPE
O SQUARE TRAY FOR OVERFLOWING OIL
Q LID OF OIL CISTERN
I OIL TUBE
PLAN
PLATE XXIII

Walter H. Ferrier Delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
CLOCKWORK MOVEMENT OF MECHANICAL LAMP
PLAN OF CLOCKWORK
SIDE VIEW OF CLOCKWORK
PLATE XXIV
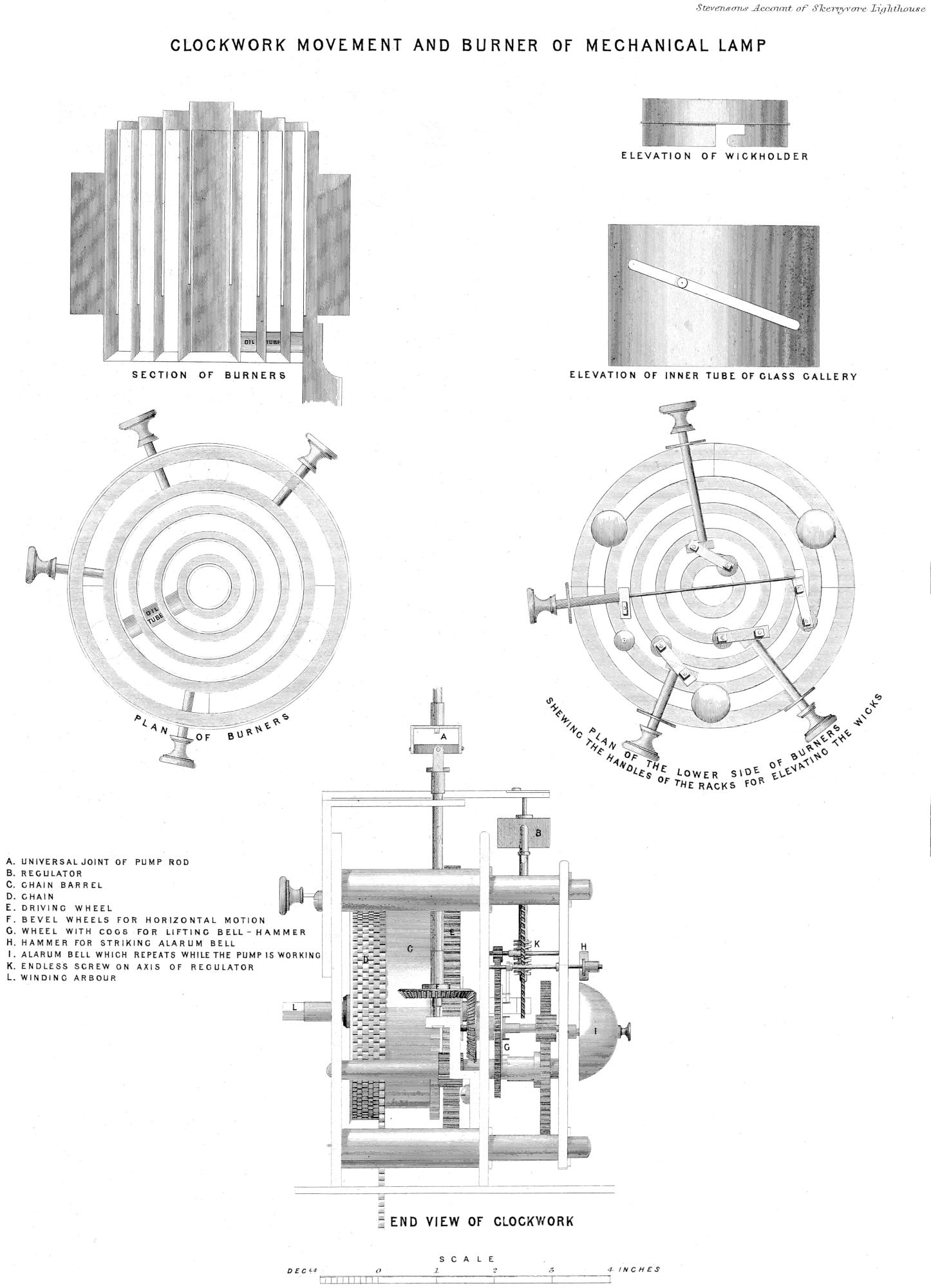
James Andrews, delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
CLOCKWORK MOVEMENT AND BURNER OF MECHANICAL LAMP
SECTION OF BURNERS
ELEVATION OF WICKHOLDER
ELEVATION OF INNER TUBE OF GLASS GALLERY
PLAN OF BURNERS
PLAN OF THE LOWER SIDE OF BURNERS SHEWING THE HANDLES OF THE RACKS FOR ELEVATING THE WICKS
A. UNIVERSAL JOINT OF PUMP ROD
B. REGULATOR
C. CHAIN BARREL
D. CHAIN
E. DRIVING WHEEL
F. BEVEL WHEELS FOR HORIZONTAL MOTION
G. WHEEL WITH COGS FOR LIFTING BELL-HAMMER
H. HAMMER FOR STRIKING ALARUM BELL
I. ALARUM BELL WHICH REPEATS WHILE THE PUMP IS WORKING
K. ENDLESS SCREW ON AXIS OF REGULATOR
L. WINDING ARBOUR
END VIEW OF CLOCKWORK
PLATE XXV.
Stevenson’s Account of Skerryvore Lighthouse.
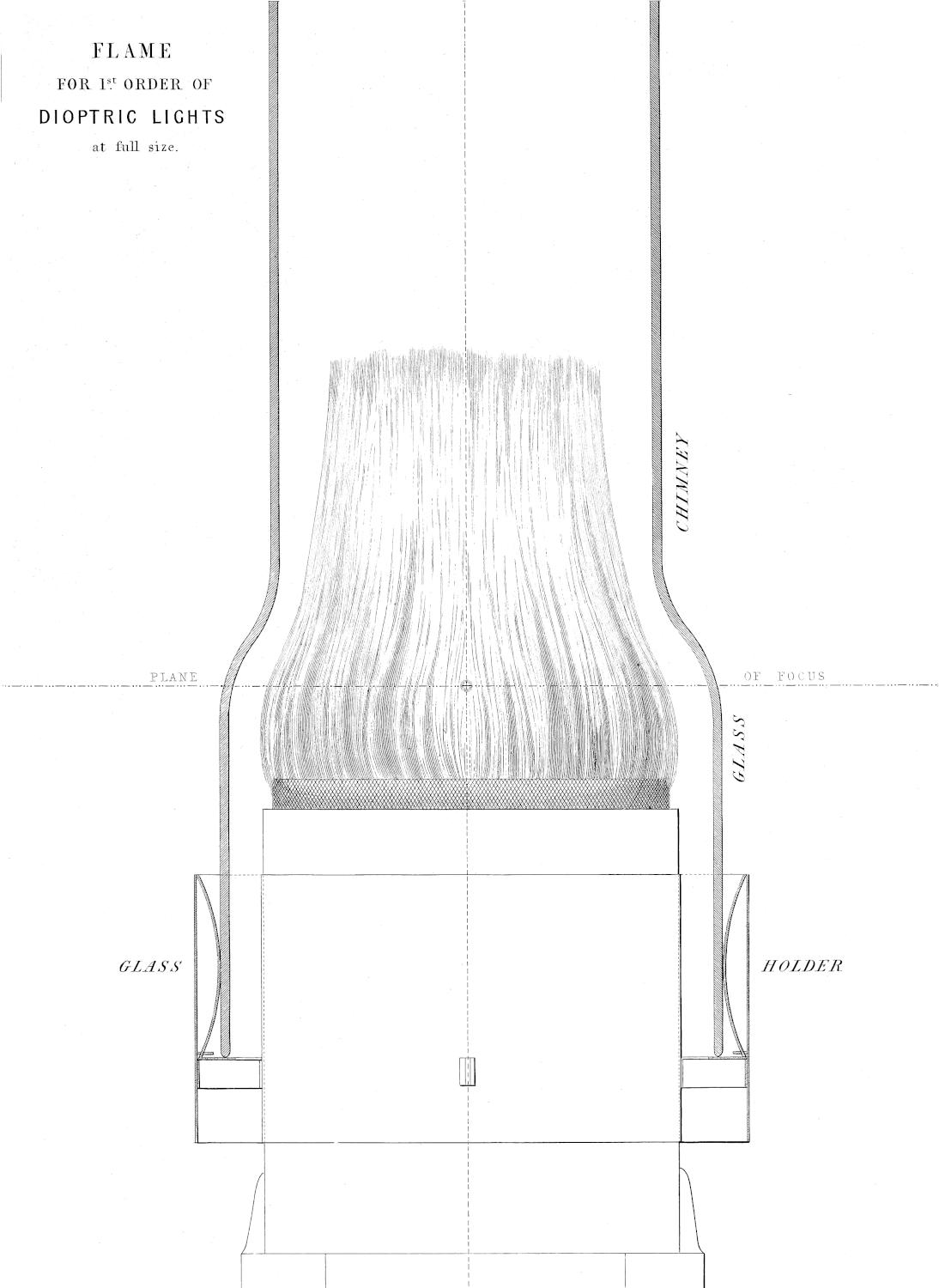
G. Aikman, Sculpt.
FLAME
FOR 1st. ORDER OF
DIOPTRIC LIGHTS
at full size.
GLASS CHIMNEY
PLANE OF FOCUS
GLASS HOLDER
PLATE XXVI
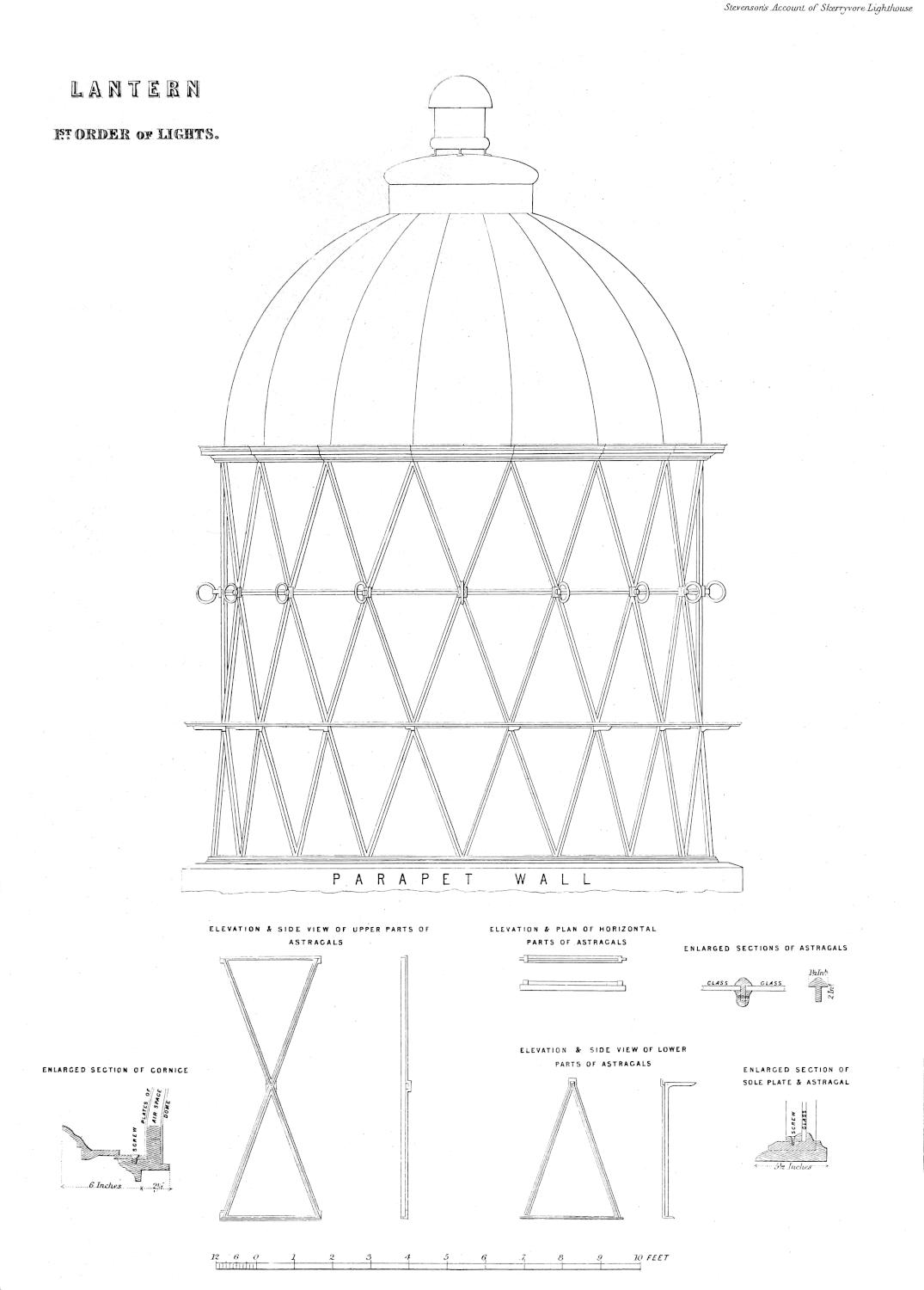
James Andrews Delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
LANTERN
1ST. ORDER OF LIGHTS.
PARAPET WALL
ENLARGED SECTION OF CORNICE
ELEVATION & SIDE VIEW OF UPPER PARTS OF ASTRAGALS
ELEVATION & PLAN OF HORIZONTAL PARTS OF ASTRAGALS
ELEVATION & SIDE VIEW OF LOWER PARTS OF ASTRAGALS
ENLARGED SECTIONS OF ASTRAGALS
ENLARGED SECTION OF SOLE PLATE & ASTRAGAL
PLATE XXVII.
Stevenson’s Account of Skerryvore Lighthouse.

James Andrews, Delt. William Miller, Sculpt.
ARDNAMURCHAN LIGHTHOUSE.
PLATE XXVIII.
Stevenson’s Account of Skerryvore Lighthouse.
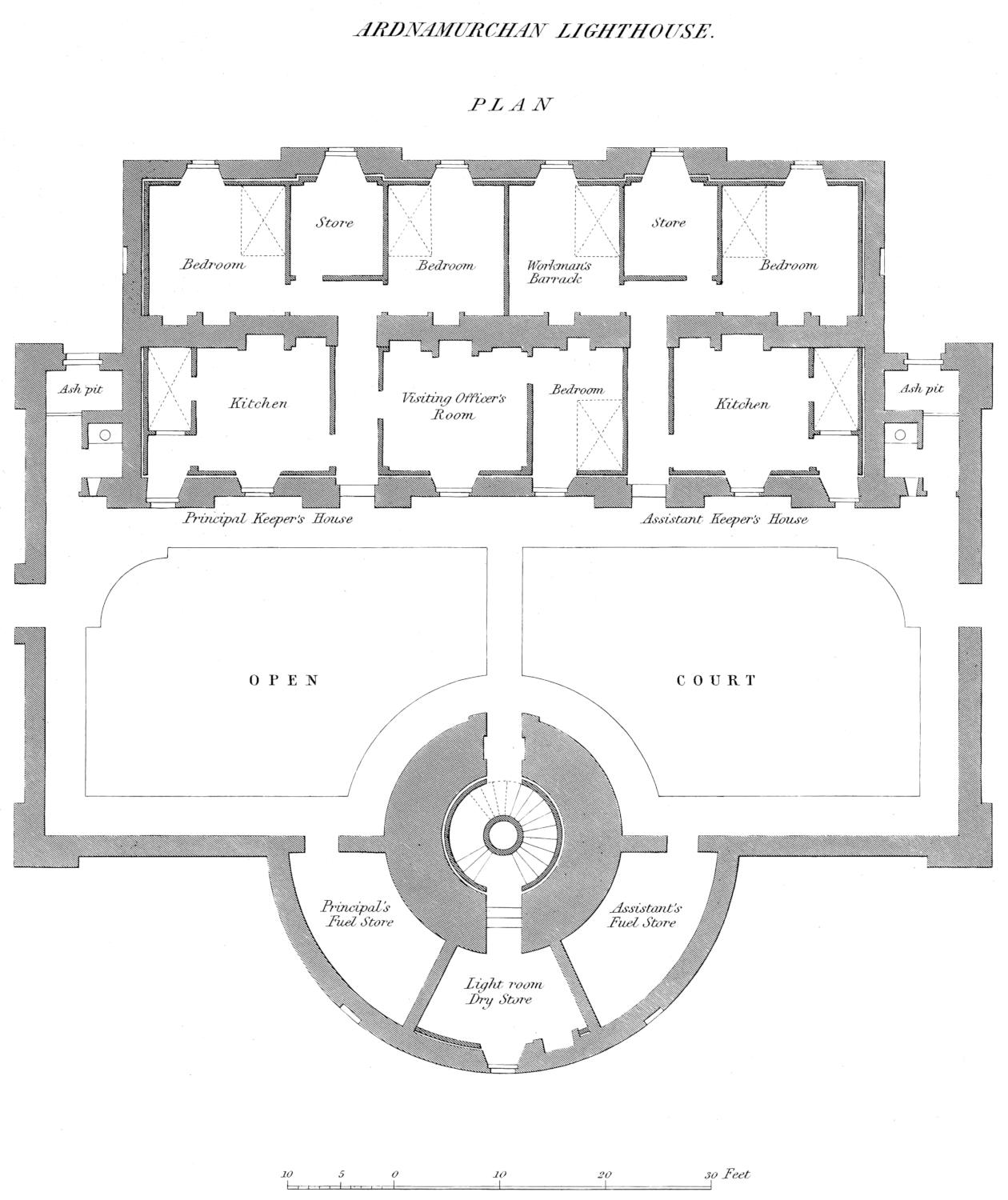
H. G. Slight delt. G. Aikman Sculpt.
ARDNAMURCHAN LIGHTHOUSE.
PLAN
PLATE XXIX
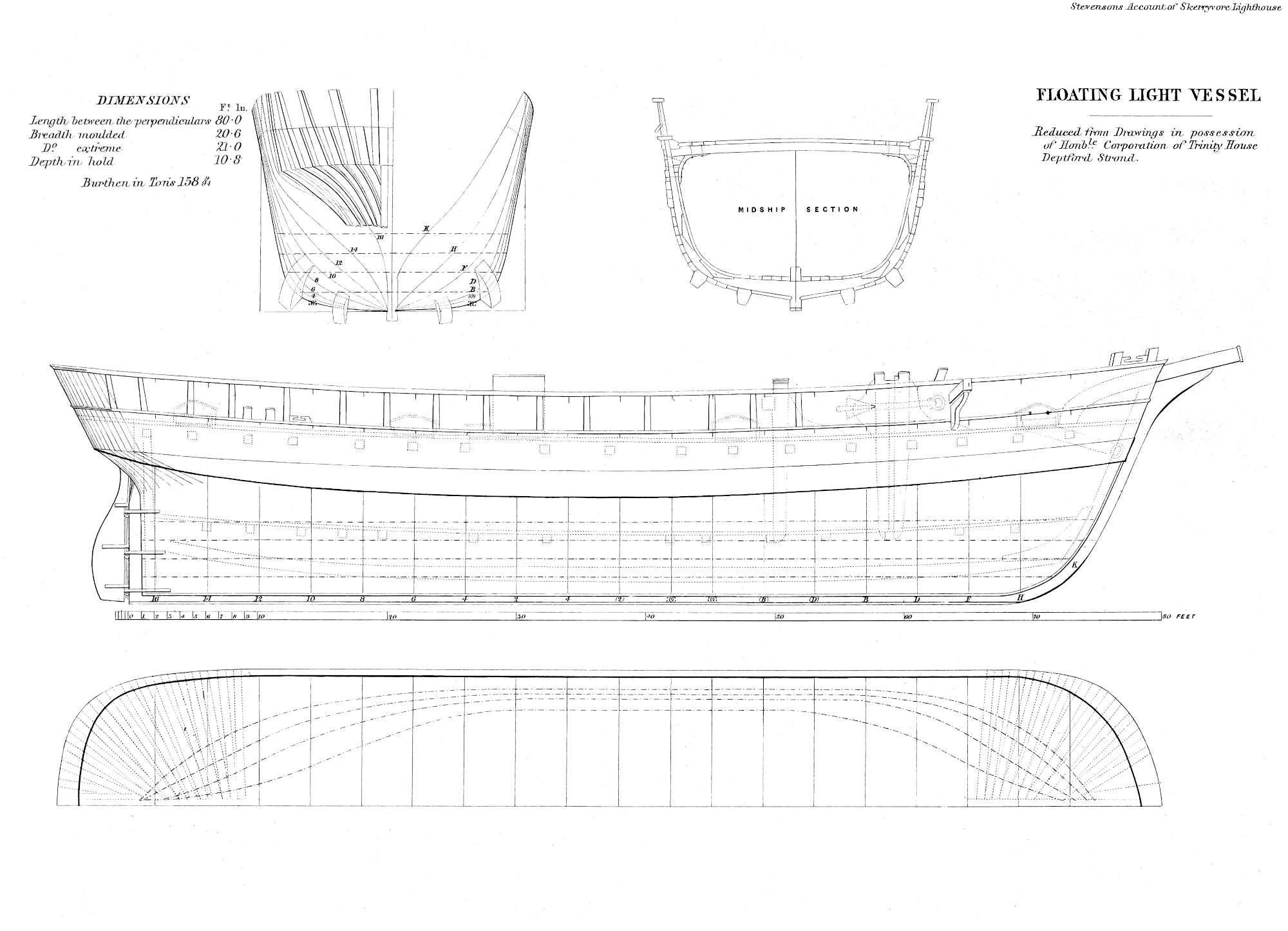
James Andrews Delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
DIMENSIONS
| Ft.In. | |
|---|---|
| Length between the perpendiculars | 80·0 |
| Breadth moulded | 20·6 |
| Do. extreme | 21·0 |
| Depth in hold | 10·8 |
Burthen in Tons 158⁹⁄₉₄
FLOATING LIGHT VESSEL
Reduced from Drawings in possession
of Honble. Corporation of Trinity House
Deptford Strond.
MIDSHIP SECTION
PLATE XXX
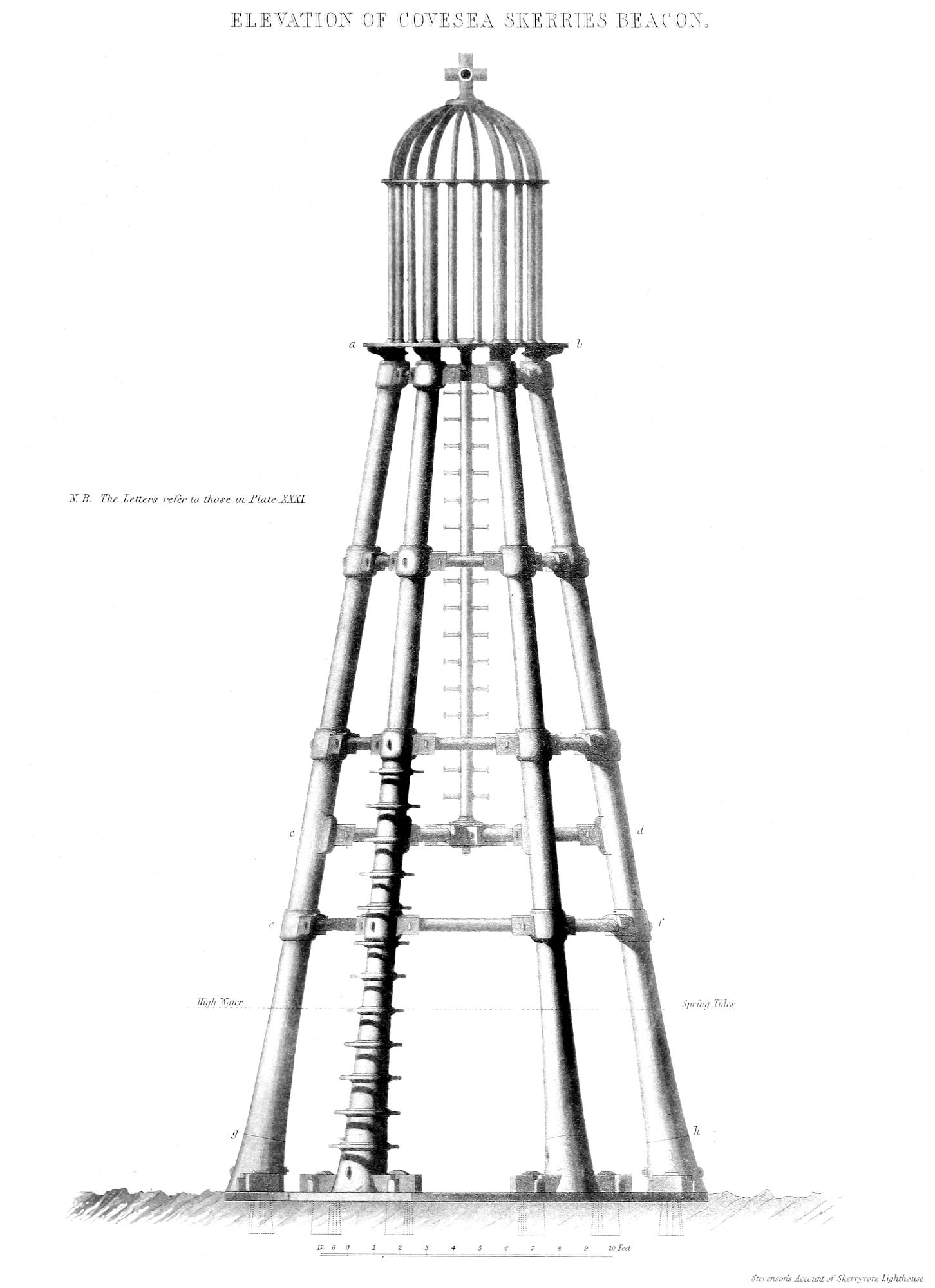
G. H. Slight Delt. Engraved by W. & A. K. Johnston Edinr.
ELEVATION OF COVESEA SKERRIES BEACON.
N. B. The Letters refer to those in Plate XXXI.
Stevenson’s Account of Skerryvore Lighthouse.
PLATE XXXI
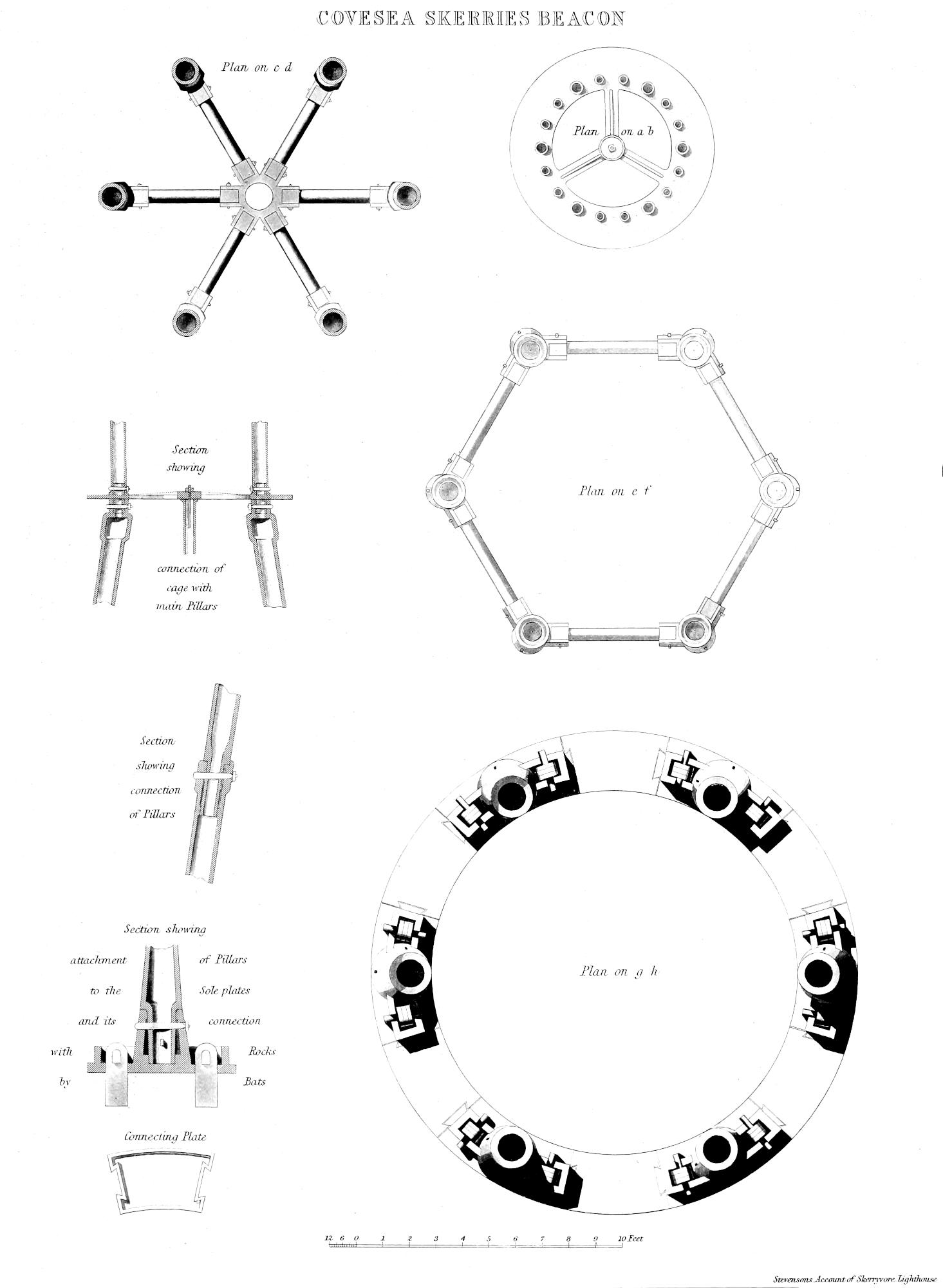
G. H. Slight. Delt. Engraved by W. & A. K. Johnston Edinr.
COVESEA SKERRIES BEACON
Plan on c d
Plan on a b
Section showing connection of cage with main Pillars
Plan on e f
Section showing connection of Pillars
Section showing
attachment of Pillars
to the Sole plates
and its connection
with Rocks
by Bats
Connecting Plate
Plan on g h
Stevenson’s Account of Skerryvore Lighthouse.
PLATE XXXII
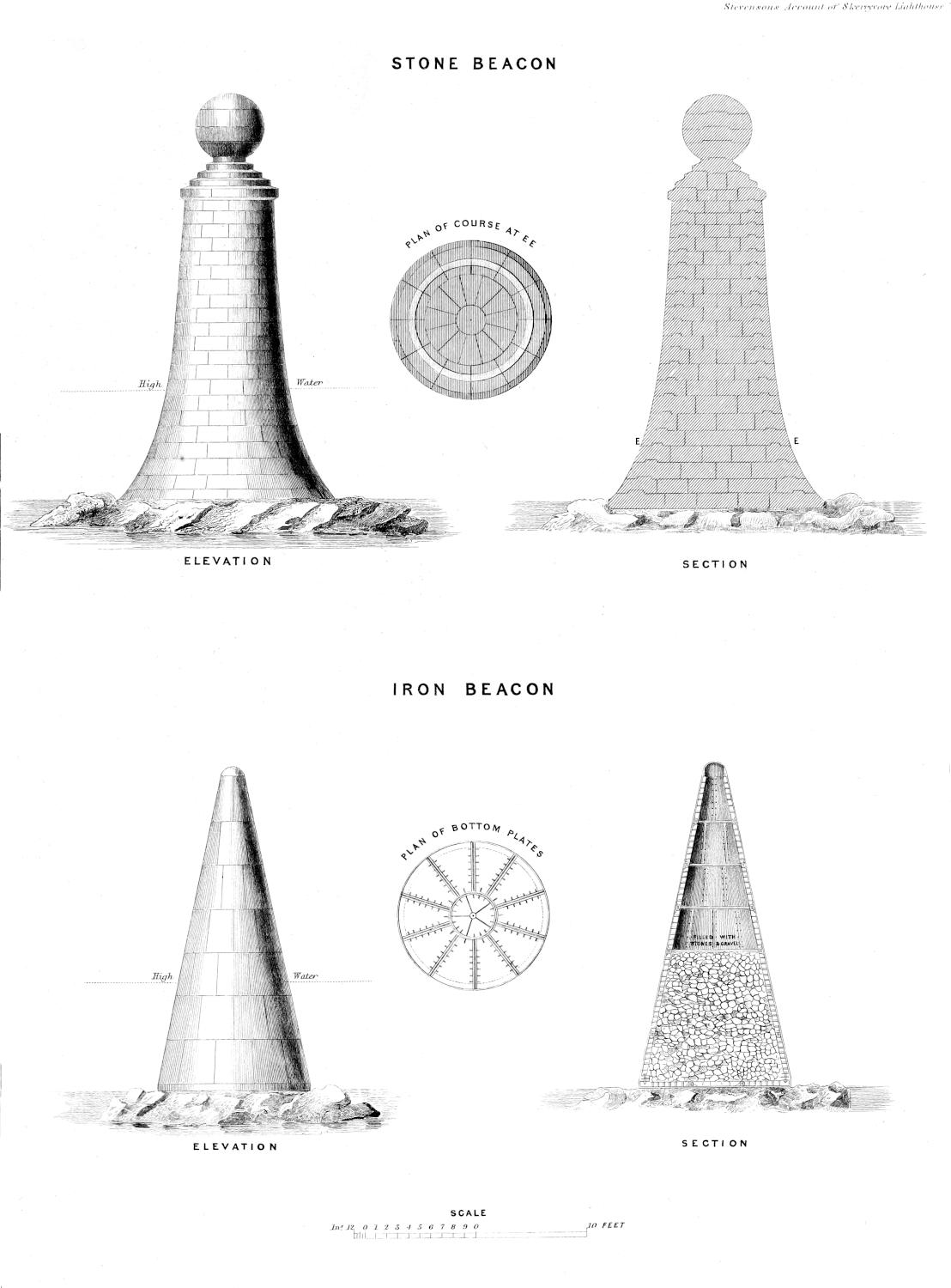
James Andrews Delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse
STONE BEACON
ELEVATION
PLAN OF COURSE AT E E
SECTION
IRON BEACON
ELEVATION
PLAN OF BOTTOM PLATES
SECTION
PLATE XXXIII
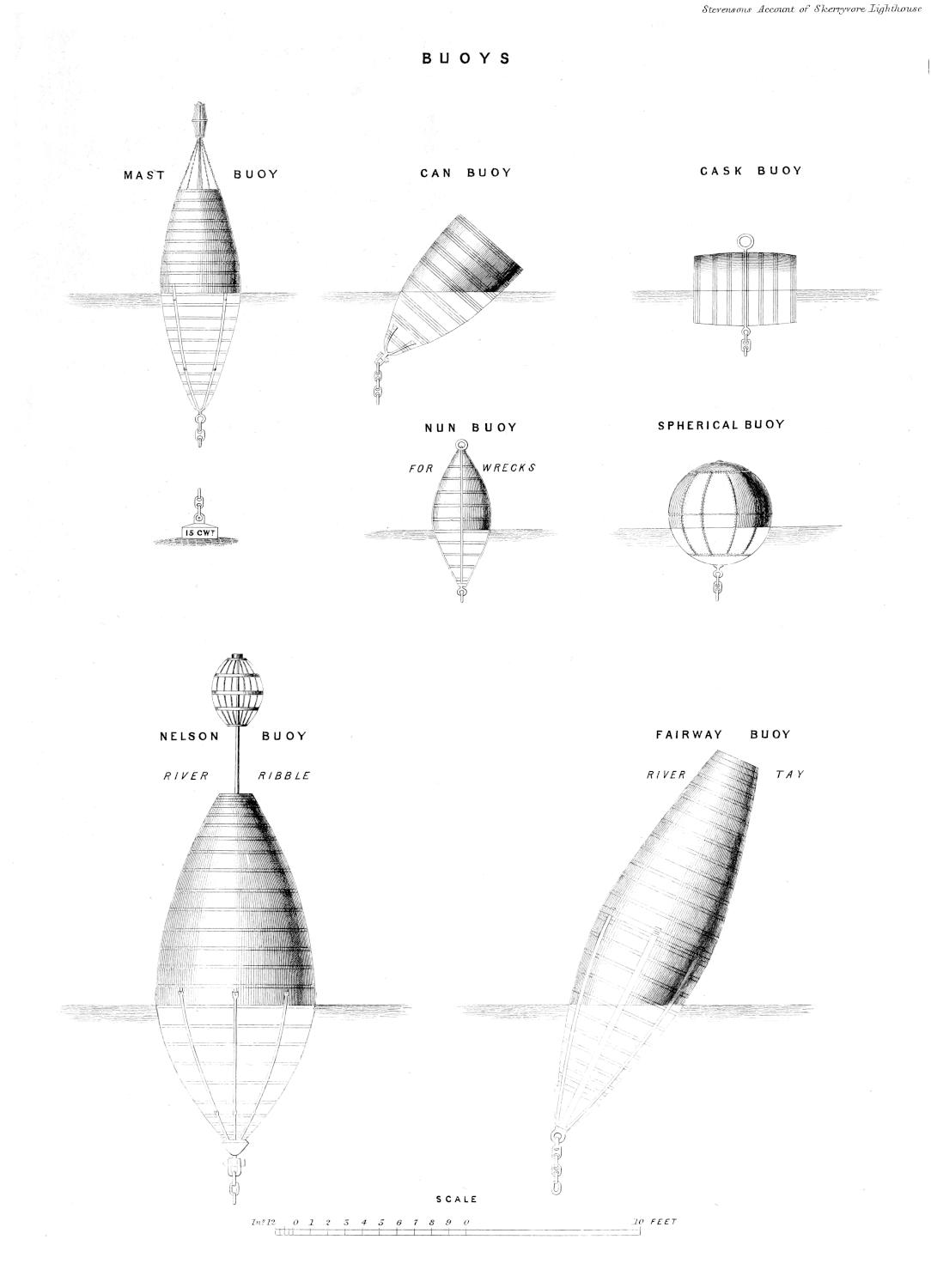
James Andrews Delt. Engd. by W. & A. K. Johnston Edinr.
Stevenson’s Account of Skerryvore Lighthouse.
BUOYS
MAST BUOY
CAN BUOY
NUN BUOY
FOR WRECKS
CASK BUOY
SPHERICAL BUOY
NELSON BUOY
RIVER RIBBLE
FAIRWAY BUOY
RIVER TAY
Inconsistent, archaic spelling, hyphenation, typography etc. have been retained, also in proper and geographic names and in numbering of illustrations and plates, except as listed under Changes below. Depending on the hard- and software used and their settings not all elements may display as intended, and zooming and horizontal and/or vertical scrolling may be necessary to view the larger elements.
The book regularly refers to a book published by the author’s father: An Account of the Bell Rock Light-House by Robert Stevenson, which is available at Project Gutenberg: https://www.gutenberg.org/ebooks/48414.
Text in a dashed box underneath an illustration is text that does not occur as such in the source document, but that has been transcribed from inside the illustration for the sake of clarity.
Page xi: the errata have already been corrected in the text; see also under Changes made below.
Page 149, ... the same mass of Mull stone would weigh 4252 tons ...: possibly an error for 4152 tons (which would make the calculation correct).
Page 174: ... somewhat on the same plan as that which is described in the Appendix ...: it is not clear to which Appendix this refers; possibly the reference is to Plate XXXI.
Page 252 ff.: Figures 59 and 60 are identical.
Page 271 ff.: Figures 71 and 72 are identical.
Page 276, See fig. 73 and the following paragraph: the description appears to refer to Fig. 71/72 rather than to fig. 73.
Page 362, Conversely, n′ is the origin of the co-ordinates for the grinding centre O of the interior convex refracting surface BC, ...: in the illustration (Fig. 110) this appears to be a lower case o.
Page 389, entries for May 14 and 15, 1844: the order as given here is the one printed in the source document; the reason for the inverse order is not clear.
Page 422, item Charities &c, number 2: Since last Act: there appears to be a discrepancy between the individual amounts paid out and the sub-total given.
Changes made:
Footnotes, illustrations and tables have been moved outside text paragraphs; marginalia have been moved to where they appeared to fit best in the paragraph concerned. In certain tables, Do. or do. have been replaced with the dittoed text.
Some obvious minor typographical and punctuation errors have been corrected silently. Some minor oddities in text lay-out have been changed silently for easier readability.
Repeated table and column headers, carry/brought forward, subtotals etc. on page transitions in lists and tables have been removed, except partly on the transition from page 423 to 424.
Suter and Souter have been standardised to Suter.
Page xi: the errata listed have already been corrected in the text. The amount L.93,306 : 8 : 10 does not occur on line 6 of page 178; the amount L.90,268, 12 : 1 that does occur on line 7 of that page has been replaced by L.86,977 : 17 : 7 as given in the Appendix (page 384).
Page 61, Footnote The last column of this table ...: ... will be G·MG·M′, by which expression ... changed to ... will be G·MG′·M′, by which expression ....
Page 231: In these figures, n n shews the reflector flame ... changed to In these figures, n n shews the reflector frame ....
Page 267: François Soliel, whom I urged ... changed to François Soleil, whom I urged ...; ... the light derived from the accessary part ... changed to ... the light derived from the accessory part ....
Page 281: OA = ρ . cos . OAX. changed to OA = ρ . cos OAX.
Page 284: F is the small flame in the focus ... changed to E is the small flame in the focus ....
Page 413, entry The Commission paid to Collectors ...: £2401 : 7 : 0⁴⁄₈ changed to £2401 : 7 : 3⁴⁄₈ cf. page 429.
Page 430, entry 9. Startpoint, Balance: 462 0 8⁶⁄₈ changed to 462 0 3⁶⁄₈.
Page 355: ... forming a flat parallelopepid ... changed to ... forming a flat parallelopiped ....
Page 399, entry Drum Sand West Buoy, South Point: Bear changed to Bearing.